电动汽车双向无线充电器有限集模型预测控制策略研究

胡越 王金明 王天风 梁士福 寇秋林

（1.中国第一汽车股份有限公司研发总院，长春 130013；2.上海万暨电子科技有限公司，上海 201299）

主题词：动力电池-电网互动模式 电动汽车无线充电 双向充电器 模型预测控制

1 前言

近年来，有学者以智能电网技术为背景，提出了车辆到电网（Vehicle to Grid，V2G）的概念[1-2]，配合电动汽车无线充电系统，V2G 可拓展为电池到电网（Batteries to Grid，B2G）[3-4]。B2G 技术中，同时服务于无线充电系统和电网的双向充电器是负责能量转换的核心部件，其性能是决定系统能否实现的重要因素。针对双向充电交流-直流转换器（AC-DC Converter）的控制策略，已有学者取得了大量研究成果[5]。其中，模型预测控制（Model Predictive Control，MPC）系统相比于目前工业界广泛采用的基于比例积分调节器的电网-电压定向直接电流负反馈控制[6]系统，MPC系统在参考信号和反馈信号间出现误差前进行预先计算，而负反馈控制系统在该误差存在后起作用，可见MPC 的动态响应优于反馈控制[7-8]。因此，MPC 更适用于对动态响应有较高要求的双向充电器控制系统。

总体来看，MPC可分为连续控制集与有限控制集2种类型，有限控制集模型预测控制（Finite Control Set MPC，FCSMPC）[9]在电机传动领域也被称为直接模型控制[10]。FCSMPC利用变换器的有限开关状态的离散特性解决实时优化问题，无调制环节，每个控制周期中均对所有开关状态的输出进行评估，在约束条件内选取最优开关状态。文献[11]实现了一种基于FCSMPC 的虚拟同步机，可提升并网设备的电网兼容性。文献[12]针对三电平并网逆变器，提出了一种简化权重系数的FCSMPC，可有效减少控制器计算负担。文献[13]提出了一种改进的FCSMPC方法并应用于风电变流器，基于背靠背试验平台验证了该方法的有效性。文献[14]通过结合FCSMPC与状态观测器减少了传感器的数量，降低了系统成本。FCSMPC 算法利用了电力电子变换器的离散特性，而非受制于该特性，相较于传统控制算法具备响应快速、控制简捷、物理含义明确、便于实现多目标参数优化等特点。

基于FCSMPC的诸多优势，本文建立双向充电器的预测模型，通过仿真验证理论分析的正确性与可行性，并搭建双向充电器试验平台验证该控制策略的完备性与有效性。

2 系统结构与算法描述

电动汽车双向无线充电系统结构及其控制算法如图1所示。其中，常见的DC/DC电源变换器电路由高频逆变器、LCC-LCC补偿网络和高频整流器构成，地面端直流母线通过三相变换器与电网实现连接，ia1、ib1、ic1为充电器侧a、b、c相电流瞬时值，ia2、ib2、ic2为电网侧a、b、c相电流瞬时值，udc为直流侧电压。由于电池电压主要随荷电状态而改变，其变化速度较为缓慢，因而可认为在充电器控制环路的时间尺度（通常为微秒级）下电压不变。uga、ugb、ugc为a、b、c相电网电压瞬时值，ua、ub、uc为a、b、c相各相桥臂的输出电压，uca、ucb、ucc为a、b、c相滤波电容C上的电压瞬时值，L1、L2分别为LCL 滤波器的内、外侧电感。LCL 滤波器能够滤除脉宽调制产生的高频谐波，改善输出电能质量。vinv、vrec分别为逆变与整流电压，Lga、Lva分别为发射线圈和接收线圈的自感，iga、iva分别为发射线圈和接收线圈的谐振电流，谐振补偿网络包括地面端串联电感Lf_ga、地面端串联电容Cf_ga、车载端串联电感Lf_va、车载端串联电容Cf_va。DC/DC电源变换器电路的控制相对简单，双向能量传输仅需改变整流和逆变电压之间的相位角即可，因此本文以较为复杂的双向三相变换器作为研究重点。

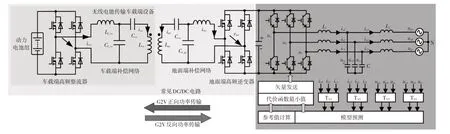
图1 电动汽车双向无线充电充电器系统结构及控制算法示意

根据每一相桥臂上、下管的导通情况，充电器侧可生成8 种电压组合，在传统意义上称为空间电压矢量。本文利用这8种电压矢量构成充电器的有限控制集，如图2所示。

图2 电压矢量构成的双向充电器有限控制集

选取三相静止坐标系到两相静止αβ坐标系的等幅值坐标变换矩阵T为：

则可在αβ坐标系下建立双向充电器的数学模型：

式中，xα为α轴子状态空间，xβ为β轴子状态空间，分别表示为：

将式（3）离散化，可得双向充电器的预测模型为：

式中，k为离散化后的采样序列。

通常，充电器收到的是有功功率指令P*和无功功率指令Q*。当P*<0时，电网向电池侧输送能量进行充电；当P*>0时，电池向电网侧释放能量，协助电网进行削峰填谷。需对指令功率进行换算以得到网侧电流的给定值，便于充电器控制。根据式（5）对有功功率P和无功功率Q进行如下定义：

由式（5）推导可得网侧电流参考值为：

根据稳态条件下正弦电路的相量关系，推导可得电容电压给定值为：

其中，谐振角频率ωres表达式为：

同理可得变换器侧电流给定值为：

为便于在控制集中搜寻最优解，即代价函数最小的解，定义代价函数J：

其中，各分项表达式为：

式中，εi1代表电流i1的控制误差；εi2代表电流i2的控制误差；λi2代表电流误差项εi2的权重系数；λu代表电压误差项εu的权重系数。

最后，将最优矢量发送至各桥臂，通过驱动电路使主电路生成该矢量即可实现充电器的最优控制。即针对控制集中的每个矢量，可预测出k时刻生效的矢量，将第(k+1)个周期电路中的各电压、电流代入代价函数，可以得到8 个代价函数J0～J7的评估值并进行比较，评估值最小的代价函数所对应的矢量即为最优矢量，如图3所示。

图3 有限集模型预测控制的滚动优化过程

当最优矢量为零矢量时，将有2个最优矢量可供选择。此时，以开关状态变化最少为原则进一步进行优选，例如，当前矢量为110时，则选取111为下一周期输出矢量；反之，若当前矢量为001，则选取000 为最优矢量。由此可得算法的整体流程框图如图4所示。

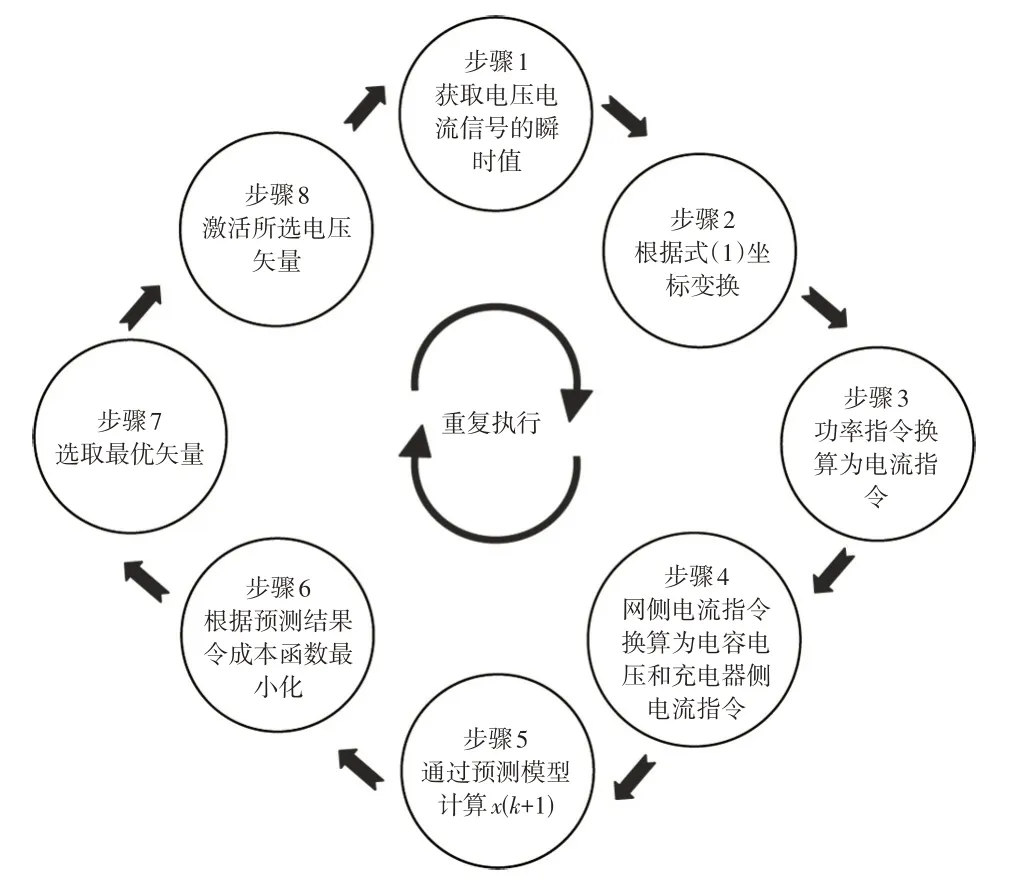
图4 有限集模型预测控制算法流程

3 仿真结果

在MATLAB/Simulink 环境下建立双向充电器仿真模型对并算法加以验证，主要参数如表1 所示，相应的仿真波形如图5～图6所示。

表1 仿真参数设置

图5 系统满载时电网电压和电网电流稳态仿真波形

图6 系统半载时电网电压和电网电流稳态仿真波形

图5 所示为系统满载充、放电时，电网电压和电网电流的稳态仿真波形。由图5可知，基于该算法可以获得较好的稳态控制效果，证明了算法的可行性和有效性。

图6所示为系统半载时，电网电压和电网电流的稳态仿真波形。该仿真波形进一步证明了基于该算法，系统在各种工况下均具有较好的稳态控制性能。

4 试验验证

为进一步验证控制算法的可行性，搭建了额定功率为10 kW的电动汽车无线充电系统整机测试试验平台，如图7 所示。无线传能磁耦合机构放置于六自由度台架，便于调整传输距离；样机交流侧接入三相市电；样机直流侧接入额定功率为18 kW的双向电源，既可充当负载也可充当电源；利用功率分析仪PW60001 测量输入电压、输入电流等数据；设计了UI界面用于监视系统各控制变量。本文所提出的有限集模型预测控制策略集成在WallBox中。

图7 电动汽车无线充电系统整机测试平台

图8所示为功率正向传输的试验波形，即三相变换器工作于电动汽车充电工况。图8展示了功率逐步升高满载的波形，可以看到电压电流同相位，三相电流正弦度高，不仅获得了期望输出功率，也获得了较高的功率因数。

图8 G2V功率传输试验波形

图9所示为功率反向传输时的试验波形，即电动汽车通过三相变换器向电网馈电阶段，可以看到电压电流相位翻转180°，电池为电网提供支撑，实现了较好的并网功能。

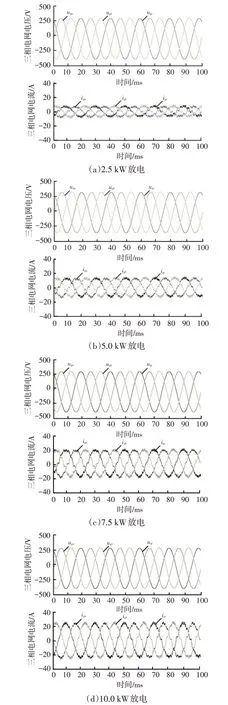
图9 V2G功率传输试验波形

为验证所提出的MPC 算法，图10 给出了10 kW 正向功率传输条件下传统控制算法和MPC 算法的波形图。由图10 可以看出，传统控制算法的三相电流存在部分畸变，输入电流总谐波失真约为7%；MPC算法的三相电流较为接近正弦波形，输入电流总谐波失真约为3%，控制效果得到提升。

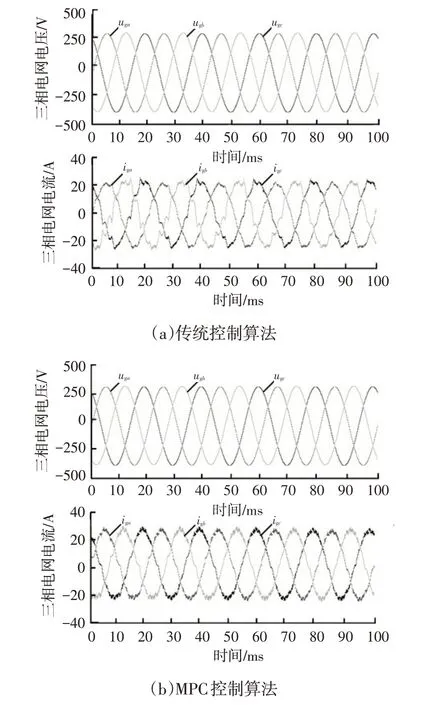
图10 10 kW传输功率条件下不同控制算法性能对比

由图10 可以看出，所提出的有限集模型预测控制策略可成功应用于电动汽车双向无线充电系统，在2.5 kW、5.0 kW、7.5 kW和10 kW功率下成功实现了正、反向功率传输，并且获得了较好的电能质量。

5 结束语

本文针对一种用于电动汽车双向无线充电系统的有限集模型预测控制方法展开研究，利用滚动优化原理，基于预测结果优选最优矢量，通过合理控制开关管导通与关断发送该最优矢量，给出详细算法流程。最后建立了10 kW 功率的仿真模型与试验平台，实现了不同功率等级下的正向和反向功率传输，获得期望的功率和较好正弦度的电流，所得结果验证了算法的正确性与有效性。