海底电缆在涡激振动下的疲劳寿命

程 志,洪爱军,梁 毅,董 红,罗楚军

(1.广东电网有限责任公司 广州供电局,广东 广州 510620;2.中国电力工程顾问集团 中南电力设计院,湖北 武汉 430071)

0 引 言

海底电缆输电工程是跨海域电力联网工程的重要组成部分，已广泛应用于电网跨海域互联、海洋岛屿供电、海上石油平台供电、海上可再生能源发电并网等方面。海底电缆工程普遍造价昂贵、施工抢修极其复杂，一旦发生故障后果严重，因此对海底电缆系统的安全可靠性有很高的要求[1-2]。

由于海底地形、冲刷等原因，难免会出现海底电缆与海床表面不直接接触的悬空段。在一定条件下，水流流经电缆时产生旋涡，并且旋涡以一定的频率在电缆后侧交替释放，使电缆受到顺流向的波动阻力和垂直于流向的波动升力，引起电缆振动。当旋涡脱落的频率接近电缆结构的自振频率时，会发生频率锁定现象，使电缆发生较大的振动，这就是共振现象，共振不会马上对电缆结构产生破坏，但会加剧电缆的疲劳破坏[3]。由电缆频率锁定和振动导致的结构失稳是影响电缆使用寿命、引发悬空段疲劳失效的重要形式[4]。

因此，正确认识海底电缆与洋流的相互运动规律，研究旋涡引发的振动响应，寻求一种切实可行的计算分析方法，评估其对海底电缆寿命的影响，对保证海底电缆的安全运行、有效地指导海底电缆的工程设计和运行维护具有重要的意义。

海底电缆疲劳分析仿真模型是在海底悬跨电缆涡激振动的响应预报模型的基础上，通过计算分析，得到海缆悬空段不同位置处的振动强度；得到悬跨海缆的振动位移之后，可根据梁理论得到海缆各点的弯曲应力及应变；根据海缆各点应变，结合应变疲劳曲线和雨流计数法，计算海缆的应变循环次数和疲劳损伤，再根据Palmgreen-Miner线性损伤累积理论可求得海缆的疲劳寿命[5]。

本文基于洋流作用下海底电缆涡激振动机理，结合VIVANA软件建立海底电缆振动模型，计算分析影响海底电缆疲劳寿命的主要因素，进而根据计算结果对海底电缆的振动防护提出相应措施。

1 仿真模型建立

1.1 海底电缆振动仿真模型

采用柔性梁模拟缆跨结构，结合VIVANA中水动力模型建立悬跨海底电缆涡激振动的数值预报模型[6-7]。结构假设基于小变形、平截面、线弹性，对柔性梁而言，可认为梁的挠曲位移在变形不大时其挠度函数v(x)的导数即为转角，梁上任意一点的位移可表示为相应中轴线的位移，再加上截面绕中轴线转动，这也就是梁的伯努利理论[8]。

该程序的计算过程如下：

(1)采用有限元方法对海缆结构进行离散，整合得到质量矩阵M、阻尼矩阵C、刚度矩阵K，分析结构固有特性，得到结构的主振型及对应频率。

(2)通过迭代得到海缆的可能响应频率，并进行主响应频率判别。

(3)求解海缆的动力平衡方程，得到海缆涡激振动的响应幅值。

(4)预报疲劳损伤，预报过程依赖于海底悬跨海缆涡激振动的响应预报模型，通过计算分析，得到海缆悬空段不同位置处的振动强度，进而得到沿电缆轴向及截面上涡激振动引起的疲劳损伤。

采用VIVANA程序进行计算的主要输入输出参数如图1所示。

1.2 海底电缆动力平衡方程

将缆跨视为柔性梁，采用有限元方法对梁进行离散，计算单元的结构特性矩阵从而集成梁的整体结构特性矩阵，式(1)为有轴向力效应的梁单元动力平衡方程[9]：

(1)

式中：m为单元质量矩阵；c为单元阻尼矩阵；k为弹性刚度矩阵；kG为几何刚度矩阵；v(t)为单元位移矢量；t为时间；p(t)为载荷矢量。

(2)

式中：各项由左往右分别为单元结点的惯性力矢量、阻尼力矢量、弹性力矢量和外载荷矢量。

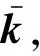
(3)

式中：r(t)为位移矢量列阵；R(t)为载荷矢量列阵。

2 海底电缆疲劳寿命仿真计算方法

2.1 海底电缆应变计算

动力平衡方程是一个矩阵方程，求解动力平衡方程可得到沿海缆长度方向各结点的位移幅值yj，假定每个结点做简谐振动，因而也就得到每个时刻沿缆线不同截面的振动位移y(x，t)[10]。单元结点力计算式为

sj，q=kqyj，q，j=1，2，…，N，

q=1，2，…，Nq

(4)

式中：sj，q为弯矩和剪力组成的单元结点力列阵；kq为单元刚度矩阵；yj，q为yj中与单元自由度分量对应的响应矢量；N为自由度数；Nq为总的单元数；sj，q和yj，q为4×1的列阵；kq为4×4的矩阵。

得到单元结点力列阵之后，经过集成得到沿缆线各结点的弯矩和剪力，电缆横截面上各点的应力计算式为

(5)

式中：x为电缆坐标；yp为电缆横截面上应力计算点距中轴线的距离；I为截面惯性矩；M(x，t)为弯矩。

不考虑电缆结构中不同分层之间的摩擦，应变与应力之间具有如下关系：

(6)

式中：ε为应变，无单位；σ为应力，Pa；E为弹性模量，Pa。电缆各层承受的应变计算式为

(7)

式中：a为振动幅值，m；rd为计算电缆层的半径，m；n为模态数；L为悬跨长度(下文简称“跨长”)，m。

2.2 海底电缆疲劳寿命计算

对于已知某海域流速分布的情况，1 a内(用流速u表示)应变循环次数计算式为

(8)

式中：Na(u)为1 a内在流速u作用下的应变循环次数；T为计算得到的应变时间序列的时间长度(按小时计)；NT为时间T内的应变循环次数，可采用雨流计数法得到，若当海流流速为u时海缆响应频率为f(Hz)，则时间序列T(1 h)内所产生的应变循环次数为3 600f；ta为1 a的小时数，ta=8 760 h；P(u)为流速u对应的概率密度。

关于洋流流速的概率分布P(u)，其表达式为

(9)

式中，α、β和γ分别为尺度参数、形状参数和位置参数。在本计算中取重现期1 a、10 a、100 a对应的流速分别为0 m/s、0.807 m/s、1.253 m/s，则可求得对应的α=0.5、β=1.62、γ=-0.03。

1 a内流速u下的疲劳损伤为

(10)

式中：N(ε)为材料在一定循环交变应变幅下对应的最大应变循环次数，具体取值可通过材料ε-N曲线获得，应变幅ε由式(6)计算得到。

根据Palmgreen-Miner线性损伤累积理论，海缆在1 a中的总疲劳累积损伤为

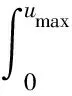
(11)

式中：umax为最大流速。

海缆的疲劳寿命为

(12)

3 海底电缆疲劳寿命仿真计算结果

使用数值模型计算时，原型海缆在空气中的振动阻尼比取0.05，将ε-N曲线进行分段拟合共8段。表1和表2为输入的模型参数。

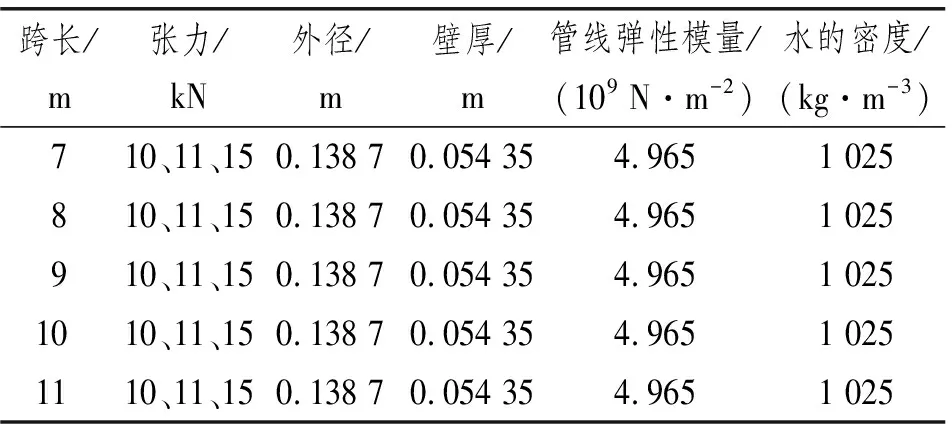
表1 输入模型参数

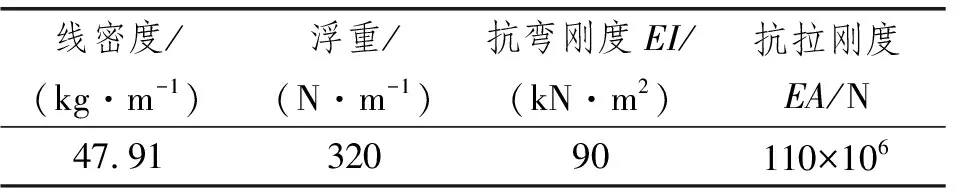
表2 其他输入模型参数

输入相关参数后，输出不同流速下振动响应频率、最大振幅比、跨中或1/4跨长处疲劳累积损伤及应力和应变幅。依据计算数据绘制累积损伤曲线和不同跨长下疲劳寿命曲线。

在进行疲劳分析时，将电缆结构简化为4层(见图2)，沿径向选取3个不同的位置作为计算参考点。其中：1号计算点位于铜导体层的最外侧(半径r=0.022 30 m)，采用铜ε-N曲线分析疲劳；2号计算点位于铠装层的最外侧(半径r=0.065 35 m)，采用铅合金ε-N曲线和铜ε-N曲线分析疲劳；3号计算点位于铅合金护套层的最外侧(半径r=0.056 65 m)，采用铅合金ε-N曲线分析疲劳。考虑到2号计算点采用铅合金ε-N曲线对疲劳寿命影响最大，为此主要对2号计算点(材料取铅合金)进行疲劳分析。

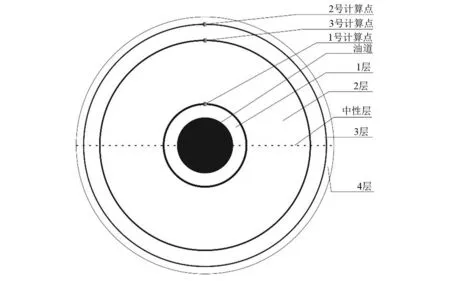
图2 电缆结构简化

3.1 张力T=10 kN时海底电缆累积损伤计算结果

对于张力T=10 kN工况，跨长L=8 m、11 m 海缆原型振幅比和累积损伤计算结果如表3和表4所示，计算中最大流速取umax=2.0 m/s，Smax为海缆单位截面受到的最大应力。

表3 海缆原型振幅比和2号计算点累积损伤计算结果(L=8 m、T=10 kN)

表4 海缆原型振幅比和2号计算点累积损伤计算结果(L=11 m、T=10 kN)

由表3和表4可知，跨长L=8 m、11 m的海缆振动主模态(主响应频率对应的振动模态)为一阶。海缆跨长8 m对应的一阶主模态起振流速为1.6 m/s，随着跨长增大，对应的一阶主模态起振流速减小。当跨长L=8 m、11 m的海缆对应的最大流速大于2.0 m/s时，疲劳寿命大于40 a(对应的累积损伤应小于0.025)。

3.2 张力T=11 kN时海底电缆累积损伤计算结果

对于张力T=11 kN工况，跨长L=8 m、11 m 海缆原型振幅比和累积损伤计算结果如表5和表6所示。最大流速取umax=2.0 m/s。

表5 海缆原型振幅比和2号计算点累积损伤计算结果(L=8 m、T=11 kN)

表6 海缆原型振幅比和2号计算点累积损伤计算结果(L=11 m、T=11 kN)

由表5和表6可知，跨长L≤11 m的海缆振动主模态(主响应频率对应的振动模态)为一阶。跨长8 m对应的一阶主模态起振流速为1.64 m/s，随着跨长增大，对应的一阶主模态起振流速减小。若疲劳寿命按大于40 a考虑(对应表5和表6中的累积损伤应小于0.025)，跨长8 m的海缆对应的最大流速为1.76 m/s、11 m的海缆对应的最大流速大于2.0 m/s。

3.3 张力T=15 kN时海底电缆累积损伤计算结果

对于张力T=15 kN工况，跨长L=8 m、11 m 海缆原型振幅比和累积损伤计算结果如表7和表8所示，最大流速取umax=2.0 m/s。

表7 海缆原型振幅比和2号计算点累积损伤计算结果(L=8 m、T=15 kN)

表8 海缆原型振幅比和2号计算点累积损伤计算结果(L=11 m、T=15 kN)

由表7和表8可知，跨长L≤10 m的海缆振动主模态(主响应频率对应的振动模态)为一阶。跨长8 m对应的一阶主模态起振流速为1.72 m/s，随着跨长增大，对应的一阶主模态起振流速减小。当最大流速为2.0 m/s时，跨长L≤10 m的海缆的疲劳寿命都大于40 a。由表8可知，跨长11 m的海缆在流速较大时的振动主模态为二阶，其最不利的累积损伤由1/4跨长处的应变控制，最大流速1.52 m/s 时疲劳寿命大于40 a。

3.4 不同弹性模量和阻尼比下海底电缆累积损伤计算结果

在第3.1节～第3.3节的疲劳寿命数值仿真计算中选取的原海缆动态抗弯刚度EI=90 kN·m2，弹性模量E0=4.965×109N/m2，阻尼比为0.05。为考察弹性模量对数值预报结果的影响，计算时分别取弹性模量为0.75E0、1.00E0、1.25E0。张力T=10 kN、跨长L=8 m的海缆原型振幅比和累积损伤计算结果(E=0.75E0)如表9所示，最大流速取umax=2.0 m/s。(节选列出部分数据。)

表9 海缆原型振幅比和2号计算点累积损伤计算结果(E=0.75E0)

弹性模量0.75E0对应的一阶主模态起振流速为1.48 m/s，随着弹性模量增大，对应的一阶主模态起振流速增加。若疲劳寿命按大于40 a考虑(对应累积损伤应小于0.025)，随着弹性模量的增加，疲劳寿命大于40 a所对应的最大流速增加。

在第3.1节～第3.3节的疲劳寿命数值仿真计算中选取的原海缆阻尼比为0.05。为考察阻尼比数值预报结果的影响，计算时分别取阻尼比为0.02、0.05、0.09。张力T=10 kN、跨长L=8 m的海缆原型振幅比和累积损伤计算结果(ξ=0.02)如表10所示，最大流速取umax=2.0 m/s。(节选列出部分数据。)

表10 海缆原型振幅比与2号点累积损伤计算结果(ξ=0.02)

阻尼比为0.02对应的一阶主模态起振流速为1.60 m/s，随着阻尼比增大，对应的一阶主模态起振流速增加。若疲劳寿命按大于40 a考虑(对应累积损伤应小于0.025)，随着阻尼比增大，疲劳寿命大于40 a所对应的最大流速增加。

4 海底电缆疲劳寿命影响因素分析

以2号计算点(材料取铅合金)为例，分析张力和跨长对海缆疲劳寿命的影响，数值仿真模型输入原型参数如表11所示。选取的弹性模量为E0=4.965×109N/m2，阻尼比为0.05。

表11 数值仿真模型输入原型参数

4.1 张力和跨长对海底电缆疲劳寿命的影响

通过分析可得，海缆跨长、张力变化引起起振流速及应变幅峰值对疲劳寿命有较大影响。表12为起振流速分布。

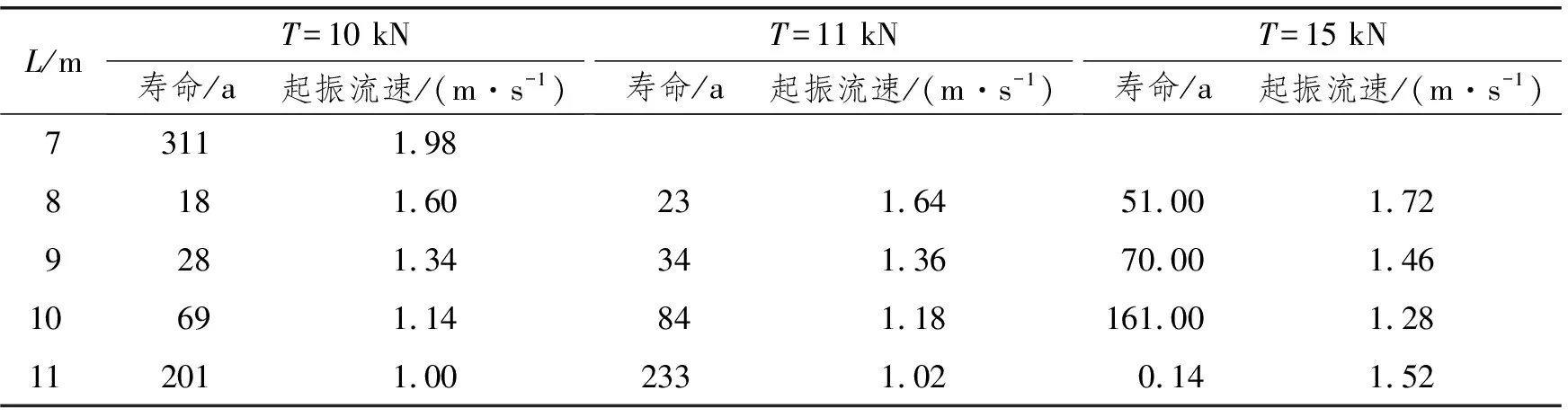
表12 海缆疲劳寿命分布(umax=2.0 m/s)

表13为最大流速umax=1.7 m/s情形，跨长L=7～11 m海缆原型对应不同张力的疲劳寿命分析结果。由表12与表13的数据对比可知，降低所采用的最大流速，可增加海缆的疲劳寿命。

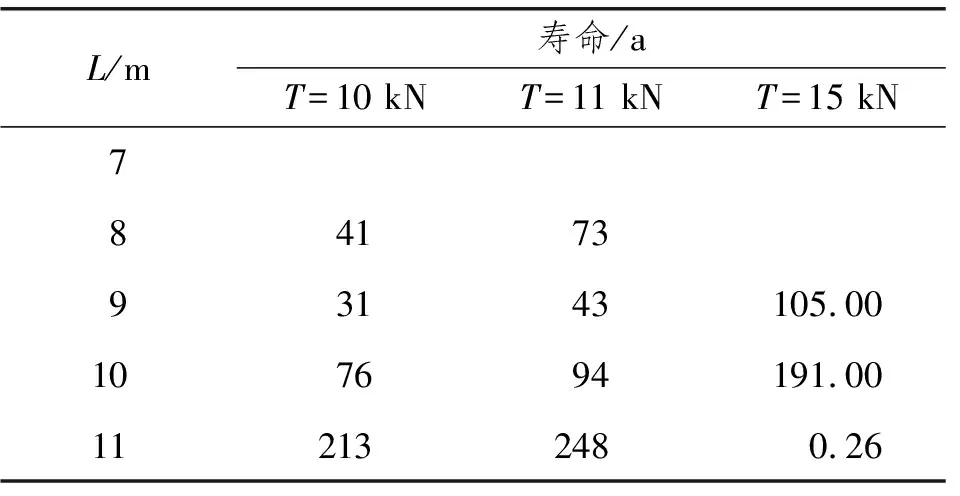
表13 海缆疲劳寿命分布(umax=1.7 m/s)

图3为最大流速为2.0 m/s和1.7 m/s情形下跨长7～11 m海缆原型对应11 kN张力的疲劳寿命沿轴向分布。图4为最大流速2.0 m/s和1.7 m/s下跨长7～11 m海缆原型对应15 kN张力的疲劳寿命沿轴向分布，图5为相应的疲劳损伤沿轴向分布。数值结果所表现的变化规律与挪威科技大学Carl M.Larsen团队在考虑流速概率分布时所得到的规律吻合。图3～图5中跨长比即计算点所在位置距海缆悬跨起点的长度与跨长L的比值。

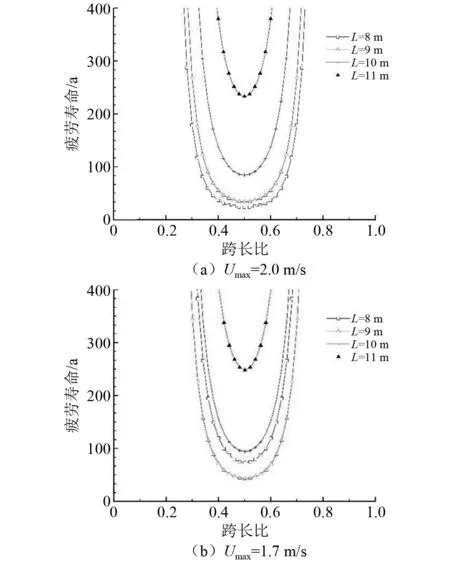
图3 疲劳寿命沿轴向分布(T=11 kN)

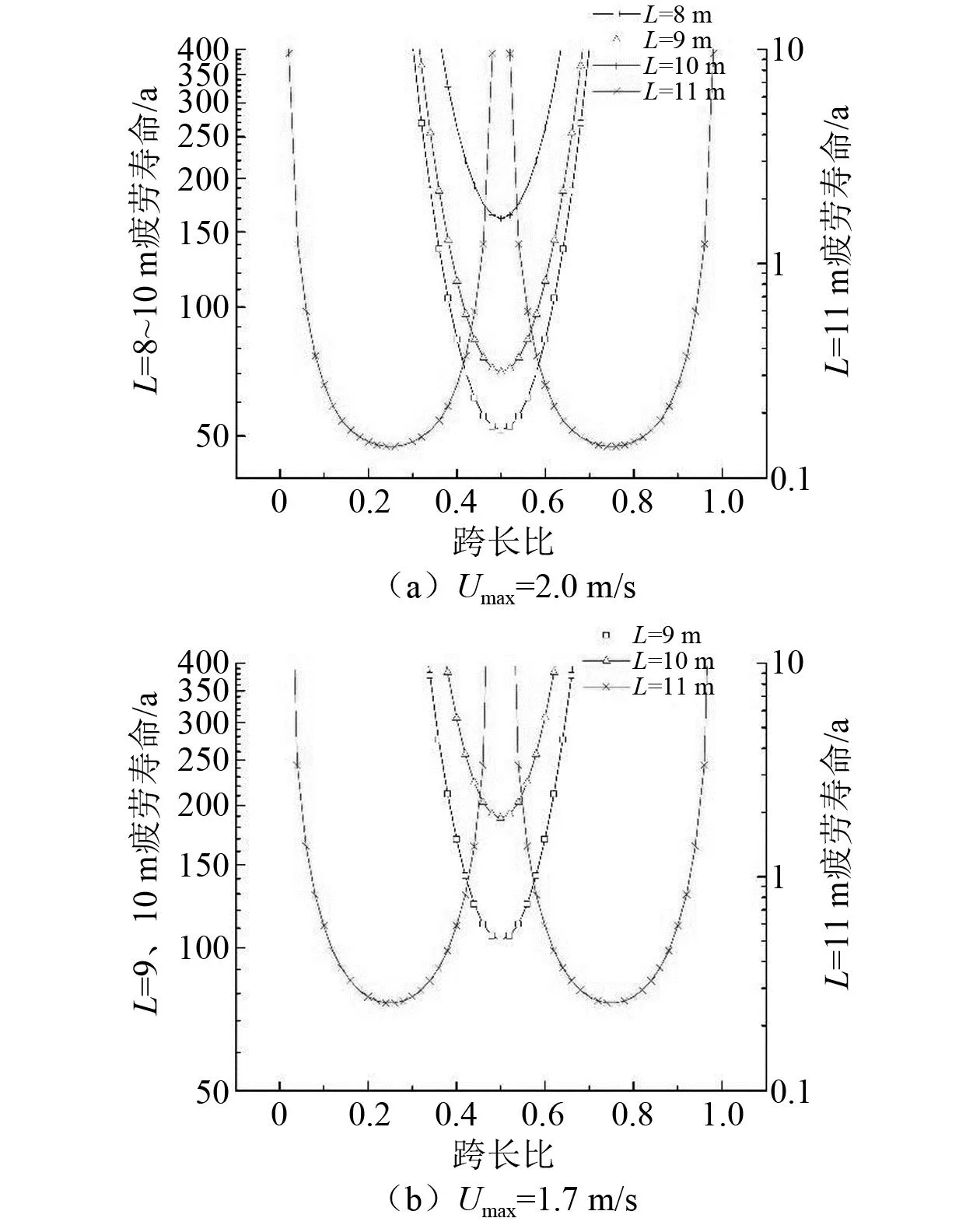
图4 疲劳寿命沿轴向分布(T=15 kN)

图5 累积损伤沿跨长分布(T=15 kN)

4.2 弹性模量、阻尼比对海底电缆疲劳寿命的影响

表14为跨长L=8 m、张力T=10 kN、阻尼比ξ=0.05条件下，当最大流速umax=2.0 m/s时，海缆原型对应不同刚度的疲劳寿命分析结果。

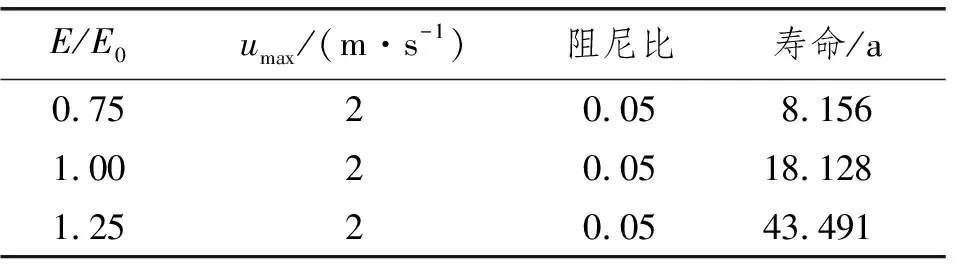
表14 海缆疲劳寿命分布(L=8 m、T=10 kN、ξ=0.05)

由表14可知，在此条件下，弹性模量E/E0=0.75、1.00、1.25所对应的海缆疲劳寿命分别为8 a、18 a和43 a，即当海缆刚度增大时，相同跨长的海缆疲劳寿命延长。

表15为跨长L=8 m、张力T=10 kN条件下，当最大流速umax=2.0 m/s时，海缆原型对应不同阻尼比的疲劳寿命分析结果。

表15 海缆疲劳寿命分布(L=8 m、T=10 kN、E/E0=1)

由表15可知，在此条件下，当海缆刚度相同(E/E0=1.0)时，阻尼比ξ=0.02、0.05和0.09所对应的海缆疲劳寿命分别为7 a、18 a和409 a，即当阻尼比增大时，相同跨长海缆的疲劳寿命延长。这是因为当阻尼比增大时，相同跨长海缆跨中位置的应变水平有所减小，其疲劳寿命有所延长。对于大阻尼情形，同一跨长海缆原型的疲劳寿命有显著延长。

4.3 材料和位置对海底电缆疲劳寿命的影响

随着海缆的内力随时间变化，其内部各层的应力(除中性层外)也随时间做周期性的变化，但由于铜、铅合金等易疲劳金属材料分布在距离中性层不同的位置上，因此各层的疲劳寿命也不同。分别对铜和铅合金及不同计算点下铅合金的疲劳特性进行分析。

图6为跨长L=8 m，最大流速umax=2 m/s，张力T=10 kN、11 kN、15 kN条件下，2号计算点处海缆疲劳寿命沿电缆轴向的分布。

图6 铠装铜线和铅合金疲劳寿命沿轴向分布

由图6可知，在不同张力条件下电缆轴向各点处，铜线的疲劳寿命大于铅合金，铜线和铅合金的疲劳寿命控制点均为跨中，且疲劳寿命从跨中到两端逐渐增大。

表16为不同张力条件下铜线和铅合金控制点处疲劳寿命分布。在相同工况下，控制点处铠装铜线的疲劳寿命远大于铅合金，约为铅合金的80倍。这是由于铜和铅合金材料的疲劳特性曲线不同，在相同应变下发生疲劳破坏时，铜能承受更大次数的循环应变。

表16 铠装铜线和铅合金控制点处疲劳寿命分布

图7为铅合金分别在跨长L=8 m，最大流速umax=2.0 m/s，张力T=10 kN、11 kN、15 kN条件下，2号、3号计算点处的疲劳寿命沿轴向分布。由图7可知，在不同张力条件下电缆轴向各点处，3号计算点的铅合金疲劳寿命均大于2号计算点，跨中位置为铅合金疲劳寿命控制点，且疲劳寿命从跨中到两端逐渐延长。

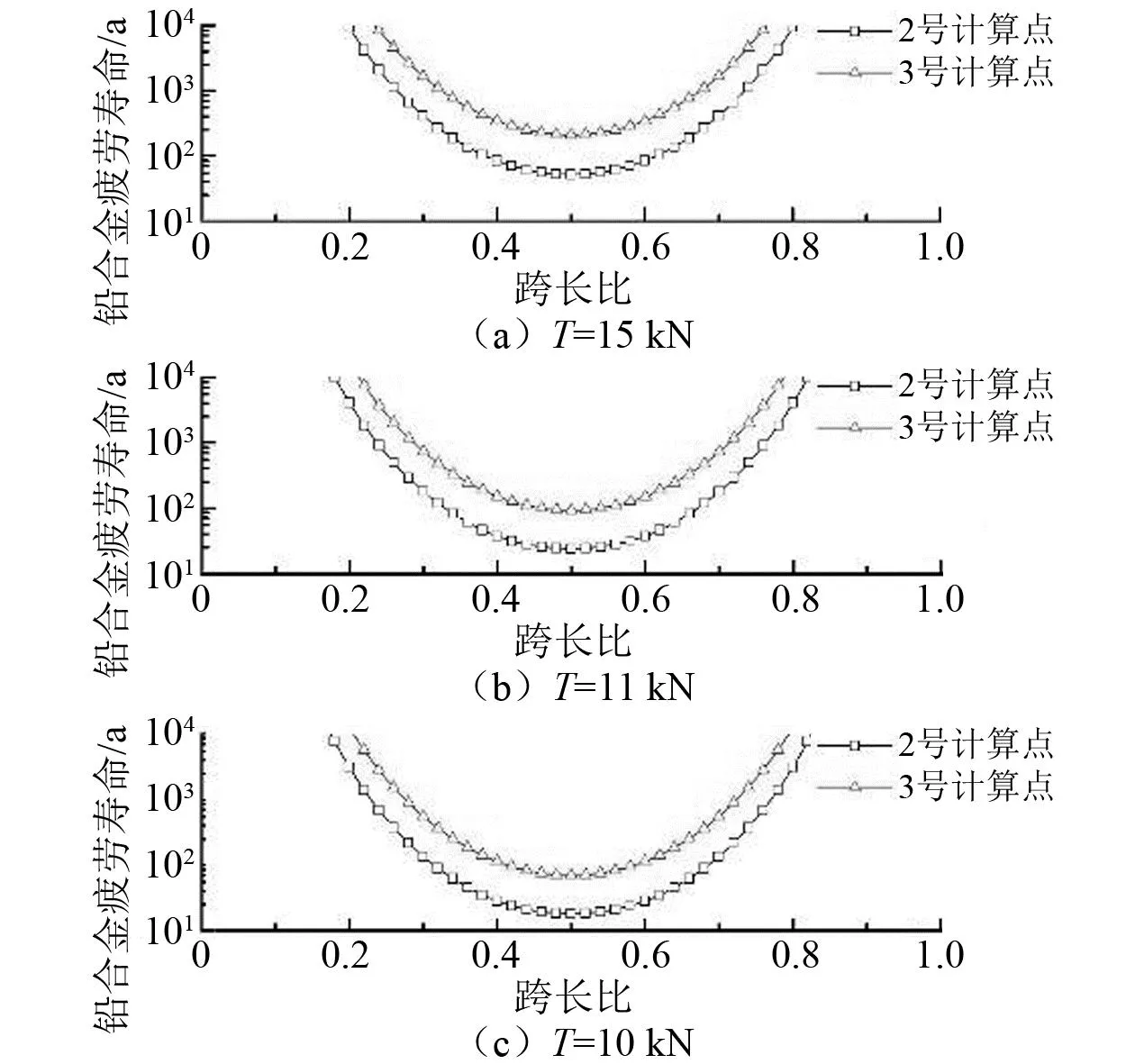
图7 2号和3号计算点处铅合金疲劳寿命沿轴向分布

表17为不同张力条件下2号和3号位置铅合金的控制点处疲劳寿命分布。

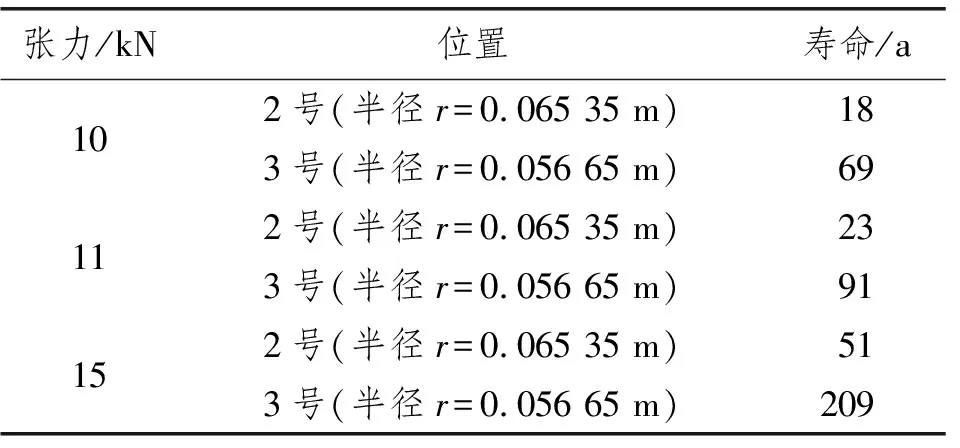
表17 2号和3号计算点铅合金控制点处疲劳寿命分布

在理论上应对铜导体、铅合金护套和铠装铜线分别进行疲劳损伤计算分析，由于模型中假定海缆为均质圆柱体，振动过程中所产生应变沿中性层至外侧(垂直于中性层方向)线性分布，中性层处应变幅为零，铠装铜线处应变幅最大，但在实际计算中，由于2种材料疲劳特性不同，在各工况下铠装铜线的疲劳寿命至少为铅合金护套的10～102倍，因此，海缆的疲劳寿命由铅护套控制。

4.4 外径和重量对海底电缆疲劳寿命的影响

为研究外径和单重对海缆疲劳寿命的影响，对外径和单重变化时500 kV海底电缆的疲劳寿命进行计算，边界条件取跨长L=8 m、流速u=2 m/s、张力T=10 kN、阻尼比ξ=0.05。计算结果如表18和表19所示。

表18 外径变化对海缆疲劳寿命的影响

随外径增大，海缆起振流速显著增加，发生涡激振动的流速区间减小，响应振幅比无显著变化，由于响应频率下降，一个时间序列内的振动次数减少，因此海缆疲劳寿命随外径增加而延长。

随海缆单位长度质量增加，海缆自振频率下降，通过分析其无量纲频率可知，起振流速降低，发生涡激振动的流速区间增大，因此海缆疲劳寿命随海缆单位长度质量增加而缩短。

为研究外径和单重对海缆疲劳寿命的影响，对110 kV和220 kV海底电缆疲劳寿命进行计算，计算参数如表20所示，并与500 kV海底电缆进行对比。

表20 计算参数

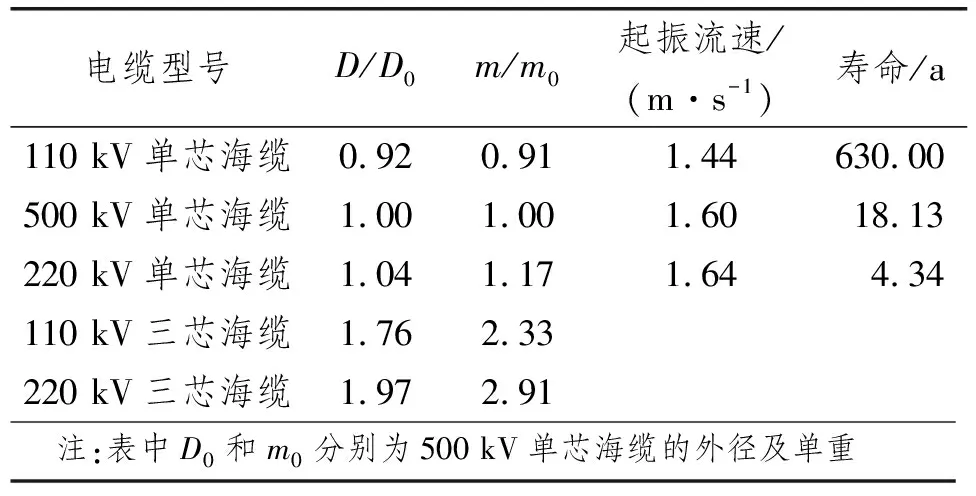
表21 外径、单重对疲劳寿命的影响

为研究外径和单重变化时海底电缆疲劳寿命的变化规律，在跨长L=8 m、流速u=2 m/s、张力T=10 kN、阻尼比ξ=0.05条件下，分别计算110 kV单芯海缆、110 kV三芯海缆、220 kV单芯海缆、220 kV三芯海缆和500 kV单芯海缆的疲劳寿命。计算结果如21表所示。

由计算结果可知：与500 kV单芯海缆相比，当其他条件不变时，110 kV和220 kV三芯海缆在流速2 m/s以内未发生振动响应；当振动发生时，对于110 kV、220 kV和500 kV单芯海底电缆，随外径、单重的增加，起振流速增加，疲劳寿命不断缩短。

5 结 论

(1)跨长增加对控制疲劳损伤的不同参数的影响表现为不同的规律，从而导致累积疲劳损伤和疲劳寿命随跨长变化表现为非单调的变化规律。

(2)当海缆刚度增大时，相同跨长的海缆疲劳寿命延长；当阻尼比增大时，相同跨长的海缆疲劳寿命延长。

(3)在不同张力条件下电缆轴向各点处，铜线的疲劳寿命大于铅合金，铜线和铅合金的疲劳寿命控制点均为跨中，且疲劳寿命从跨中到两端逐渐延长。在相同工况下，控制点处铠装铜线的疲劳寿命远大于铅合金。

(4) 当振动发生时，随海缆外径、单重的增加，起振流速增加，疲劳寿命缩短。

根据海底电缆振动及疲劳寿命的分析结论，为降低涡激振动对海底电缆疲劳寿命的影响，建议采取以下措施：在电缆结构参数方面，结合海缆的材料和制造工艺，适当增加海缆的弹性模量和阻尼比。