构型对正多边形蜂窝异面缓冲性能的影响

关天进，孙玉瑾，孙德强，杜强强，骆泽龙，李金塘

构型对正多边形蜂窝异面缓冲性能的影响

关天进1，孙玉瑾2，孙德强2*，杜强强2，骆泽龙2，李金塘2

（1.深圳龙腾印刷技术服务有限公司，广东 深圳 518000；2.陕西科技大学 a.轻工科学与工程学院 b. 轻化工程国家级实验教学示范中心 c. 3S包装新科技研究所，西安 710021）

利用有限元法研究应变率不敏感的双线性各向同性应变硬化正多边形（等边三角形、正方形、正六边形和正八边形）蜂窝的异面缓冲性能。建立基于正多边形蜂窝特征单元的异面冲击分析有限元模型，提出最佳应变这一缓冲性能评价新指标，基于此重新定义各能量吸收评价指标，形成新缓冲性能评价方法。以此获取不同相对密度的各正多边形蜂窝在不同冲击速度下的变形模式和应力-应变曲线，以及平均平台应力、比能量吸收和冲击力效率等评价指标值，并进行了分析。给定相对密度下，正八边形蜂窝具有最大的异面平均平台应力；正多边形蜂窝的比能量吸收与冲击速度成二次关系；定密度的正六和八边形蜂窝的冲击力效率优于等边三角形和正方形蜂窝。

正多边形蜂窝；最佳应变；变形模式；平均平台应力；最佳比能量吸收；冲击力效率

蜂窝材料因轻质、性优，用作夹芯材料，在航空、包装、交通运输等领域被广泛应用[1]。蜂窝优异的能量吸收特性，能够大大降低因冲击、跌落、碰撞等因素引起的物体损坏。蜂窝缓冲性能主要表现在共异面方向、异面方向具有更高的平台应力和更强的能量吸收。常见蜂窝构型有三角形、四边形、六边形、圆形、八边形等，宫晓博等[2]分析了3种蜂窝的共面动态力学性能；张豪等[3]对比分析了圆形、六边形等蜂窝的异面压缩性能和爆炸载荷作用下的变形过程；白临启等[4]研究了冲击载荷下箭头型负泊松比蜂窝的动态吸能性能。有限元法相比于试验法有更多优点，广泛应用于蜂窝力学分析，研究表明构型和冲击速度是影响蜂窝力学性能的重要因素[5-11]。缓冲应用中缓冲常承受高速载荷作用，例如包装件跌落冲击速度可达10 m/s以上，高速汽车撞击防护栏会达到50～60 m/s，宇宙飞船星球着陆和高速列车行驶时的速度会达100 m/s以上。本文选取等边三角形、正方形、正六边形和正八边形蜂窝为研究对象，利用有限元软件ANSYS/ LS-DYNA进行仿真计算，对比分析它们在3～250 m/s的速度范围内的异面缓冲性能。

1 异面缓冲分析有限元法

1.1 正多边形蜂窝构型和相对密度

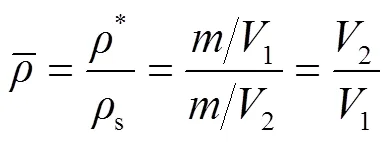
式中：1为蜂窝结构总体积；2为蜂窝基材净体积；为蜂窝质量。

图1的各构型蜂窝中，虚线框围住的部分为其特征单元。基于这些特征单元，根据式（1）可得：

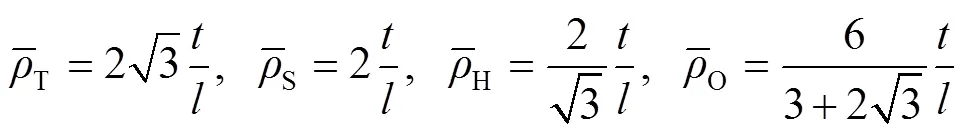
1.2 异面缓冲性能分析有限元模型

参照已有的二维多孔材料冲击分析的有限元建模方法[5-11]，建立各正多边形蜂窝异面冲击分析的有限元模型，在此使用了相类似的模型。以正六边形蜂窝为例，其异面冲击分析的有限元模型如图2所示，样品被放置在2个刚性压板P1和P2之间，上压板P1以恒定的速度沿3负方向移动，直到样品被完全压溃，下压板P2固定不动（图2a）。4种正边形蜂窝的样品，是基于图1中各蜂窝的特征单元而建立的。为了以此模拟大尺寸蜂窝的受力状态，要对样品施加周期性边界条件，对各多边形蜂窝样品来说施加方式基本类似。就拿正六边形蜂窝样品来说，其异面俯视图如图2b所示，以样品几何模型的3条外边线为'3轴建立局部坐标系，其余2个局部坐标轴为'1和'2，其中'1轴垂直于相应外边线且位于该边线所在的壁面内，'2轴垂直于相应外边线所在的壁面，3个坐标轴的位置关系符合右手法则。对3条边线上的节点来说，周期性边界条件均为沿'1方向的位移自由度为0，绕'2和'3方向无转动自由度。整个模型采用5个积分点的Belytschko-Tsay Shell163壳单元进行网格划分。样品被设置成单面自动接触（ASSC），静动摩擦因数分别为0.15和0.1；样品与压板P1和P2之间设置成面面接触（ASTS），静动摩擦因数分别为0.2和0.15。蜂窝结构基材采用应变率不敏感的理想弹塑性双线性各向同性应变硬化材料模型，典型代表是具有以下力学性能的某铝合金：弹性模量为68.97 GPa、屈服应力为292 MPa、正切模量为689.7 MPa、泊松比为0.35、密度s为2 700 kg/m3。纸张也可以近似为双线性应变硬化材料模型，例如典型纸材料参数：弹性模量为842 MPa，屈服应力为7.67 MPa，正切模量为150 MPa。无论选择纸张还是该铝合金材料参数，本研究所得最终结论都是一致的，故所有模型均选用该铝合金作为基材。所有模拟中，样品单元边长均满足=3 mm。

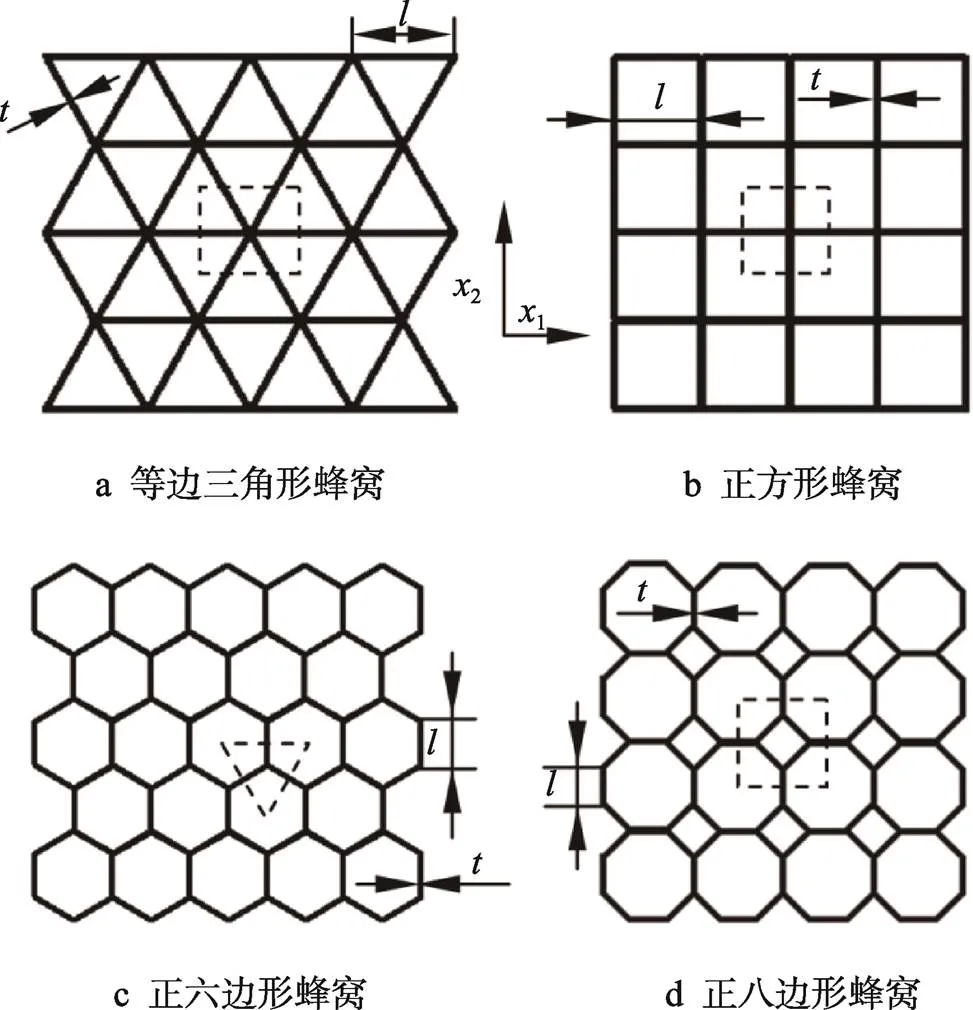
图1 正多边形蜂窝及其构型

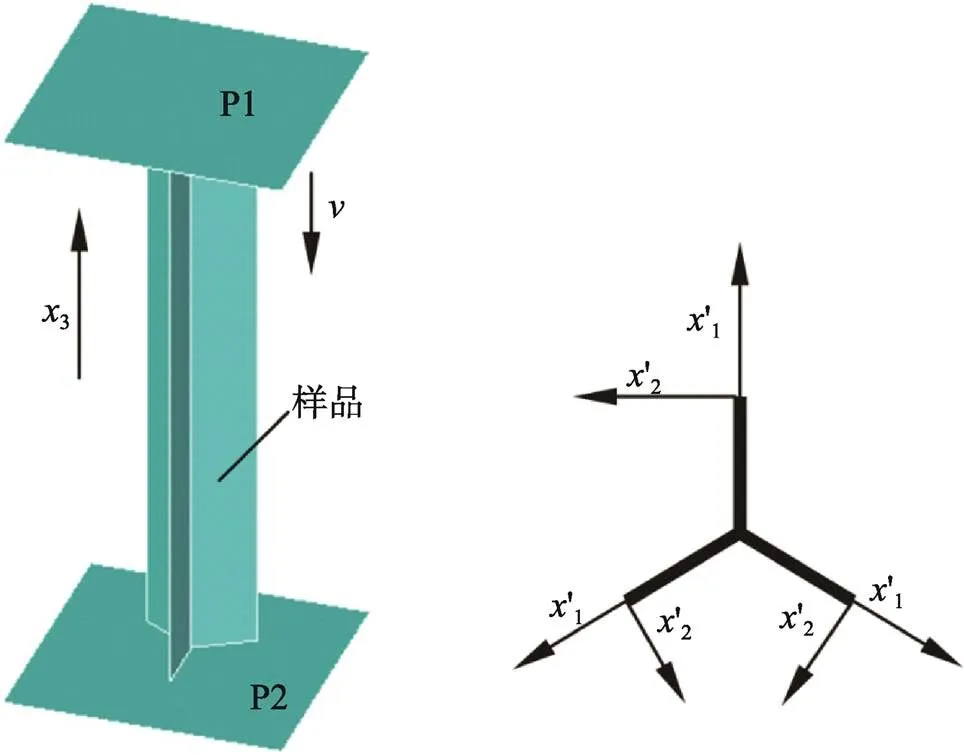
图2 正六边形蜂窝异面冲击分析有限元模型

为了消除样品的尺寸效应，尝试性模拟计算结果表明，当>8 mm时各缓冲性能指标受的影响可忽略，取=15 mm；当模型网格单元边长小于0.2 mm时，各缓冲性能指标趋于稳定，网格单元边长取0.08 mm。

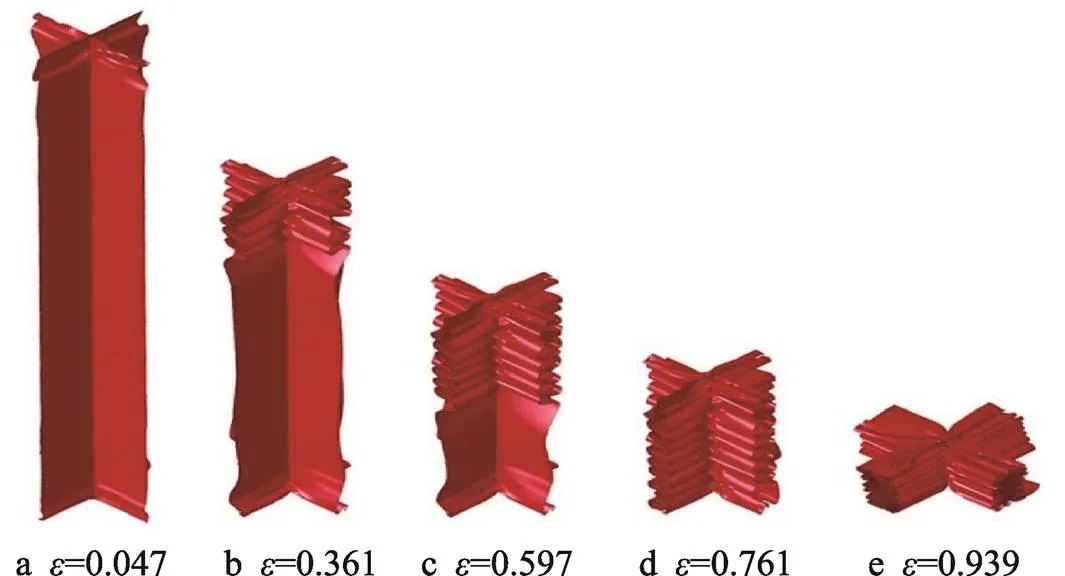
图3 正方形蜂窝的变形过程 (t=0.03 mm和v=50 m/s)

1.3 有限元模型的可靠性

为了验证有限元模型的可靠性，以正方形蜂窝为例，其典型的异面冲击变形过程如图3所示。样品顶部和底部同时发生折曲变形，冲击波传输的滞后性导致顶部折曲带衍生速度远大于底部的；上下折曲带按照一定折曲波长和衍生速度向中间发展，顶部折曲带不断向下推进；最后上下折曲带衔接在一起，将样品压实。此变形过程与Xue等[12]得到的变形模式相一致。在=0.03、0.05 和0.07 mm的情况下，4种构型蜂窝的类静态（=3 m/s）异面平均平台应力的有限元计算结果如图4所示。图4还同时绘出了Zhang等[13]理论公式的相应计算结果，理论与有限元计算结果相比误差小于5%，证明了有限元模型的可靠性。

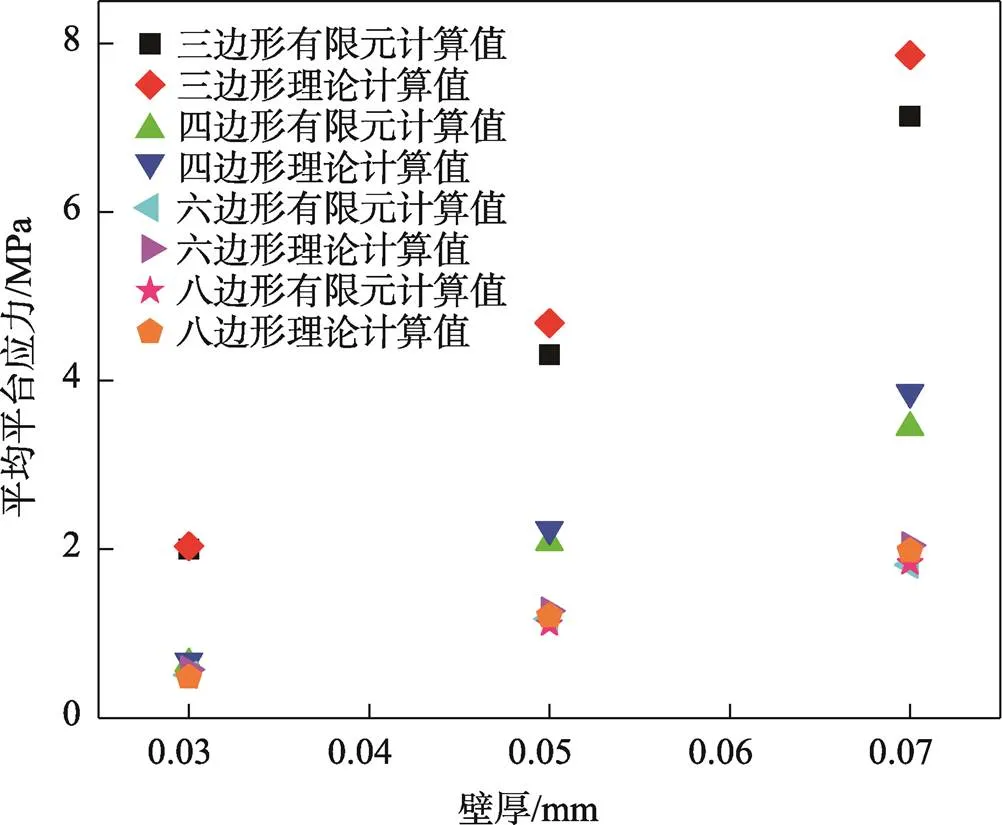
图4 正多边形蜂窝异面类静态平均平台应力理论和有限元值

2 基于最佳应变的缓冲性能评价方法

通过软件LS-PrePost得到样品所有冲击响应曲线。假如为P1与样品间的接触力，为P1的位移，0为样品异面等效横截面积，0为样品异面初始长度，则应力和应变计算见式（3）。[10]

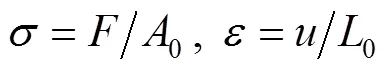
在任一应变a下，样品的单位体积能量吸收为[10]：

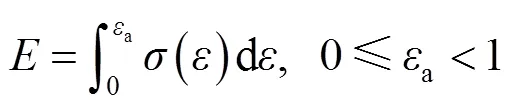
假设与a对应的应力为a，则对应的能量吸收效率e可以定义为[11]：

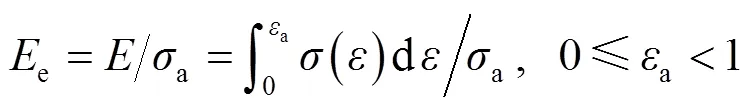
e在物理上反映了样品在一定应力水平下的能量吸收效果。

比能量吸收e指单位质量的能量吸收，任一应变a对应的e表示为[11]：

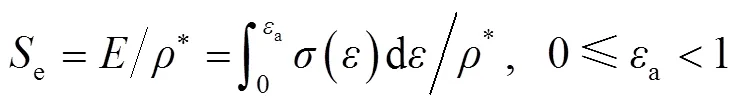
2.1 最佳应变

蜂窝异面冲击-曲线包括4个典型的阶段：线弹性阶段、屈服阶段、平台应力阶段和密实化阶段。平台应力阶段向密实化阶段转变时的应变称为密实化应变，常采用各种理论方法来确定它。理论方法确定的密实化应变，总是小于实际的密实化应变。实际缓冲应用中，如果材料变形越过理论密实化应变，至实际密实化应变后其应力就会达到一个很大的值，已无法起到最佳缓冲防护作用。在实际与理论密实化应变之间存在一个最合适的应变，定义为最佳应变M[14]。

M是由-曲线得到的，以等边三角形蜂窝为例，典型中低速冲击的-曲线（=0.03 mm和=50 m/s）如图5所示。图5a中线弹性阶段变形很小至初始峰应力0（相应0）之后应力急剧下降至一个低水平，接着是长的平台区阶段，在密实化阶段应力急剧上升，很快超过0。密实化阶段应力0所对应的应变即为M。相应地，图5b中的-曲线，M对应该曲线拐点后的点，此时最大应力max=0。

高速异面冲击时，-曲线平台应力阶段的应力随增加波动越剧烈。图6c为等边三角形蜂窝典型高速冲击异面-曲线，在密实化之前弹性阶段过后的屈服阶段出现一个局部最大值点，此时应力为max。同样，该最大应力在密实化阶段对应点，该点所对应的应变为M，如图5所示。

2.2 冲击力效率

-曲线上，M之前所有应力的平均值称为平均平台应力m，定义为[10,14]：

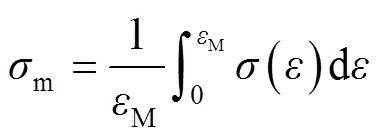
冲击力效率e，为平均平台应力m与最佳应变前的max的比值，即[10]：

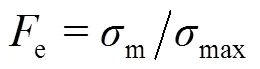
它用来评价蜂窝在冲击过程中应力的均匀性。e值越接近1，应力就越均匀。

2.3 最佳比能量吸收

M对应的比能量吸收，称之为最佳比能量吸收eO。根据式（1）、（4）、（6）和（7）可得eO为：

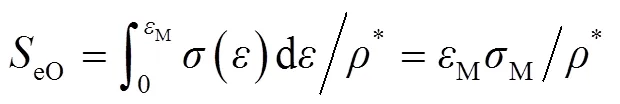
由此可见，评价正多边形蜂窝缓冲性能的上述指标均与eM相关，eM是表征其缓冲性能的重要指标。

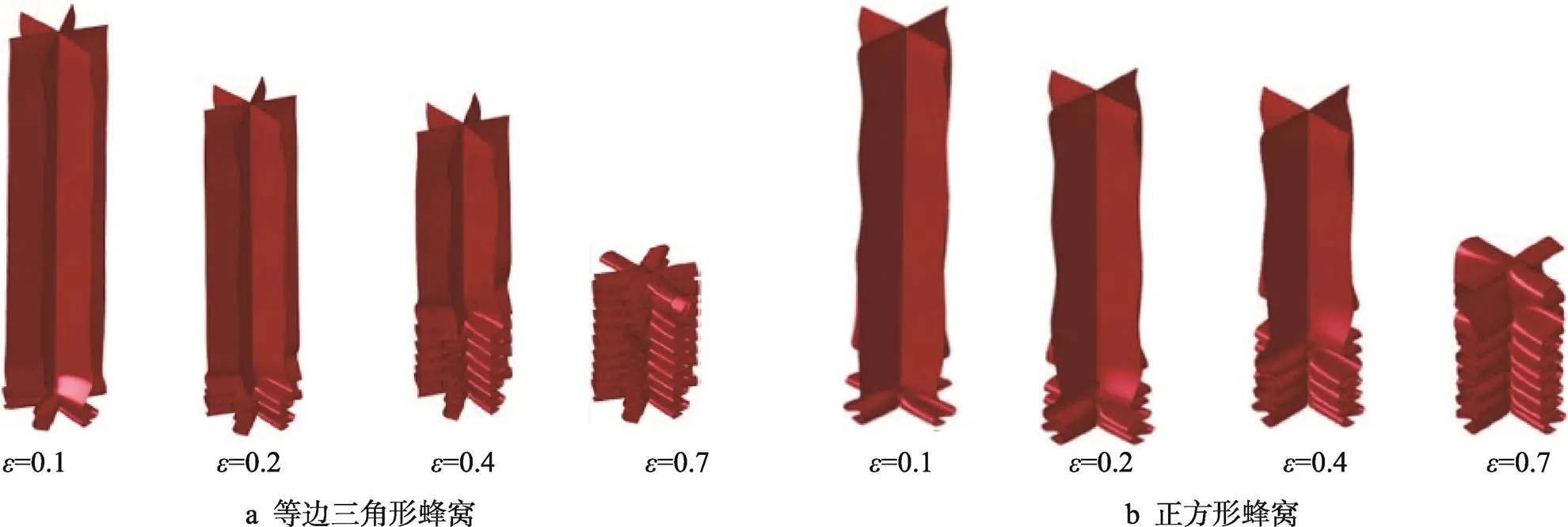
图6 定密度蜂窝异面低速冲击变形模式(=0.04和v=3 m/s)

3 变形模式

3.1 速度的影响

当=3 m/s的低速冲击时，正多边形蜂窝的变形模式如图6所示，相应的等效应力云图如图7所示。除正八边形外，其余3种构型蜂窝的变形都是从底部开始，并从下往上依次发生折曲变形，称之为准静态变形模式。正八边形之所以从顶部开始变形，是因为其构型所致，其特征单元中还有一个边长与八边形边长相同的正方形，其他构型蜂窝的特征单元中不含类似结构。正六边形和正八边形蜂窝在变形过程中应力分布情况也不同，当=0.005时，变形处于线弹性阶段末尾，应力大，样品应力主要集中在顶部和底部；当=0.02时，变形处于平台区阶段，蜂窝所受应力较线弹性阶段大幅下降，正六边形蜂窝的应力和变形集中在样品底部，并已从底部发生变形，而正八边形蜂窝的最大应力在顶部；随着应变进一步加大，样品应力集中在折曲带位置，这刚好对应了-曲线平台区应力的波动。

当=50 m/s的中速冲击时，图8所示的蜂窝变形模式不同于低速冲击时的变形模式，相应等效应力云图如图9所示。蜂窝均由上而下发生定波长折曲，称为过渡态变形模式。正方形和正八边形蜂窝样品的中间区域发生了明显折曲，使得变形与其他2种蜂窝的变形明显不同。从图9来看，当=0.005时，变形处于线弹性阶段，最大应力位于样品顶部；当=0.02时，等边三角形蜂窝已发生变形，顶部开始折曲，产生最大应力，从而进入平台区阶段，而此时正八边形蜂窝还处于线弹性阶段，还没有产生明显变形，但应力已扩散至底部。随着应变的增大，应力在样品底部逐步增大，但折曲变形还是集中在顶部，并且等边三角形蜂窝的折曲数目较其他构型的要多，这与相同密度下等边三角形蜂窝壁厚较小有关，小壁厚导致小的折曲波长。

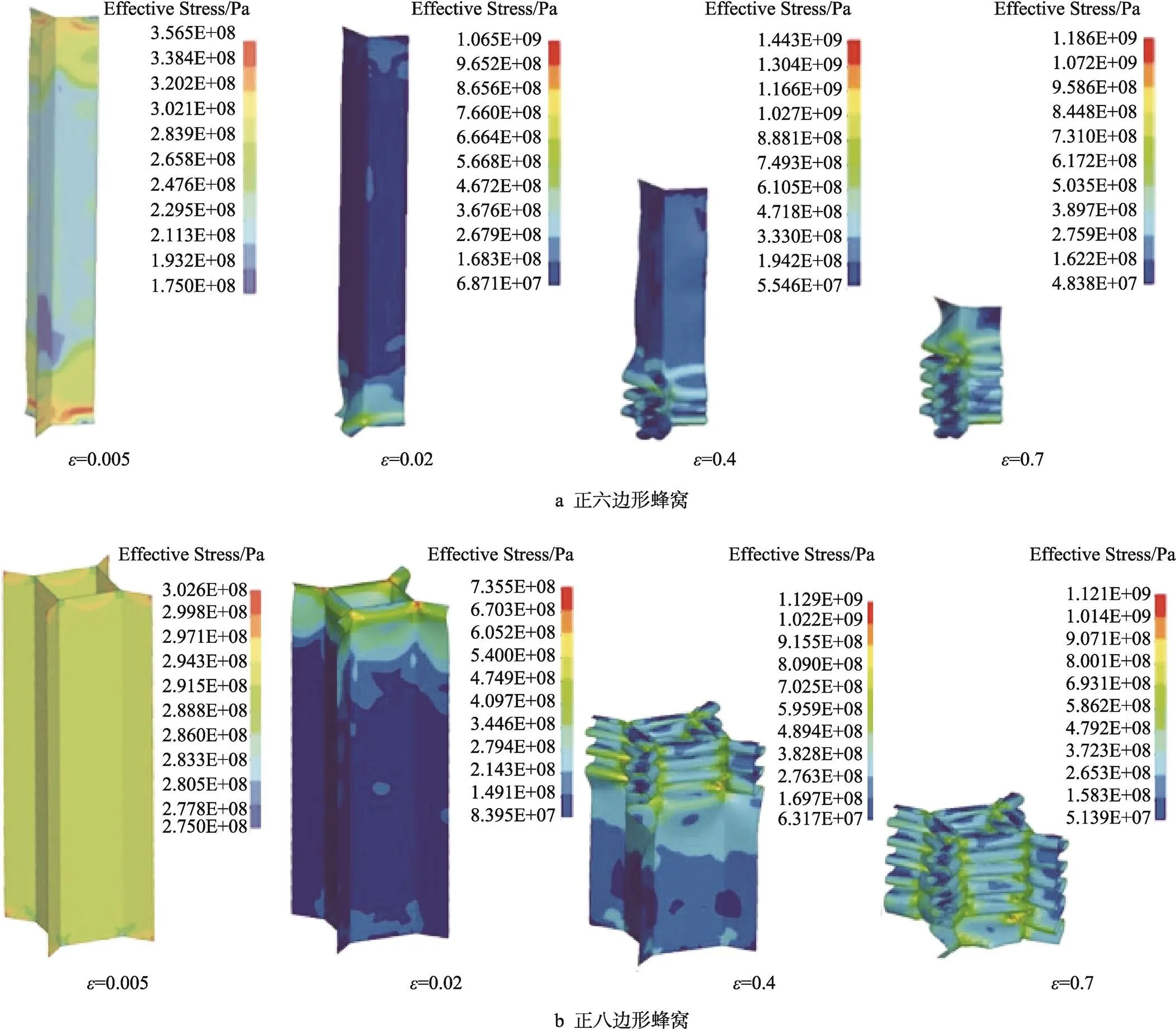
图7 定密度蜂窝异面低速冲击应力云图(=0.04和v=3 m/s)

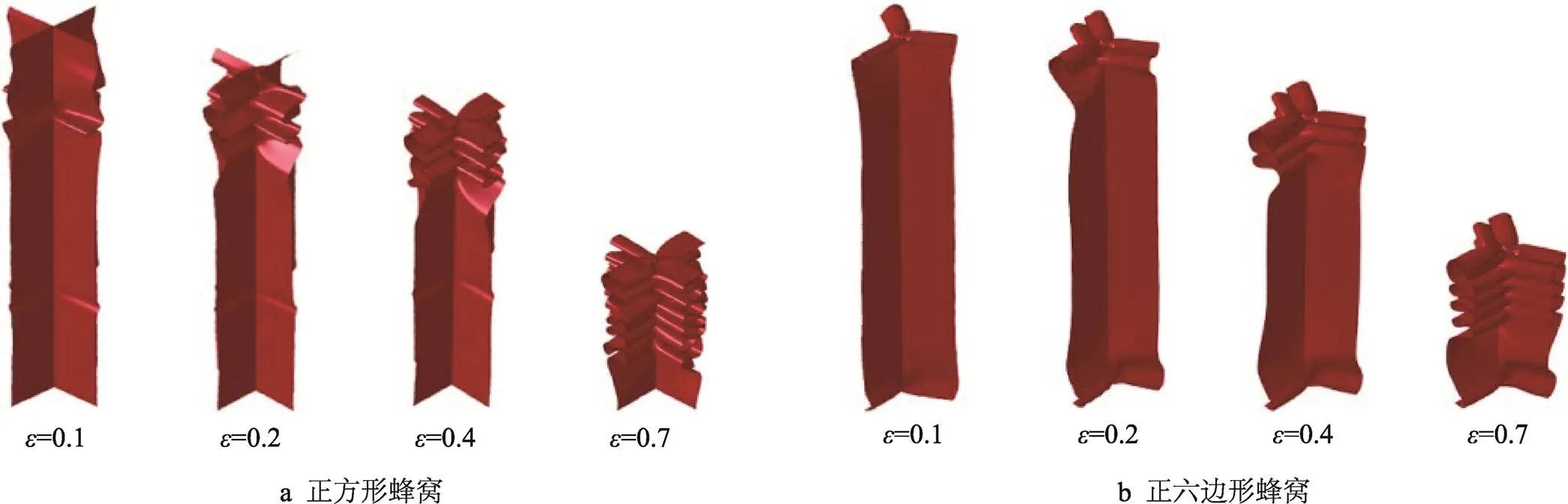
图8 定密度蜂窝异面中速冲击变形模式(=0.04和v=50 m/s)

图9 定密度蜂窝异面中速冲击应力云图(=0.04和v=50 m/s)

当=100 m/s的高速冲击时，各蜂窝的变形模式差别较大，如图10所示。此时的变形模式称为动态变形模式，变形除了从上至下发生渐近折曲外，底部也缓慢产生变形；正方形蜂窝样品中部也后于其顶部发生折曲变形，并且中部折曲带持续往下推进直至样品底部，而后顶部折曲带往下不断折曲，直至发生密实。正八边形蜂窝的变形自开始的很长时间里集中于底部，当变形到很大程度后其顶部变形才表现明显。

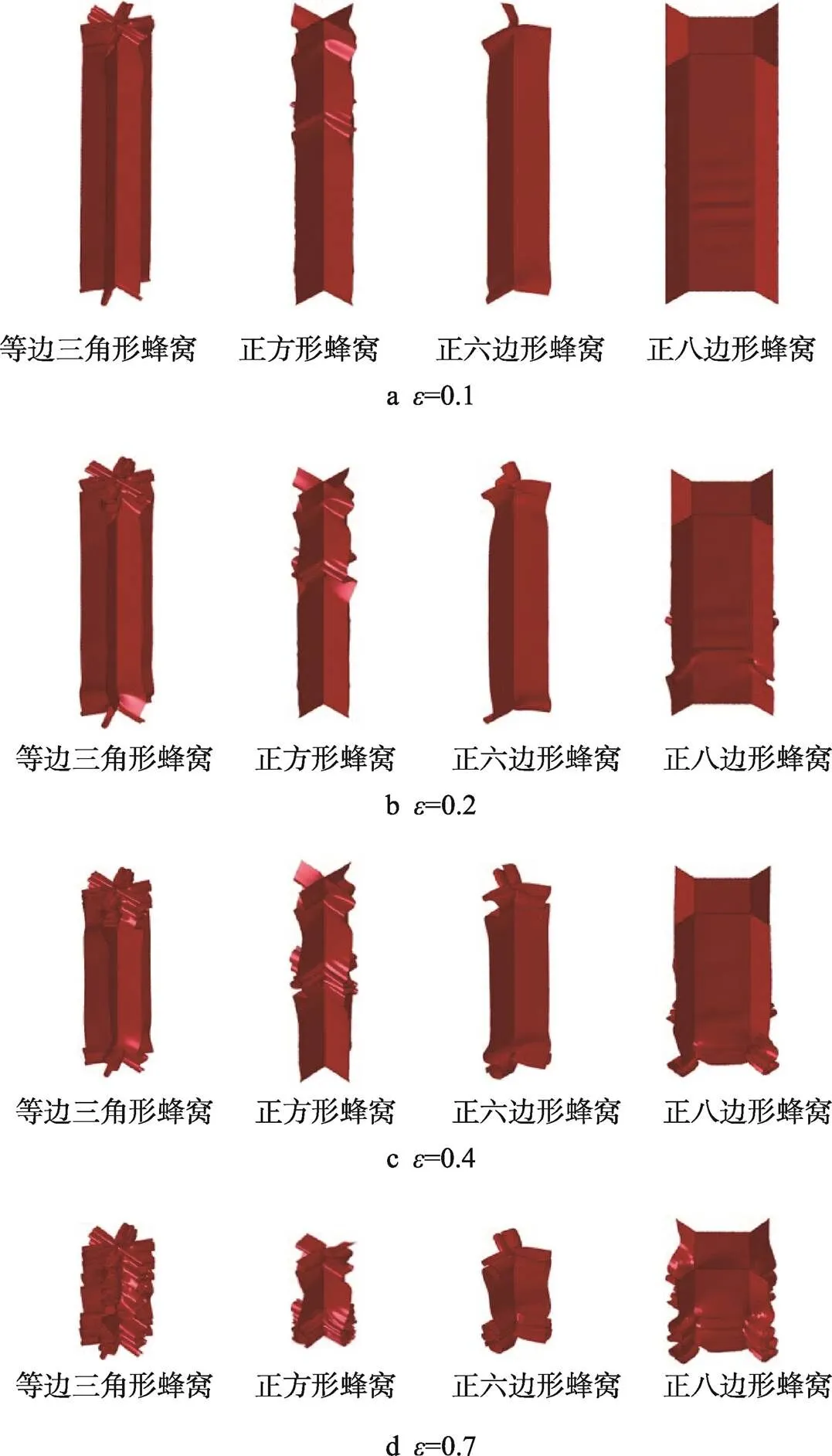
图10 定密度(=0.04)蜂窝高速异面变形模式(v=100 m/s）

3.2 壁厚的影响

选取4种壁厚的样品进行模拟计算，正六边形蜂窝的典型变形模式（=50 m/s下）如图11所示。同一速度下，壁厚的改变对变形模式几乎没有影响；但壁厚增大会使折曲波长变大，总折曲数目减少。4种壁厚正六边形蜂窝样品在=50 m/s的异面冲击下，均表现出自上往下过渡态变形模式。

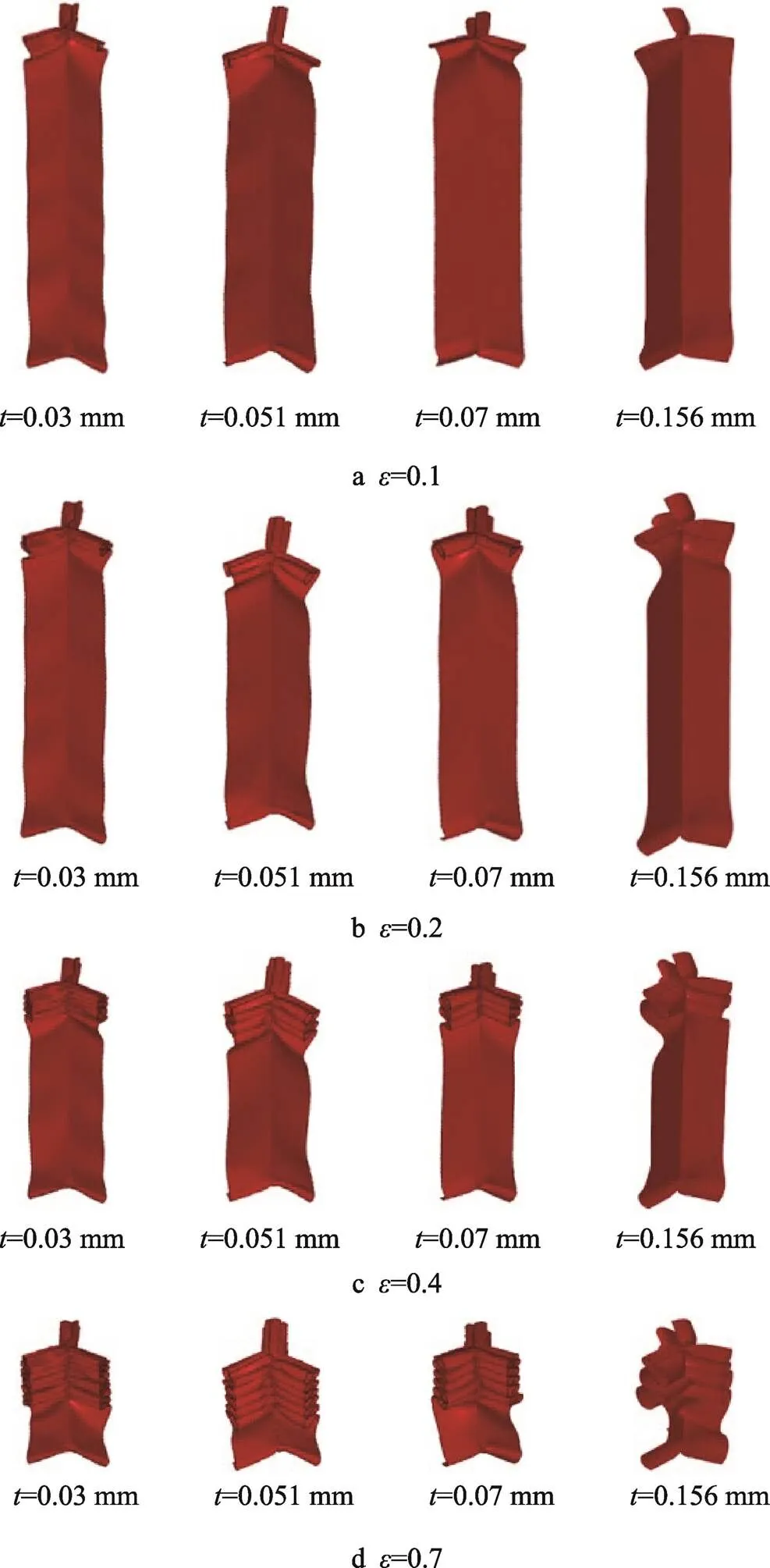
图11 不同壁厚正六边形蜂窝异面变形模式(v=50 m/s)

4 缓冲性能

4.1 s-e曲线

冲击速度影响变形模式，进而影响-曲线。图12a～c的-曲线对应图6、8和10低中高3种速度下的变形模式。在低速（=3 m/s）冲击条件下，等边三角形蜂窝初始峰应力值最小，平台区曲线最为平稳；正六边形和正八边形蜂窝的平台区较高，但波动较大（图12a）。在中速（=50 m/s）冲击条件下，4种构型蜂窝的初始峰应力值均有所增大，平台区曲线波动变大（图12b）。在高速（=100 m/s）冲击条件下，曲线的波动更加明显，正方形蜂窝的平台区相对平稳（图12c）。

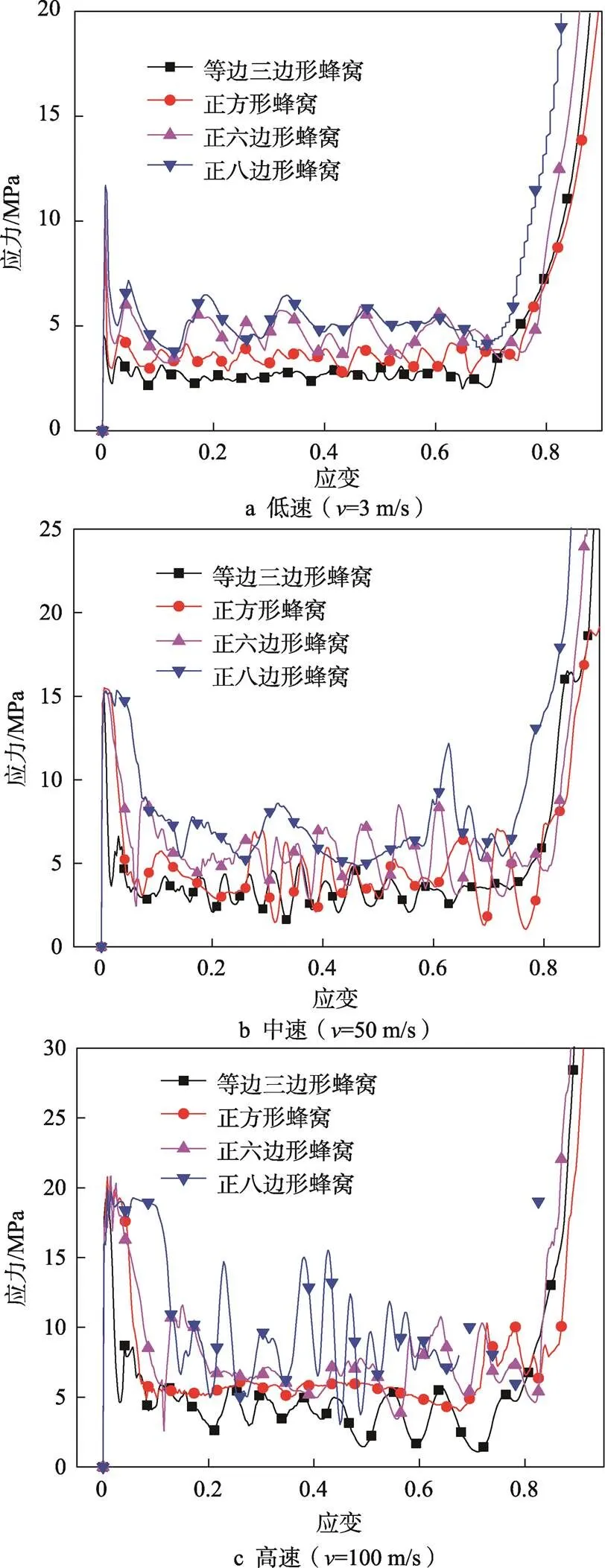
图12 定密度（=0.04）各正多边形蜂窝异面冲击的s-e曲线

4.2 平均平台应力

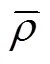
4种构型蜂窝的平均平台应力均随着冲击速度的增大而增大，同时/（相对密度）的增大使得平均平台应力也随之增加。在同一速度和相对密度下，正八边形蜂窝的平均平台应力高于其他构型蜂窝的，而等边三角形蜂窝的平均平台应力最低，平均平台应力值随蜂窝构型边数的增加而增大。

4.3 最佳比能量吸收

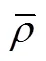
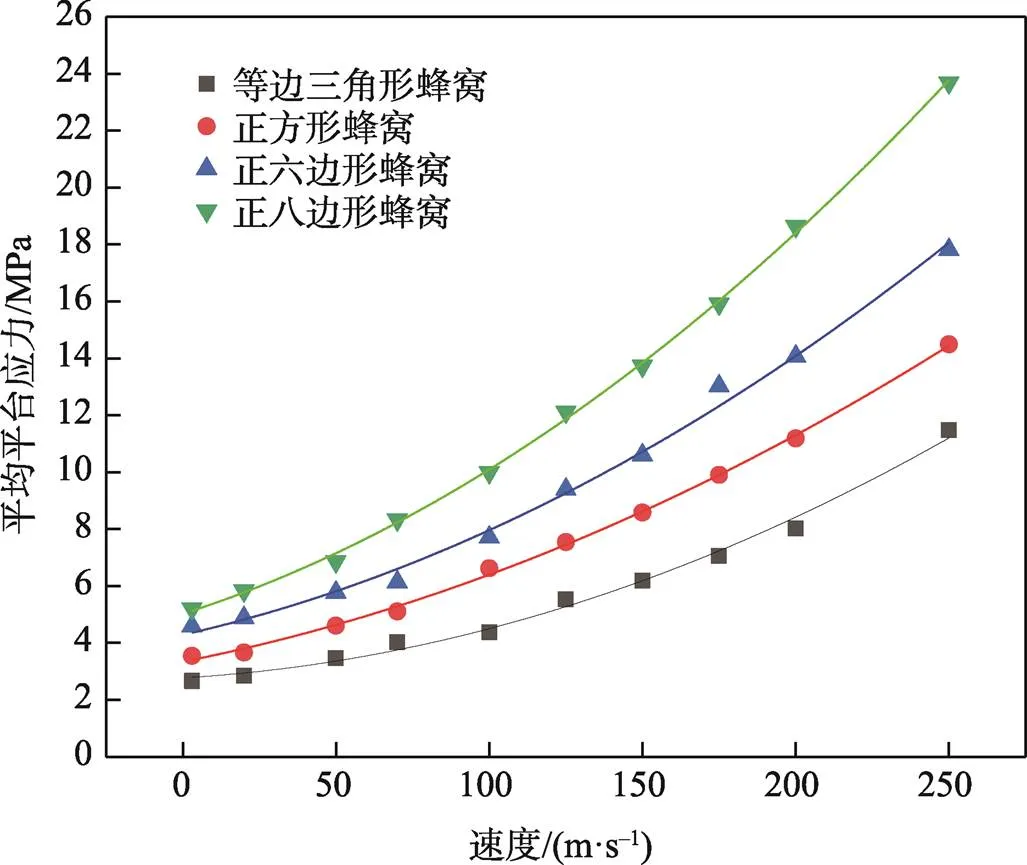
图13 定密度各正多边形蜂窝异面sm-v曲线

分析可得，最佳比能量吸收和冲击速度的关系，可以用二次多项式函数曲线进行拟合（图14），见式（10）。

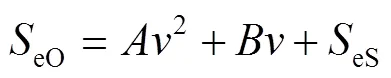
式中，A、B为蜂窝比能量吸收与速度的相关系数；SeS为蜂窝的静态比能量吸收。利用最小二乘法拟合，可以得到各系数值。

4.4 冲击力效率

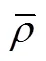
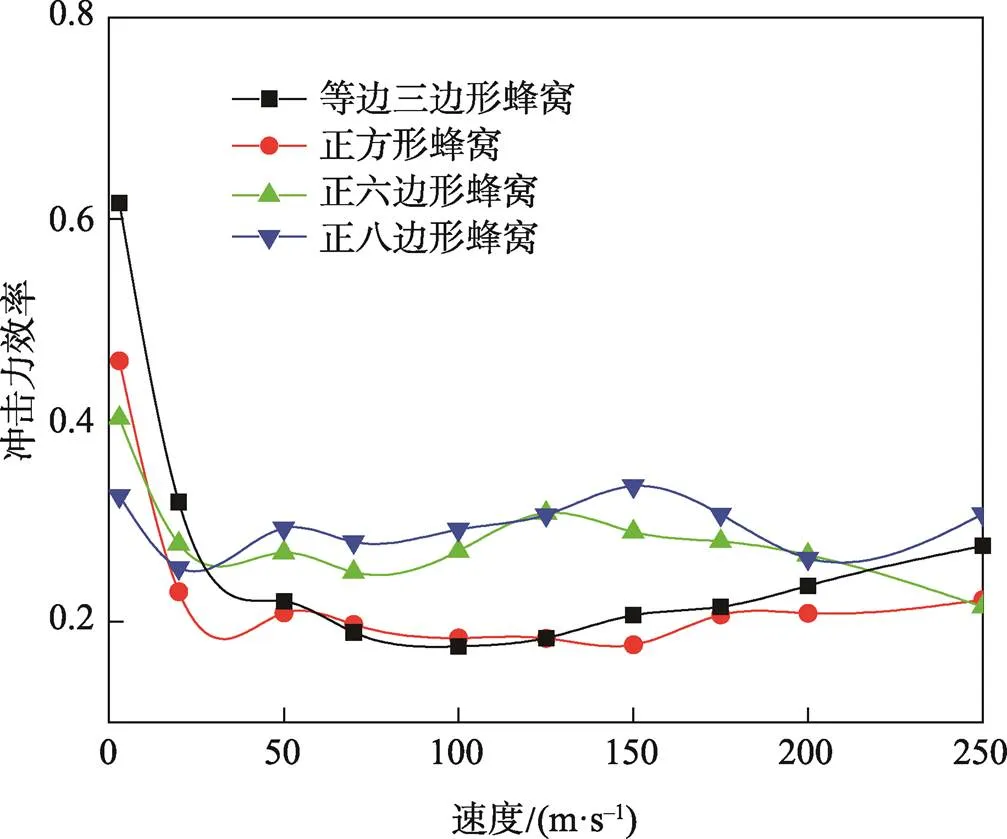
图15 定密度各正多边形蜂窝异面Fe-v曲线(=0.02)

5 结语

本文研究了4种正多边形蜂窝的异面力学性能和能量吸收特性，相关结论有：

1）各蜂窝异面变形模式受构型、冲击速度和相对密度的影响，冲击速度影响显著。

2）提出了最佳应变的概念，它直接影响到各构型蜂窝异面缓冲性能评价，给出了求最佳应变的方法。

3）相对密度相同时，各构型蜂窝在异面冲击过程中应力-应变曲线形态基本一致，均包括线弹性阶段、屈服阶段、平台阶段和密实化阶段，正八边形蜂窝的异面平均平台应力最大。

4）通过最小二乘法得到不同构型蜂窝的异面最佳比能量吸收与冲击速度成二次函数关系，并给出了经验公式。相对密度相同时，正六边形和正八边形的冲击力效率更大。

[1] GIBSON L J, ASHBY M F. Cellular Solids: Structures and Properties, Second Edition[M]. Cambridge: Cambridge University Press, 1997.

[2] 宫晓博, 刘宇鸿, 于昌利, 等. 不同泊松比蜂窝结构抗冲击性能数值分析[J]. 中国舰船研究, 2023, 18(2): 38-47.

GONG Xiao-bo, LIU Yu-hong, YU Chang-li, et al. Numerical Analysis of Impact Resistance of Honeycomb Structures with Different Poisson's Ratios[J]. Chinese Journal of Ship Research, 2023, 18(2): 38-47.

[3] 张豪, 常白雪, 赵凯，等. 三种蜂窝夹芯板的抗爆性能分析[J]. 北京理工大学学报, 2022, 42(6): 557-566.

ZHANG Hao, CHANG Bai-xue, ZHAO Kai, et al. Anti-Explosion Analysis of Honeycomb Sandwich Panels with Three Kinds of Core Structures[J]. Transactions of Beijing Institute of Technology, 2022, 42(6): 557-566.

[4] 白临奇, 史小全, 刘宏瑞，等. 冲击载荷下箭头型负泊松比蜂窝结构动态吸能性能研究[J]. 振动与冲击, 2021, 40(11): 70-77.

BAI Lin-qi, SHI Xiao-quan, LIU Hong-rui, et al. Dynamic Energy Absorption Performance of Arrow Type Honeycomb Structure with Negative Poisson's Ratio under Impact Load[J]. Journal of Vibration and Shock, 2021, 40(11): 70-77.

[5] XU Wen-long, WANG Cheng, LIU Bao-hua, et al. Crushing Responses and Energy Absorption of Bionic Inspired Corrugated Honeycombs[J]. International Journal of Impact Engineering, 2023, 179: 104641.

[6] HE Ruo-huan, ZHAO Cai-qi, GANG Wang, et al. FEA of in-Plane Compression of Aluminum Alloy Honeycomb Panels[J]. Structures, 2023, 49: 267-280.

[7] WANG Shun, LIU Hai-Tao. Energy Absorption Performance of the Auxetic Arc-Curved Honeycomb with Thickness and Arc Angle Gradient Based on Additive Manufacturing[J]. Materials Today Communications, 2019, 35: 105515.

[8] CHEN He-yu, LIU Xin-yang, ZHANG Yu-long, et al. Numerical Investigation of the Compressive Behavior of 2.5D Woven Carbon-Fiber (2.5D-CFRP) Honeycomb and Experimental Validation[J]. Composite Structures, 2023, 312: 116858

[9] WANG Wei-Jing, ZHANG Wei-Ming, GUO Meng-Fu, et al. Energy Absorption Characteristics of a Lightweight Auxetic Honeycomb under Low-Velocity Impact Loading[J]. Thin-Walled Structures, 2023, 185: 110577.

[10] HAN Jia-mian, CHEN He-ming, XU Xiang-yang, et al. Mechanical Characterization of a Novel Gradient Thinning Triangular Honeycomb[J]. Thin-Walled Structures, 2023, 188: 110862.

[11] WU Jian-qin, CHEN Xie, ZHU Heng-yi, et al. Meta-Honeycomb Sandwich Tubes: Designing, Manufacturing, and Crashworthiness Performance[J]. Composites Science and Technology, 2023, 240: 110096.

[12] XUE Zhen-yu, HUTCHINSON J W. Crush Dynamics of Square Honeycomb Sandwich Cores[J]. International Journal for Numerical Methods in Engineering, 2006, 65(13): 2221-2245.

[13] ZHANG Xiong, ZHANG Hui. Numerical and Theoretical Studies on Energy Absorption of Three-Panel Angle Elements[J]. International Journal of Impact Engineering, 2012, 46: 23-40.

[14] 孙德强, 孙玉瑾, 李国志, 等. 不同冲击速度下蜂窝材料耐撞性能的测定方法: 中国, 110849750B[P]. 2022-04-01.

SUN De-qiang, SUN Yu-jin, LI Guo-zhi, et al. Method for Measuring Collision Resistance of Honeycomb Material at Different Impact Speeds: China, 110849750B[P]. 2022-04-01..

Influence of Configuration on Out-of-plane Cushioning Performance of Regular Polygonal Honeycombs

GUAN Tian-jin1, SUN Yu-jin2, SUN De-qiang2*, DU Qiang-qiang2, LUO Ze-long2, LI Jin-tang2

(1. Shenzhen Longteng Printing Technology Service Co., Ltd., Guangdong Shenzhen 518000, China; 2. a. College of Bioresources Chemical and Materials Engineering, b. National Demonstration Center for Experimental Light Chemistry Engineering Education, c. 3S Research Institute of Novel Packaging Science and Technology, Shaanxi University of Science and Technology, Xi'an 710021, China)

The work aims tostudy the cushioning performance of regular polygonal (equilateral triangular, square, regular hexagonal and regular octagonal) honeycombs with the elastic linear strain-hardening (bilinear) isotropic base material under out-of-plane impact through the finite element method. Finite element models based on the regular polygonal honeycomb cells were established for their out-of-plane impact analysis. Based on the proposed new evaluation indicator of most appropriate strain, all cushioning performance evaluation indicators were redefined to form a novel cushioning performance evaluation method. Their deformation modes, stress strain curves, and some cushioning performance evaluation indicators such as mean plateau stress, specific energy absorption and impact force efficiency of regular polygonal honeycombs with different relative densities under different impact velocities were obtained and analyzed. The regular octagonal honeycomb has the maximum mean plateau stress for a given relative density. The specific energy absorption of each regular polygonal honeycomb relies on the impact velocity in a quadratic polynomial curve. The regular hexagonal and octagonal honeycombs with same relative densities outperform equilateral triangular and square honeycombs in impact force efficiency.

regular polygonal honeycombs; most appropriate strain; deformation mode; mean plateau stress; optimal specific energy absorption; impact force efficiency

TB484

A

1001-3563(2023)23-0283-10

10.19554/j.cnki.1001-3563.2023.23.034

2023-07-28

国家自然科学基金（51575327）

责任编辑：曾钰婵