M型预制袋袋口折合机构运动精度可靠性优化

王婧月，陆佳平*，王利强,2

M型预制袋袋口折合机构运动精度可靠性优化

王婧月1，陆佳平1*，王利强1,2

（1.江南大学，江苏 无锡 214122； 2.江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122）

为提高M型预制袋包装机袋口折合机构轨迹输出点的运动精度，对袋口折合机构进行运动精度可靠性优化。在运动学分析的基础上，用环路增量法建立考虑杆长误差时袋口折合机构的位置误差模型，接着对轨迹输出点进行可靠性分析及蒙特卡洛法验证，通过灵敏度分析确定关键误差影响因素，最后进行运动精度可靠性优化。建立的可靠性模型可以有效地反映杆长误差对机构运动精度的影响，分量轨迹的可靠度由82.5%提高至92.91%，分量轨迹可靠度由65.34%提高至89%。经过可靠性优化能够使袋口折合机构运动精度满足设计要求。

包装机械；M型预制袋；袋口折合机构；运动精度；灵敏度；可靠性优化

M型预制袋是一种工业上常用的柔性包装容器，它是由筒状薄膜经支撑板撑起四周，插边轮将薄膜侧面沿着中线折入，使左右两侧面折成M字形制成的。M型预制袋在经过充填后，形成了自由开放袋口，需要用折合机构对袋口进行折合，使得M型预制袋按预定边要求再次折叠完成袋口的闭合。但由于机构轨迹输出点的运动精度将直接影响M型预制袋袋口折合工序的可靠性，且多连杆机构的运动误差具有累积效应，所以有必要探究无法消除的随机误差对M型预制袋袋口折合机构运动精度的影响。

平面连杆机构的随机误差主要有构件的尺寸误差、运动副的间隙、运动副轴线的歪斜等[1]。目前国内外学者已经对可靠性问题进行了大量的研究，并取得了丰硕的成果[2-6]。然而，这些可靠性的相关理论却较少运用于包装机械领域[7-11]。

针对M型预制袋在折合工序时对袋口折合机构轨迹输出点的高精度要求以及目前包装机械领域在运动精度可靠性方面研究的不足，基于环路增量法建立考虑杆长尺寸误差时的运动误差模型。在此基础上分析了袋口折合机构的点位置可靠度以及轨迹可靠度，并用蒙特卡洛方法进行验证，通过灵敏度分析模型讨论各杆件制造误差标准差对机构运动精度的影响程度，并找到影响机构运动精度的关键因素。最后综合灵敏度信息和成本进行袋口折合机构可靠性优化。

1 M型预制袋袋口折合机构运动学分析

袋口折合机构对称分布于M型预制袋的两侧，单侧机构的运动简图如图1所示。该机构由哈特第二连杆机构演化，含有8杆10副，自由度为1。其中3副构件杆4和杆2的夹角以及固接在一起的杆、之间的夹角均为定值180°。在理想条件下由主动构件杆1带动，可以使、、3点分别沿轴负方向、轴负方向、轴正方向作精确直线运动（即x=y=x=0），从而实现M型预制袋袋口的折合。

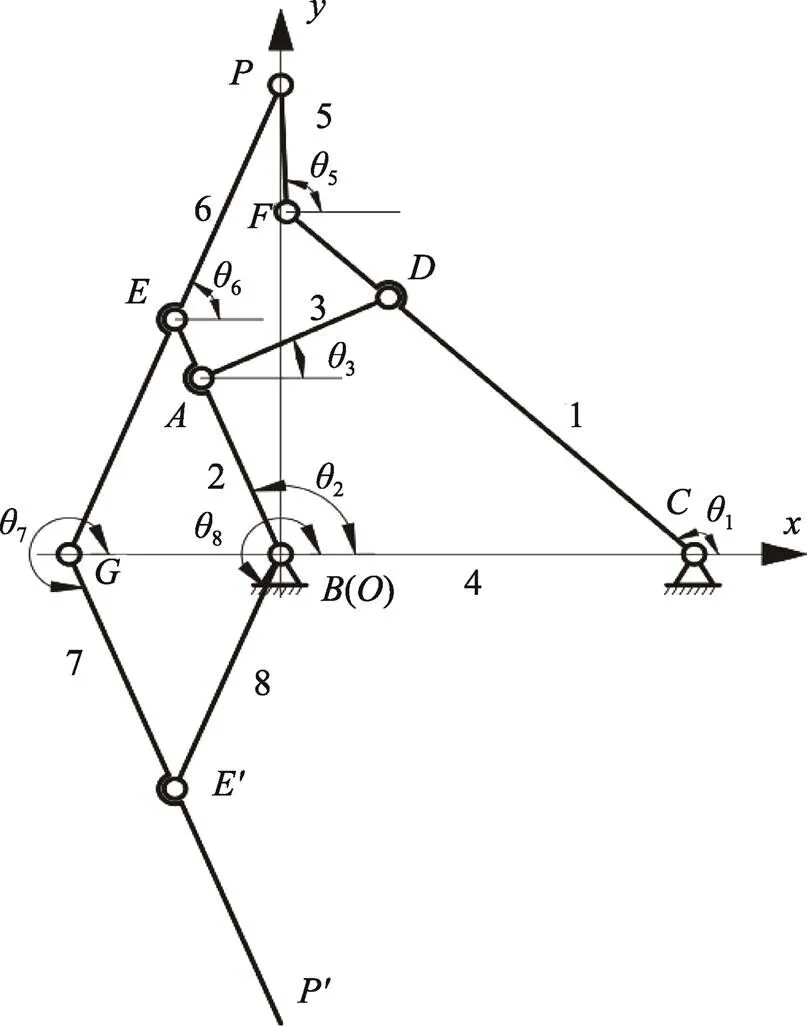
图1 M型预制袋袋口折合机构运动简图

综上所述轨迹输出点、、3点的运动精度将直接影响M型预制袋袋口折合工序的可靠性，但根据多连杆机构误差累积作用，以运动误差最大的点进行运动精度可靠性分析。根据3个环路的矢量封闭方程，建立机构运动方程式（1）。

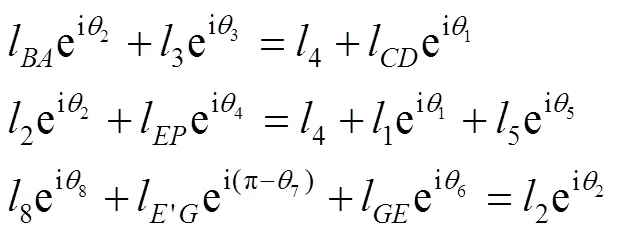
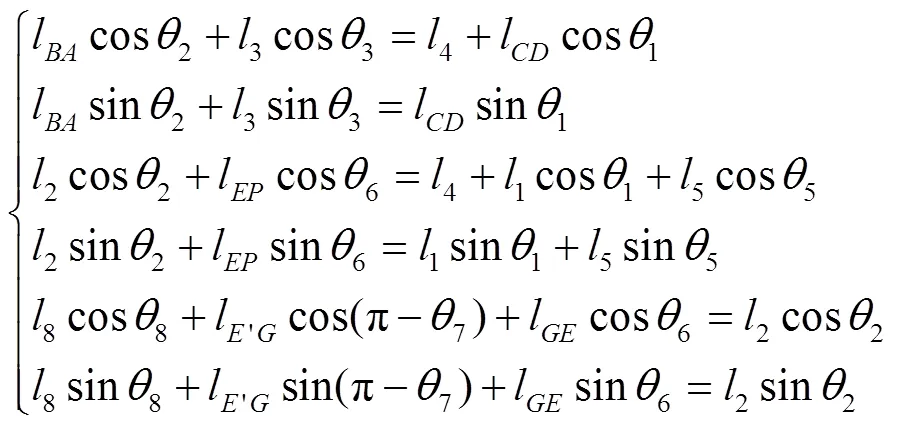
在直角坐标系下，轨迹输出点的坐标值可以写为

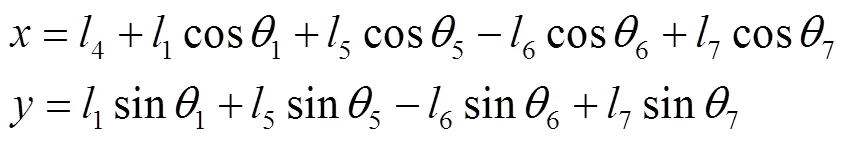
2 袋口折合机构点位置可靠性分析

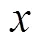
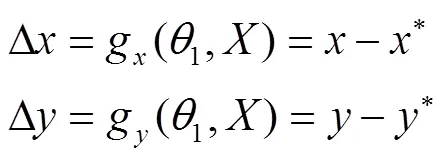
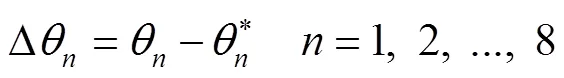
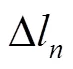
2.1 考虑杆长尺寸误差的运动误差模型

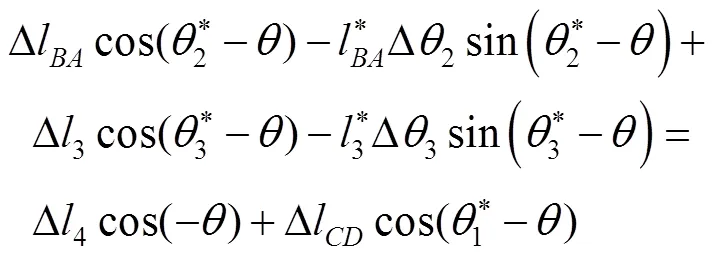
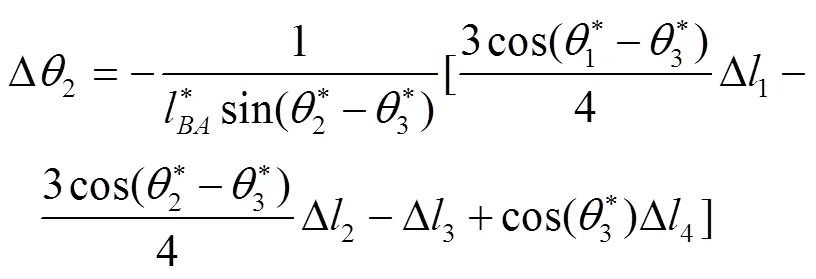
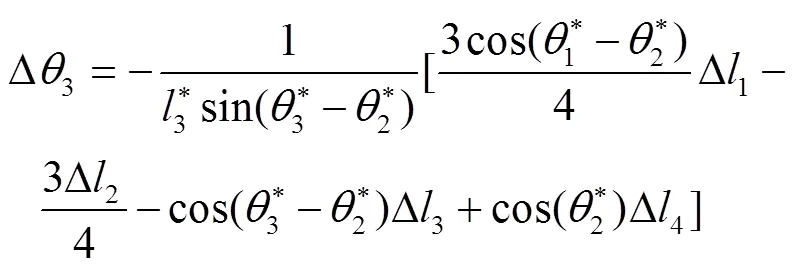
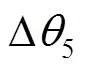
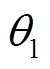
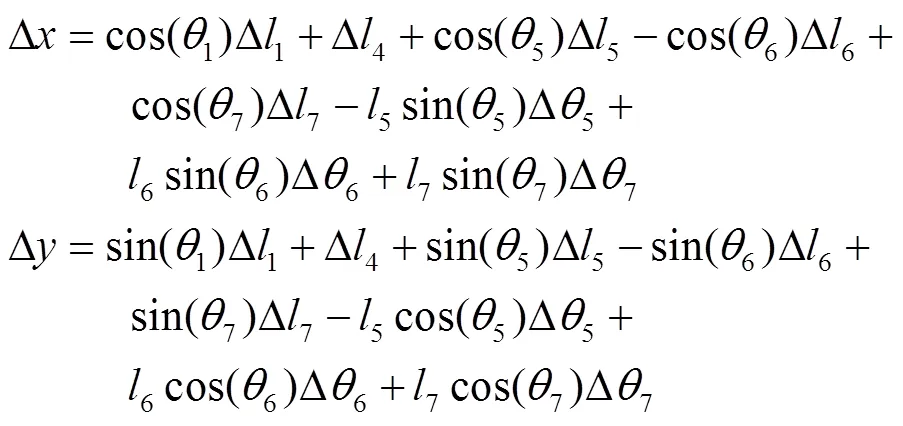
2.2 机构点位置可靠度模型

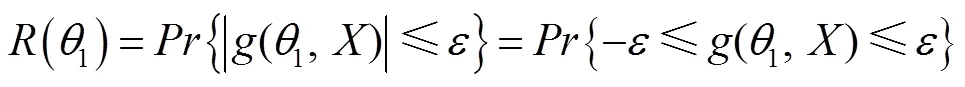
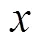
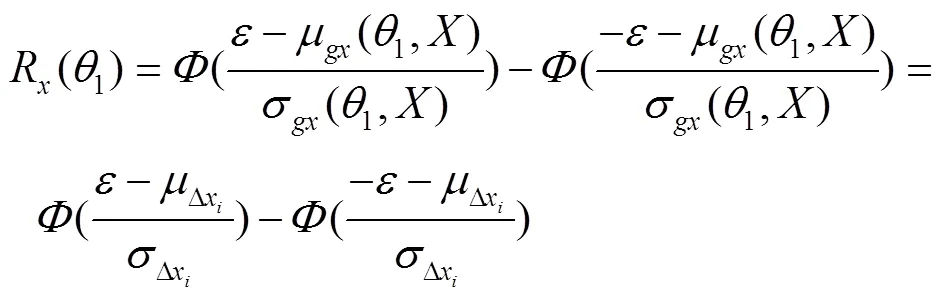
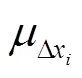
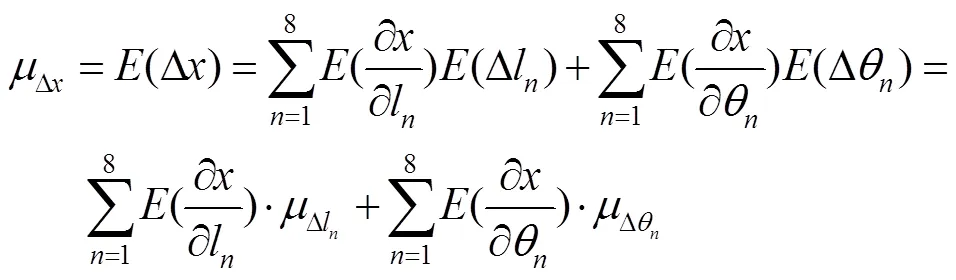
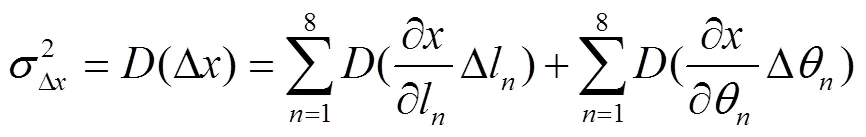
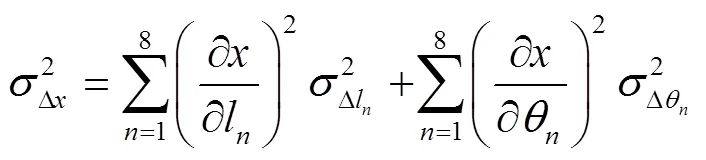
2.3 机构轨迹可靠度模型

2.2节建立的是机构点位置的可靠性模型，反映了机构在运动过程中各随机误差瞬时对轨迹输出点的运动精度的影响。但是无法综合反映各随机误差对整条轨迹的影响，显然分析轨迹可靠性更具有实用价值，因此有必要建立机构轨迹精度可靠性模型[13]。

设驱动构件的转角1的工作区间为[0,θ]，机构存在个轨迹点，且每个轨迹点对应的驱动构件转角为θ，可以建立点在和方向运动分量的轨迹可靠度为：

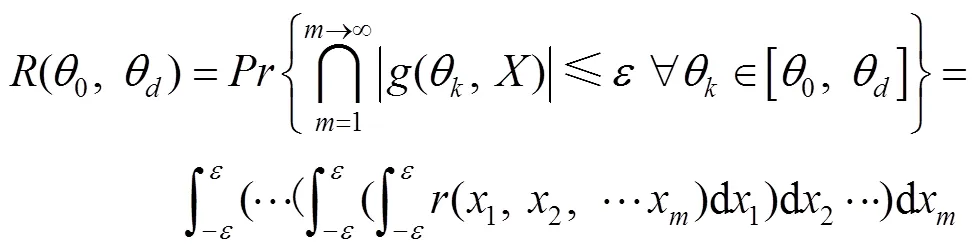
式（15）的概率密度函数难以求解，涉及到多维积分的计算，且当选取的轨迹点数目多时非常困难。为了简化运算，引入等效极值[37]的思想，式（15）可简化为：

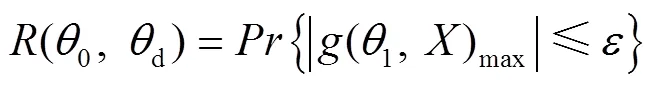
2.4 MATLAB仿真和结果分析

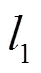
结合上述方法，运用Matlab软件进行数学仿真。另外，为了验证上述模型的有效性，在驱动构件的转角工作范围内取121个点，用蒙塔卡洛方法模拟104次，计算考虑杆长误差时点各分量的轨迹可靠度。

仿真结果如表1所示，计算结果表明点各分量的点位置可靠度的最小值均在驱动构件转角为177°时。由表1可知，用蒙特卡洛方法计算的轨迹精确度与所建模型误差较小，验证了所建模型的有效性；杆长尺寸误差对点轴方向运动精度的影响不容小觑；目前初选的公差无法满足袋口折合机构的运动精度要求，后续有必要重新对杆长尺寸公差进行精度分配，以提高机构运动精度可靠性。

表1点各分量的轨迹可靠度

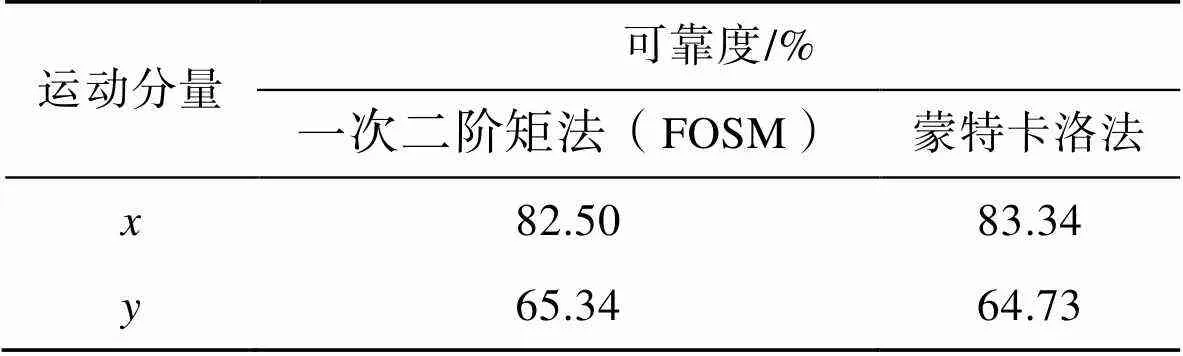
Tab.1 Track reliability of each component of point P'

3 基于灵敏度信息的关键影响因素识别

3.1 袋口折合机构灵敏度分析

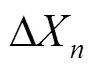
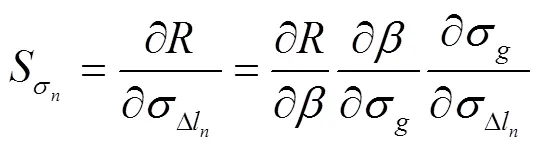
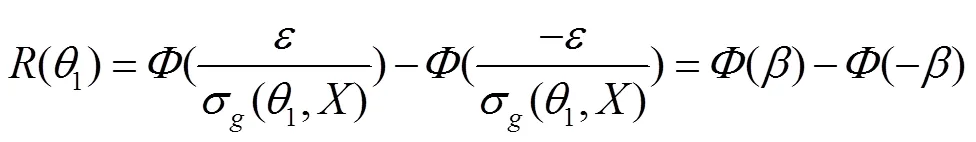
将式（18）代入式（17）得：

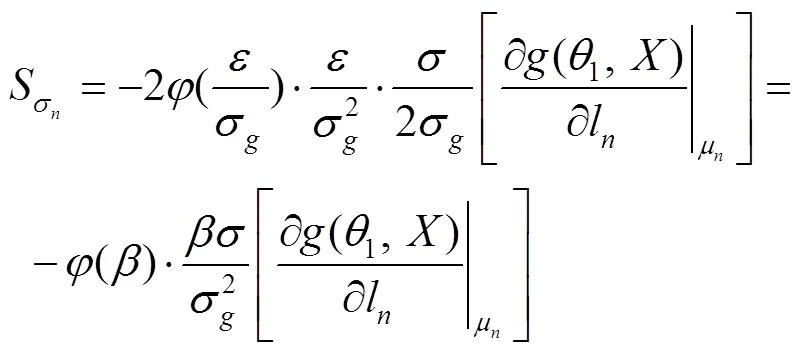
式中：( )为标准正态分布的概率密度函数。

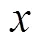
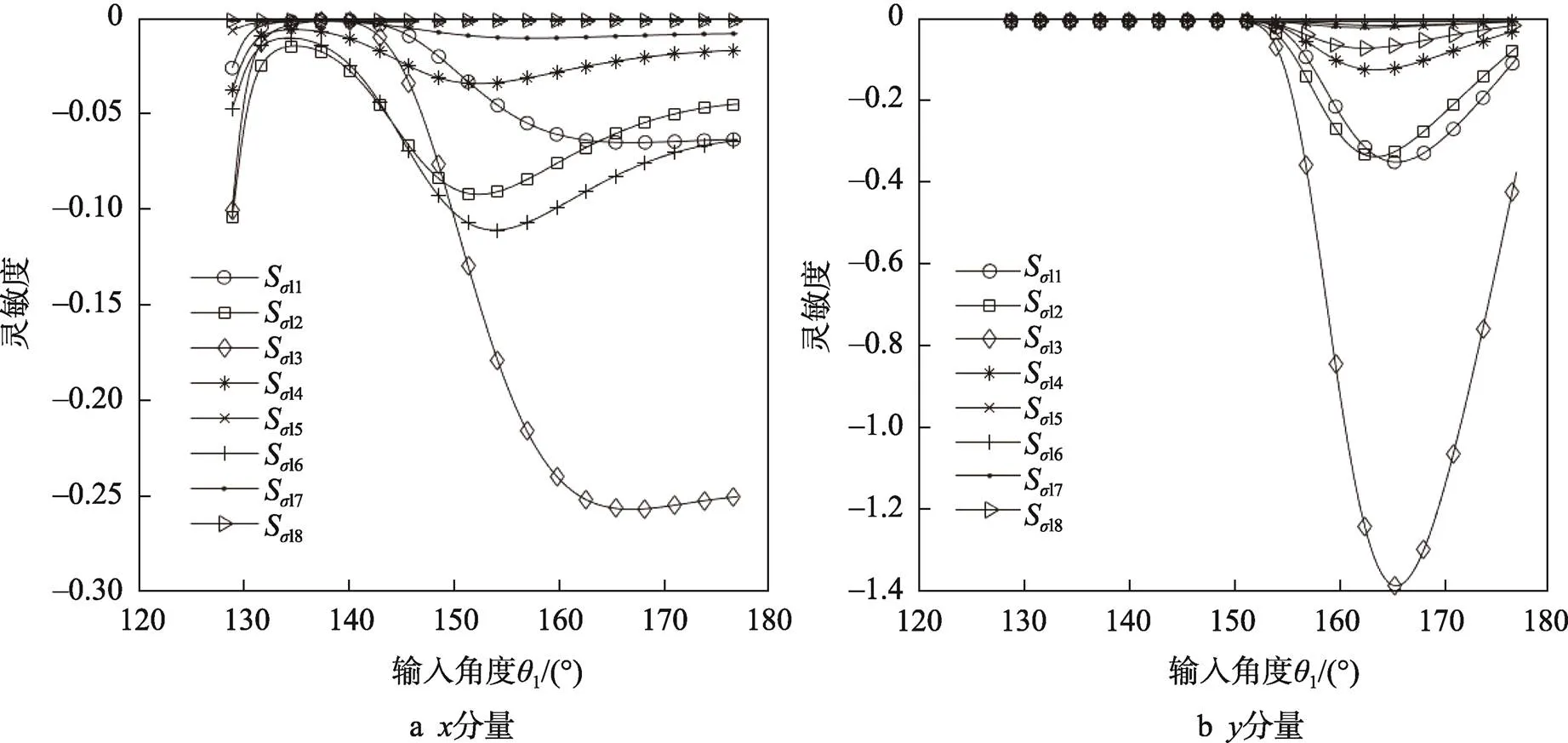
图2 标准差对P'点可靠性的灵敏度

3.2 关键误差影响因素识别

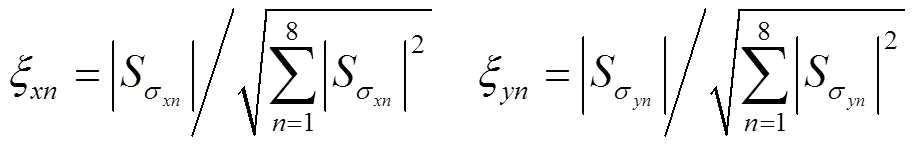
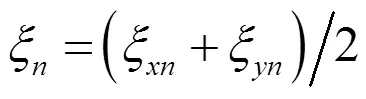
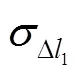
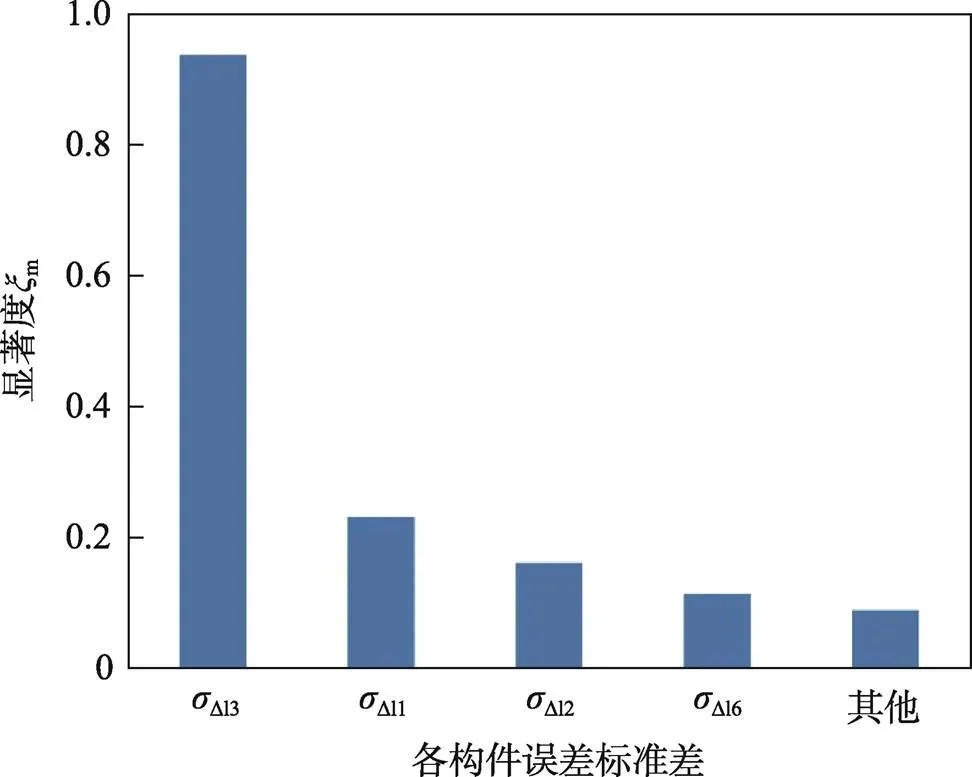
图3 关键误差因素对位置误差的综合显著度

4 袋口折合机构可靠性优化

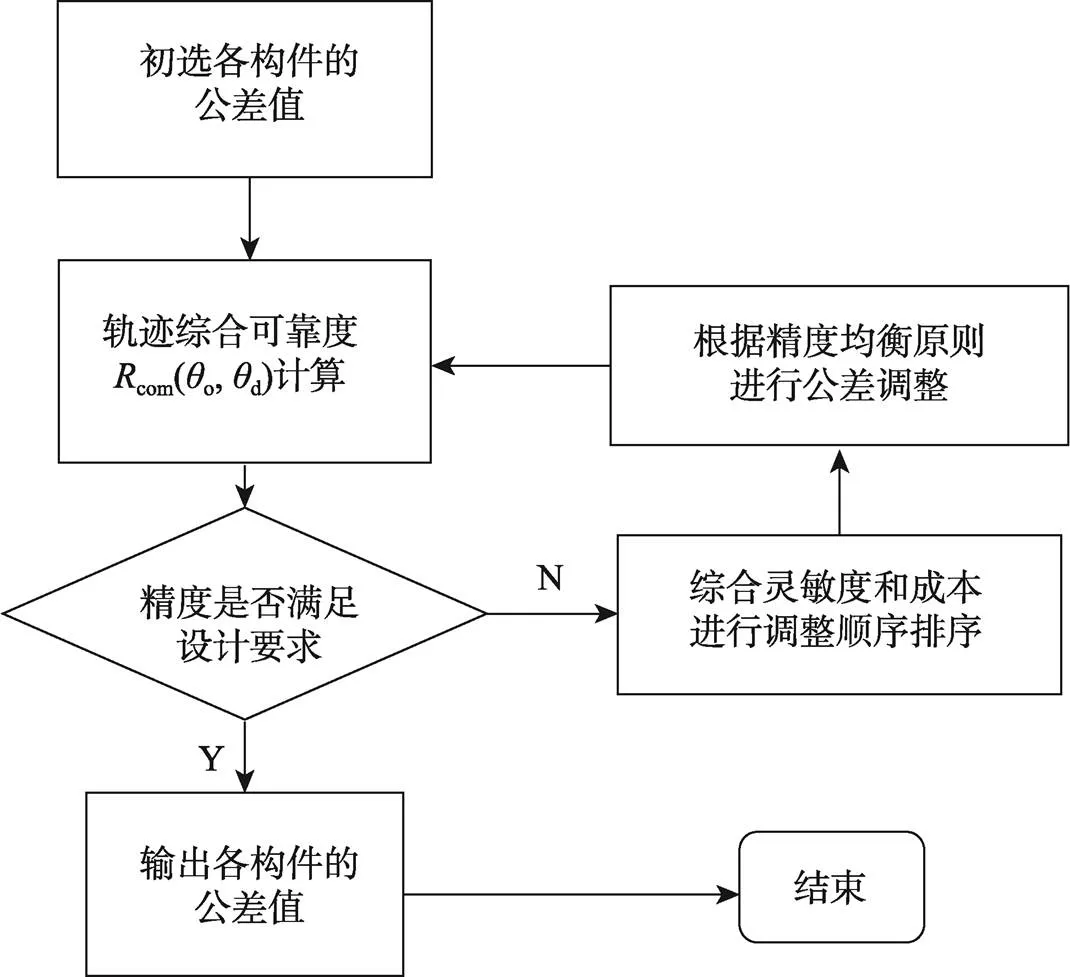
图4 基于灵敏度信息的机构精度综合流程

4.1 各误差因素公差调整顺序的确定

以最大显著度的误差因素杆3为基准求出各构件的灵敏度综合系数R=3/n，如式（22）所示。R的数值意义为运动精度的相对影响程度，其值越小，表示在所有因素中影响越显著，公差调整时越应该优先考虑。

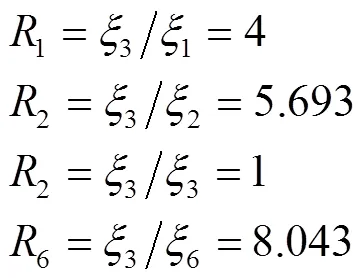
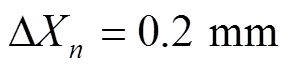
加权方法在解决只有2个目标函数的优化问题方面非常有效，因此使用加权方法综合考虑灵敏度综合系数R和成本综合系数K得到加权线性组合系数M[16]，见式（23）。

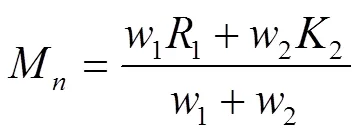
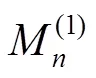
表2 综合灵敏度和成本的加权线性组合系数

Tab.2 Weighted linear combination coefficient that combines sensitivity and cost

4.2 公差调整过程及最终结果

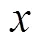
表3 调整过程和调整结果

Tab.3 Adjustment process and results

5 结语

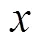
[1] 石则昌, 刘深厚. 机构精确度[M]. 北京: 高等教育出版社, 1995: 1.

SHI Ze-chang, LIU Shen-hou. Mechanism Accuracy[M]. Beijing: Higher Education Press, 1995: 1.

[2] SHI Z. Synthesis of Mechanical Error in Spatial Linkages Based on Reliability Concept[J]. Mechanism and Machine Theory, 1997, 32(2): 255-259.

[3] KIM J, SONG W J, KANG B S. Stochastic Approach to Kinematic Reliability of Open-Loop Mechanism with Dimensional Tolerance[J]. Applied Mathematical Modelling, 2010, 34(5): 1225-1237.

[4] DU Xiao-ping. Time-Dependent Mechanism Reliability Analysis with Envelope Functions and First-Order Approximation[J]. Journal of Mechanical Design, 2014, 136: 1-4.

[5] 吴吉平, 贺兵, 胡威林. 直线运动机构轨迹可靠性灵敏度分析[J]. 机械传动, 2016, 40(6): 140-143.

WU Ji-ping, HE Bing, HU Wei-lin. Sensitivity Analysis of Trajectory Reliability of Linear Motion Mechanism[J]. Journal of Mechanical Transmission, 2016, 40(6): 140-143.

[6] 聂飞飞, 周金宇, 曹清林. 高速经编机槽针机构运动精度可靠性优化[J]. 机械设计与制造, 2019(12): 40-44.

NIE Fei-fei, ZHOU Jin-yu, CAO Qing-lin. The Optimization of Kinematics Accuracy Reliability on Needle Mechanism of High-Speed Warp Knitting Machine[J]. Machinery Design & Manufacture, 2019(12): 40-44.

[7] 余成发, 王勇. 全自动模切机清废机构运动精度可靠性分析[J]. 包装工程, 2009, 30(3): 3-6.

YU Cheng-fa, WANG Yong. Reliability Analysis for Kinematics Accuracy of Trash-Cleaning Mechanism of Automatic Die Cutting Machine[J]. Packaging Engineering, 2009, 30(3): 3-6.

[8] 刘志青. 药品包装盒出盒机构设计与运动精度可靠性分析[D]. 湘潭: 湘潭大学, 2020: 13-18.

LIU Zhi-qing. Analysis of the Design of the Mechanism and the Reliability of the Motion Accuracy of the Medicine Packing Box[D]. Xiangtan: Xiangtan University, 2020: 13-18.

[9] 郎诗慧, 辛洪兵. 糖果包装机推糖机构的运动精度分析[J]. 包装工程, 2017, 38(5): 49-57.

LANG Shi-hui, XIN Hong-bing. Kinematic Accuracy of Candy Pusher of Candy Packaging Machine[J]. Packaging Engineering, 2017, 38(5): 49-57.

[10] 吴金文, 田祎. 推料四杆机构参数优化与运动精度分析研究[J]. 包装工程, 2018, 39(21): 163-167.

WU Jin-wen, TIAN Yi. Research on Parameter Optimization and Motion Accuracy Analysis of Pushing Four-Bar Mechanism[J]. Packaging Engineering, 2018, 39(21): 163-167.

[11] 赵之瑜. 糊底机贴阀装置优化设计[D]. 兰州: 兰州交通大学, 2022: 9-13.

ZHAO Zhi-yu. Optimal Design of Valve Sticking Device for Bottom Pasting Machine[D]. Lanzhou: Lanzhou Jiatong University, 2022: 9-13.

[12] 孙志礼, 陈良玉. 实用机械可靠性设计理论与方法[M]. 北京: 科学出版社, 2003: 210-221.

SUN Zhi-li, CHEN Liang-yu. Theory and Method of Practical Mechanical Reliability Design[M]. Beijing: Science Press, 2003: 210-221.

[13] 潘敬锋, 訾斌, 王正雨, 等. 基于试验与仿真联合分析的喷涂机器人轨迹精度可靠性研究[J]. 机械工程学报, 2020, 56(19): 210-220.

PAN Jing-feng, ZI Bin, WANG Zheng-yu, et al. Research on Reliability of Spray Robot Trajectory Accuracy Based on Conjoint Analysis of Experiment and Simulation[J]. Journal of Mechanical Engineering, 2020, 56(19): 210-220.

[14] 龙进, 张均富, 王进戈. 平面四杆转向机构运动可靠性灵敏度分析[J]. 机械设计与研究, 2011, 27(6): 21-23.

LONG Jin, ZHANG Jun-fu, WANG Jin-ge. The Kinematic Reliability Sensitivity Analysis of Planar Four-Bar Steering Mechanism[J]. Machine Design and Research, 2011, 27(6): 21-23.

[15] 刘涛, 文瑞桥, 张均富. 弧面分度凸轮机构的运动可靠性灵敏度分析[J]. 西华大学学报(自然科学版), 2017, 36(3): 36-39.

LIU Tao, WEN Rui-qiao, ZHANG Jun-fu. The Kinematic Reliability Sensitivity Analysis of Globoidal Indexing Cam Mechanism[J]. Journal of Xihua University (Natural Science Edition), 2017, 36(3): 36-39.

[16] 骞华楠, 陶璟, 于随然. 高精度压力机连杆机构的误差分析及精度综合[J]. 上海交通大学学报, 2019, 53(3): 269-275.

QIAN Hua-nan, TAO Jing, YU Sui-ran. Error Analysis and Accuracy Synthesis for Linkage Mechanism of High-Precision Press[J]. Journal of Shanghai Jiao Tong University, 2019, 53(3): 269-275.

Reliability Optimization of Opening Folding Mechanism Movement Accuracy of M-shaped Prefabricated Bags

WANG Jing-yue1, LU Jia-ping1*, WANG Li-qiang1,2

(1. Jiangnan University, Jiangsu Wuxi 214122, China; 2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Jiangsu Wuxi 214122, China)

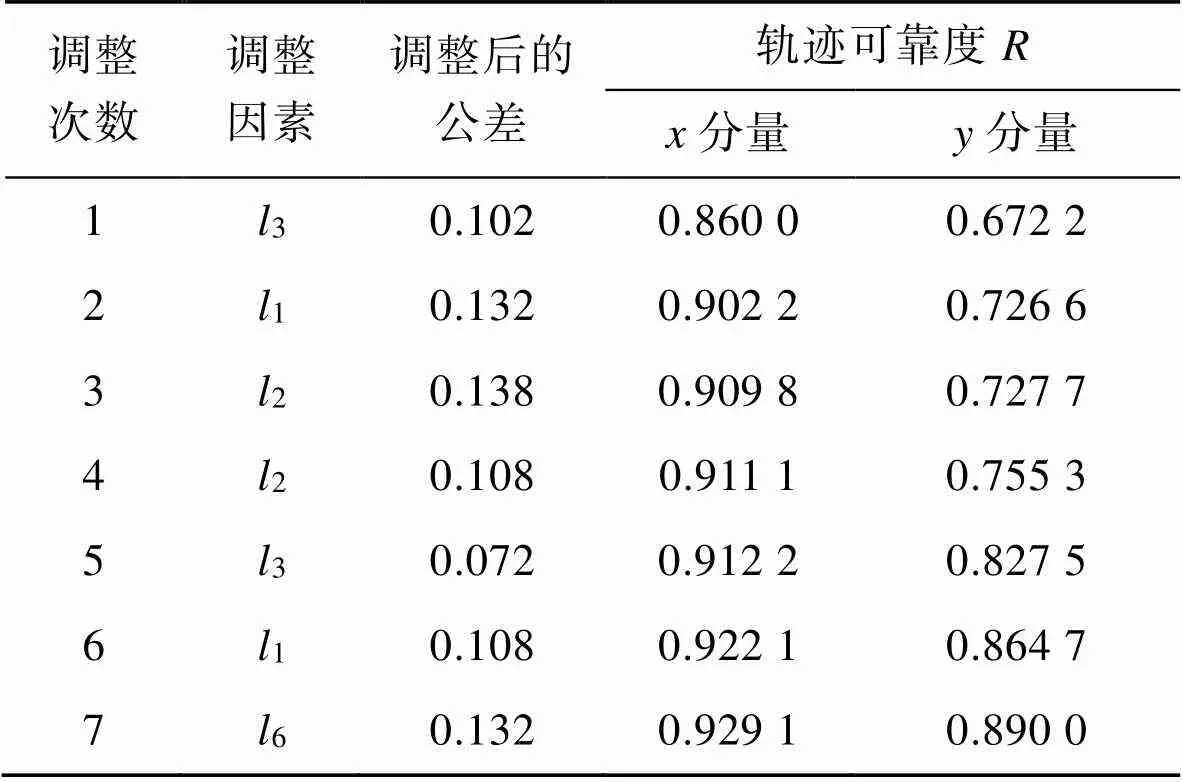
The work aims to improve the kinematic accuracy of the trajectory output point of the M-shaped prefabricated bag opening folding mechanism, and optimize the kinematic accuracy reliability of the opening folding mechanism. Based on kinematic analysis, a position error model of the opening folding mechanism considering rod length errors was established according to the loop increment method. Then, reliability analysis and Monte Carlo verification were performed on the trajectory output points, and key error influencing factors were determined through sensitivity analysis. Finally, reliability optimization of motion accuracy was performed.The results showed that the reliability model established could effectively reflect the impact of rod length errors on the kinematic accuracy of the mechanism. The reliability of the-component trajectory was increased from 82.5% to 92.91%, and the reliability of the-component trajectory was increased from 65.34% to 89%. In summary, the reliability optimization can make the movement accuracy of the opening folding mechanism meet the design requirements.

packaging machinery;M-shaped prefabricated bag; opening folding mechanism; kinematic accuracy; sensitivity; reliability optimization

TH112

A

1001-3563(2023)23-0191-07

10.19554/j.cnki.1001-3563.2023.23.023

2023-03-30

自主研究课题资助项目（FMZ201902）

责任编辑：曾钰婵