基于模糊PID的螺旋加料机构粉体进料精度控制

付海明，黄兴元，邱光军，陈达

基于模糊PID的螺旋加料机构粉体进料精度控制

付海明，黄兴元*，邱光军，陈达

（南昌大学 先进制造学院江西省轻质高强结构材料重点实验室，南京 330031）

螺旋式加料机构存在传感器响应时间差，造成系统延迟，非线性等问题，采用容积式来计量填充物料的质量的填充误差大。本文提出一种基于模糊PID控制的螺旋式加料机构计量控制系统。利用模糊PID对螺杆式粉料加料装置进行控制，通过模糊规则对PID控制比例、积分、微分参数实现参数自调整。基于Matlab中Simulink模块下模拟该模糊PID控制系统。该控制系统稳定时间减少了66%，快速性提高了21%，超调量降低了10%。基于模糊PID控制系统的计量控制性能优于传统PID的。

螺旋式加料机构；计量控制系统；模糊控制；PID控制；MATLAB；Simulink

随着社会经济的发展，粉料包装在食品、日化、化工等行业，特别是近年来食品行业快速发展，食品包装机械的需求越来越大。自动化程度不断变高，对包装精度的要求也越来越高[1-2]。现在中国的定量称重技术比国外还稍有落后[3]，精确地动态称重计量是包装精度的最重要的部分，对现在技术仍然是个难题[4]。工业包装机械控制精度低，包装机械给料装置大多采用螺旋给料装置，单一采用螺旋填充属于容积式来计量填充物料的重量，容积式填充计量依赖于物料密度与填充率稳定，使用开环控制计量精度不够[5]。随着先进控制理论的发展，一些学者对其进行了相关研究：吴宇平等[6]提出基于RBF神经网络PID的定量称重包装控制策略。利用具有任意非线性表达能力及较强自学习能力的RBF神经网络寻求最佳的PID参数，RBF神经网络的PID控制性能明显优于传统PID的。陈静等[7]基于PI控制上，使用模糊控制算法自调整PI参数，控制系统稳定，超调量小，抗干扰能力强。

文中采用基于模糊PID对螺杆式粉料给料装置进行控制，通过模糊规则对PID参数实现参数自调整。首先确定其驱动步进电机86BYG250H的传递函数，利用Matlab中Simulink设计模糊PID控制器，然后通过MATLAB进行仿真。

1 螺旋式加料装置

1.1 螺旋式加料装置的结构

螺旋式加料装置的结构如图1所示

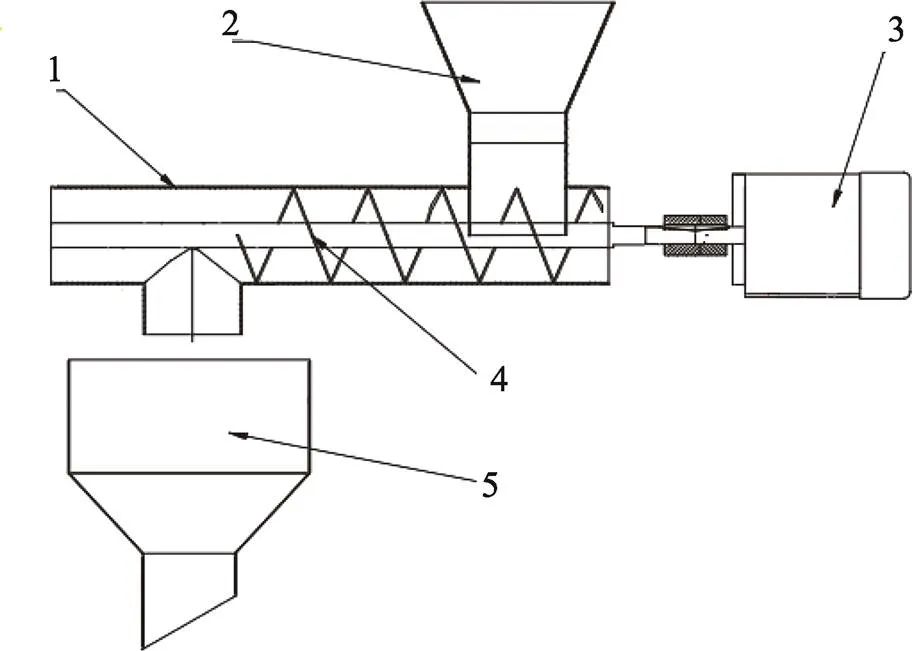
螺旋式加料装置由进料斗、槽体、螺旋叶片和步进电机构成。步进电机驱动螺旋叶片旋转，开始下料，采用快慢进料方式进料，称量10 kg为一袋，在质量相差较大时步进电机转速大；在质量到达9.75 kg时开始模糊PID控制慢进料；当物料到达10 kg时，步进电机停止。等待下次信号再次加料。

1.2 输送量

输送量表示螺旋加料装置单位时间物料密度不变与填充率为100%下粉料输出质量的多少[8]，计算见式（1）。

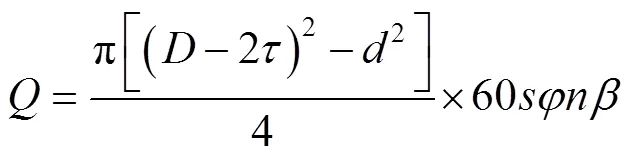
式中：为螺旋加料装置的输送量；为螺旋输送机的叶片直径；为螺旋叶片外径与螺槽内壁最小间隙；为螺旋轴的直径；为螺距；为螺旋填充系数；为螺旋轴的转速；为螺旋输送机的倾斜系数。

由于物料密度与填充率不稳定，容积式来计量填充物料的质量精度不够，本文基于模糊PID对螺杆式粉料给料装置进行控制，过程物料密度与填充率的变化不影响称量精度，并可实现PID参数自调整，结合模糊控制进行控制器设计。

2 步进电机86BYG250H的传递函数

实现螺杆式加料机构粉体进料精度控制需要对其驱动步进电机建立模型。步进电机86BYG250H是两相混合式步进电机，混合式步进电机具有高度非线性，无法对其精确描述，对混合式步进电机做以下简化和假定：近似永磁体产生磁链随转子位置角按正弦规律变化，并假设绕组电感与转子位置无关，忽略两相绕组间互感[9-11]。混合式步进电机A，B相的相电压平衡方程式为：

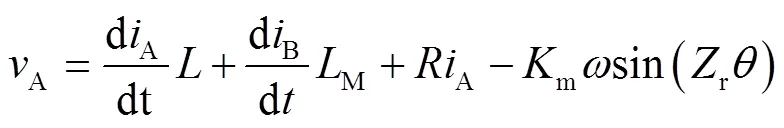
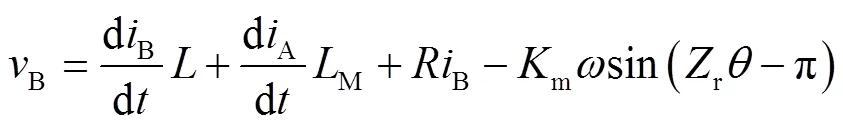
转矩对应的平衡方程为：

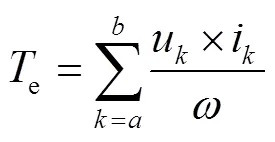
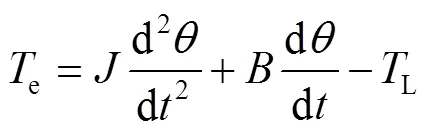
将式（2）～（4）代入式（5）可得：

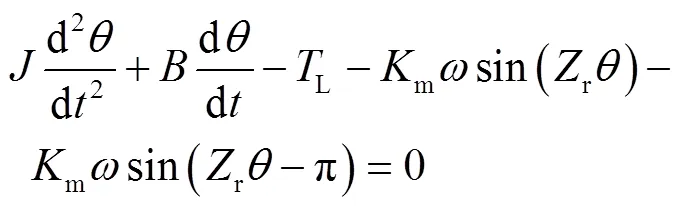
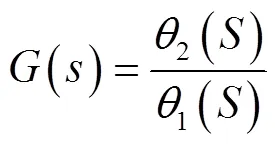
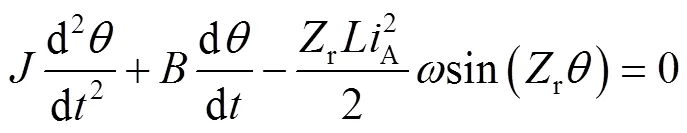
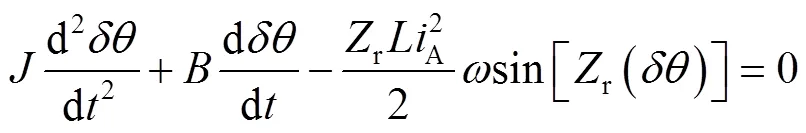
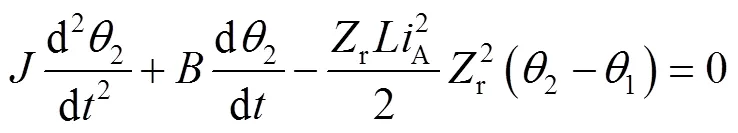
式（10）经过Laplace Transform得：

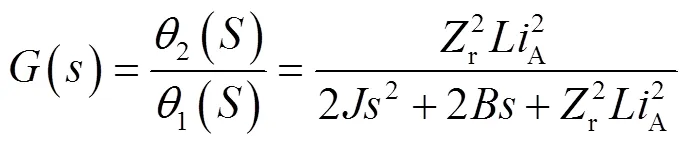
查阅资料得步进电机86BYG250H电机齿数为50、转动惯量为4.57 J/(kg·cm2)、阻尼黏滞系数为0.07、感抗为7.8L/Mh、相电流为6 A、步距角为1.8°。可得步进电机响应函数：

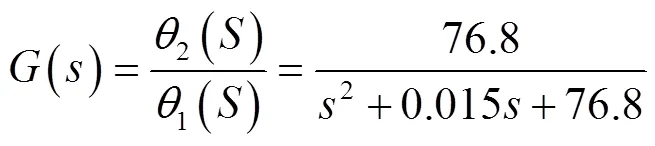
3 模糊PID控制系统

3.1 模糊PID控制器的设计

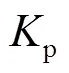
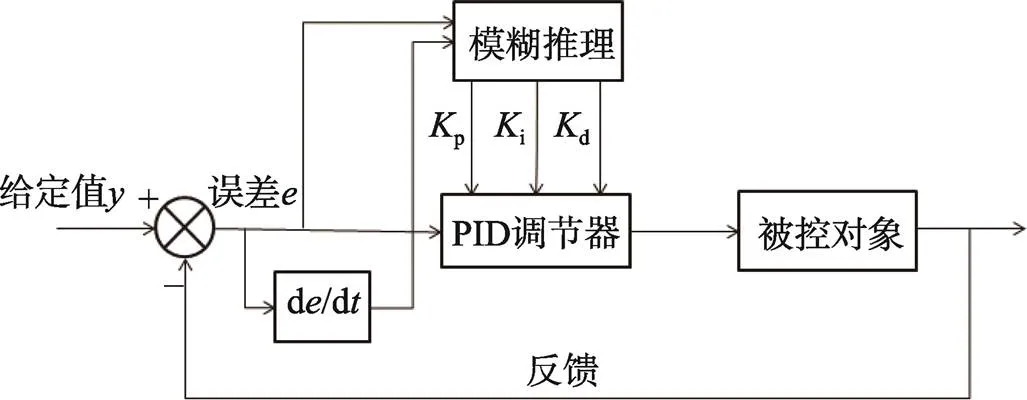
图2 模糊PID控制框图

根据PID参数调整经验，确定模糊控制器的模糊控制规则表。先经过模糊化、模糊控制规则进行模糊推理和去模糊化，得到Δp、Δi、Δd参数。对参数p、i、d进行实时调整，模糊PID参数初始值为po、io、do。与PID控制中p、i、d一样，通过试凑法将po、io、do对应的初始值分别取2.5、15、0.99。Δp、Δi、Δd是模糊PID控制器对应参数调整量[14-15]，得出整定后的模糊PID参数为：

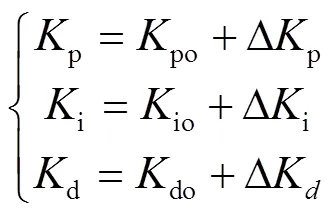
3.2 输入输出变量的确实

3.3 隶属度函数的选择

考虑论域的覆盖程度及灵敏度、稳定性和鲁棒性等原则，同时为了协调参数调整，各模糊子集以三角形及S型函数为隶属度函数曲线。系统的隶属度函数选择三角形函数[16]，隶属度函数如图3～7所示。

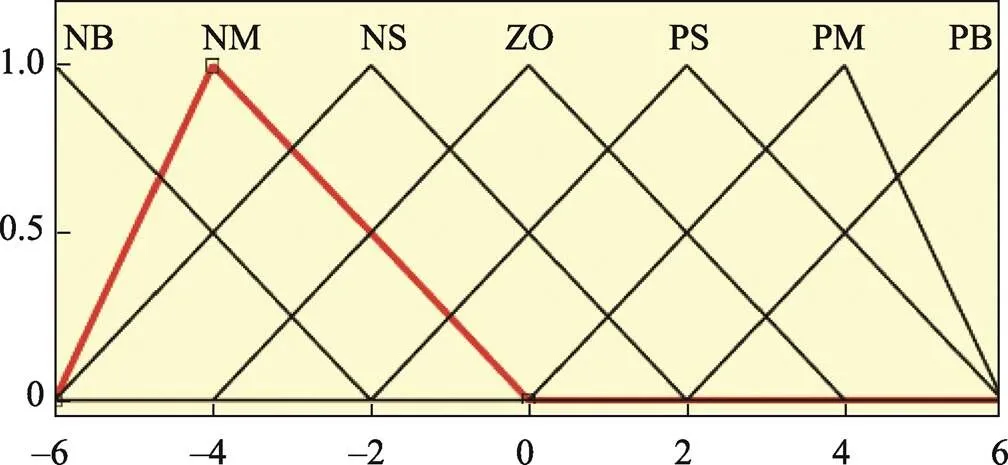
图3 偏差E隶属度函数

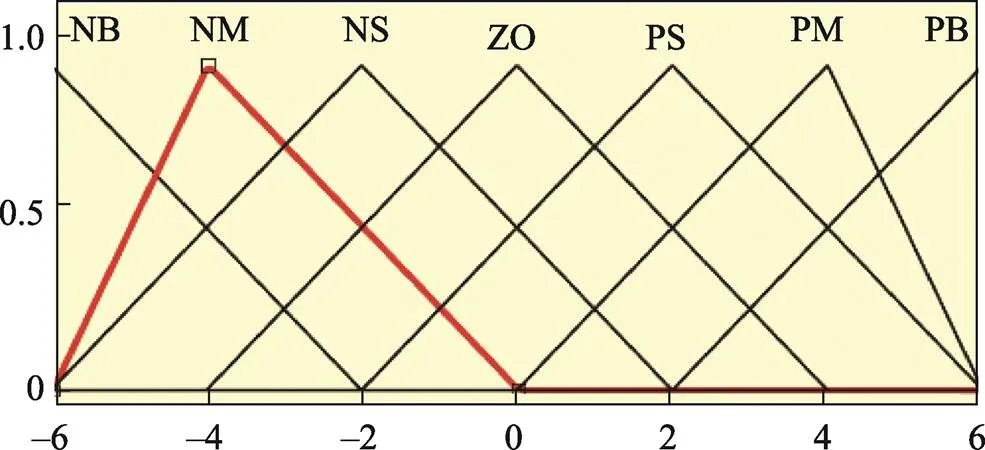
图4 偏差变化率EC隶属度函数

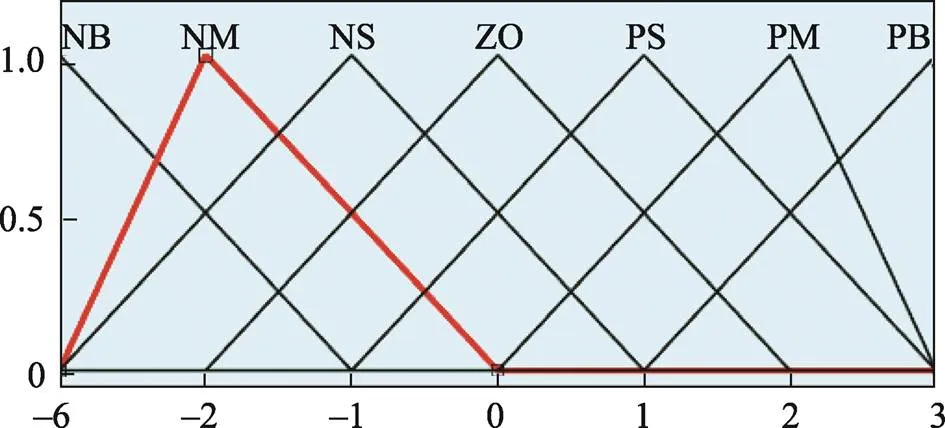
图5 Kp隶属度函数

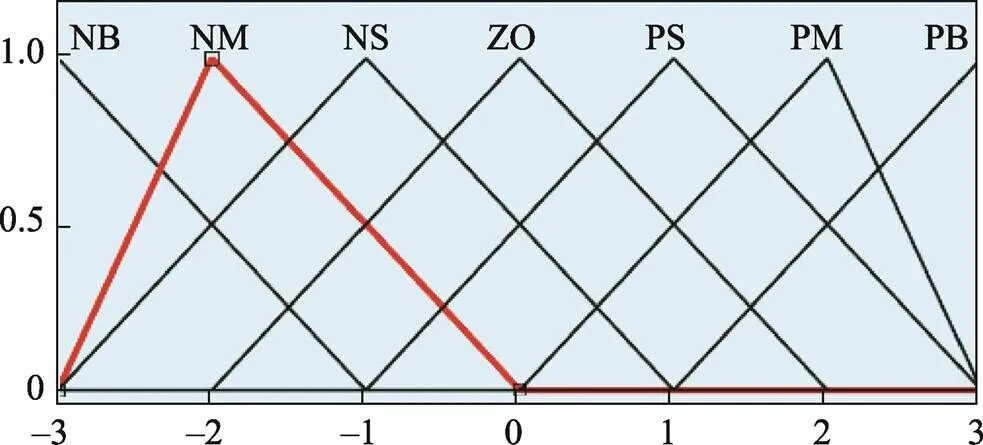
图6 Ki隶属度函数

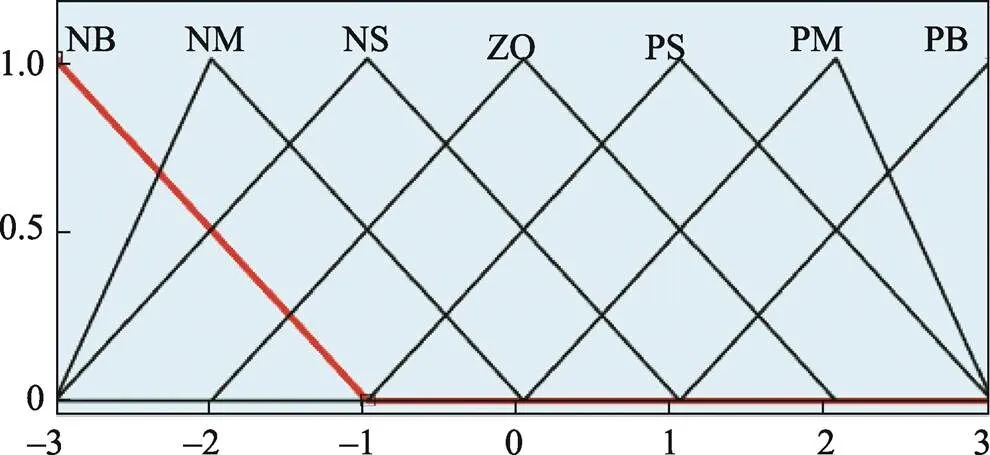
图7 Kd隶属度函数

3.4 模糊控制规则的确定

模糊控制规则库设计就是利用工人熟练操作的经验和语言表达专家的知识，按照人的思维方式制定模糊控制规则的过程。去模糊化的方法有多种，本文控制系统选用重心法去模糊化，对输入空间论域的所有组合计算出相应的输出控制量，从而得到所需的模糊控制器的控制表[17]。根据操作经验和实验分析获得推理规则如表2～4所示。

表1 Δp模糊规则控制

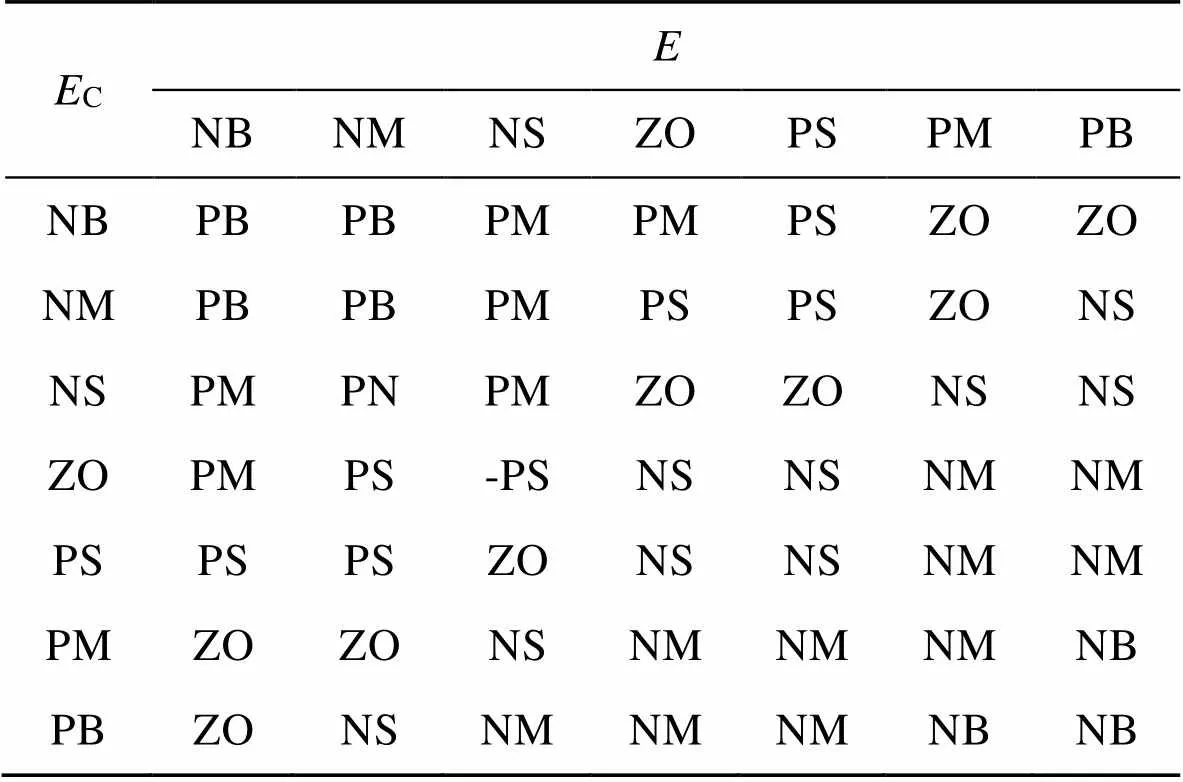
Tab.1 ΔKp fuzzy rule control

系统根据控制规则进行模糊控制。使用MATLAB中的Ruler Editor模块编写模糊规则，使用Mamdani进行模糊推理，得出模糊控制的模糊控制规则，如图8～10所示。

表2 Δi模糊规则控制

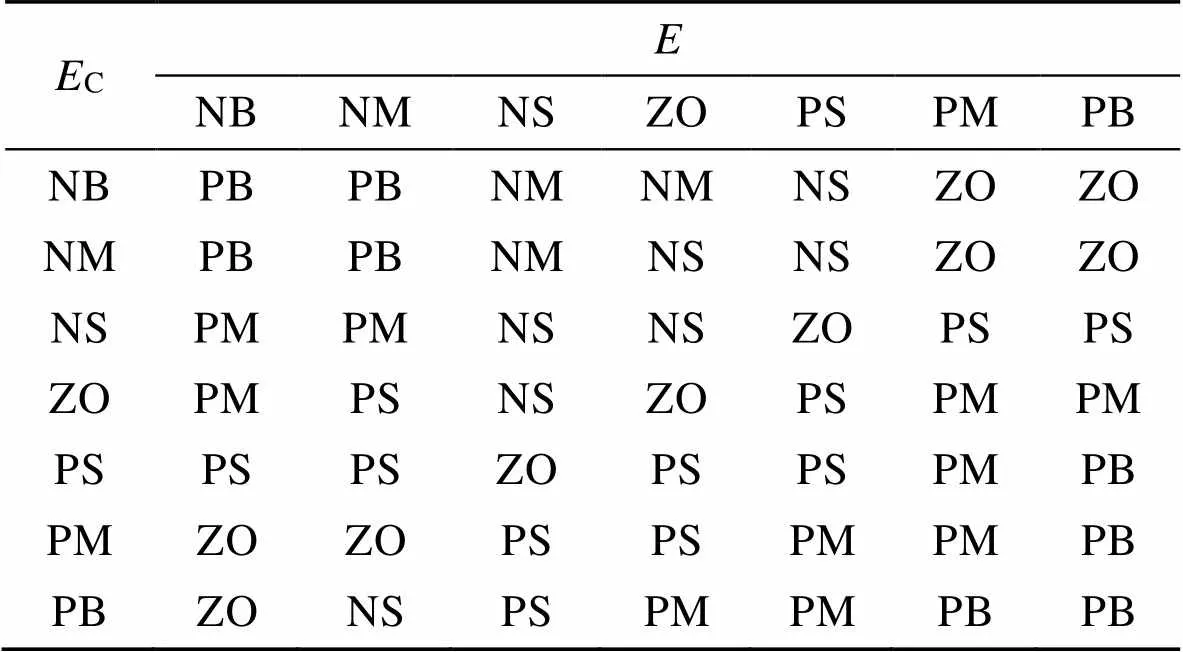
Tab.2 ΔKi fuzzy rule control

表3 Δd模糊规则控制

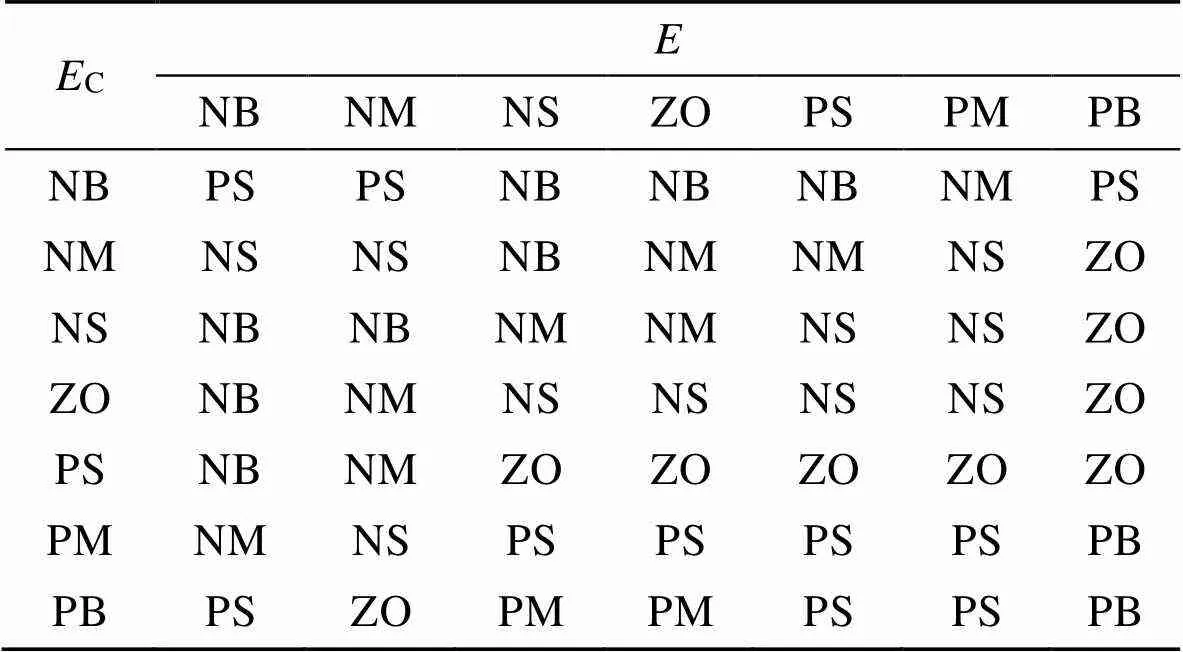
Tab.3 ΔKd fuzzy rule control

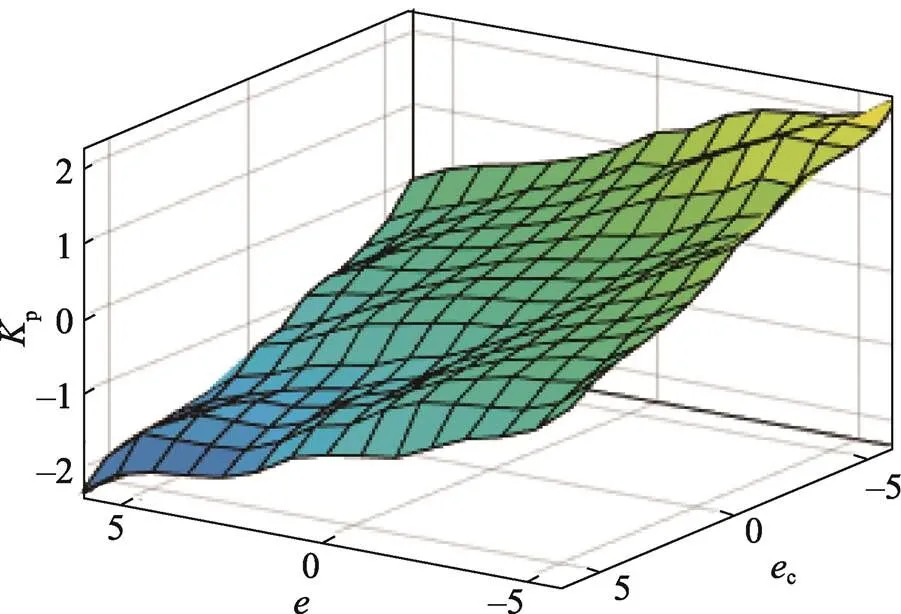
图8 Kp模糊推理的三维空间图

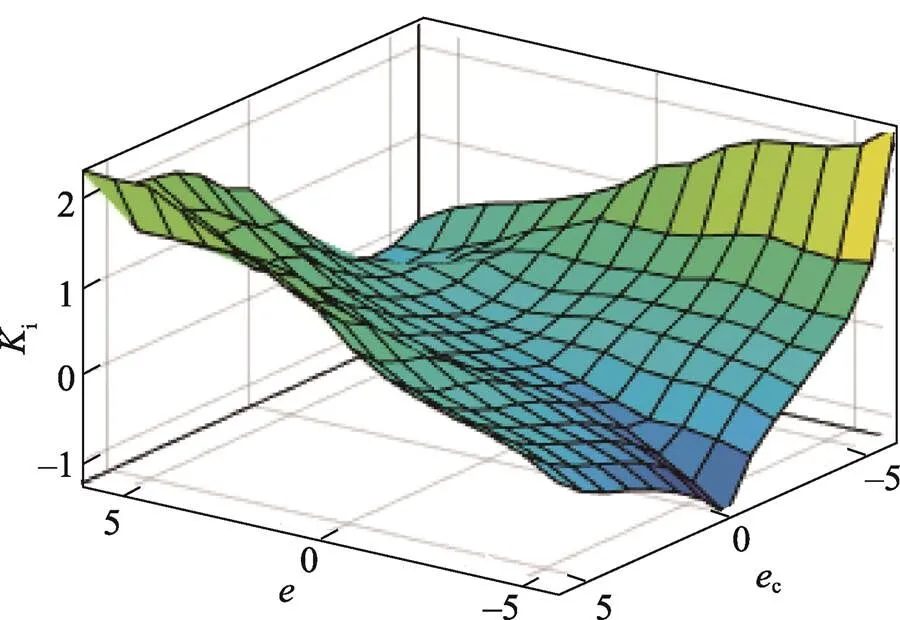
图9 Ki模糊推理的三维空间图

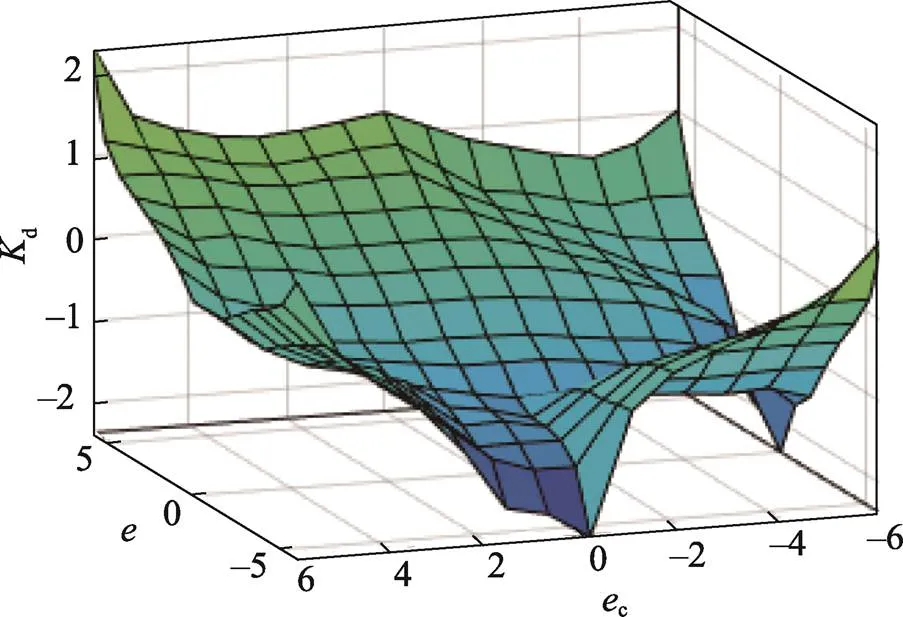
图10 Kd模糊推理的三维空间图

将p、i、d模糊推理的三维空间整理成p、i、d修正参数的表格。如表5～7所示。

表4p修正参数

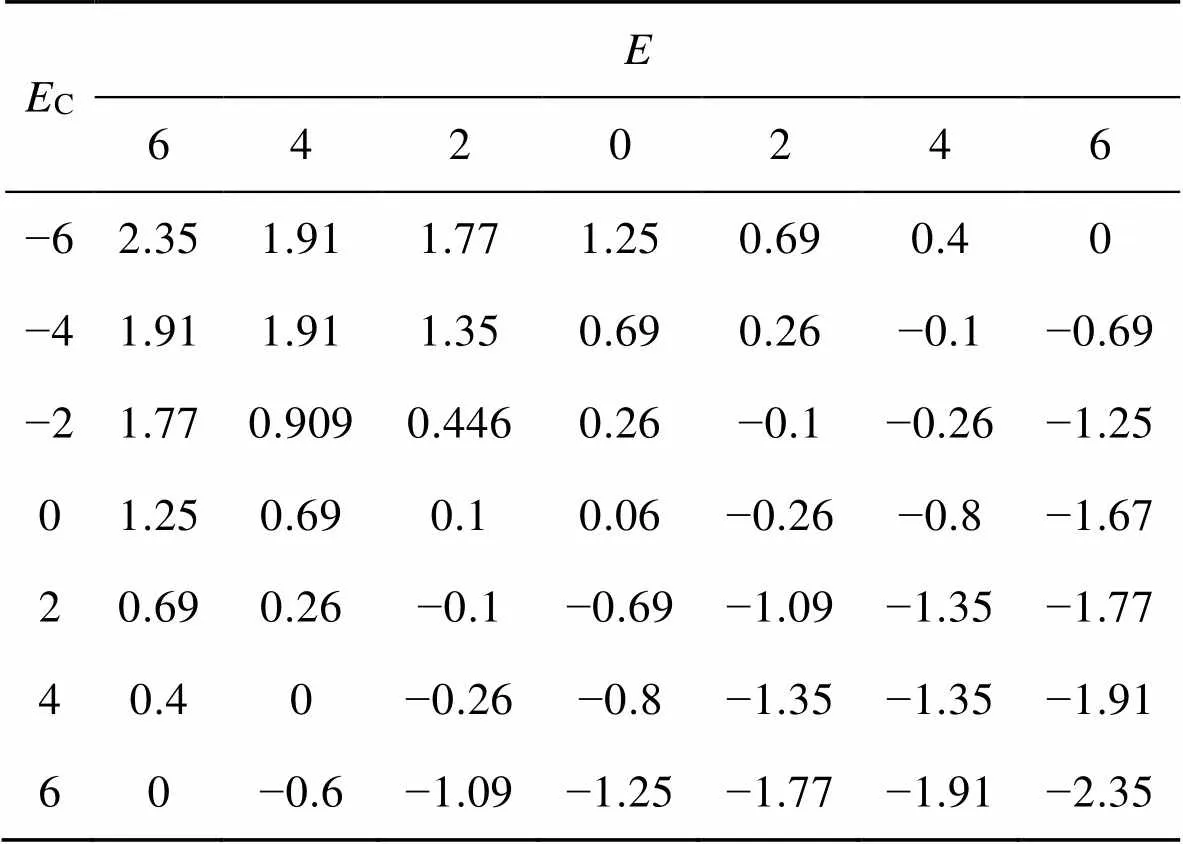
Tab.4 Kp correction parameters

表5i修正参数

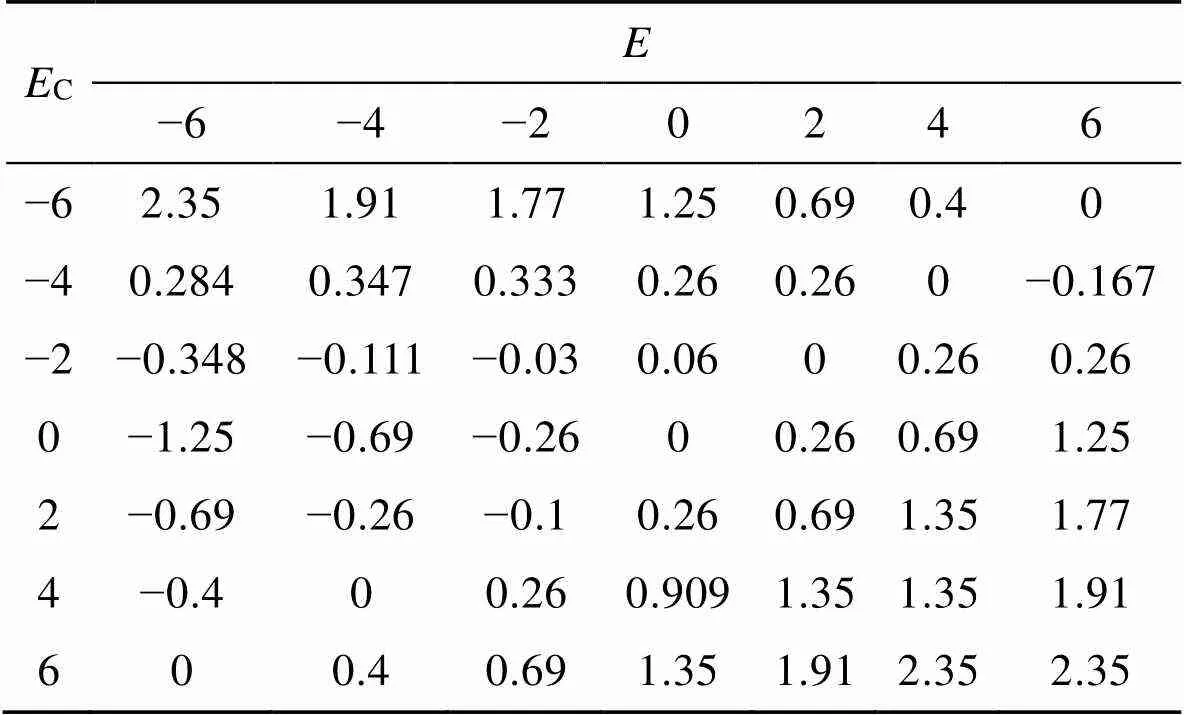
Tab.5 Ki correction parameters

表6d修正参数

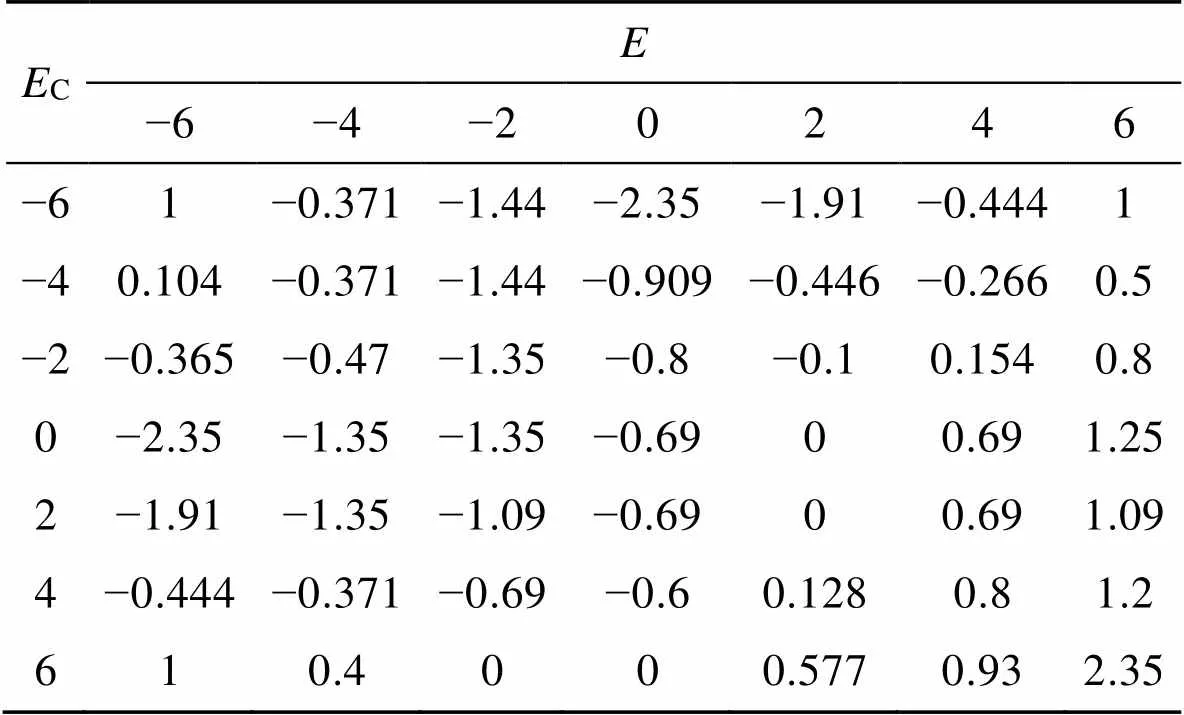
Tab.6 Kd correction parameters

4 仿真分析

在Matlab中进行仿真分析[18]，模糊PID与PID控制结果显示，模糊PID控制在稳定时间、超调量和上升时间都展现出更好的性能。PID控制器与模糊PID控制器Simulink仿真框图如图11所示。

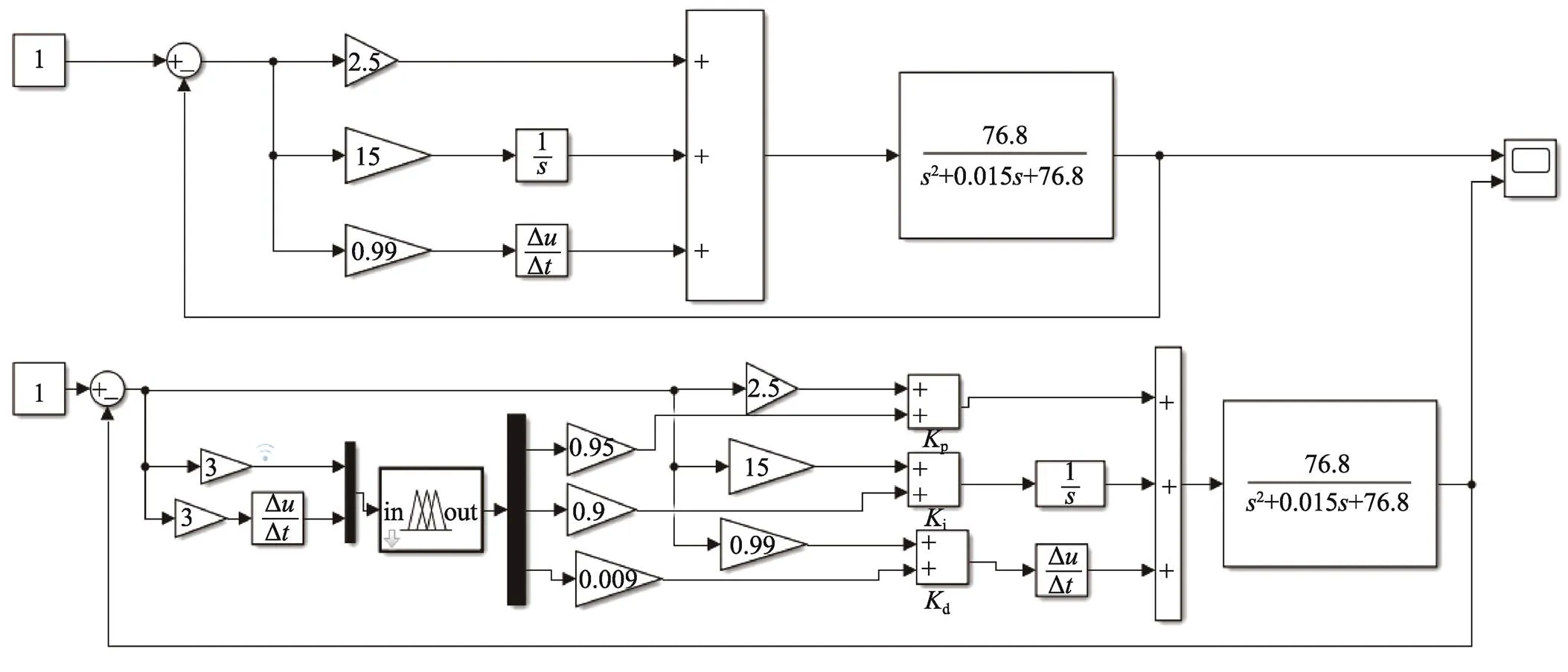
图11 PID控制器与模糊PID控制器Simulink仿真框图

由图12可知，在同样的PID初始参数下，传统PID稳定时间为5 s，上升时间为0.7 s，超调量约为28%；模糊PID稳定时间为1.7 s，上升时间为0.55 s，超调量约为25%。稳定时间减少了66%，快速性提高了21%，超调量减少了10%，仿真效果如图12所示。

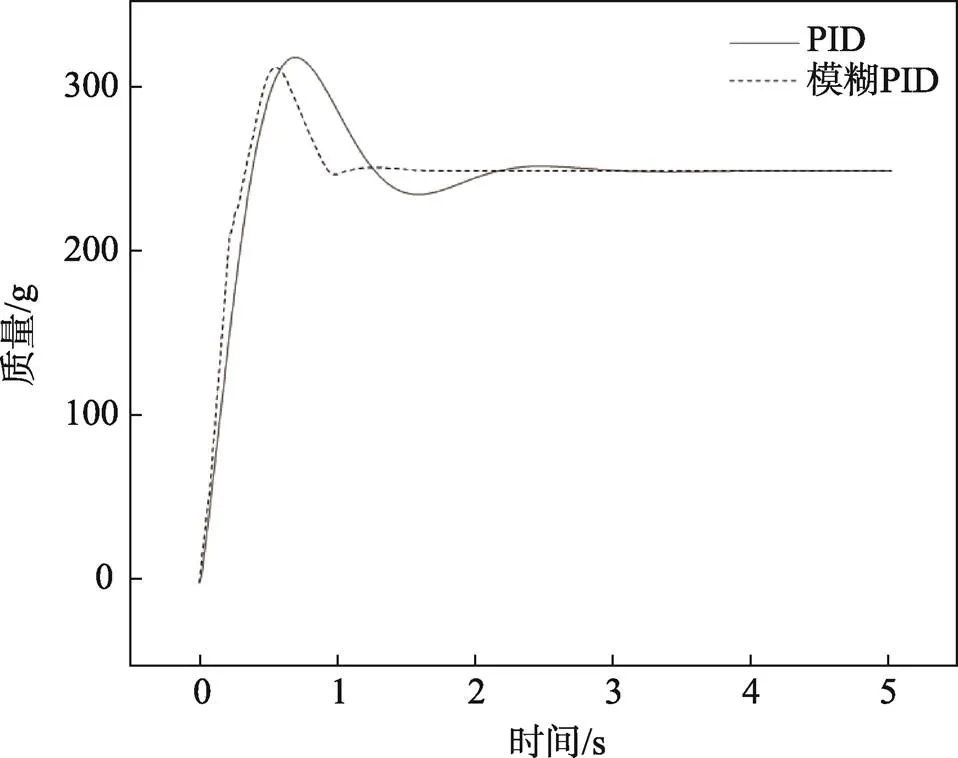
图12 仿真效果对比

5 结语

在针对螺旋加料机构控制系统中，避免系统滞后性的影响，在传统PID控制的基础上增加了模糊控制。与PID控制器比较，该模糊PID控制器具有比PID控制器有更好、更快的稳定性，更高的快速性和更低的超调量。仿真结果显示，与传统PID控制系统对比，模糊PID控制快速性提高了21%，稳定时间减少了66%，超调量减少了10%。

模糊控制算法能实时调节PID的控制参数，PID参数得到实时优化，使螺旋加料机构能快速、准确并稳定的工作，从而提高螺旋加料机构给料的效率和精度。

[1] 戴宏民, 戴佩燕, 周均. 中国包装机械发展的成就及问题[J]. 包装学报, 2012, 4(1): 61-65.

DAI Hong-min, DAI Pei-yan, ZHOU Jun. Achievements and Problems in China's Packaging Machinery Developments[J]. Packaging Journal, 2012, 4(1): 61-65.

[2] 张西良, 路欣, 毛翠云. 粉粒状物料混合式定量充填技术研究[J]. 计量学报, 2003, 24(4): 310-313.

ZHANG Xi-liang, LU Xin, MAO Cui-yun. Study on the Techniques of Composite Type Quantifying-Filling for Powder and Particle Materials[J]. Acta Metrologica Sinica, 2003, 24(4): 310-313.

[3] 王艳, 陈静, 王志山, 等. 基于模糊神经网络PID控制的粉体包装计量控制系统[J]. 食品与机械, 2020, 36(1): 136-139.

WANG Yan, CHEN Jing, WANG Zhi-shan, et al. Powder Packaging Measurement Control System Based on Fuzzy Neural Network PID Control[J]. Food & Machinery, 2020, 36(1): 136-139.

[4] 刘江, 李海龙. 动态定量称量包装系统BP神经网络PID控制算法[J]. 包装工程, 2017, 38(5): 78-81.

LIU Jiang, LI Hai-long. PID Control Algorithm of BP Neural Network of Dynamic Quantitative Weighing Packaging System[J]. Packaging Engineering, 2017, 38(5): 78-81.

[5] 宋欢. 定量螺旋输送机的优化设计及模拟[D]. 青岛: 青岛科技大学, 2016.

SONG Huan. Optimization Design and Simulation of Quantitative Screwconveyor[D]. Qingdao: Qingdao University of Science and Technology, 2016.

[6] 吴宇平, 章家岩, 章磊, 等. 定量称重包装系统RBF神经网络PID控制研究[J]. 安徽工业大学学报(自然科学版), 2014, 31(3): 299-302.

WU Yu-ping, ZHANG Jia-yan, ZHANG Lei, et al. A Study of Quantitative Weighing Packaging System Based on RBF Neural Network PID Control[J]. Journal of Anhui University of Technology (Natural Science), 2014, 31(3): 299-302.

[7] 陈静, 王志山, 徐雪萌, 等. 基于模糊控制的失重秤粉体包装精度研究[J]. 包装工程, 2019, 40(17): 153-158.

CHEN Jing, WANG Zhi-shan, XU Xue-meng, et al. Research on Powder Packaging Accuracy of Weightless Scale Based on Fuzzy Control[J]. Packaging Engineering, 2019, 40(17): 153-158.

[8] 邹剑平, 苏焕欧, 曾庆丰. 定量螺旋输送器分析与改进[J]. 机电信息, 2013(12): 99-100.

ZOU Jian-ping, SU Hua-nou, ZENG Qing-feng. Analysis and Improvement of Quantitative Screw Conveyor[J]. Mechanical and Electrical Information, 2013(12): 99-100.

[9] 徐文强, 闫剑虹. 二相混合式步进电动机传递函数模型推导[J]. 空间电子技术, 2011, 8(3): 50-53.

XU Wen-qiang, YAN Jian-hong. Derivation of Transmission Function Model of Two-Phase Hybrid Stepping Motor[J]. Space Electronic Technology, 2011, 8(3): 50-53.

[10] 周碧书. 步进电动机的传递函数研究法[J]. 微电机, 1989, 22(1): 9-14.

ZHOU Bi-shu. Utilize the Transfer Function for Studying on Stepping Motor[J]. Micromotors, 1989, 22(1): 9-14.

[11] 李浩, 黄潇嵘, 孙海林, 等. 一种新型太阳阵驱动机构用两相步进电机驱动技术研究[J]. 科学技术创新, 2021(7): 190-192.

LI Hao, HUANG Xiao-rong, SUN Hai-lin, et al. Research on Driving Technology of Two-Phase Stepping Motor for a New Type of Solar Array Driving Mechanism[J]. Scientific and Technological InnovationInformation, 2021(7): 190-192.

[12] 杨晓, 董娜, 王国柱. 基于模糊短反馈PID控制的粉末包装计量控制系统[J]. 包装工程, 2019, 40(9): 148-153.

YANG Xiao, Dong Na, WANG Guo-zhu. Powder Packaging Metering Control System Based on Fuzzy Short Feedback PID Control[J]. Packaging Engineering, 2019, 40(9): 148-153.

[13] 王圣斌. 自动化食品包装机械的控制系统优化设计[J]. 机械设计与制造, 2020(11): 297-300.

WANG Sheng-bin. Optimal Design of Control System for Automatic Food Packaging Machinery[J]. Machinery Design & Manufacture, 2020(11): 297-300.

[14] 许高齐, 陈玉, 王鹏. 混合式步进电机模糊PID控制器设计仿真[J]. 安徽工程大学学报, 2019, 34(6): 39-45.

XU Gao-qi, CHEN Yu, WANG Peng. Design Simulation of Hybrid Stepping Motor Fuzzy PID Controller[J]. Journal of Anhui Polytechnic University, 2019, 34(6): 39-45.

[15] 温玉春, 刘祺君. 基于模糊PID的包装机热封切刀温度控制[J]. 包装工程, 2017, 38(3): 109-113.

WEN Yu-chun, LIU Qi-jun. Temperature Control of Heat-Sealing Cutter of Packaging Machines Based on Fuzzy PID[J]. Packaging Engineering, 2017, 38(3): 109-113.

[16] 赵健, 马西庚, 王艳丽, 等. 基于模糊控制的皮带给料式定量包装秤优化控制研究[J]. 电气自动化, 2015, 37(1): 24-26.

ZHAO Jian, MA Xi-geng, WANG Yan-li, et al. A Research on Optimization of Feeding Belt Quantitative Packaging Scale Based on Fuzzy Control[J]. Electrical Automation, 2015, 37(1): 24-26.

[17] 张昱生. 自动定量充填机控制系统研究[D]. 秦皇岛: 燕山大学, 2017.

ZHANG Yu-sheng. Research on Control System of Automatic Quantitative Filling Machine[D]. Qinhuangdao: Yanshan University, 2017.

[18] 宋超, 曹翱, 温家玺. 自适应模糊PID控制器的设计及MATLAB仿真[J]. 现代制造技术与装备, 2018(7): 203-205.

SONG Chao, CAO Ao, WEN Jia-xi. Design of Adaptive Fuzzy PID Controller and MATLAB Simulation[J]. Modern Manufacturing Technology and Equipment, 2018(7): 203-205.

Powder Feeding Accuracy Control of Screw Feeding Mechanism Based on Fuzzy PID

FU Hai-ming, HUANG Xing-yuan*, QIU Guang-jun, CHEN Da

(Jiangxi Province Key Laboratory of Lightweight and High-strength Structural Materials, School of Advanced Manufacturing, Nanchang University, Nanchang 330031, China)

The screw feeding mechanism has problems such as poor sensor response time, system delay, nonlinearity, etc., and the use of volumetric methods to measure the weight of the filling material results in large filling errors. Therefore, the work aims to propose a measurement control system for a screw feeding mechanism based on fuzzy PID control. Fuzzy PID was used to control the screw powder feeding device, and fuzzy rules were adopted to control the proportion, integral, and differential parameters of PID to achieve parameter self-adjustment. The fuzzy PID control system was simulated based on the Simulink module in MATLAB. The stability time of the control system was reduced by 66%, the speed was improved by 21%, and the overshoot was reduced by 10%. The measurement control performance based on fuzzy PID control system is superior to traditional PID.

screw feeding mechanism; measurement control system; fuzzy control; PID control; MATLAB; Simulink

TP273+.4

A

1001-3563(2023)23-0164-07

10.19554/j.cnki.1001-3563.2023.23.020

2023-02-24

责任编辑：曾钰婵