滑模控制下多Euler-Lagrange系统预设时间二分一致性

陶 梦 ,刘小洋,2†,曹进德 ,邵 劭

(1.江苏师范大学计算机科学与技术学院,江苏徐州 221116;2.系统控制与信息处理教育部重点实验室,上海 200240;3.东南大学数学学院,江苏南京 210096;4.东北大学秦皇岛分校控制工程学院,河北秦皇岛 066004)

1 引言

随着计算机技术和通信技术的飞速发展,多智能体系统的协同工作模式引起了人们的极大兴趣.特别是近年来,由于具有操作成本低、鲁棒性强、高容错性、高效率和并行性等优良特性,多智能体系统已经在移动机器人、智能电力网络、传感器网络和智能交通控制等诸多工业领域得到了广泛地应用.考虑到实际系统多为复杂的非线性系统,一般的线性模式不再适用,非线性系统开始受到众多研究者的关注.其中,Euler-Lagrange系统作为一种经典的非线性系统,其可以描述机器人、机械臂、地面车辆和航天器等复杂的动力学系统,已经被广泛应用于工业生产、空间探索、灾难救援等领域[1–2].此外,伴随着网络科学的持续发展,多Euler-Lagrange系统(multiple Euler-Lagrange systems,MELS)在空间对抗和航天器协同攻击等军事领域的应用已经获得了极大地推广.因此,研究MELS的协同控制问题具有重要的理论价值和现实意义.

MELS的一致性是多智能体系统协同控制领域的热点问题.近年来,众多学者对其进行了大量研究并取得了一些研究成果[3–5].例如,文献[3]基于自适应分布式观测器解决了不确定MELS的领导–跟随一致性问题.文献[4]在传统采样策略的基础上提出了一类时变采样策略实现了MELS的一致性.然而,上述成果均是基于网络中各节点之间仅存在合作关系的假设而实现的.事实上,现实生活中的个体之间不仅存在合作关系而且也存在对抗关系.例如,两党制中,当其中一个政党的领导人对某个特殊事件发表观点,同一阵营的成员会表示赞成,而对立阵营的成员则会表示反对[6].这表明同一阵营的成员之间是合作关系,而不同阵营的成员之间是对抗关系.对此,Altafini在文献[7]中引入符号图的概念,将对抗关系表示为节点间的负边,合作关系表示为节点间的正边.如此,在合作–对抗网络中,多智能体系统二分一致性就演变成控制目标的模是相同的,而符号则相反.在此基础上,文献[8]利用异步脉冲控制策略实现了具有领导者的多智能体系统的分布式二分一致性.文献[9]分别研究了在细节平衡图与细节非平衡图条件下多智能体系统的有限时间二分一致性.

另一方面,被控系统往往要求在有限时间内收敛,因此收敛速度是评价控制协议性能的一个重要指标.为了加快多智能体系统的收敛速度,众多优化控制时间的控制方法被提出,如有限时间和固定时间控制策略[10–16].但是,无论是有限时间控制策略还是固定时间控制策略都有一定的保守性,其收敛时间严重依赖系统参数,甚至是系统初值,这使得控制协议无法完成一些对时间要求较高的任务.为了克服以上缺陷,预设时间控制策略开始走入人们视线.多智能体系统的预设时间控制能使系统在任意事先指定的时间内实现一致性,同时确保该时间与其它任何参数无关,完全根据任务需要预先设置.截止目前,多智能体系统预设时间一致性已经取得了一些研究成果[17–19].例如,文献[17]基于分布式观测器和滑模控制策略实现了二阶多智能体系统预设时间一致性.但是,目前关于MELS预设时间二分一致性的研究成果较少.

此外,由于复杂多变的工作环境,多智能体系统不可避免地会受到各种干扰的影响.鉴于滑模控制对外部干扰具有良好的鲁棒性,文献[20]基于滑模控制理论和图论提出了有限时间滑模跟踪控制协议,实现了Euler-Lagrange网络系统领导–跟随有限时间协同追踪.文献[21]基于有限时间滑模观测器,解决了在速度不可测情况下多智能体系统有限时间一致性问题.文献[22]提出了全新的滑模控制器,实现了具有多个领导者的MELS固定时间一致性.但是,现有的文献大多集中在有限时间滑模控制和固定时间滑模控制,对于如何设计新的滑模控制策略来保证MELS的预设时间二分一致性仍然有待解决.

基于上述讨论,本文主要研究了具有外部干扰的MELS的预设时间二分一致性问题.本文主要创新点如下:

1)与文献[3–5,10–12]中的完全一致性不同,本文在结构平衡图下,实现了MELS的预设时间二分一致性,最终的一致性目标的模相同,但是符号相反;

2)与文献[22]考虑的无干扰的系统相比,本文研究了具有外部扰动的MELS,采用预设时间控制方法克服了外部干扰对系统实现二分一致性的影响;

3)与文献[22]中的控制时间依赖于系统参数不同,本文借助时变函数方法设计了全新的预设时间滑模控制协议,保证MELS在预设时间内实现二分一致性,且控制时间可以根据任务需要而预先设定.

2 问题描述

2.1 代数图论

考虑由有向符号图G(V,E,A)来描述N个跟随者之间的通信拓扑,其中:V={v1,v2,···,vN}表示顶点集;E ⊆V×V表示有向边集;(vj,vi)∈E表示智能体i可以接收到智能体j的信息,但反之不成立;A=[aij]∈RN×N表示图G的邻接矩阵,如果(vj,vi)∈E,那么aij0,否则aij=0.本文不考虑闭环,即aii=0.点vi1到点vij的路径可以由有序点集{vi1,vi2,···,vij}来表示,其中(vik,vik+1)∈E,k=1,2,···,j-1.如果有向图中任意两点之间都有一条路径连接,那么称图G为强连通图.

图G的拉普拉斯矩阵L=[lij]∈RN×N定义如下:

对于符号图G,如果顶点集V可以划分为两个集合V1和V2,满足V1∪V2=V,V1∩V2=∅,∀vi,vj ∈Vm,m∈{1,2},aij≥0并 且∀vi ∈Vm,vj ∈V3-m,m∈{1,2},aij≤0,那么称图G为结构平衡图,否则称图G为结构非平衡图.

将领导者节点记为v0,假设领导者只发送信息,不接收跟随者的信息.如果第i个跟随者可以直接获取领导者的信息,则bi>0,否则bi=0.记对角阵B=diag{b1,b2,···,bN},并定义新矩阵H=L+B.

2.2 多Euler-Lagrange系统

考虑由N个跟随者组成的多Euler-Lagrange系统,第i个Euler-Lagrange系统定义如下:

其中:qi,,∈Rp分别代表广义坐标、速度和加速度向量;Mi(qi)∈Rp×p表示正定对称惯性矩阵;Ci(qi,)∈Rp×p表示科里奥利–向心力矩阵;gi(qi)∈Rp表示重力;τi∈Rp表示作用在系统上的控制器;δi∈Rp为有界的外部干扰,满足‖Mi(qi)δi‖≤σ,σ为正常数.

定义动态领导者如下:

其中q0,,∈Rp分别表示领导者的位置、速度和加速度信息.

式(1)可以进一步写成矩阵形式为

2.3 相关假设与引理

假设1领导者的加速度有界,满足‖(t)‖≤ε,ε为正常数.

假设2有向符号图G是强连通的并且结构平衡,且至少有一个节点可以直接接收领导者的信息.

引理1[7]若图G是结构平衡的,则存在对角阵D=diag{d1,d2,···,dN},di ∈{-1,1},i=1,2,···,N,使得矩阵DAD的所有元素非负.

对于MELS(1),预设时间二分一致性定义如下:

定义1若以下

成立,则称MELS(1)实现了预设时间二分一致性,其中Tf是系统实现一致性的时间,该时间可以根据任务需求预先设计.

注1二分一致性是指多智能体系统中的各智能体通过彼此的合作及对抗交互,达到两组模值相同但符号相反的状态.它可以用来刻画同时具有竞争与合作关系的多智能体系统的演化规律.此时系统可以分为具有相反任务目标的两组阵营并进行动力学分析,常应用于多移动机器人对抗系统、社交网络的观点分析等领域.

3 主要结论

本节提出一种新的滑模控制策略来实现带有动态领导者的MELS预设时间二分一致性.

首先定义追踪误差

其中: 常数ϱ>1,t0>0是系统初始时刻,tf>0是系统收敛所花费的时间,Tf=t0+tf是预先设计的收敛时间.

基于函数ϕ(t),设计终端滑模s(t)如下:

再引入函数φ(t),即

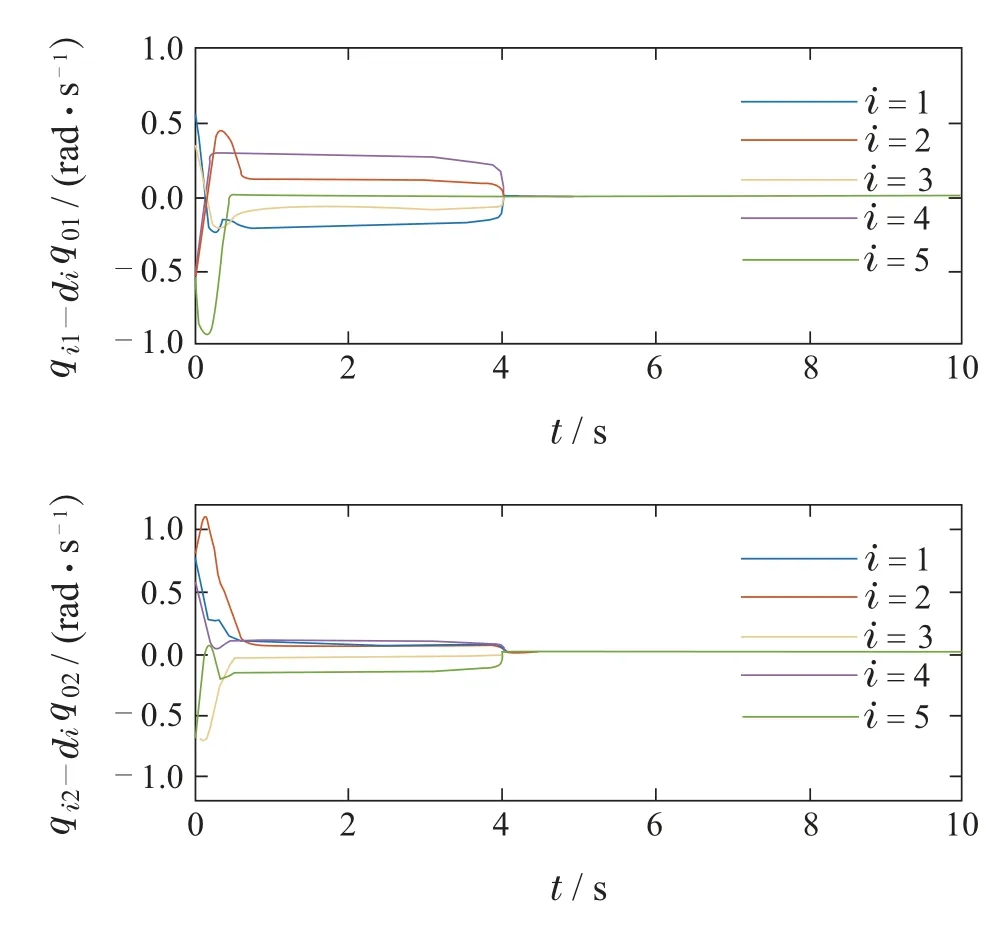
其中: 常数ϱ1,ϱ2>1;T1表示滑动时间,满足0

基于时变函数ϕ(t)与φ(t),设计控制器如下:

其中参数k>0.

定理1在假设1、假设2和控制协议(12)下,如果控制参数满足k≥,则MELS(1)在t=Tf时实现预设时间二分一致性,并且ui(t)在[t0,∞)上保持有界.

证本文的证明分为3个步骤.首先,证明系统(1)可以在t=t0+T1时到达滑模面s(t)=0;其次,证明系统(1)能在t=Tf时实现二分一致性;最后,证明ui(t)在整个时间区间[t0,∞)上的有界性.

步骤1证明在控制协议(12)下,系统(1)可以在t=t0+T1时到达滑模面s(t)=0.

沿着系统(8)对滑模变量(10)求导得

1)当t∈[t0,t0+T1)时,根据函数φ(t)的定义,式(18)可以写为

基于以上分析可知,MELS(1)在t=t0+T1时到达滑模面s(t)=0,并在[t0+T1,t0+tf)内沿着滑模面滑动.

步骤2证明e1(t)和e2(t)在t=t0+tf时沿着滑模面(10)收敛到原点,即系统(1)在t=Tf时实现二分一致性.

与式(19)–(22)过程相似,可以进一步得到

2)当t∈[t0+tf,∞)时,因为e1(t)在t=t0+tf时刻是连续的,所以有

接下来要证明当t>Tf时,e1(t)≡0,e2(t)≡0.为此,构造以下Lyapunov函数:

基于以上分析可知,当t∈[Tf,∞)时,q-q0≡0,-≡>0.因此,MELS(1)在预设时间Tf时实现了二分一致性.

步骤3证明当t∈[t0,∞),ui(t)恒有界.

由式(9)–(10)(13)可知

与步骤1证明相似,有

然后,将式(34)代入式(31)得

3)当t∈[t0+tf,∞)时,s(t)≡0.由式(31)可知‖u(t)‖在[t0+tf,∞)上恒有界.

综上所述,u(t)在整个时间区间[t0,∞)上恒有界.

证毕.

注2由定理1可知,系统(1)实现二分一致性的时间为Tf,与系统到达滑模面的时间t0+T1无关.无论系统到达滑模面的时间如何设置,只要满足t0+T1

注3控制器ui(t)在t=t0+T1时刻和t=t0+tf时刻的有界性分析相当重要.当时间趋近于t0+T1时,1/φ(t)趋近于无穷;当时间趋近于t0+tf时,1/ϕ(t)和1/φ(t)均趋近于无穷.但是,从式(32)与式(35)可以看出,只要ρ1,ρ2均大于1,就可以确保ui(t)在整个时间区间上的有界性.

注4文献[23]研究了具有动态领导者的MELS预设时间二分一致性问题,但是其要求领导者的动力学方程是线性函数.而本文则没有这种限制,领导者动力学方程可以是非线性的,而且本文进一步考虑了外部干扰对系统的影响.另一方面,文献[23]采用的方法只可以设置实现收敛的时间上界,无法获得精确的收敛时间.然而,本文采用的时变函数控制策略能够精确设置MELS一致性时间,使系统在该时刻实现二分一致性,这在本文的仿真中也已得到验证.此外,文献[23]考虑的拓扑是无向符号图,本文在有向符号图下获得了MELS预设时间二分一致性.

4 数值仿真

本节将给出一个二自由度机械臂系统的数值仿真例子来验证定理1的正确性.这里考虑由5个机械臂系统组成的MELS,第i,i=1,2,···,5个节点的动力学方程如下:

其中g=9.8,记Θi=[ρi1ρi2ρi3ρi4ρi5]T,有Θ1=[0.6 1.1 0.1 0.6 0.3]T,Θ2=[0.8 1.2 0.1 0.9 0.5]T,Θ3=[0.9 1.3 0.2 1.3 0.6]T,Θ4=[1.1 1.4 0.3 1.7 0.7]T,Θ5=[1.0 1.2 0.4 1.6 0.6]T.

图1表示5个跟随者的有向拓扑图G,其中集合V={1,2,3,4,5}可以划分为两个子集V1={1,2},V2={3,4,5}.显然,有向图G是结构平衡的.根据引理1,可以求得D=diag{1,1,-1,-1,-1}.将领导者与跟随者之间的信息交互矩阵设置为B=diag{0.6,0,0.6,0.6,0},则网络拓扑满足假设2.然后,将领导者的动力学方程设置为q0(t)=[-0.1cost-0.1cost]T.领导者与跟随者的初始状态从[-2,2]×[-2,2]中随机选取.

图1 5个跟随者之间的网络拓扑Fig.1 Network topology of five followers

对于控制器(12),分别取t0=0,k=1.8,ρ=1.11,ρ1=1.12,ρ2=1.13,设置系统(36)到达滑模面的时间为t0+T1=2,系统实现二分一致性的时间为Tf=4.不难验证它们的取值满足定理1的条件,由定理1 可知MELS(36)将在t=4 时实现二分一致性.图2–3分别给出了5个跟随者的位置qi与速度,领导者的位置q0与速度(由虚线表示)随时间演化的过程,而图4–5则分别给出了二分追踪误差qi-diq0和-di随时间演化的过程.

图2 MELS(36)中qi的演化过程Fig.2 Evolution of qi in MELS(36)

由图2和图3可以看出,MELS(36)在t=4时实现了二分一致性.子集V1中的2个节点的位置和速度状态在t=4时与领导者趋近一致,而子集V2中的3个节点的位置和速度在t=4时与领导者的位置和速度的模相同,但是符号相反,验证了定理1的结论.

图3 MELS(36)中的演化过程Fig.2 Evolution of in MELS(36)

由图4和图5可以看出,5个跟随者的二分追踪误差在预设时间t=4时收敛到零,与理论分析的实现二分一致性的时间相同.然而文献[23]的预设时间控制算法仅能预设实现二分一致性收敛时间的上界,这与本文的算法有着本质的不同.因此,本文提出的预设时间二分一致性算法可以应用于对驻留时间要求精确的复杂任务.

图4 二分追踪误差qi-diq0的演化过程Fig.4 Evolution of bipartite tracking errors qi-diq0

图5 二分追踪误差-di 的演化过程Fig.5 Evolution of bipartite tracking errors -di

5 结论

本文提出了一种基于终端滑模方法的MELS预设时间二分一致性控制算法.针对结构平衡图下具有动态领导者的MELS,设计预设时间终端滑模和分布式预设时间控制器保证系统实现预设时间二分一致性目标.最后,通过仿真实验验证了本文理论结果的有效性.在未来的工作中,笔者将进一步研究在有向图拓扑结构下,切换系统的预设时间二分一致性问题.