可重入柔性流水车间有限缓冲区容量动态预留方法

韩忠华 ,刘约翰†,史海波

(1.中国科学院网络化控制系统重点实验室,辽宁沈阳 110016;2.中国科学院沈阳自动化研究所,辽宁沈阳 110016;3.中国科学院机器人与智能制造创新研究院,辽宁沈阳 110169;4.中国科学院大学,北京 100049;5.沈阳建筑大学信息与控制工程学院,辽宁沈阳 110168)

1 引言

在客车制造和半导体生产等关键制造行业中,其多芯片半导体封装线的键合工序段和客车生产线的多遍彩条工序段,存在一种具有可重入工序的有限缓冲区柔性流水车间排产(reentrant flexible flow-shop with limited buffer scheduling,RFFLBS)问题.由于可重入工序的存在,会使工件的加工路径更加复杂,又由于有限缓冲区的存在,更增加了局部任务指派和资源调度的难度.在生产过程中,执行可重入工序的工件会再次折返进入该重入工序所对应的缓冲区,若该缓冲区为有限缓冲区,则来自前道工序完工的工件与折返重入的工件将争夺缓冲区资源,如果该缓冲区中存储的工件数量达到其容量上限,前道工序的工件无法进入该缓冲区,导致前道工序发生阻塞,同时,本应折返重入该缓冲区的工件,也由于缓冲区无空闲缓冲车位而被滞留在其当前的完工工位上,导致后道工序也发生了生产阻塞,前、后道工序同时发生阻塞时会产生一种很难自解的生产阻塞现象即死锁现象,严重的情况下会使得整个生产进程停滞.由于会出现死锁现象,这进一步增大了排产的不确定性,提高了生产排产难度,较一般柔性流水车间排产问题更为复杂.

为研究RFFLBS,可分别从可重入工序和有限缓冲区两类问题展开,提取两类问题的特点和特征,分析求解方法和研究进展,为更好解决RFFLBS问题做好准备.客车等大体积在制品的生产车间由于受到物理空间的限制,无法设置大容量的缓冲区,即缓冲区容量受限,同时企业对于挖掘现有生产资源潜力、提升生产资源利用率越来越重视,因此,近年来具有有限缓冲区的排产问题引起了越来越多的关注.Zhang等[1]设计了一种结合差分进化的混合方法与一种灵活的缓冲区服务策略的方法求解具有有限缓冲区的柔性流水车间调度问题;Zhao等[2]采用一种改进的粒子群算法,该算法通过在标准粒子群公式添加线性递减扰动项,集中资源求解可行解;Tao等[3]提出一种启发式算法,并在适当时间使用,以减少具有有限缓冲区的柔性流水车间的阻塞现象,来获得高质量的排产结果;Xie等[4]提出了一种基于变邻域搜索策略的Memetic算法,并验证了所提算法的有效性;Pan等[5]采用了一种改进的混沌和声算法,该算法在局部搜索中引入概率跳跃,对解决具有有限缓冲区的柔性流水车间排产问题具有很好的效果.同时,在客车制造、半导体封装等行业中还广泛存在一类具有可重入工序的柔性流水车间,依据加工流程被加工工件需多次进入可重入工序段加工.随着产品种类的增多和产品批量的增大,工件的迁移和加工过程中相互之间的影响和制约进一步加剧,使得排产过程中的不确定性增加.因此,具有可重入工序的柔性流水车间排产问题也成为近些年学者研究的热点问题.Hekmatfar等[6]提出了以最小最大完工时间为目标的一种偏随机密钥混合遗传算法,用于求解两阶段的具有可重入工序排产问题;Xie等[7]针对车间具有可重入工序段车间排产问题,提出了两种可能解决问题的情况并等效成两阶段混合流水车间问题进行求解;Zhou和Zhong[8]采用一种基于松弛机器能力约束的拉格朗日松弛算法,求解可重入混合流水车间排产问题;Topaloglu和Kilincli[9]提出了一种改进的瓶颈转换启发式算法,将问题分解成多个单机问题进行求解;Chen等[10]针对具有可重入工序排产问题,提出一种快速粒子群优化算法来提高求解大规模数据效率.当前,大部分学者对具有有限缓冲区和具有可重入工序的排产问题分别进行单独研究,并都从全局优化算法角度求解这些问题,少有学者对两类问题并存的生产车间排产问题进行研究.

死锁现象是一种由于严重生产阻塞而导致的生产停滞现象,如果不对死锁现象进行控制,会给生产企业的日常生产带来巨大影响,严重制约生产进程,增加了生产管控的难度.邢科义等[11]通过将死锁避免策略嵌入到粒子群算法中,提出一种无死锁改进粒子群调度算法,去除解中可能导致死锁现象出现的加工序列,避免死锁现象出现;Xing等[12]建立了一种无死锁遗传调度算法,设计一种具有多项式复杂性的死锁避免策略(deadlock avoidance policy,DAP),采用DAP对遗传算法中的染色体的可行性进行检测与修复,来获得可行解;Fan等[13]提出了一种改进遗传算法,通过判断转换触发条件来检验和修正算法中染色体即生产序列的可行性,使每个染色体都能被解码成一个可行的调度序列,避免死锁现象的出现.当前学者对于死锁问题,更多是从全局优化的角度开展研究,多数采用改进的群体进化算法,通过增加算法的相应规则,去除可能产生死锁的解,来解决死锁问题,但是这类方法会随着需求产能增加,可行解将迅速减少,当需求产能与提供产能达到一定比例时将无法得到可行解,通过在所有解中筛选可行解的方法也极大增加了运算的时间成本,因此当前死锁问题的这类解决方法不适合在实际工程项目中应用.

通过对近年来相关研究文献的分析,目前少有学者开展对RFFLBS问题进行系统的研究,也少有学者对RFFLBS中出现的死锁现象进行更深入的探索,也没有从控制工件在缓冲区分配过程中降低死锁现象出现的概率的角度,来探索解决RFFLBS中出现死锁现象的方法.

若能利用历史生产数据对未来可能出现的死锁现象进行预测,干预生产任务在各工序的移动,保证缓冲区资源的合理分配,避免死锁现象的发生,则无需为车间配置冗余的缓冲区资源和对已配置在车间中的缓冲区资源进行大规模的调整,对于节约生产资源、降低企业的整体生产成本具有重要意义.

为解决死锁现象,本文提出一种基于马尔可夫链的有限缓冲区动态容量预留方法(dynamic buffer reservation method based on Markov chain,DBRMMC).该方法根据历史生产数据,通过运用马尔可夫链预测,计算并预测缓冲资源释放的概率.根据预测结果对局部调度过程进行干预,将折返执行可重入工序的工件预留缓冲区容量,减少工件对缓冲区资源的争夺,降低死锁现象出现的概率.研究内容与以往研究工作不同之处在于: 1)深入分析RFFLBS过程中死锁现象,找到死锁现象产生的原因;2)通过调度缓冲区资源来干预局部指派过程,避免对生产线已配置资源进行大规模重新调整和扩充的前提下,就可以有效的克服死锁现象,并获得较好的排产结果;3)提出DBRMMC方法,通过预测生产过程中出现死锁现象时生产线的生产运作状态,提前为执行重入工序的工件预留缓冲区容量,并对该方法进行改进,引入基于自适应阈值二值化算法的偏差补偿措施,结合基于高响应比优先算法(highest response ratio next,HRRN)的局部指派方法,提出一种改进的基于马尔可夫链的有限缓冲区容量动态预留方法(improved DBRMMC with local dispatching rule based on HRRN,IDBRMMC-HRRN).

2 问题描述

2.1 问题描述

LBRFFS问题可描述如下: 存在n个工件的待加工队列{J1,J2,···,Jn},需经过m道工序的加工,其中,nrm道为非可重入工序,在非可重入工序段内;rm道为可重入工序,在可重入工序段内,每道工序都由一组数量不完全相同但相同型号的并行机(工位)组成.每个并行机代表一个工位,每个工位同一时刻只能加工一个工件.受生产资源约束的影响,缓冲区只能容纳有限数量的工件.工件依据对应工艺流程顺序经过指定的工序进行加工,工件在重入工序中至少加工一次,每个工件有不同的重入次数rtsi(工件Ji总共被加工nrm+rm×rtsi次).工件每经过一道工序,需选择一个工位进行加工,完工后移出至对应的缓冲区存放.当后道序工位空闲时依据局部指派方法选择工件进行加工.所有工件至少执行一次可重入工序段中全部可重入工序.需执行可重入工序的工件,在遍历可重入工艺段后,需重新进入指定工序对应的缓冲区中等待加工.排产结果要确定工件的工位分配、加工顺序以及工件依据工艺流程在每个工序的开工时间、完工时间.RFFLBS模型示意图如图1所示.

2.2 数学模型

2.2.1 模型参数

n: 工件总数;

Ji: 第i个工件,i ∈{1,···,n};

t: 生产加工过程中某时刻;

rm: 可重入工序数;

nrm: 非可重入工序数;

m: 总工序数,m=nrm+rm;

Oj: 第j道工序j ∈{1,···,m};

Mj:Oj中包含的工位数,j ∈{1,···,m};

Wj,k:Oj中第k个工位,j ∈{1,···,m},k ∈{1,···,Mj};

Bj:Oj对应的缓冲区,j ∈{2,···,m};

Bcj:Bj的最大缓冲容量,j ∈{2,···,m};

bj,p:Bj的第p个缓冲车位,j ∈{2,···,m},p ∈{1,2,···,Bcj};

FLi:Ji的工艺流程,即Ji需经遍历工序的集合,i ∈{1,···,n};

rtsi:Ji遍历可重入工序段次数,i ∈{1,···,n};

fmi:FLi中Ji经过的工序总数,fmi≥m;

li:Ji执行的工序在FLi中顺序号,li ∈{1,···,fmi};

2.2.2 假设变量

2.2.3 约束条件

在前文设置的模型参数和假设变量下建立数学公式,通过数学公式描述在生产过程中各变量间的约束关系,从而反映RFFLBS问题的过程及特点.其中,约束1–5为柔性流水车间约束,影响工件在生产线中如何迁移;约束6–9为有限缓冲区约束,影响工件进出缓冲区和工位;约束10–12为其他约束,保证生产过程具有合理性.

1)约束1.

工件在后道工序开始加工时间大于等于前道工序结束加工时间;

3)约束3.

每经历道工序工件只能选择一个工位进行加工;

4)约束4.

工件需依据工艺流程遍历全部包含的工序;

5)约束5.

工件经过工序总数等于经过的非可重入工序与可重入工序次数之和;

6)约束6.

工序Oj的等待加工队列包含t时刻在对应缓冲区Bj中所有的工件;

7)约束7.

在任意时刻t,待加工队列WAj(t)中的工件数小于等于缓冲区Bj的最大缓冲区容量Bcj;

8)约束8.

在忽略转运时间的前提下,Ji从前道工序移出的时刻等于其进入缓冲区的时刻,且该时刻大于等于在前道工序的完工时间;

9)约束9.

式(9)中,当工件Ji从缓冲区的加工列队中进入加工工序Oj时便立即开始加工;

10)约束10.

不可中断约束: 如果工件在工位上已开始加工,则不能中断,直到完成在该工位的生产过程;

11)约束11.

工位唯一性约束: 一个工位在同一时刻只能加工一道工序;

12)约束12.

工位可用性约束: 所有工位在调度时刻都是空闲可用的.

2.3 阻塞与自解阻塞现象分析

由于在具有有限缓冲区的柔性流水车间的生产线上,只能设置容量有限的缓冲区,当工件完成在前道工序的加工任务时,该工件可能会因无空闲缓冲车位而滞留在前道工序的工位上,影响生产线的局部生产过程,造成阻塞现象.若随着生产过程的继续,后道工序中有工件完工并从工位移出,缓冲区中待加工工件能够进入后道工序执行加工任务,此时缓冲区资源得到释放,被阻塞的工件可从前道工序移入缓冲区,即自解阻塞.如果无法自解阻塞则会导致死锁现象.通过分析生产阻塞现象的形成,进一步讨论自解阻塞的条件,进而分析和得出死锁现象的产生的原因和条件.

例如可重入工序段中包含2个工序且均为3个工位,缓冲区容量为2举例,如图2所示,在可重入工序段存在阻塞,当系统运行至时刻t,Ord中存在完成可重入工序段加工的工件,依据其工艺流程离开可重入工序段,因此Ord中出现空闲Wrd,2,依据局部指派方法,Brd中的工件竞争Wrd,2,Brd出现空余,Oru中完工工件可以进入Brd,即自解阻塞现象.

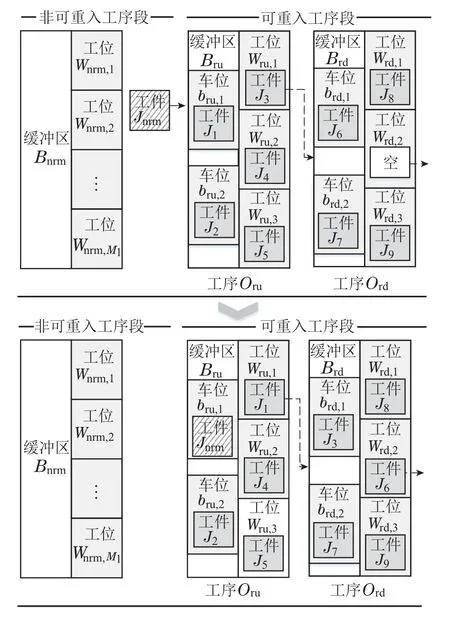
图2 自解阻塞现象示意图Fig.2 Diagram of self-unblocking phenomenon

RFFLBS中生产阻塞现象的数学模型为

其中:WSS(t)j,k表示t时刻可重入工序中工位的加工状态,当工位处于被占用状态时,值取为1;并行工位数Mj在可重入生产工序取值为Mj ∈{Mrd,Mru};b表示t时刻,可重入生产工序的缓冲区中的工件数;Bcj表示可重入生产工序缓冲区的最大容量.

式(10)在t时刻,可重入工序中的工位都处于被占用状态;式(11)在t时刻,缓冲区中存放的工件数达到最大容量;式(12)在t时刻,存在已完工的工件Ji,其将进入可重入工序Oru进行生产.

RFFLBS过程中自解阻塞现象的数学模型为

式(13)表示在Ord中存在不需要进入可重入工序段的工件;式(14)表示在t时刻Ord中存在空闲工位.

2.4 死锁现象分析

假设场景,在t时刻,假设工序Oru,Ord中所有工位都处在加工状态,且缓冲区Bru,Brd均被占满,若顺序发生事件1–6则会出现死锁现象,如图3所示.

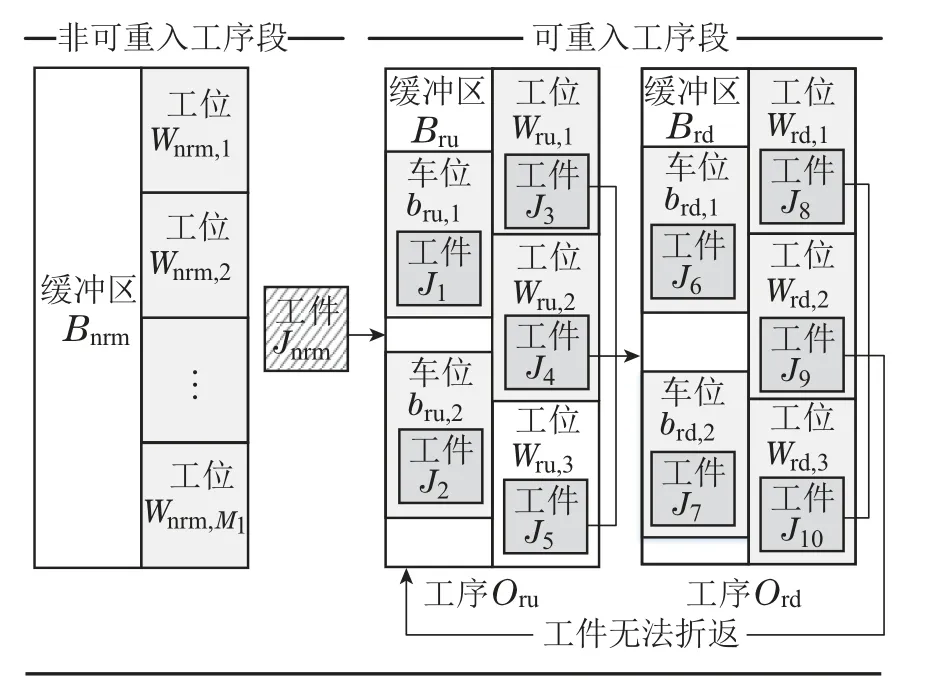
图3 死锁现象示意图Fig.3 Diagram of deadlock

事件1依据其工艺流程J8完成了在Ord中的加工,将进入Bru中的缓冲车位等待加工;

事件2在事件1发生的时候,工件J8不能进入缓冲区Bru,导致J8停留在当前工位Wrd,1上发生阻塞,Brd中的工件无法进入Wrd,1中加工;

事件3在事件1和2发生后,J9完成当前工序的加工,根据J9的工艺流程,将再次进入可重入工序段的工序Oru;

事件4J9所在的工位Wrd,2发生阻塞;

事件5在事件3和事件4发生后J10完成当前工序的加工,根据J10的工艺流程,也将再次进入可重入工序段的工序Oru进行加工;

事件6J10所在的工位Wrd,3发生阻塞.

由于发生连续的阻塞,且在可重入工序段中的工位和对应的缓冲区均不会因生产进程的继续而释放资源,导致工件在生产线中无法移动,致使生产停滞,最终导致死锁现象发生.

数学模型描述和分析t时刻死锁现象如下:

其中: 式(15)表示在t时刻可重入工序段中所有工序Oj,j=ru,rd的全部工位均被占用;式(16)表示在t时刻可重入工序段中所有缓冲区Bj,j=ru,rd的缓冲车位均被占用;式(17)表示存在等待折返可重入工序段前道工序的待加工工件;式(18)表示在非可重入工序段中存在等待进入可重入工序段的待加工工件.

一种特殊情况: 依据工艺流程,可重入工序段中,当最后一道工序工位上的全部工件都需要折返前道工序进行加工时,即Ord中的全部工件均满足条件式(18),则会导致全部工件滞留在当前位置,造成阻塞,如果不采取措施且持续出现阻塞现象,就会导致死锁现象发生,陷入停滞状态.

在上述场景发生之前,如图4,工序Oru的缓冲区Bru还剩下一些缓冲区容量,如果这些缓冲区容量再被来自非可重入工序段的工件占用,Bru被完全占满,接下来事件1–2再发生,则会产生死锁现象.因此探索解决死锁现象的方法重点在,如何干预可重入工序段中第1个工序对应缓冲区资源的使用.

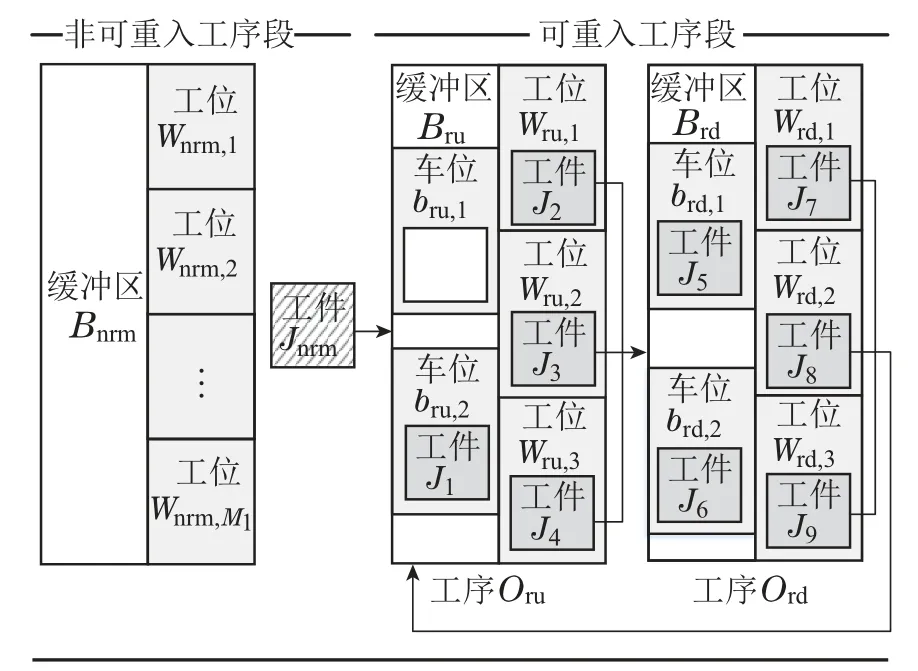
图4 来自非可重入工序段工件争夺缓冲车位Fig.4 The job from non-reentrant process compete for buffer parking spaces

因此,如果能找到预测死锁现象的方法,并采取有效的处理措施,避免死锁现象发生,从而避免了生产资源的浪费,节约了企业的整体生产成本.

3 求解RFFLBS排产问题的方法

针对可重入工序段中首道工序,即工件折返执行的可重入工序,其工位的状态的变化过程是一种随机变化过程符合马尔可夫过程的特性,与近期状态有关而与过去状态无关,具有无后效性.故提出DBRMMC,解决在RFFLBS过程中出现死锁现象问题,并对DBRMMC方法进行进一步的改进,引入基于自适应阈值二值化算法的偏差补偿措施,结合HRRN的局部指派方法,提出IDBRMMC-HRRN.

3.1 DBRMMC方法描述

为了能够为折返执行可重入工序的工件动态预留缓冲区容量,DBRMMC方法通过预测可重入工序段中首道工序中工位加工工件的变化情况,进而预测对应缓冲区缓冲车位的释放概率,根据计算结果判断是否预留缓冲区资源,通过提前预留缓冲区资源,保证折返工件能够顺利进入缓冲区.该方法减少了因来自不同工序段的工件对缓冲区资源争夺而导致严重连续阻塞对进程的影响,保证能够顺利进行排产过程.具体步骤如下.

步骤1依据历史生产数据建立马尔可夫状态矩阵.

取单位时间段t′为全部工件在该工序的工位上加工时间中位值,建立在t′内可重入工序段的首道工序Oj(j=ru)中各工位转移概率矩阵Py(y=1,···,Mru),该矩阵用于预测对应缓冲区Bru资源释放概率,其中

可重入工序Oru中的工位在单位时间t′内有工件完工并移出,使得存放在缓冲区Bru中待加工的工件能够进入该工位进行加工,Bru中的缓冲车位得到释放,故以上4种概率可以被视为,在4种情况下时间段t′内缓冲区车位能否被释放的概率.

步骤2判断t时刻启动马尔可夫预测运算.

当运行状态如图5所示时,如果满足条件1–5,则执行步骤3,否则终止后续操作.

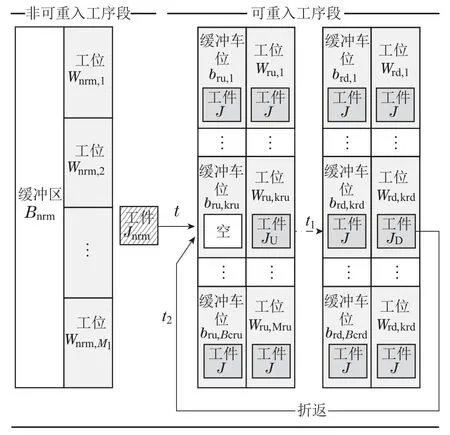
图5 t时刻运行状态示意图Fig.5 Diagram of workshopstate at time t

条件1: 非可重入工序段中存在将要进入Bru的完工工件Jnrm.

条件2:Bru中仅剩一个缓冲车位空闲,即=Bcru-1.

条件3: 可重入工序段首道工序Oru中的全部工均为被占用状态.

条件4: 依据工艺流程,在可重入工序段末道工序Ord中存在需折返并再次遍历可重入段的工件.

条件5: 条件1–4均满足的基础上可重入工序段首道工序Oru中最先完工JU的完工时间小于等于末道工序Ord中最先完工JD的完工时间t2,则继续执行步骤3,否则执行步骤4直接预留缓冲区.

在图5中,t1(t1≥t)为可重入工序段首道工序Oru中最先完工的工件JU离开Oru的时间,由于可能存在阻塞现象,t1大于等于;t2为可重入工序段末道工序Ord中最先完工的工件JD离开Ord的时间.

步骤3启动马尔可夫预测运算,预测缓冲区资源释放概率.

在t时刻采用马尔科夫链计算未来t2时刻工位上加工工件发生变化的概率向量[P1P2].通过计算得出t2时刻P2,即等价于Bru的缓冲车位释放的概率,进而动态判断Bru剩余缓冲车位是否为JD预留,降低因工件Jnrm争夺缓冲区车位而产生死锁现象的概率.

通过概率统计的方法计算从第1个工件投产运行到t时刻时,单位时间t′内工位上加工的工件变化的概率向量S0,即

式中:a1与a2均为统计得出,a1表示从0到t的时间段内,中未改变加工其他工件的单位时间段t′的数量与包含t′总数量的比值;a2表示从0到t的时间段内,中改变加工其他工件的单位时间段t′的数量与包含t′总数量的比值,即被不同工件占用的概率.

将S0代入式(21)计算在t2时刻工位上加工的工件变化的概率向量Sv,即

式中v表示从计算t时刻到未来t2时刻的时间段内包含t′的数量.

步骤4根据计算结果判别是否预留.

如果P1≥P2,则为将要折返工件预留缓冲车位,禁止来自非可重入工序的工件Jnrm进入可重入工序段;如果P1

当P1较大时,表示在未来t2时刻工位一直处于被同一工件占用,加工不同工件的概率较低,即在t2之前Bru中存放工件进入前道工序Oru的工位概率较低,Bru的缓冲车位难以被释放.若在期间允许非可重工序段中先完工的工件Jnrm进入Bru中,抢占了缓冲车位,会引起阻塞现象,Ord中先完工工件JD滞留在工位上.如果Ord中的所有工件都需要再次遍历可重入工序段会引起连续的生产阻塞现象,最终可能导致死锁现象发生.

步骤5依据判断结果,执行为即将重入工件预留缓冲区剩余车位操作,如图6所示.

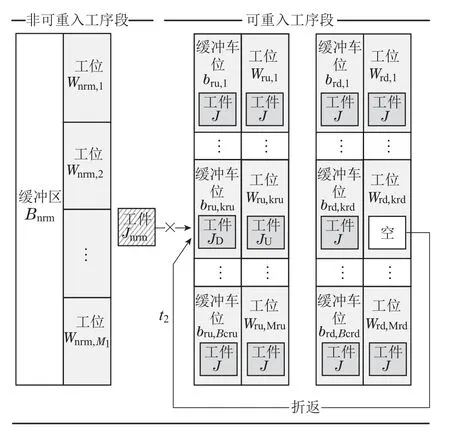
图6 折返执行可重入工序的工件进入预留缓冲区示意图Fig.6 Diagram of the reentrant Job entering the reserved buffer parking space

3.2 基于高响应比优先算法的局部指派方法

不同的局部指派方法也会影响死锁现象出现的概率的值,以基于短作业优先算法(shortest job first,SJF)的局部指派方法为例: 在生产过程的初期,根据短作业优先规则,缓冲区待加工队列中,依据工艺流程拥有更短剩余加工时间的工件具有更高优先权,不易出现阻塞现象(一般情况工件的工艺流程中工序较少剩余加工时间也越少),但随着生产进程的推进,该类工件依次完工下线,在生产线中剩余加工时间长、需多次执行可冲入工序的工件占比增多,由于缓冲区资源受限,在生产线中易发生生产阻塞,故死锁现象出现的概率也可能随之增大.

高响应比优先算法(highest response ratio next,HNNR)作为局部规则既考虑作业的执行时间也兼顾了作业的等待时间,综合了短作业优先算法和先到先服务算法(first come first service,FCFS) 的特点.基于高响应比优先算法的局部指派方法属于一种非抢占式优先权调度方法,高响应比是指作业等待时间与未运行时间的比值,一旦把工位分配给缓冲区待加工队列中具有最高优先权(比值)的待加工任务,则该加工任务便一直执行下去直至完成,定义如下.

系统运行到t时刻时有

其中: 式(22)中TW表示Ji在当前所在的缓冲区中等待加工的时间;式(23)中TR表示Ji依据其工艺流程FLi执行加工过程的剩余的加工时间;式(24)KR表示此刻Ji对应的响应比值,且比值大于等于1.

基于高响应比优先算法的局部指派方法具有以下特点: 1)当工件在待加工队列中等待相同时间时,具有越短剩余加工时间的工件优先权越高,即有利于短作业;2)当在等待加工队列中的工件具有相同的剩余加工时间时,工件的等待时间越长优先权越高,即先进先出;3)工件的优先权会随着其在待加工队列中等待时间的增加而增大,如果工件等待时间较长,则工件的优先权受等待时间影响更大,优先权随之增大,便有利于长作业.

因此,该方法通过计算和比较工件的响应比来确定待加工队列中工件的指派优先权,即考虑短作业又考虑工件的抵达顺序,同时又不会使得部分工件因长时间等待而无法进入工位加工,是一种折衷的局部指派方法.

3.3 DBRMMC的改进

DBRMMC中采用马尔科夫链进行预测运算,由于概率统计误差、计算误差等原因,通过预测模型所计算出的概率可能出现偏差,会导致Jnrm进入缓冲区Bru,抢占唯一资源,面对复杂度较高的排产过程,即使采用了DBRMMC方法排产过程依旧可能产生死锁现象.为避免此类预测偏差的出现,引入自适应阈值二值化改进DBRMMC方法,提出一种DBRMMC方法的改进方法IDBRMMC,为计算出的预测结果进行偏差补偿.

在步骤4中,若判断结果为P1

如果P1>P2且r1>α,不必对步骤4的结果进行偏差补偿,则缓冲区Bru剩余车位不为JD预留;

如果P1>P2且r1≤α,需对步骤4的结果进行偏差补偿(即Jnrm不进入Bru,剩余缓冲车位为JD预留).

当α=1时,表示Ord中的工件依据工艺流程全部需再次遍历可重入工序段,而r1因其取值范围一定小于α,所以即使当前时刻的预测结果出现偏差,也可以为即将折返的JD预留缓冲区剩余车位,因此,该方法能够避免预测偏差.

4 仿真实验

采用某客车生产企业的车间实例数据,对DBRMMC方法的运行过程进行分析,分别对不同规模的数据建立多组仿真方案,进行仿真实验.由于目前对于RFFLBS问题的研究仍处于初始阶段,针对该类问题的研究很少,尚无RFFLBS问题的标准算例.本文的测试用例来自于某大型客车生产企业,采用其涂装车间多遍贴彩条工序段的生产数据来构建,规模与取值均基于实际生产.

4.1 构造仿真数据

客车制造企业的客车涂装车间工序段包括“粘贴彩条模具”、“车体喷绘上漆”、“车身烘漆”工序,由于每遍彩条只能喷涂一种颜色,若客车涂装图案具有多种颜色则需多次喷漆和烘烤,即有有限缓冲区的特征也有存在可重入工序的工艺流程.

涂装车间工作人员会根据彩条的模板对不同车体喷绘的图案分解成多种颜色,依照工艺流程,经过多遍喷绘形成车体图案,不同车型因喷漆面积、彩条复杂程度等原因在同一道工序加工工时不同,客车在每道工序的加工时长在5∼45 min之间.同时,为了提高生产效率,减少客车在不同工位间的转运时间,“粘贴彩条模具”和“车体喷绘上漆”在统一个工序的同一个工位进行加工.

因此构造仿真数据共包含3个工序,即{O1,O2,O3},其中{O2,O3}模拟涂装车间的可重入工序,3个工序的并行工位数Mj均为3,3个工序分别拥有对应的缓冲区,即{B1,B2,B3},其中{B1}为无限缓冲区,{B2,B3}为有限缓冲区,缓冲车位数量分为Bc2=2,Bc3=3.

4.2 排产评价指标

1)最大完工时间.

式(26)表示完成全部加工任务时间,即所有工件依据工艺流程,完成最后一道工序的加工任务的完工时间中最大值.

2)总工位加工空闲时间.

式中TWT表示生产线中包含的全部工位的加工空闲时间之和,即工位加工第1个工件的开始到最后1个工件的完工期间的空闲时间.

3)总工件阻塞时间.

式中TPB表示所有工件在加工完成后,滞留在工位的时间之和.

4)总设备利用率.

式中FUR表示生产线中包含的全部工位的总设备利用率,即全部工位的有效加工时间与全部工位被占用时间之比.

5)出现死锁现象概率.

式中DLP表示E次仿真实验中死锁现象的概率.

4.3 排产结果仿真与对比分析

4.3.1 实例分析DBRMMC方法运行过程

首先采取一组数据进行测试并举例分析,其中工件总数n=15,即投产客车数,对应工件的重入次数{rts1,rts2,···,rts15}={5,5,4,4,4,4,3,3,3,3,3,3,2,2,1},采用基于先到先服务(FCFS)算法的局部指派方法.具体工艺流程如图7–8所示,加工时间如表1所示.

表1 工件遍历各工序时的加工时间(单位: min)Table 1 The processing time of the job in the process(min)

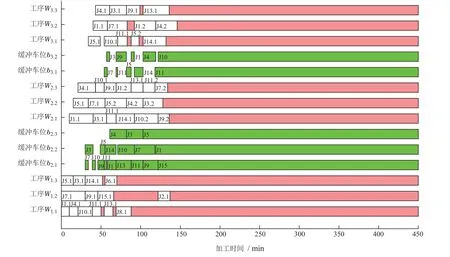
图7 当出现死锁现象时排产结果甘特图Fig.7 Gantt chart when deadlock occurs

图7是未采用DBRMMC 方法的RFFLBS 排产结果,图8是采用DBRMMC方法控制工件局部指派过程的RFFLBS排产结果,图7–8中Gantt图的横坐标是时间轴,纵坐标表示的是每个工序的工位以及每个缓冲区的车位.图中绿色表示客车在缓冲区停留时间,红色代表加工客车滞留在加工工位上的阻塞时间.

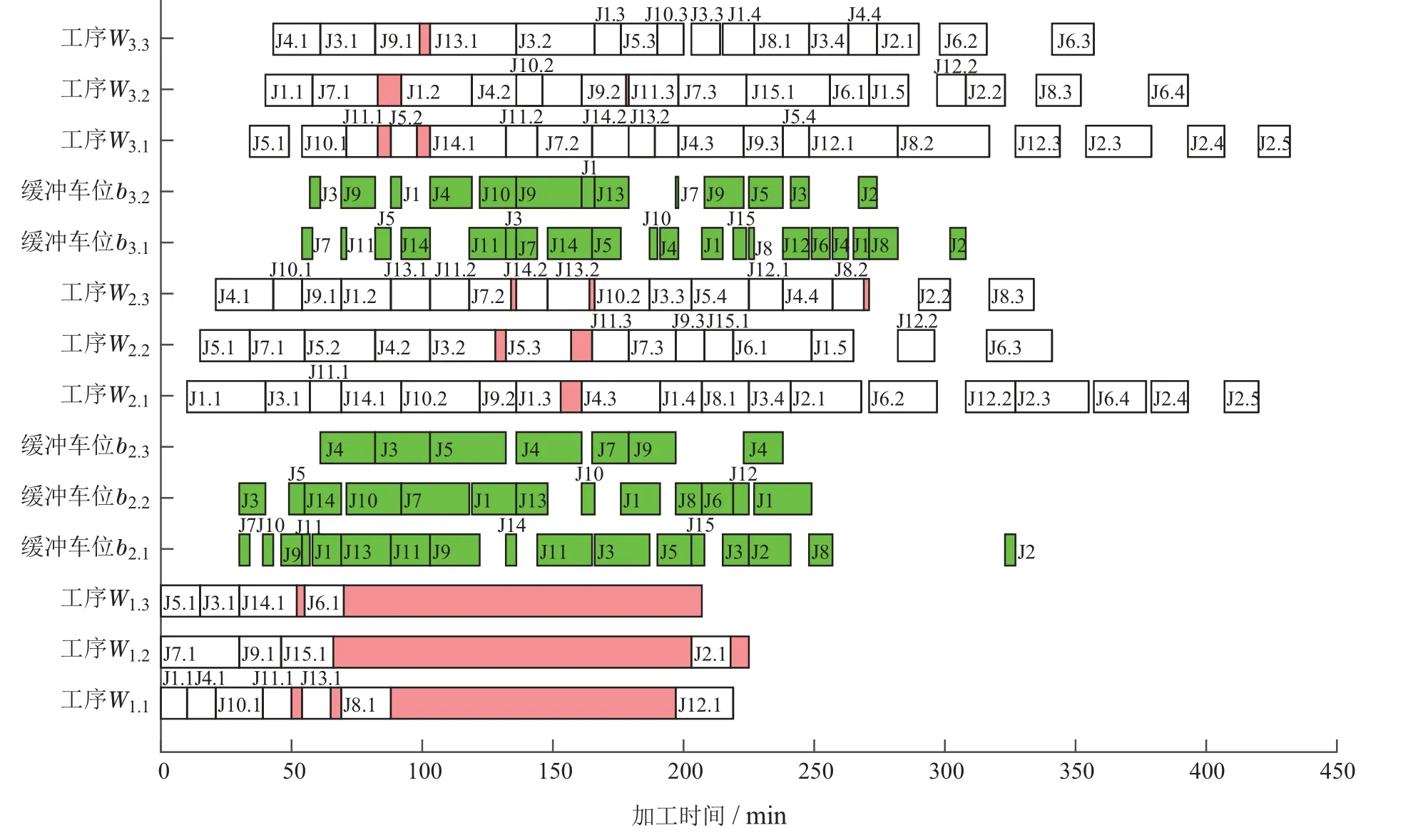
图8 加入方法后无死锁现象排产结果甘特图Fig.8 Gantt chart without deadlock after using DBRMMC

如图7所示,t=122时,工件J6,J8和J15已经完成在O1中的加工任务,准备进入可重入工序O2的缓冲区B2,B2中存放着工件{J1,J5},B2的容量Bc2=3,B2中有且仅有一个空闲缓冲车位,O2中的工位均处于被占用状态,在O3的工位上存在将要折返执行O2的{J4,J13,J14},O2中最先完工的J3的预计完工时间C3,2,2=128小于O3中最先完工的J14的预计完工时间C14,3,1=132,满足DBRMMC方法步骤2中启动马尔可夫链预测运算及执行后续预留判断步骤的条件.

假设在t=122 时不启用DBRMMC方法,当t=132时,在工位W3,1中完成了加工的J14,根据其工艺流程需要折返进入B2中,由于在此之前没有为J14预留B2的容量,在t=122时,B2已经被占满,所以J14滞留在W3,1中,发生生产阻塞,B3中的工件无法进入O3中进行加工.随着时间推移,工件{J13,J4}因B2已经被占满无法折返滞留{W3,3,W3,1}.当运行到t=148时,所有工件都被阻塞在当前位置上,这种严重阻塞的情况无法随着时间自解阻塞.从t=122时开始出现前文第1.4节中的死锁现象事件所描绘的场景,整个生产进程完全停滞,即出现死锁现象.

如果在t=122 时启用DBRMMC 方法,图8所示,马尔可夫链预测运算得出概率向量

W2,2上有工件完工并移出的概率P2=0.785621143大于无工件完工并移出的概率P1=0.214378857,依据步骤3中的判别条件为J14预留B2容量,令工件J15在工位W1,2中等待,当t=132 时,工件J3进入预留缓冲车位b2,3中,避免了死锁现象的出现,保证排产顺利进行,故采用DBRMMC方法干预工件在缓冲区的指派过程,可以减少死锁现象的发生.DBRMMC中采用马尔科夫链进行预测运算,由于存在概率统计误差、计算误差等原因,因此通过预测模型所计算出的概率可能出现偏差.

4.3.2 IDBRMMC方法降低死锁现象出现的概率仿真结果与分析

共设计7组仿真方案:方案1采用传统的排产方法,默认采用FCFS先到先服务调度算法进行局部指派;方案2在方案1的基础上加入DBRMMC方法;方案3在方案2的基础上引入补偿措施,这3组方案侧重于讨论DBRMMC方法以及加入偏差补偿对死锁现象的影响;其余4组方案分别引入基于SJF短作业优先算法的局部指派规则以及基于RHHN高响应比优先调度算法局的部指派规则,并测试DBRMMC方法在不同的局部指派规则下对于RFFSP排产过程中降低死锁出现概率的效果.仿真方案信息见表2.

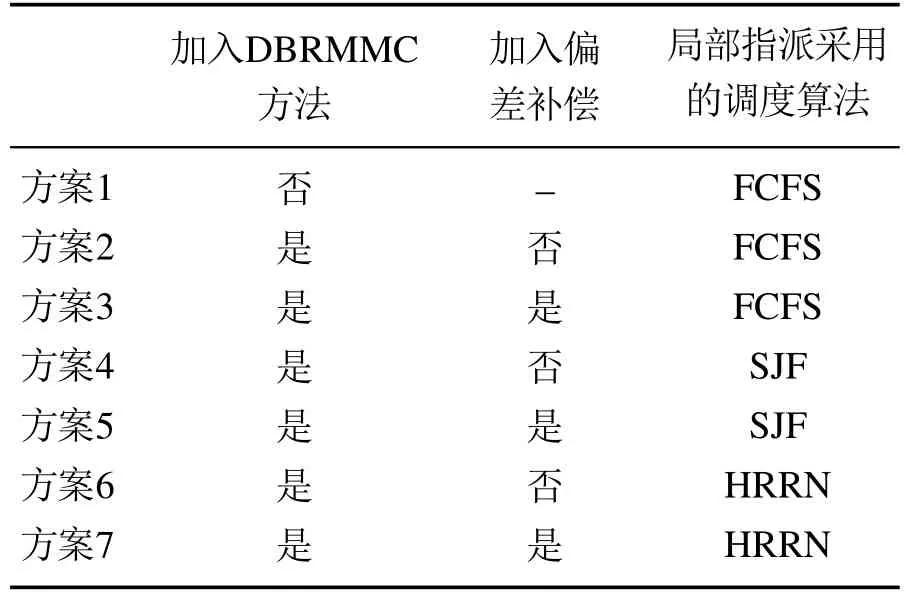
表2 仿真方案信息表Table 2 Simulation scheme information table

针对7组方案采用不同数据规模(投产工件数)进行仿真实验,在相同投产工件数情况下,依据不同重入次数的工件数量的差异构建多个仿真实例.设计统计变量Po,表示每个仿真实例中可重入工件占投产工件数的比例,如式(31)所示,该比例增加则表示可重入工件数量的增多.每个实例分别进行30次仿真实验,每次随机生成工件的上线序,工件在工位上加工时间采用10到30之间随机数,统计7组方案出现死锁现象的次数LN和死锁现象出现的概率PL,结果表2所示.

如表3所示,总投产工件数n=10时没有出现死锁现象,投产工件数量增加死锁现象出现.总投产工件数n=15时,方案1由于没有采用DBRMMC方法,随着具有可重入工序的工件数占总投产工件数比例Po增加,死锁概率PL由10.00%增长到26.67%.若总投产工件数量n增加,死锁概率PL也会增大,n=50时实例L和实例M的死锁概率PL=100%.故随着投产工件总数、可重入工件数在总工件数占总投产工件数比例的增加,死锁现象出现的概率不断增大,即随着加工任务的需求产能增加,对缓冲区资源的竞争愈发激烈,如果不采取一定的措施,排产过程将无法正常进行.

表3 不同数据规模的加工任务下RFFLBS过程中出现死锁现象及概率统计表Table 3 The number of occurrences of deadlock and the probability of occurrence of deadlock in RF-FLBS process under different data scale processing tasks

引入DBRMMC方法的方案2对比方案1,当投产工件数n=20时,实例G中具有可重入工序的工件数占总投产工件数比例P=30.00%的情况下,方案2的死锁概率PL2,20,G=3.33%比方案1降低30.00%;当实例I的P增加到80.00%时,方案2的死锁概率PL2,20,I=13.33%比方案1降低53.34%;投产工件数量n增加到50时,实例M的死锁概率达到了100.00%,排产无法进行,方案2死锁概率PL2,50,M=36.67%,死锁概率相较下降63.33%;投产工件数量n增加到100时,实例O采用方案2的死锁概率PL2,100,O=46.67%.可以看出DBRMMC方法的引入可显著降低RFFLBS排产过程中死锁现象出现的概率,在一定的需求产能范围内,具有可重入工序工件数量占总投产工件数的比例越大,投产工件数量的越多,效果更明显.

由表3数据可发现,即使引入了DBRMMC方法,实例I的结果仍有13.33%的概率出现死锁现象,而P相同的条件下,投产工件数n增加到100时,实例O概率会增加到46.67%,这是由于马尔可夫链预测缓冲区资源释放概率可能出现预测偏差,导致在RFFLBS排产过程中仍有死锁现象出现,且死锁现象出现的概率会随着需求产能的增大而进一步增大.对比方案3与方案2的平均死锁概率可知,加入偏差补偿改进的IDBRMMC方法能进一步降低RFFLBS排产过程的死锁现象出现的概率:当投产工件数n=20时,实例I采用方案3死锁概率为0.00%,投产工件数n增加到50时,实例M采用方案3比采用方案2死锁概率减少30.00%,而工件数n=100时,实例O采用方案3比采用方案2死锁概率减少40.00%,由此可见在一定的需求产能范围内,该方法可以基本消除RFFLBS过程中出现的死锁现象,引入偏差补偿措施会进一步提升DBRMMC方法在控制RFFLBS排产过程中出现死锁现象的概率的效果.

方案5采用基于SJF调度算法局部指派规则,在实例M中死锁概率为3.33%,低于方案3采用基于FCFS调度算法局部指派规则的6.67%,对比采用不同局部指派方法的方案发现,使用不同的调度算法控制排产过程的局部指派,对降低死锁现象出现概率也有一定程度的影响.方案7 采用IDBRMMC 方法,结合基于HNNR高响应比优先算法的局部指派方法,在不同投产工件数所有实例测试中死锁概率始终保持0.00%,即使投产工件数达到100依旧没有出现死锁现象,降低死锁概率的效果最优,方案7基本可以有效的消除LRFFLBS排产过程中的死锁现象.

对以上结果研究发现,采用IDBRMMC方法与基于高响应比优先算法(HRRN)的局部指派方法相结合的方案7(IDBRMMC-HRRN),可以有效的降低在RFFLBS排产过程中出现死锁现象发生的概率,避免死锁现象发生.在IDBRMMC方法为折返执行可重入工序的工件动态预留缓冲区容量的同时,使用基于HRRN调度算法的局部指派方法控制工件的局部调度,使具有较低复杂加工过程的工件优先加工,加速完成其加工任务,使之能够先完工下线,在排产过程中减少工件对缓冲区对资源的争夺,降低发生死锁现象的概率.

4.3.3 评价指标的结果对比分析

依据第4.3.2节分析,IDBRMMC-HRRN方法能有效的降低死锁现象出现的概率,但由于为折返工件提前预留缓冲区容量会导致来自非可重入工序段的完工工件阻塞当前工位上,引起阻塞时间的增加,进而可能使工件总等待加工时间变长,同时也可能会引起总完工时间增加和设备利用率降低等问题.

为综合分析IDBRMMC-HRRN 方法对整个排产过程的影响,本文采用多种评价指标对第4.3.2节中所设计的7 组方案的排产结果进行进一步分析,评价指标包括: 平均最大完工时间max、平均工位空闲时间、工件的平均滞留时间、平均设备利用率由于当出现死锁现象时,排产过程会发生停滞,因此无法获得上述指标,所以,仿真实验中若出现死锁现象的实验结果不记入统计结果中,具体数据如表4所示.

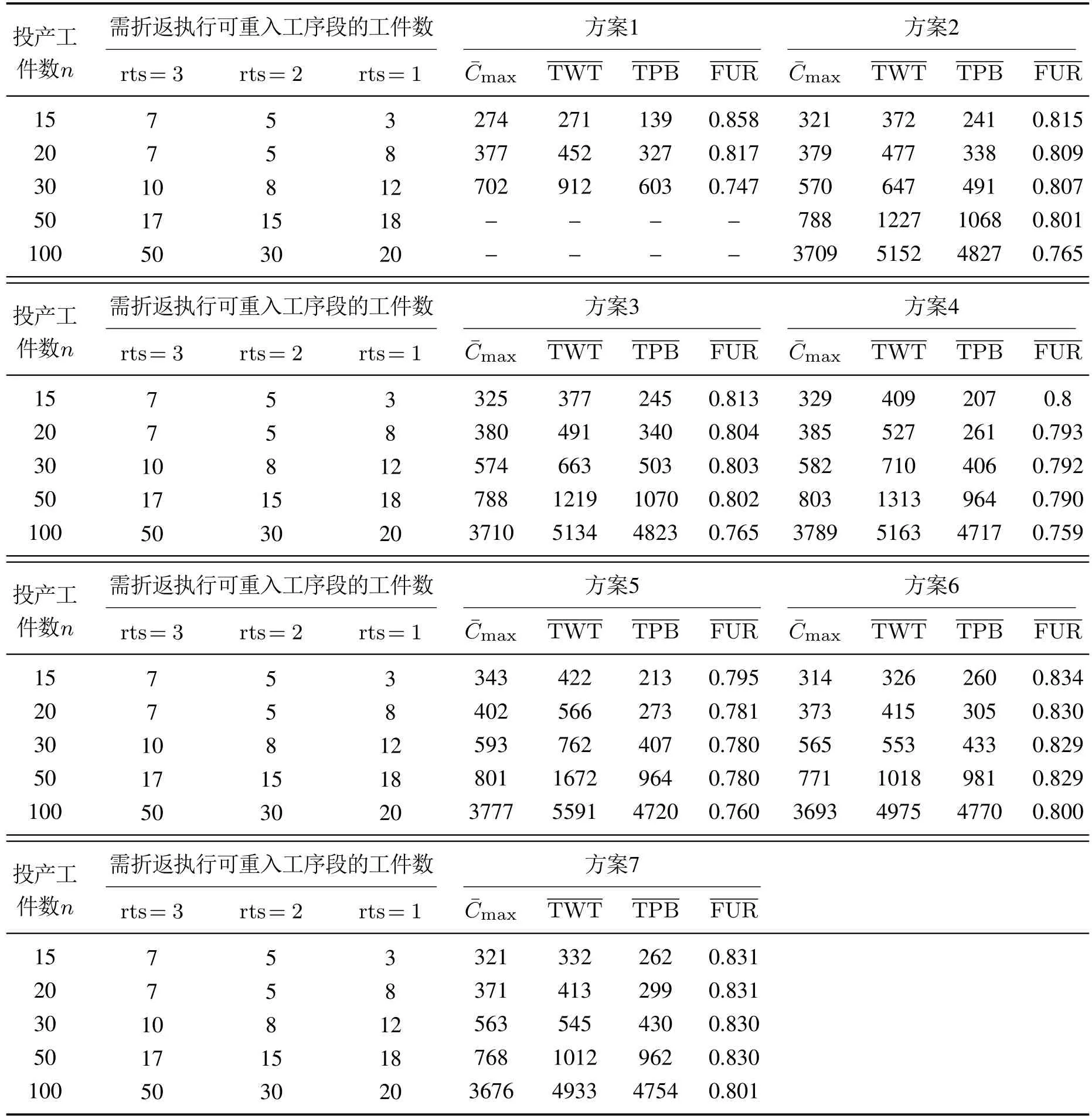
表4 不同求解方案下的评价指标Table 4 _Evaluation indicators under different schemes

可见DBRMMC方法对排产过程的影响具有一定的规律,为进一步研究在不同的投产任务情况下DBRMMC方法对排产结果的影响,绘制方案1、方案2的平均最大完工时间max与投产工件数关系曲线图如图9,其中各组数据可重入工件占投产工件总数采取相同比例,每组数据进行30次仿真实验并取平均值,相同投产工件数的数据,方案1与方案2采用相同上线序.

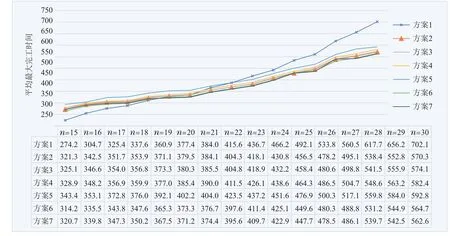
图9 不同投产工件数7组方案的平均最大完工时间Fig.9 The average maximum completion time of different number of jobs put into production in 7 groups of schemes

方案1与方案2的最大完工时间随投产工件数n增加而增大,n=15时方案1的平均最大完工时间max为274.2,采用DBRMMC方法的方案2的max=321.3比方案1增加47;当n=21时,方案1和方案2的max相等为384.1;若n继续增加方案2的max小于方案1,在n=30的情况下,采用方案2的max较方案1降低132.由此可知,DBRM-MC方法的引入会导致增大最大完工时间.但随着投产数的增加,即需求产能的增加,由于受到有限缓冲区的影响,生产阻塞情况随之增加,同时,随着执行可重入工序的工件数的增加,进一步加剧了生产阻塞,虽未出现死锁现象,但生产阻塞现象出现的机率增大导致自解锁时间增长,进而使得整个生产过程变缓.

因此从排产的局部指派过程看,DBRMMC方法的引入可以消除那些满足缓冲区预留条件的生产死锁现象,以增加局部阻塞时间的代价,提前破坏形成死锁潜在条件,换来整体生产进程的加快.

针对采用基于SJF局部调度方法的方案4和方案5,当n=22时,方案4 的max小于方案1,当n=24时,方案5的max小于方案1;针对采用基于HRRN局部调度方法的方案6和方案7,当n=20时,max小于方案1.偏差补偿措施的引入会小幅增加最大完工时间,但在不同的局部指派方法下引入偏差补偿措施对于评价指标的影响不同.

采用基于HNNR 算法的局部指派方法的方案7,当n=50 时,其=1012 比方案3 减少207,=962 比方案5减少2,方案7的各项评价指标为所有方案中最优,其设备利用率达到0.830,当n=100时,设备利用率较方案3和方案5分别提高了3.5%和4%.由此可知IDBRMMC 方法和基于高响应比优先(HRRN)算法的局部指派方法运用在LRFFLBS排产过程中不仅可以显著降低死锁现象出现的概率,同时,也可以有效的改善以最大完工时间为代表的各项评价指标,特别是在RFFLBS排产过程中的引入基于高响应比优先(HRRN)算法的局部指派方法,能够有效改善各项评价指标.

综合分析上述结果,在引入DBRMMC方法后,能够在求解RFFLBS排产过程中有效的降低死锁现象出现的概率,但同时也因局部的阻塞时间的增加,在处理小规模数据时对排产结果产生了不利的影响.加入偏差补偿措施的IDBRMMC方法可以进一步的降低死锁现象出现的概率,再结合基于高相应比优先算法(HRRN)的局部指派方法,可以更有效的降低死锁现象出现的概率,在处理小规模数据时,降低因引入IDBRMMC方法带来的局部阻塞时间增加对排产结果的影响,在处理大规模数据时可以获得更好的排产结果.

5 结论

本文以客车制造企业中存在的具有可重入工序的柔性流水车间有限缓冲区排产(RFFLBS)问题为研究对象,分析RFFLBS中阻塞与死锁现象的产生原因和影响,提出一种基于马尔可夫链的有限缓冲区容量动态预留方法(DBRMMC),该方法通过为折返执行可重入工序的工件提前预留缓冲区资源,减少对缓冲区资源的争夺,采用基于采用自适应阈值二值化算法的偏差补偿措施改进(IDBRMMC),再与基于高响应比优先(HRRN)算法的局部指派方法结合,进一步完善该方法,即改进的IDBRMMC-HRRN,保证排产过程顺利进行的同时获得更好的排产效果.该问题的研究成果可以为相关企业的生产运作过程提供切实的指导和帮助,提高企业现有资源的利用率.下一阶段的工作是引入强化学习对该求解方法进一步完善,优化针对更大规模生产线的执行效率,并引入全局优化算法进一步改善工位空闲时间、设备利用率等评价指标,在保证排产能够顺利执行的前提下获得更优的排产结果.