基于整体辨识策略的非线性自适应控制方法
张政煊 ,杨翊卓 ,代 伟†,周 平 ,杨春雨
(1.中国矿业大学信息与控制工程学院,江苏徐州 221008;2.北京科技大学自动化学院,北京 100083;3.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110819)
1 引言
非线性系统的控制是控制理论与应用中的重要研究课题,在实际应用中非线性系统普遍存在,如煤炭洗选过程[1]、无人机姿态控制[2]、工业机器人操纵系统[3]等.尤其针对复杂工业过程,如冶金、选矿等,其大多是一个气、液、固多相共存的连续化复杂物质转化过程,不确定干扰众多,工况动态变化,难以根据其机理结构建立精确的数学模型[4].随着自动控制领域的专家和学者的不断研究,在模仿生物适应能力的基础上建立了自适应控制方法[5].自适应控制方法针对具有不确定性的被控对象,根据系统的变化自动调节控制器的参数[6].对具有复杂动态特性的非线性系统而言,建立精确且便于控制器设计的模型是其自适应控制的基础和亟待解决的关键问题.
近年来,控制领域的学者深入研究了复杂工况下的非线性系统的系统辨识及控制问题[7–9].随着神经网络可以任意精度逼近非线性函数的特性不断被推广,神经网络被认为是辨识非线性系统模型参数和优化控制的新途径.谭永红[10]提出利用Specialised learning算法在BP(back propagation)神经网络框架下对被控对象进行在线辨识和控制,实现自适应控制.上述方法利用神经网络辨识非线性系统时,其网络结构难以确定,参数迭代过程复杂,不利于在线辨识和控制器设计.
Chen和Narendra[11]首先提出了将一类离散时间非线性动态系统表示成线性模型与高阶非线性项(未建模动态)的组合模型.在此基础上,文献[12]采用径向基函数神经网络逼近输入–输出非线性模型,并利用李雅普诺夫分析方法证明了闭环系统中所有信号都是半全局一致最终有界.文献[13]研究了一种由改进的投影算法与基于BP神经网络的未建模动态估计算法构造非线性系统的交替辨识方案.文献[14]提出在交替辨识的估计模型基础上开发非线性自适应控制器,严格进行了稳定性及收敛性的分析,并放宽了系统零动态渐近稳定的条件,使得交替辨识非线性系统的方案在自适应控制中得到了推广.文献[15]在未建模动态的增长率不超过其数据向量所在的紧集的输入向量的假设下,将非线性系统表示为线性部分和未建模动力学的组合,利用ANFIS(adaptive-networkbased fuzzy inference system)对未建模的动力学进行了估计.在实际应用时,考虑到控制器采用其他控制策略如滑模控制器时,其抖振会扩大控制系统的未建模动态产生的影响,从而恶化系统的控制性能[16],一般直接使用离散时间的PI控制器设计虚拟未建模动态补偿的自适应控制系统.文献[17]利用前一时刻虚拟未建模动态可测的特点,采用虚拟未建模动态补偿的一步最优PI控制策略设计供水温度控制器,通过理论分析和半实物仿真实验结果表明方法的有效性.文献[18]提出了一种改进的非线性系统交替辨识的智能建模方法,采用带遗忘因子的递推最小二乘法辨识低阶模型的未知参数,然后利用随机配置网络进行估计高阶非线性部分.上述方法交替辨识非线性系统的组合模型,并设计带未建模动态补偿的非线性自适应控制方法.然而,交替辨识的模型参数[19]将产生计算损耗,且难以确保整体系统的残差收敛,进而影响自适应控制系统的性能.
本文针对基于交替辨识算法的自适应控制方法研究存在的非线性系统辨识精度低的问题,提出一种基于整体辨识策略的非线性自适应控制方法.首先,利用低阶线性模型与未建模动态项组成的模型类量化非线性系统,建立随机向量函数(random vector function link,RVFL)网络模型与量化后的非线性系统数学模型之间的等价关系,并融入权值偏差惩罚项,设计网络模型参数在线更新算法;其次,根据控制输出的一步预报的最小方差指标计算线性控制器参数,并利用未建模动态项的补偿抵消闭环系统中复杂动态的影响;最后,在数值仿真研究和工业应用仿真研究中与基于交替辨识算法的自适应控制方法对比,验证所提的非线性自适应控制方法跟踪控制和稳定控制能力的优越性.
2 被控对象描述
本文的被控对象为一类单输入单输出(single input single output,SISO)离散的非线性系统,即
其中:u(k)和y(k)分别是系统的输入和输出;f(·)∈R是未知的非线性函数;nA和nB为系统的阶次;原点是平衡点.由非线性系统的特性分析可知,y(k+1)与过去时刻的输入、输出数据存在某种映射关系,令
其中p=nA+nB+1.则式(1)中的非线性系统可由包含非线性系统当前及历史时刻的输入、输出p维向量X(k)表示,即
针对上述这一类非线性被控对象,控制目标是要求被控输出跟踪参考输入,参考输入往往在工作点附近.因此可将系统作简化处理,在工作点附近将被控对象线性化可以得到线性模型.简化后得到的工作点附近的线性模型使得系统部分动态特性的丢失,往往达不到理想的要求,有时甚至还产生振荡和发散.因此,可在工作点附近,将非线性系统表示为低阶线性模型和未建模动态的组合形式,且低阶线性模型用时延算子z-1的多项式A(z-1),B(z-1)表示,即
其中:ai(i=1,···,nA)和bj(j=1,···,nB)为非线性系统在工作点处的一阶Taylor系数;v([X(k)])是虚拟未建模动态项,v([X(k)])有界,即|v([X(k)])|≤M.
进一步变换可得
3 基于RVFL网络的非线性系统整体辨识策略
3.1 随机向量函数链接(RVFL)网络[20]
随机向量函数链接(RVFL)网络由Pao和Takefuji[21]于1992年首次提出,其主要特点是: 1)输入层权值和隐含层偏置在特定范围内随机选取,与基于梯度的学习算法不同,不需要事先预设定过多参数和耗费大量的时间使算法收敛;2)输入数据做非线性变换后的增强层与输入层共同连接至输出层,使得增强节点的计算分担更小,所需节点数更少.RVFL网络凭借离线建模速度快、泛化能力强的优点使其在非线性系统回归建模和控制问题中得到广泛应用[22].
给定N组离线数据集Z={x(k),y(k+1)},x(k)∈Rm,y(k+1)∈Rn,k=1,2,···,N.xi,yi分别为n维输入向量和m维输出向量,则具有L个隐含层节点,且激活函数为Sigmoid函数的RVFL网络训练所得的预报模型可以表示为
其中:ωj和bj为增强节点的输入权值和偏置;w1,i为直接链接的输出权值;w2,j为增强链接的输出权值;hj为激活函数,表示增强特征的非线性映射.
RVFL网络是在固定范围内随机分配隐藏层的权值与偏差后保持不变,在线学习中唯一不确定的参数就是最小二乘法求解的输出权值.为避免完全随机分配的输入权值与隐藏层的偏差值导致模型的性能和稳定性出现波动,本文将改进了输出权值学习的目标函数,提高了RVFL网络辨识非线性系统参数的准确性.
3.2 非线性系统整体辨识策略
针对交替辨识算法存在辨识误差限增长的问题,本文利用一种带有输出权值偏差约束的RVFL网络,提出一种具有数值稳定性的非线性系统辨识方案.设计思想是: 利用低阶线性模型的输出辨识RVFL网络的直链输出权值,即线性模型参数;根据网络的输出残差e′构建RVFL网络的增强链接.避免了交替辨识导致的误差限上升的风险,与交替辨识的方案对比如图1所示.
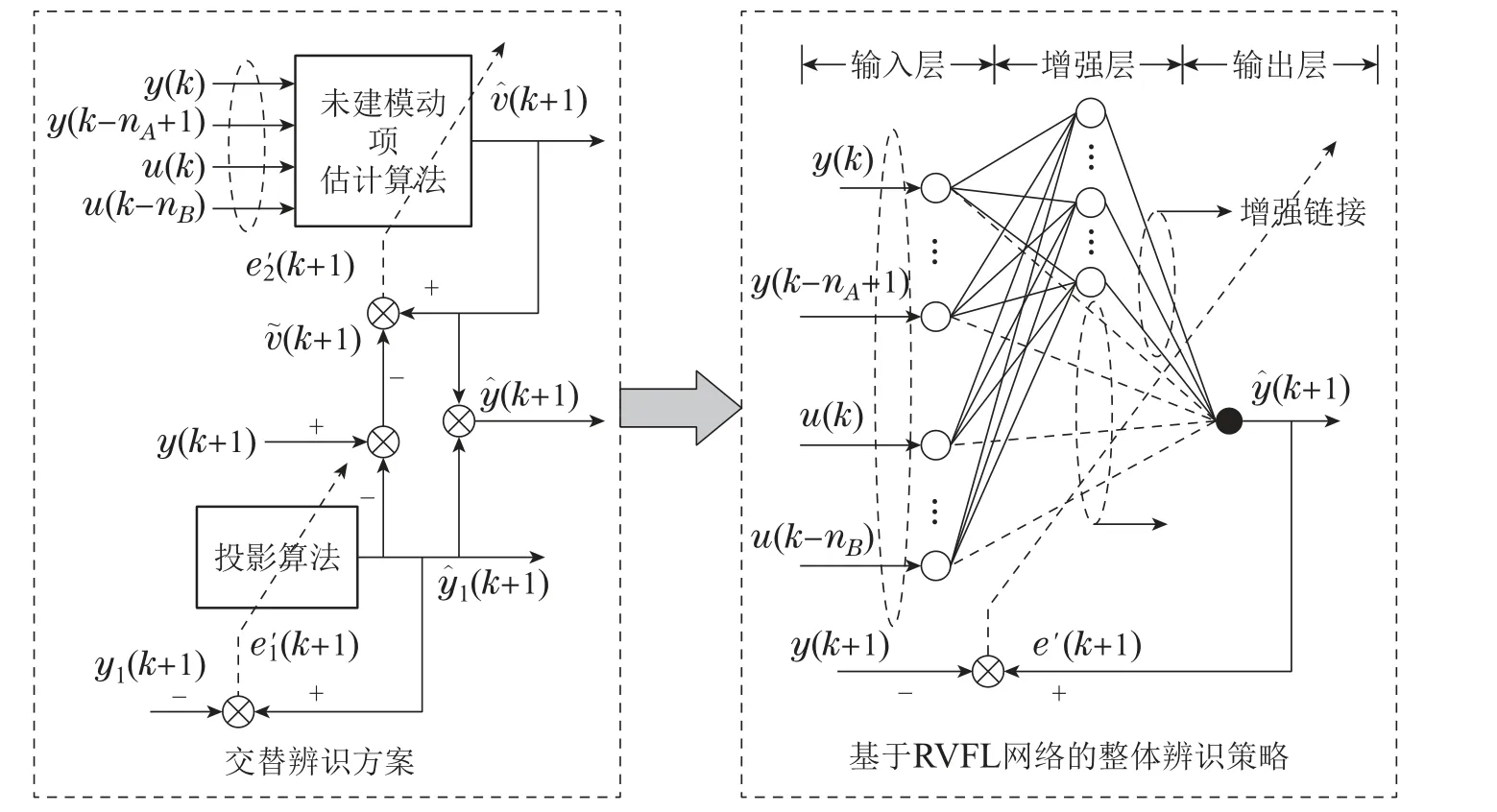
图1 交替辨识算法与基于随机向量函数链接(RVFL)网络辨识算法的对比Fig.1 Comparison between alternating identification algorithm and network identification algorithm based on random vector function linking(RVFL)network
对阶次如式(1)所示的非线性系统,将以[y(k)···y(k-nA+1)u(k)···u(k-nB)]作为RVFL网络输入,故将式(8)进一步改写为
基于RVFL网络的整体辨识策略通过网络输出残差逼近非线性系统,确保辨识结果收敛于非线性系统输出的实际值.
3.3 偏差约束的输出权值在线学习方法
非线性自适应控制的控制性能依赖于模型的精度.当系统输入发生变化时,实际非线性模型的参数也会发生变化.考虑到工业过程普遍存在的慢时变特性[23],故本文在RVFL网络模型参数在线学习中引入输出权值的偏差约束,以下给出RVFL网络输出权值的在线学习过程.
RVFL网络输出权值学习的目标函数[21]为
可视作非线性系统实际值与估计值之间的误差辨识准则.
在线学习中引入输出偏差惩罚项和正则化项后的目标函数[23]为
考虑到在实际非线性系统中,低阶线性模型与未建模动态项具有不同的特性,对RVFL直链与增强链接的输出权值偏差惩罚项的系数矩阵分开设计,定义如下:
式(12)对Wk求导得
注1由于RVFL网络具有万能逼近性[24],因此,只要选择合适的增强节点数,则对任意的正数ε>0,必存在一个理想的网络模型使得估计误差可以任意小,使估计误差e′(k)满足|e′(k)|=|y(k)-(k)|<ε.
4 非线性自适应控制器设计
4.1 未建模动态补偿的自适应PI控制
本文采用一种带虚拟未建模动态补偿的控制系统框架[24],根据线性模型参数设计线性控制器,同时,通过虚拟未建模动态项设计补偿器,消除虚拟未建模动态对闭环系统的影响.控制系统的结构如图2所示.
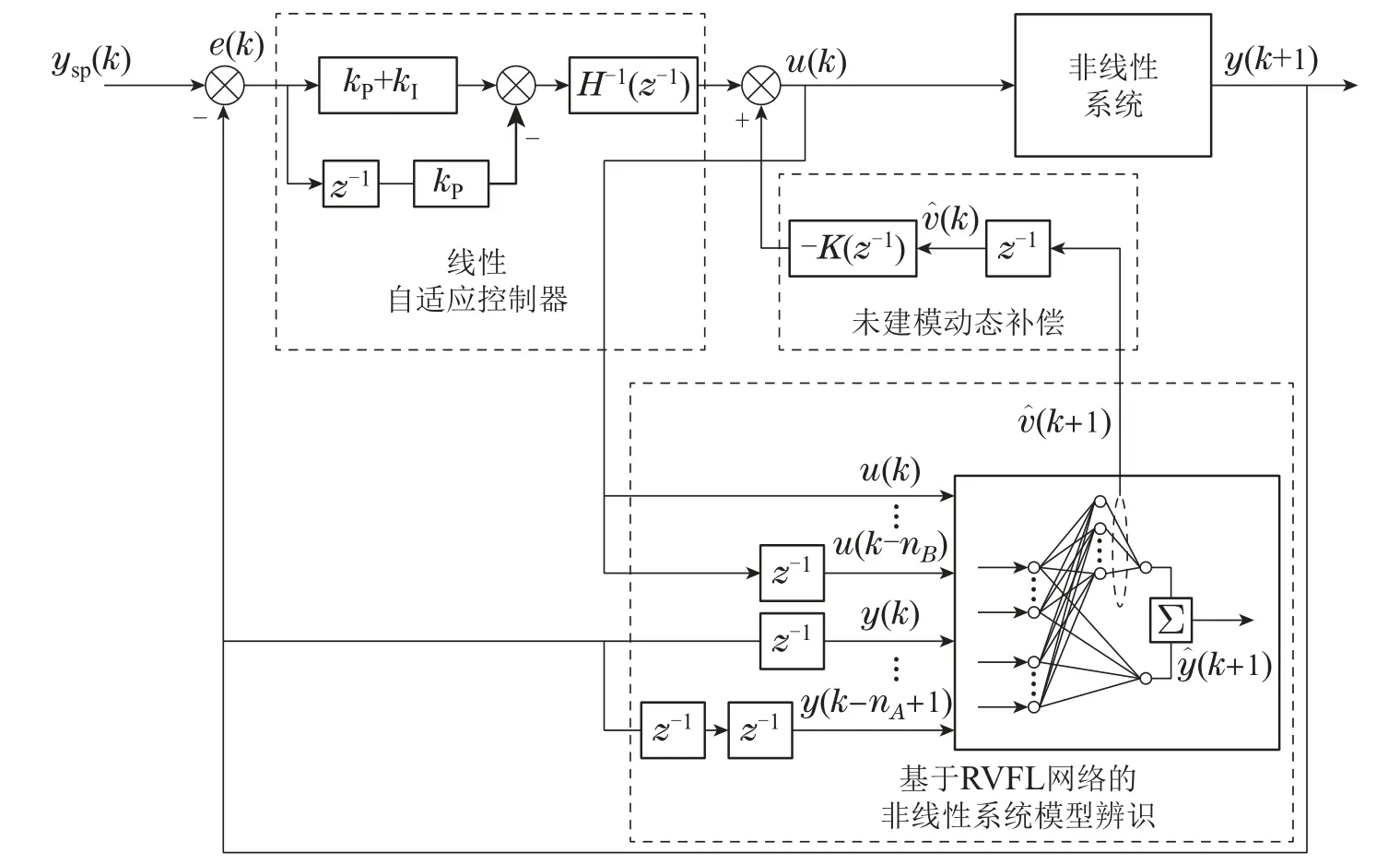
图2 基于RVFL模型的未建模动态补偿自适应控制结构图Fig.2 Structure diagram of adaptive control method for virtual unmodeled dynamic compensation
线性控制器采用PI控制器[25],进行移项及合并同类项得
其中:kP,kI为PI 控制器的比例、积分系数;K(z-1)和H(z-1)是z-1的多项式;e(k)为跟踪误差;e(k)=ysp(k)-y(k),ysp(k)为理想输出.
将式(15)改写为
其中:G(z-1)为z-1的时延算子G(z-1)=g0+g1z-1,g0=kP+kI,g1=kP.
4.2 基于RVFL网络模型的自适应控制方法
本文的自适应控制方法的基础是非线性系统的辨识.通过式(14)获得RVFL 网络的权值向量Wk,结合一步超前最优控制策略求解最优控制律[14].
将PI控制器的控制输入式(16)代入RVFL网络辨识所得的非线性系统式(11),并由(k)=W2THv可得到闭环方程为
为消除非线性动态项的影响,可令H(z-1)-B(z-1)K(z-1)=0,即可得到K(z-1)为
为求解G(z-1)引入一步超前最优控制策略,将下一时刻的输出y(k+1)与理想输出y∗(k+1)的误差满足方差最小情况时的输入看作是最优的控制输入,具体步骤如下:
步骤1设计未建模动态项补偿.引入Diophantine方程
对式(16)等式两边同乘以F(z-1),则有
其中P(z-1),H(z-1)均为关于z-1的加权多项式.
步骤2设计控制性能指标.定义广义输出误差为
定义性能指标为被控对象输出的理想误差eg×(k+1)的方差,即
步骤3求解最优控制律u(k).显然使得误差eg×(k+1)的方差最小时,使式(23)极小的最优控制.F(z-1)已知的条件下,G(z-1)由Diophantine 方程(19)唯一确定.将式(20)代入式(23),并令J=0,得到非线性系统的最优控制律为
由式(16)和式(24)可得,F(z-1)可通过如下对应关系求解:
根据Jury判据,需离线选择P(z-1)和Q(z-1)使得下式成立:
选定P(z-1)=1,通过式(20)(26)计算可得G(z-1),可得PI控制器参数如下:
为了消除未建模动态v(k)对闭环系统的影响,通过选定的Q(z-1),由式(18)(21)(25)以及式(27)可知选择(z-1)应满足
因此,PI控制器式(15)中的K(z-1)可表示为
4.3 稳定性及收敛性分析
以下将给出本文所述的自适应控制方法的稳定性分析.
引理1根据RVFL网络模型参数描述的非线性系统(11),系统的输入输出动态特性方程如下,式中省去了多项式z-1,即
采用类似于文献[25]的方法可证明引理1.
定理1假定系统(4)满足如下假设条件:
1) 系统的未建模动态项v(X(k))有界;
2)b0>bmin>0,B(1)0;
3) 选择合适的Q(z-1)使其满足
则有
a) 闭环系统有界输入和有界输出(bounded input bounded output,BIBO)稳定,即
b) 当k→∞时,系统的跟踪误差有界.即
其中:ysp(k)为系统的期望输出;ξ=2εδM,ε为任意小的正数,δ为大于0的常数.
由文献[23]得证定理1条件3)的a)项成立.
定理1条件3)的b)项证明如下.
证当k→∞时,有
4.4 算法步骤
本文的非线性自适应控制方法的步骤如下:
步骤1初始化RVFL网络.设置RVFL网络的最大节点数和网络初始残差值,计算直链的输出权值;
步骤2构建RVFL网络离线模型.不断地加入增强节点逼近非线性系统的输出,若输出误差小于设定的残差值,记录下离线训练所得的网络输出权重,作为在线学习过程的初始权重,并执行下一步;
步骤3初始化线性控制器与未建模动态补偿器.根据网络的初始权重、离线选择的Q(z-1)并计算F(z-1),由式(21)(24)和式(29)–(30)计算线性控制器kP和kI的初始值,根据式(32)计算未建模动态补偿器增益K(z-1)初始值;
步骤4在线采集被控制系统的输入输出数据.构建k时刻的网络输入,根据式(14)在线学习k+1时刻的网络输出权值Wk;
步骤5根据k+1时刻的直链与增强链接的输出权值,按照步骤3的过程调整k+1时刻的线性控制器参数和建模动态补偿器增益;
步骤6若模型精度不能达到性能要求,则调整残差容忍度的设定值,并返回步骤2,否则返回步骤4.
根据上述方法步骤进行仿真研究,并选取合适的输出权值惩罚系数C和输出权值偏差惩罚项系数k1和k2以及时延算子多项式P(z-1)和Q(z-1).
5 数值仿真研究
为验证本文提出的控制方法的有效性,考虑如下的离散时间非线性系统:
显然,系统的阶次nA=2,nB=1.系统的参数多项式为
非线性系统数值模型的未建模动态项为0.02 sin(0.5y(t)u(t)+2y(t-1)u(t-1))全局有界,满足定理1的条件1).
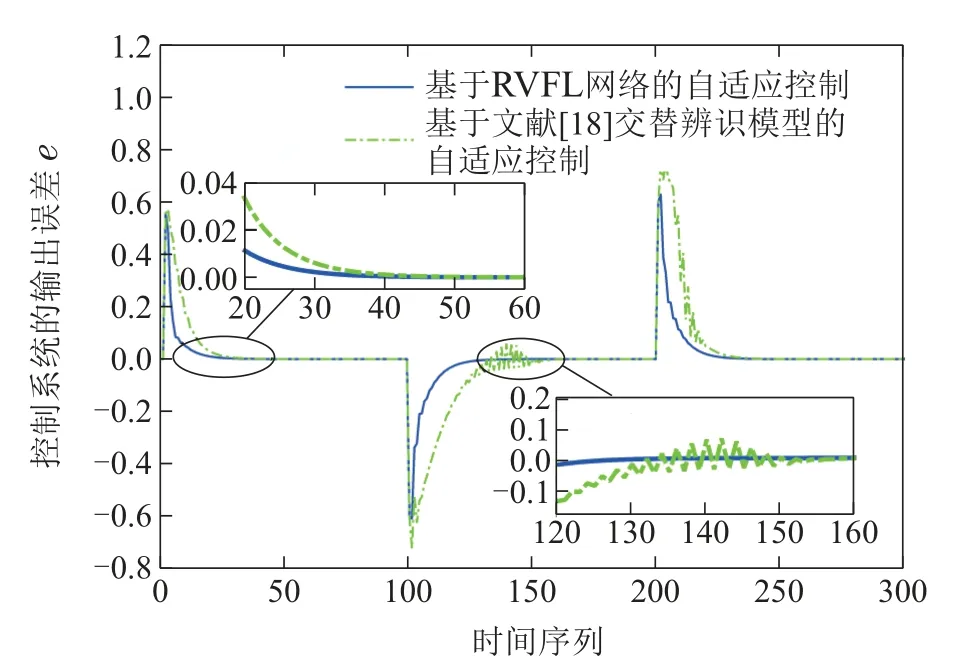
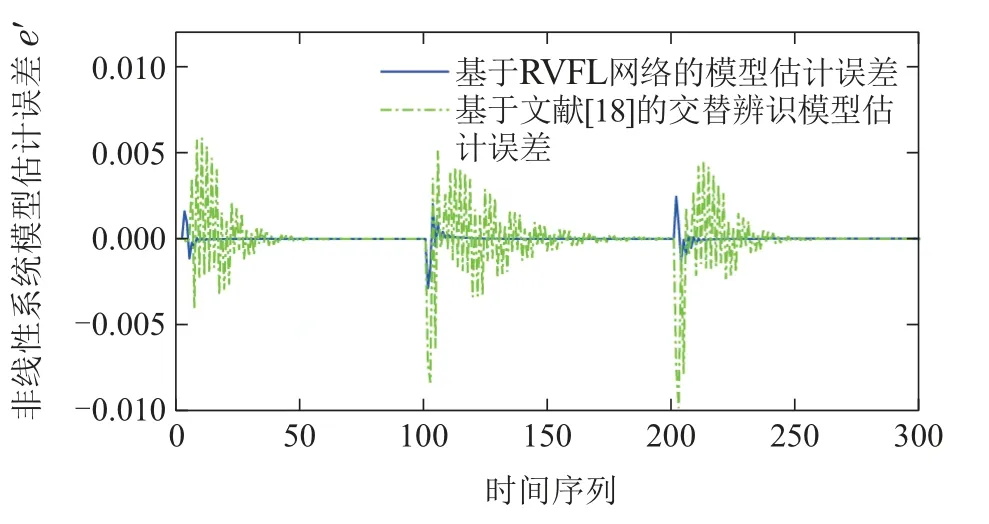
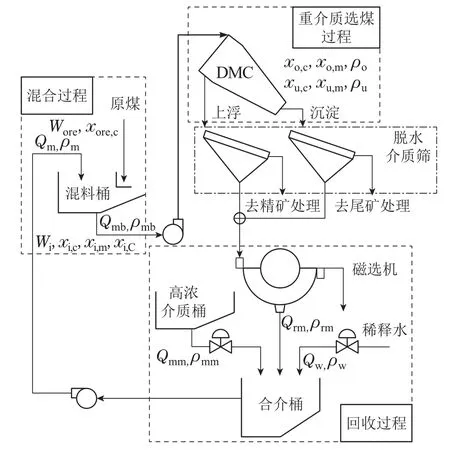
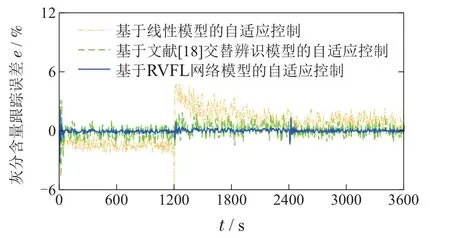
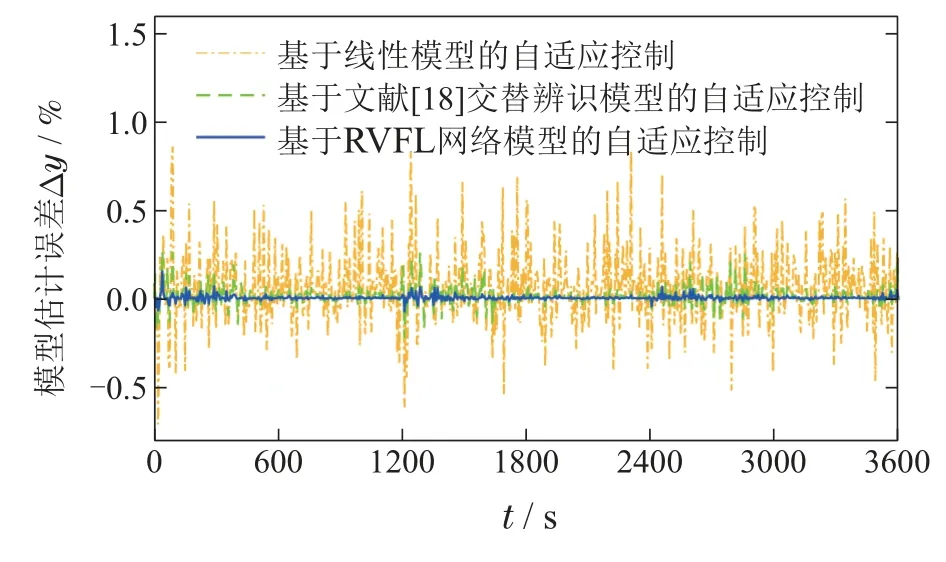
控制目标是: 使得系统输出y(t)分别跟踪参考轨迹w(t)=2(0≤t≤100,200 基于整体辨识策略的非线性自适应控制方法中包含若干重要的参数,令离线数据的维数N=5000组,设置网络的最大节点数Lmax=1000,网络的残差为4.5×e-3.离线选择时延算子多项式P(z-1)=1,Q(z-1)=0.2. 在仿真中,采用设定值跟踪均方根误差(root mean square error,RMSE)作为控制的性能指标,记作AC(adaptive control)–RSME,采用非线性系统模型估计值与实际值均方根误差验证辨识算法的性能指标记作MI(model identification)–RSME,表达式如下: 可以看出,所提基于RVFL网络整体辨识策略的非线性自适应控制方法,能够对离散时间的非线性系统进行有效的控制.将基于投影算法和随机配置网络(stochastic configuration networks,SCNs)交替辨识的模型[18]应用于非线性自适应控制方法中与本文方法进行对比,仿真结果如图3–5和表1所示.相比较,所提方法的设定值跟踪性能更好,并且具有更好的动态跟踪和稳态性能.这是由于所提方法的辨识模型通过整体的非线性系统输出残差e′与设定的残差容忍度不断迭代计算,使得离线模型小于设定精度逼近数值模型(39).基于投影算法和SCNs的非线性自适应控制方法需要更长的时间达到满意的跟踪控制效果,且在设定值发生变化后的一段时间内仍会有较大幅度的跟踪误差,是由交替辨识的算法不能够保证对非线性系统模型的逼近性能导致的. 图3 基于不同模型自适应控制方法的输出Fig.3 Output of adaptive control methods based on different models 图4 基于不同模型自适应控制方法的输出误差Fig.4 Output error of adaptive control methods based on different models 图5 模型辨识误差对比Fig.5 Comparison of model identification errors 重介质选煤控制系统在实际生产过程中,主要是通过调整重介质悬浮液密度控制分选效果,而灰分含量是评价炼焦精煤产品质量的重要的运行指标.利用式(4)的非线性模型描述重介质选煤灰分含量控制回路的动态过程,辨识此回路过程的线性模型参数和估计未建模动态项,并设计线性控制器和补偿器. 如图6所示,重介质选煤过程[26]主要涉及混料、重介质旋流器分选以及重介质回收,主要过程为:首先,将原煤与重介质悬浮液充分混合;其次,在重介质旋流器中分离混合矿浆;最后,回收稀释的重介质液.主要涉及的参数包括重介质悬浮液介质流量Qm,合格介质桶中加入水的密度ρw,回收矿浆中重介质的密度,向合格介质桶中加入高浓介质的密度ρmm,磁选机出口处重介质的密度ρrm,合格介质桶中重介质悬浮液的体积Vcor,加水阀门系数Cw,参考实际重介质选煤过程采用文献[24]的数据设计上述过程参数并搭建模型采集输入输出数据,具体如表2所示. 表2 重介质选煤过程工艺参数Table 2 Dense medium coal separation process parameters 图6 重介质选煤过程工艺流程图Fig.6 Dense medium coal separation process flow chart 令网络输入数据向量的维数N=6000,设置网络的最大节点数Lmax=1000,网络的残差容忍度为8.3×e-2.得到离线辨识的低阶线性模型参数如下: 将初始的控制信号重介质悬浮液的密度u(0)=1530 kg/m3;运行指标精煤灰分含量的初始值设为y(0)=14%.根据炼焦煤产品按照灰分指标的不同分级,验证本文方法在不同设定值工况下的跟踪控制性能,初始时刻精煤规格为3级,其他用炼焦精煤(14%);20 min时,调整为10级冶炼用炼焦精煤(10%);40 min时调整为6级冶炼用炼焦精煤(8%).给煤量为8 kg/s,同时设定[-1,1]的随机动态变化量,在此工况下对灰分含量进行跟踪控制. 设定值跟踪控制仿真的研究中基于不同模型的控制方法效果如图7–9所示.基于各模型的控制方法的性能指标如表3所示.本文方法中通过试凑法选择输出权值惩罚系数C=85,偏差惩罚项系数k1=104,k2=10-2. 表3 基于不同模型的灰分含量跟踪控制性能对比Table 3 Comparison of ash content control perfor-mance 图7 重介质选煤灰分含量跟踪控制输出Fig.7 Tracking control output of ash content in dense medium coal separation 图8 重介质选煤灰分含量跟踪控制输出误差Fig.8 Output error of ash content tracking control in dense medium coal separation 图9 重介质选煤灰分含量控制回路的模型估计误差Fig.9 Comparison of model identification errors 对比3种控制方法,其中基于交替辨识模型的自适应控制方法引入了未建模动态项的补偿,性能指标AC–RSME和MI–RSME优于基于线性模型的自适应控制方法.但交替辨识所得的模型无法保证收敛于实际的模型输出.而本文基于RVFL网络的非线性自适应控制方法,利用RVFL网络根据整体辨识策略迭代计算网络的增强节点参数,能够保证灰分含量控制系统的输出误差上界为ξ=2εδM.最后,得出对灰分含量设定值跟踪控制满意的输出. 本文提出了一种基于整体辨识策略的非线性自适应控制方法.主要贡献是: 1)针对低阶线性模型与未建模动态项的非线性系统组合模型,提出利用RVFL网络的直链与增强结构特性进行整体辨识;2)针对具有慢时变特征的非线性系统,提出一种输出权值偏差约束的在线学习方法;3)根据RVFL网络在线辨识的模型参数,设计未建模动态项补偿的非线性自适应控制方法.所提方法在数值仿真和工业应用仿真研究中验证了有效性和优越性. 针对实际应用中面临的潜在问题,需要进一步开展下列研究:1)实际应用中难以测量大滞后以及非高斯变量的统计特性,应考虑基于输出变量概率密度函数设计控制律;2)该方法依赖于模型的辨识精度,应结合实际生产过程建立具有鲁棒性的RVFL网络模型,克服离群点干扰.此外,未来在理论上考虑从放松未建模动态有界条件的方面开展工作.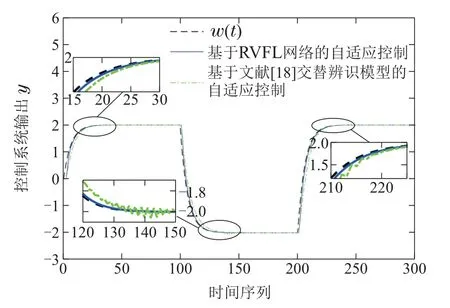
6 工业应用仿真研究



7 结论与展望

