网联车辆有限时间滑模预设性能队列控制
高振宇,孙振超 ,郭 戈,2
(1.东北大学秦皇岛分校控制工程学院,河北秦皇岛 066004;2.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110004)
1 引言
近年来,随着自动控制技术及通信技术的飞速发展,使得智能交通系统成为现实[1].其中,网联车辆队列控制,即驱驶车辆依照给定间距策略以较小车间距按队列行驶,被认为是智能交通领域中缓解交通拥堵、降低能源消耗、提高运输效率最有效的途径[2–4].由于侧重点的不用,涌现出越来越多的研究热点,如:通信拓扑的切换[5]、间距策略的选择[6]、队列稳定[7]、车辆动力学[8]等.伴随着新一代控制技术的发展,如何进一步提高队列系统性能既充满挑战又极具研究价值.
由于运行环境及车辆自身建模的影响,由风、路况等引起的外界扰动及模型不确定成为制约车队控制性能的重要因素.提高系统鲁棒性,有效缓解上述因素的影响,成为选择控制算法的前提.目前,滑模控制因其鲁棒性强的特点,使其在队列控制中得到广泛应用.文献[9]采用线性滑模理论,实现了含有参数不确定的队列控制.文献[10]基于PID滑模理论,实现了含有不确定的队列容错控制,获得了较好的稳态性能.然而,基于传统滑模的控制方案[9–10],只有当时间趋于无穷时才会获得期望的控制效果.近年来,为了提高收敛速度,文献[11]提出了一种积分滑模控制方案,通过引入跟踪误差的幂次项保证了有限时间队列控制.由于积分项的引入,该方案会增加系统的抖振.文献[12–13]设计了基于终端滑模理论的控制方法,保证了跟踪误差的有限时间收敛,同时减少了系统抖振.然而,文献[12]只适用于二阶队列系统,且文献[12–13]都无法保证队列的稳定性.
需要指出的是,上述成果只从稳态性能角度实现了队列控制,而忽略了超调量、收敛速度等瞬态性能.在实际应用中,队列目标能否成功实现,瞬态性能同样至关重要.比如,较快的收敛速度有助于提高控制系统的效率,但过快的收敛速度易导致超调量过大,降低系统性能,甚至导致系统不稳定.预设性能控制是一种可以兼顾瞬态及稳态性能的方法,通过保证跟踪误差始终保持在性能函数定义的边界之内,获得较好的收敛速度及稳态误差[14].文献[15–17]分别提出了一种基于预设性能控制的队列控制方法,保证了避碰、连通性以及跟踪误差的收敛性,获得了较好的瞬态、稳态性能.为避免跟踪误差因过大或过小而导致队列失败,文献[18–19]提出了基于预设性能的控制方法,保证了系统超调量始终在预设的范围内.然而,上述成果都存在一个保守性结论,即无法预先设置跟踪误差收敛到预设期望边界值的时间,进而导致给定控制方法无法保证跟踪误差在指定时间内收敛到预设范围内.此外,文献[20–22]研究了乘波体飞行器的预设性能控制,并提出了有限时间预设性能控制方法,但给定算法只能够保证跟踪误差在有限时间内收敛到预设区域,而不能保证闭环系统内所有信号都是有限时间稳定的,即所提算法无法保证闭环系统在明确可得的时间内达到稳态.
基于以上分析,本文针对含有未知扰动及模型不确定性的网联车辆预设性能队列控制问题展开研究,提出了一种基于改进滑模的有限时间预设性能队列控制方法.与已有文献相比,本文主要创新点总结如下:
1)与文献[15–19]相比,本文提出了一个新型预设性能函数,保证了跟踪误差可以在给定时间内收敛于期望的稳态误差带.此外,该性能函数只需较少参数便可调整跟踪性能.
2)为保证跟踪误差的有限时间收敛,结合预设性能控制,设计了一种基于改进滑模的队列控制算法.不同于文献[9–13],本文所提算法不仅保证了队列目标在给定时间内实现,同时改善了系统的收敛速度且保证了队列稳定性.此外,通过设计自适应律,解决了外界扰动及模型不确定性问题.
本文组织结构如下: 第2节给出问题描述及预备知识;第3节给出本文主要结果;第4节是数值仿真;最后进行总结.
2 问题描述及预备知识
2.1 问题描述
考虑一个行驶在直线路径上由领队车和N辆跟随车组成的车队,如图1所示.领队车运动学模型为
其中x0(t),v0(t)和a0(t)分别为领队车的位置、速度和加速度信息.
跟随车i(i∈1,2,···,N)的运动学及动力学模型描述为如下三阶非线性系统[23]:
其中:xi(t),vi(t),ai(t)分别表示跟随车的实时位置、速度和加速度;ui表示第i辆车的控制输入;ωi(t)表示由风、路况等引起的外部未知扰动;mi表示第i辆车的质量;Ξi=migbicosθi+mig sinθi表示道路坡度函数;θi表示道路的坡度角度;bi表示道路阻力滚动系数;g 表示重力加速度;τi表示汽车发动机时间常数;ρa表示空气质量;Cai表示空气动力阻力系数;Ai表示车辆横截面积.由于技术限制,τi,θi等参数无法精确获得,因此fi(vi,ai)为未知的函数.
受文献[19,24]的启发,将未知函数fi(vi,ai)写成如下形式:
其中:fi0(vi,ai)为已知项;∆fi(vi,ai)为不确定项.
基于式(2)(4)中的第3式可改写为
其中Di=∆fi(vi,ai)+ωi(t)表示作用到车辆i上的由未知扰动及模型不确定性引起的集总扰动.
假设1集总扰动Di是有界的,满足|Di|≤,其中是未知正常数.
注1由于车辆运行速度、携带能源及外界扰动能量的有限性,可知假设1是合理的.
为了提高队列的安全性及稳定性,本文采用恒时距间距策略.定义相邻车辆间距跟踪误差为
其中:Li为第i辆车的长度;∆i为车辆间最小安全距离;hi为车辆间行驶时距.
如文献[10,15–16]所述,非零初始误差会导致较大的瞬态发动机推动力及制动扭矩,甚至导致队列不稳定.为了消除非零初始误差对系统性能的影响,本文引入了一种改进的恒时距策略,即
其中πi是待设计的正常数.
经过计算得
这表明改进的间距误差的初始值恒为零,从而消除了非零初始误差的影响.
为方便后续控制器设计,经过计算,ei(t)的一阶和二阶导数如下:
2.2 控制目标
根据本文提出的控制问题及模型,考虑跟踪误差的收敛性、设计跟踪控制律,实现如下指标:
1)有限时间单车稳定性: 相邻车辆间的跟踪误差在有限时间内收敛到零附近的小邻域内,描述如下:
其中:Ti为跟踪误差收敛时间;ϵi为较小正数;
2)队列稳定性[10]: 跟踪误差不沿着队列向上游车辆传播,描述如下:
3)有限时间预设跟踪性能:对于给定的有限时间Tfi和约束条件,即
2.3 预备知识
引理1[25]对于系统=f(x),如果存在一个连续径向有界函数V(x),满足
引理2[25]对于系统=f(x),如果存在一个连续的正定函数V(x),在零附近的开区间U→R有:(x)+c(V(x))α≤0,其中:c>0,α∈(0,1),那么系统=f(x)是全局有限时间稳定的,并且有限时间T满足:
引理4[26]对于c>0,s≤c,p≥0,q>0,k>0,下列关系成立:
引理5[27]对于∀γ>0和χ∈R,下列不等式成立:
其中k=0.2785.
定义1[28]存在一个连续性能函数ρ(t),如果满足下述指标:
3 主要结果
针对控制目标,本文首先构建了有限时间性能函数,保证了约束满足,进一步提出了基于改进滑模的有限时间控制器,实现了有限时间单车稳定性及队列稳定性.本文整体控制算法设计结构如图2所示.
3.1 误差转换及滑模面的构建
为满足预设性能,根据定义1,本文设计了一种新型有限时间性能函数,即
注2当前大部分网联车辆预设性能队列控制研究中[15–17],为满足性能约束,采用如下性能函数:ρi(t)=(ρi,0-ρi,∞)exp(-ni1t)+ρi,∞.不难看出,上述性能函数是指数收敛的,在一定时间T内,ρi收敛到较小区域,可称之为近似稳态,但是该收敛时间T是无法精确获取的.相比而言,本文设计的性能函数ρi(t)可以在t→Tf时达到规定的界限值ρi(Tf),并且收敛时间Tf的具体值可以根据实际情况确定.此外,可以通过选择合适的ρi(Tf)和Tf的值来调整跟踪性能,以保证系统的暂态性能.
这里,直接根据误差约束(12)设计控制器会增加设计难度,为了解决该问题,引入下面的误差转换,将有约束的跟踪误差转换成无约束误差,即
在本文中,误差转换函数Γi(·)选择为
因此转换后的误差为
由于存在外部扰动、模型不确定以及性能约束,为了在有限时间内实现控制目标,基于上述误差转换,构建了一种基于改进滑模的控制算法.改进的滑模面设计如下:
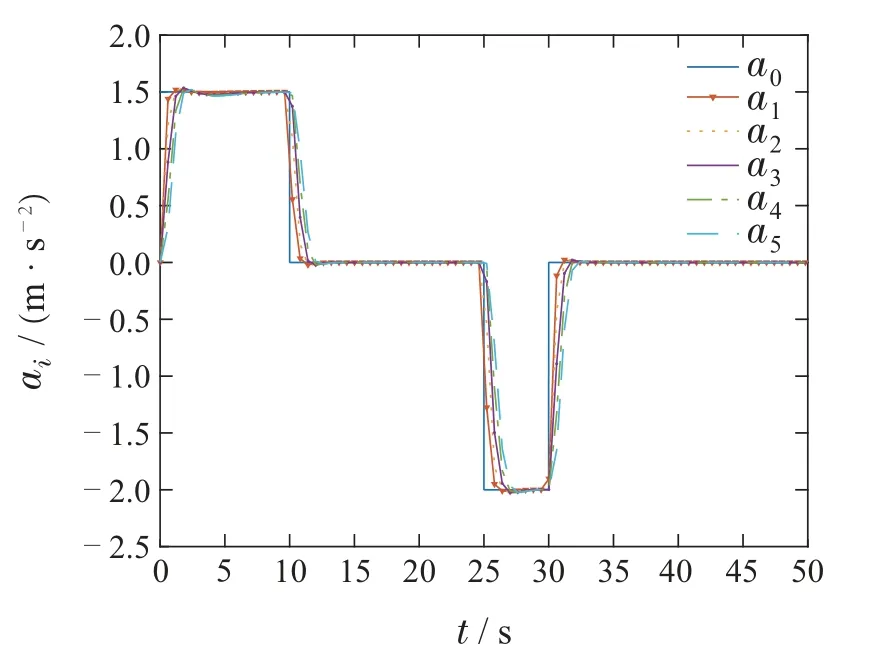
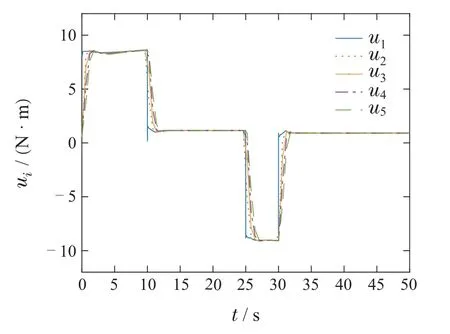
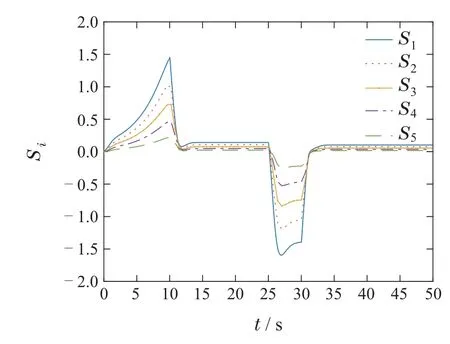
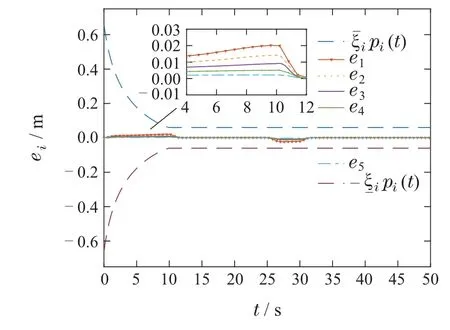
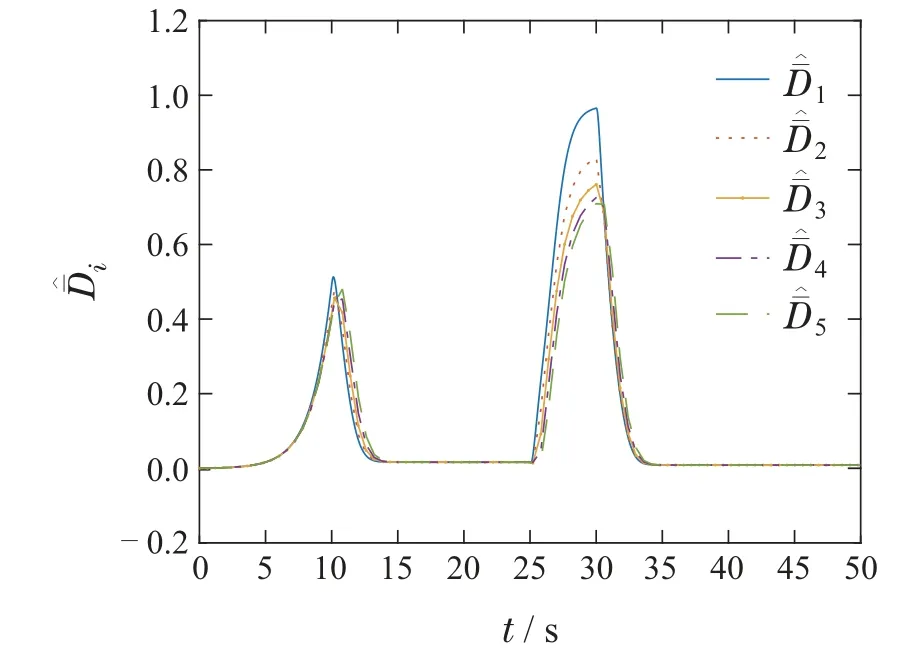
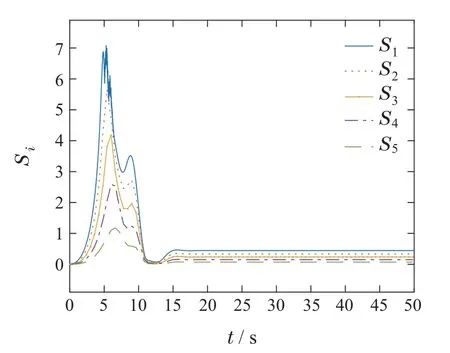
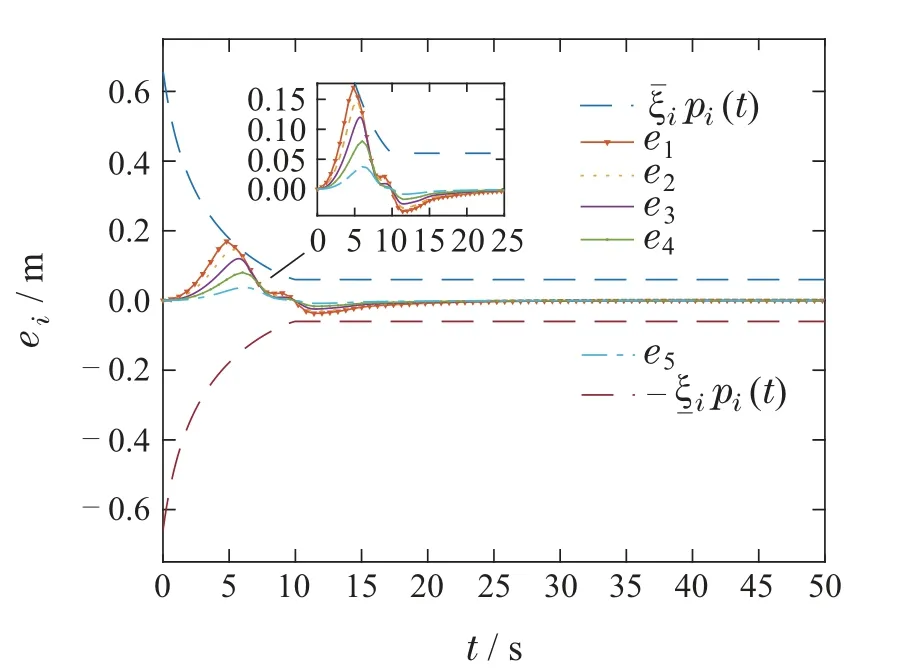
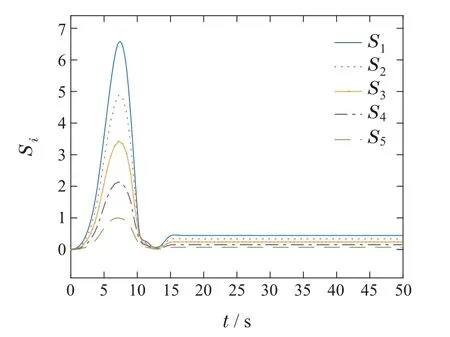
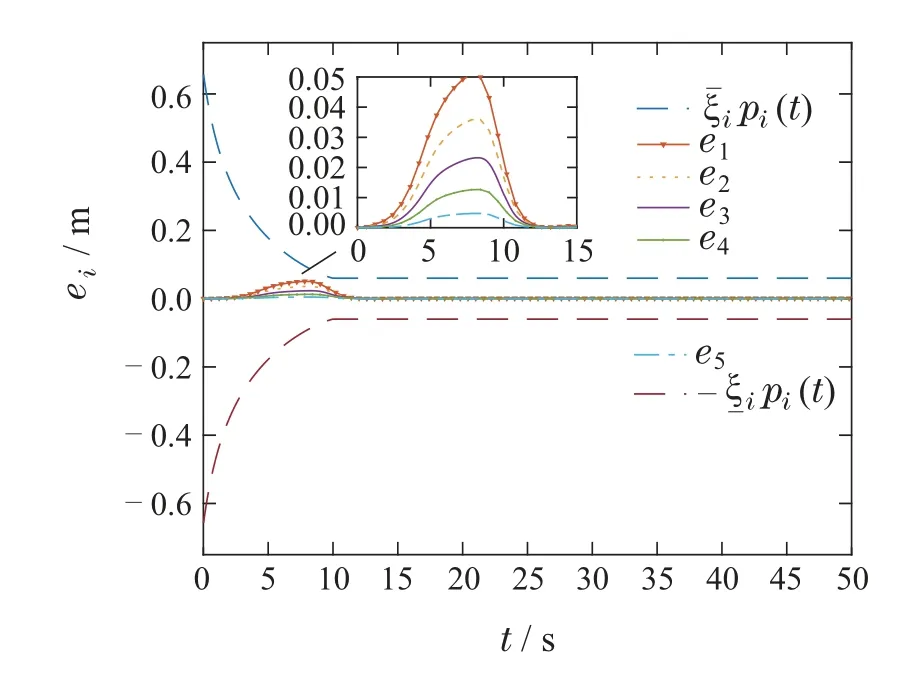
其中:α1>0,ι>0,0 对滑模面Si(t)取时间t的导数,得 为了更好地描述ei(t)和ei+1(t)之间的关系,同时确保队列稳定性,引入以下耦合滑模面: 其中q是正常数,且满足0 由式(28)可得Πi(t)和Si(t)具有相同的收敛性,为后续控制器的设计,Πi(t)的导数如下: 定理1在假设1条件下,考虑车辆运动学及动力学模型为(2)–(5)的队列控制系统,给定的控制理论,包括: 恒时距间距策略(7)、误差转换(22)、改进的滑模面(25)、控制器(30)及自适应律(31),可以保证间距跟踪误差在有限时间内收敛至稳态值,即有限时间单车稳定性.此外,当0 证整个证明分为有限时间单车稳定性及队列稳定性. 有限时间单车稳定性: 该部分分两步进行证明. 步骤1Πi的有界性. 为证明Πi的收敛性,选择如下李雅普诺夫函数: 综合式(2)(29)–(30)得Πi(t)的时间导数为 将式(36)–(37)代入式(34)得 通过计算有 根据假设1,有 根据Young’s不等式得 将式(39)–(43)代入式(38)得 根据引理3,进一步可得 根据引理1可得,整个车辆队列系统是实际有限时间稳定的,即ViΠ在有限时间TiΠ内收敛到稳定区域Ωi.这里,Ωi,TiΠ满足 其中0<θi<1. 根据式(33)(47),可得Πi,Di在有限时间TiΠ内收敛于下列范围: 步骤2Ei的收敛性. 当Πi收敛到零附近较小邻域内,可近似看成Πi ≈0.由于Πi与Si具有相同的收敛特性,当t≥TiΠ时,滑模面(25)可以写成如下形式: 为证明Ei的稳定性,定义如下李雅普诺夫函数: 对其进行求导得 根据式(26)中|Ei|与ι的关系,分情况讨论. 1)当|Ei|≥ι时,有 将式(54)代入式(53)得 根据引理2 可知,当|Ei|≥ι时,Ei是全局有限时间收敛的. 2)当|Ei|<ι时,有 综上所述,Ei是有限时间收敛的,且稳定时间Ti满足Ti≤TiΠ+TiE.由于Ei与跟踪误差ei具有等价性,所以跟踪误差ei也是有限时间收敛的,即有限时间单车稳定性. 队列稳定性.通过选择合适的设计参数可使得Πi(t)收敛到零点附近的小邻域.根据式(28)可以得到 1)当|Ei|<ι时,分两种情况分析: 情况1Ei+1(t) 根据式(59)得 2)当|Ei|≥ι时. |G(s)|≤1的证明与|Ei|<ι时的证明相似,故此处省略. 综上所述,当0 定理2如果跟踪误差Ei(t)是稳定的,则预设跟踪性能(12)是可达的. 证根据有限时间单车稳定性可得,转换后的跟踪误差Ei(t)是有限时间收敛的,即Ei(t)是有界的.这里,用表示Ei的上界. 由式(22)可以推导出 根据式(64),可得 因此,当Ei稳定时,预设跟踪性能(12)是能够得到保证的.证毕. 为验证所提控制算法的有效性,在MATLAB环境中,搭建了由6辆车构成的车队仿真实验. 在仿真中,仿真参数设置如下[15]: 最小安全车间距∆i=7 m,第i辆车的车长Li=2 m,恒定时距hi=0.2 s,发动机时间常数τi=0.2,第i辆车的横截面积Ai=2.2 m2,空气质量比ρa=0.2,空气阻力系数Cai=0.35,每辆车的质量mi=1600 kg,重力加速度g=9.8 m/s2,道路坡度θi=0,道路滚动阻力系数bi=0.02,外部扰动ωi(t)=0.1 tanht,模型不确定性∆fi(vi,ai)=0.5fi0(vi,ai),领队车初始位置和速度分别为x0(0)=45 m,v0(0)=0 m/s.跟随车的初始位置和速度为xi(0)=[36.2 27.5 17.8 9.2 0]m,vi(0)=0 m/s,i=1,2,···,N. 根据ρi(t)可得:ρi(0)=1.1,λi=1,ρi(Tf)=0.1,有限时间Tf=10. 为了更好地验证本文算法的有效性,选取如下两种不同的加速度类型: 类型1、类型2. 4.2.1 类型1 领航车加速度设置如下: 仿真结果如图3–9 所示.图3 为车辆的轨迹信息,可以看出,跟随车可以在有限时间内跟踪领队车,保持队列行驶且无碰撞.图4–5分别为各车辆速度和加速度信息,每辆车的速度都在平稳地增加,并且在t=12 s各车辆速度及加速度达到一致.图6为跟随车控制输入,当队列稳定之后,控制器的输出值也保持不变.图7为滑模面信息,滑模面可以在有限时间内达到稳定状态.图8为队列中各车辆跟踪误差,可以看出,跟踪误差的最大超调始终保持在规定的界限之内并且收敛速度也得到了提高,即跟踪误差可以在有限时间内快速收敛至规定范围之内,每辆车最终都能以期望的车间距平稳运行.此外,队列稳定性也得到保证,即|e5(t)|<|e4(t)|<|e3(t)|<|e2(t)|<|e1(t)|.图9为自适应律,可以看出本文所设计的自适应律的估计是有界的. 图3 队列中各车辆的位置信息xi(t)Fig.3 The position xi(t)of each vehicle in the platoon 图4 队列中各车辆的速度信息vi(t)Fig.4 The velocity vi(t)of each vehicle in the platoon 图5 队列中各车辆的加速度信息ai(t)Fig.5 The acceleration ai(t)of each vehicle in the platoon 图6 队列中各车辆的控制输入信息ui(t)Fig.6 The control input ui(t)of each vehicle in the platoon 图7 滑模面Si(t)Fig.7 The sliding mode surface Si(t) 图8 队列中各车辆的跟踪误差ei(t)Fig.8 The tracking error ei(t)of each vehicle in the platoon 图9 自适应律Fig.9 The adaptive law 4.2.2 类型2 领航车加速度设置如下: 参数取值与第4.1.1 节类型1 相同,仿真结果如图10–16所示. 图10 队列中各车辆的位置信息xi(t)Fig.10 The position xi(t)of each vehicle in the platoon 从图10–16中可以看出,即使存在加速度突变的情况,每辆车都能保持平稳运行,不会出现碰撞的情况.此外,跟踪误差的最大超调始终能保持在规定的界限之内,并且队列稳定性依然能够得到保证.因此,该方法可以很好地实现队列的控制目标. 为了进一步凸显本文所设计的基于改进滑模的有限时间控制方案的优势,在选择与式(66)相同的性能函数前提下分别与PID滑模控制方案和传统有限时间滑模控制方案进行如下仿真比较.这里,加速度选取类型1. PID滑模面选择如下[29]: 参数选择为Kp=3,Ki=0.5,Kd=1.仿真结果如图17–18所示. 传统有限时间滑模选择为[12]:α1sigaEi,参数选择为,α1=12.仿真结果如图19–20所示. 图17–18分别为传统PID滑模控制方案的滑模面Si和跟踪误差ei,图19–20分别为传统有限时间滑模面控制方案的滑模面Si和跟踪误差ei.从上述仿真图可以看出不同算法都可以实现队列控制.进一步,结合表1,通过对比图7、图17和图19,可以看出本文设计的改进的有限时间滑模面误差更小并且收敛的更迅速;通过对比图8、图11和图13,可以得到给定的控制方法比PID滑模控制和传统的有限时间滑模控制有更小的超调,收敛速度更快且稳态误差更小,可以更好地实现车辆队列控制目标. 表1 不同控制控制方法性能比较Table 1 Comparison of different control methods 图11 队列中各车辆的速度信息vi(t)Fig.11 The velocity vi(t)of each vehicle in the platoon 图12 队列中各车辆的加速度信息ai(t)Fig.12 The acceleration ai(t)of each vehicle in the platoon 图13 队列中各车辆的控制输入信息ui(t)Fig.13 The control input ui(t)of each vehicle in the platoon 图14 滑模面Si(t)Fig.14 The sliding mode surface Si(t) 图15 队列中各车辆的跟踪误差ei(t)Fig.15 The tracking error ei(t)of each vehicle in the platoon 图16 自适应律Fig.16 The adaptive law 图17 滑模面Si(t)Fig.17 The sliding mode surface Si(t) 图18 队列中各车辆的跟踪误差ei(t)Fig.18 The tracking error ei(t)of each vehicle in the platoon 图19 滑模面Si(t)Fig.19 The sliding mode surface Si(t) 图20 队列中各车辆的跟踪误差ei(t)Fig.20 The tracking error ei(t)of each vehicle in the platoon 本文研究了具有预设性能的网联车辆队列协同控制问题,同时考虑了外界扰动及模型不确定的影响.首先,提出了一个新型的预设性能函数,使跟踪误差在期望时间内收敛至预设的稳态误差范围内,提高了系统的响应速度.然后,构建了新的基于改进滑模的队列控制器,实现了具有集总扰动的有限时间队列控制,保证了单车的稳定性、队列稳定性及预设的瞬态和稳态性能.最后,通过仿真验证了所提方法的有效性.本文给定控制算法的收敛时间依赖系统初始状态,这会大大降低该算法的适用性.未来,探寻不依赖系统初始状态的有限时间队列控制算法将是极有意义的研究课题.3.2 控制器设计
3.3 稳定性分析
4 数值仿真
4.1 仿真设置
4.2 仿真结果
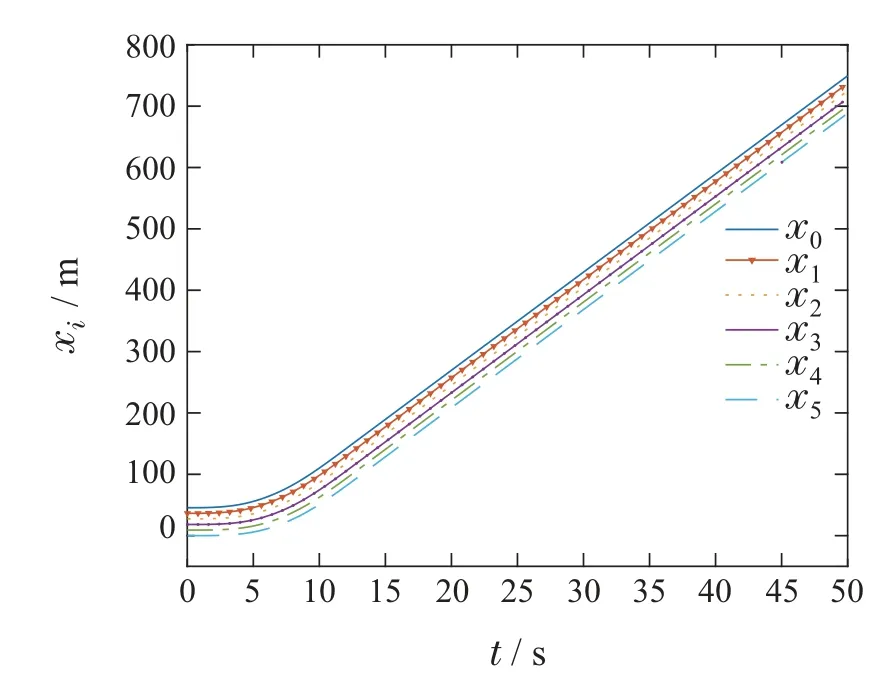
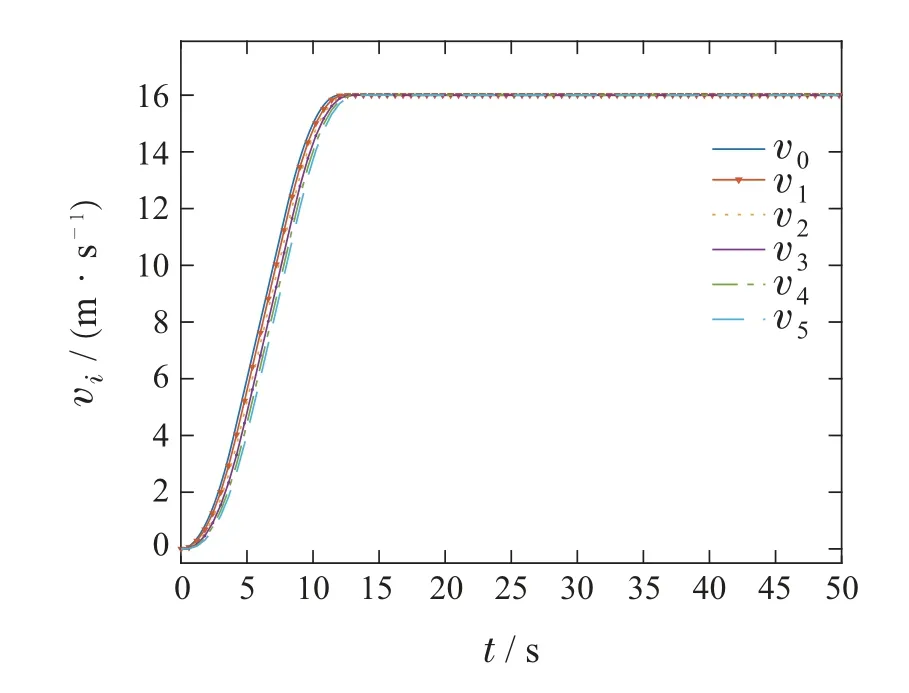
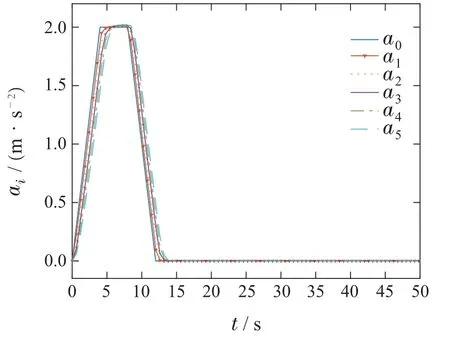

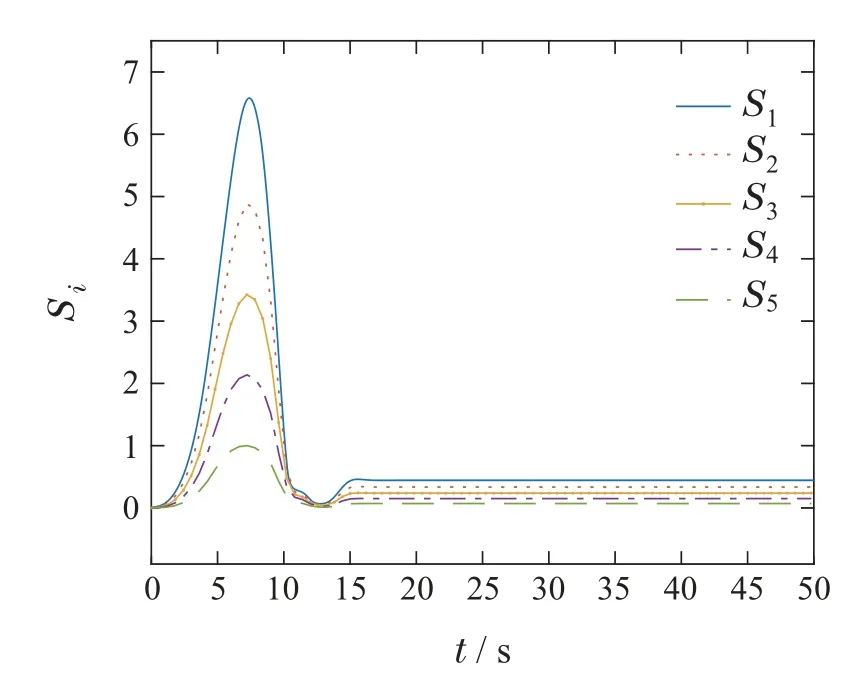
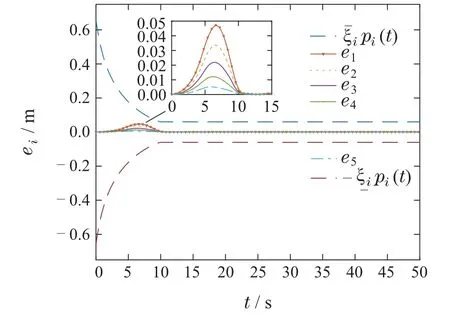

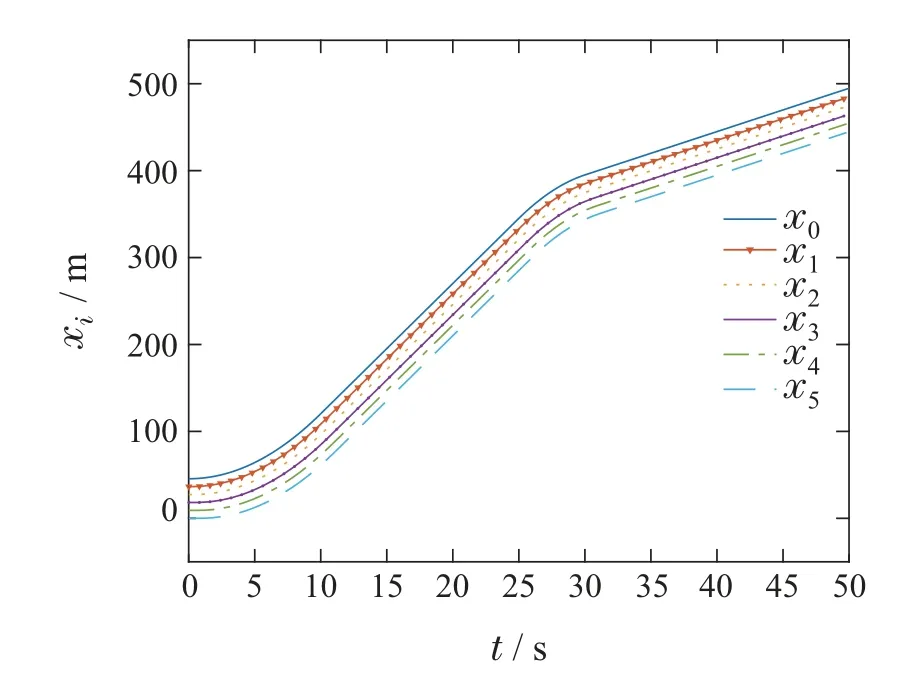
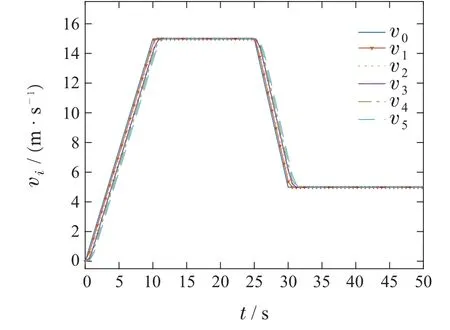
4.3 仿真对比
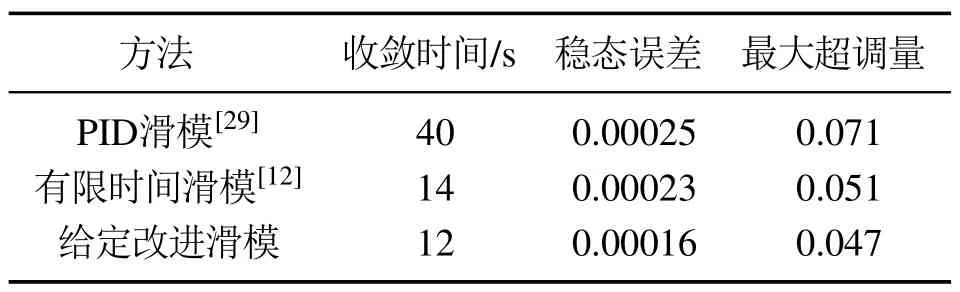
5 总结

