基于过零检测的Buck变换器自适应连续滑模控制
王艳敏 ,张伟琦†,龙 云 ,张涵清 ,冯 勇
(1.哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨 150001;2.哈尔滨工程大学动力与能源学院,黑龙江哈尔滨 150001)
1 引言
Buck变换器是一类典型的包含开关特性的非线性系统[1],大量研究已证明滑模控制(sliding mode control,SMC)以其卓越的鲁棒性和瞬态响应特性可满足不同电路拓扑及不同场合下的输出电压品质要求[2–3].然而目前仍以传统一阶SMC应用为主,抖振问题严重制约其动静态控制性能[4].特别地,如何将输出电压误差限制在给定范围是一个具有挑战性的研究问题.
从数学机理上,抖振问题的产生与SMC控制器中包含的切换非线性sgn(·)有关,表现为系统在滑模面两侧来回穿越式的高频信号振荡[4–6],会引起Buck变换器输出电压谐波化、高开关损耗、电磁干扰等诸多问题,严重降低电压输出的品质.目前抖振抑制方法主要分为3 类: 边界层法[7]、SMC 与智能化方法相结合[8–9]及高阶滑模(high-order sliding mode,HOSM)[10].边界层法的原理是将系统的运动轨迹限制在预先设计滑动模态的某一邻域内,切换控制sgn(·)被替代为饱和函数[11]或被近似为某些函数[12],以实现控制的连续性,但边界层的存在却会在一定程度上降低系统的控制精度和鲁棒性.SMC与模糊控制[9]、神经网络[8]等智能化方法相结合的做法,其原理是自适应地调整控制器增益来柔化切换控制sgn(·)的作用,但控制性能却严重依赖于人为设定的智能化判断规则.特别地,HOSM 是近年新兴的一种连续SMC 方法[13],常见算法包括Twisting算法[14]、Super-twisting算法[15]、次优算法[16]等,被视为本质解决抖振问题的一种有效方法,其控制思想是基于相对阶概念[13],通过将切换控制sgn(·)直接加到滑模变量高阶导数,使得实际控制量经过积分或低通滤波而连续化.然而,常规HOSM算法的控制增益通常设定为固定值,其取值多取决于初始阶段的暂态性能或需要克服的扰动,但随着系统轨迹趋向平衡点,固定的控制增益却成为破坏系统稳态性能的关键,过大值会带来大的稳态误差和响应时间[17–18].
为克服固定控制增益造成系统较大稳态误差的问题,变控制增益SMC控制方法应运而生[19].目前自适应机制主要有基于稳定性和基于切换时间原理的两类.对于前者,其控制增益多仅以保证系统的稳定性为前提,较少考虑诸如稳态误差等某种特定控制性能指标.例如Wang等人[20]提出一种基于观测器的二阶SMC方法,在保证系统Lyapunov稳定性的前提下,利用观测器实时输出变化的控制增益;Shtessel等人[21]以系统状态和控制增益为变量构造一种Lyapunov函数,在保证系统稳定性基础上提出一种自适应Twisting算法,使其控制增益随系统以螺旋状收敛到平衡点而不断改变.对于第2类基于切换时间原理的变控制增益SMC方法,其控制思想遵循了SMC固有的切换特性,自适应机制取决于系统趋于平衡点的运动轨迹.Corradini和Orlando[22]从系统暂态特性分析入手,将其运动轨迹用多个切换模型表征,继而提出一种多模型切换的变增益控制方法;类似地,Magni等人[19]也提出一种基于多模型切换的预测控制方法,实现变控制增益的目的.尽管相比于第1类基于稳定性的变增益原理,第2类方法更能直接建立增益变化与稳态误差等某些性能指标的影响关系,但目前研究成果较少,变增益机制与切换时刻、系统稳定性等关键问题有待深入研究.
基于以上对SMC抖振问题和变控制增益两方面的研究分析,本文以Buck变换器为控制对象,提出一种基于在线过零检测自适应机制的连续SMC方法,可保证其输出电压的稳态误差收敛到给定范围.本文创新地从滑模面和控制律两方面改进传统SMC控制方法,基于系统运动轨迹分解后的两个阶段,直接将期望的稳态误差和利用低通滤波抑制抖振的思想纳入到控制器设计中,在保证系统稳定性前提下,通过实时测量和控制过零点的个数,有效解决抖振问题,且提高输出电压品质.通过与传统一阶和二阶SMC方法的对比性理论和仿真研究证明所提方法的正确性和优越性.
2 系统描述
图1为典型的Buck变换器SMC控制系统框图,其中E为直流输入电压源,vc为输出电压瞬态值,VD为限流二极管,Sw为可控开关管,常以MOSFET和IGBT应用居多,但区别地是,可控开关管Sw的门极驱动信号用u表示,即u只能取0和1两个值,而SMC控制信号为占空比d,通过辅助脉宽调制(pulse width modulation,PWM)电路控制Sw的通断;L,C,R分别为滤波电感、电容和负载电阻,iL和iC分别为流过电感和电容的电流.
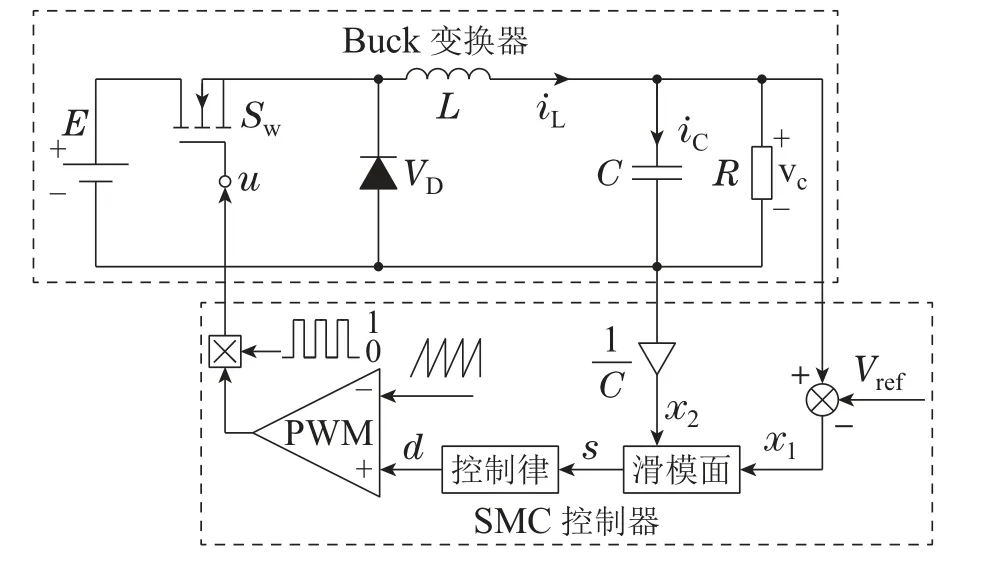
图1 Buck变换器SMC控制系统框图Fig.1 Diagram of Buck control system with SMC
针对Buck变换器,假设工作在连续电流模式(continuous conduction mode,CCM).基于基尔霍夫电路定律,其平均状态模型为[1]
定义vref为输出电压vc的给定值,系统状态x1=vcvref,x2==,则式(1)可变换为
针对SMC控制器,目前多以一阶[23]和二阶控制方法应用为主,控制器设计均包括滑模面和控制律两部分,其中滑模面多采用
其中: 设计参数c1>0;x1和x2可通过测量电压及利用霍尔传感器测量电流直接获得,由图1可知,x2=iC/C,简单且易实现.一旦Buck变换器控制系统收敛到滑模面s=0,系统的动静态性能取决于=-c1x1,即输出电压偏差x1(t)=x1(0)e-c1t以指数形式渐近收敛到零,且设计参数c1越大,系统的收敛速度就越快.
在控制律方面,一阶SMC和二阶SMC控制律的设计皆需要满足滑模到达条件s<0以保证系统稳定性.然而,从HOSM基于相对阶的抖振抑制[10,13]机理,两者的区别在于: 一阶SMC将切换控制项sgn(·)直接作用于滑模变量的一阶导数上,以保证一阶滑动模态s=0的存在[23],之后由式(3),则实现Buck变换器输出电压偏差及其导数x1=x2=0,但却会存在抖振问题;而二阶SMC,作为最简单的HOSM,则将切换控制项sgn(·)作用在滑模变量的二阶导数上,使得实际控制量对sgn(·)经过一次积分或低通滤波作用而连续化,且同时实现了二阶模态=s=0和系统状态x1=x2=0的收敛性.
下面以目前较为常用Twisting算法为例,具体阐述二阶SMC算法的抖振抑制机理,并为本文基于在线过零检测自适应机制的连续SMC方法的提出和后续的性能对比奠定基础.
3 传统固定增益二阶SMC控制
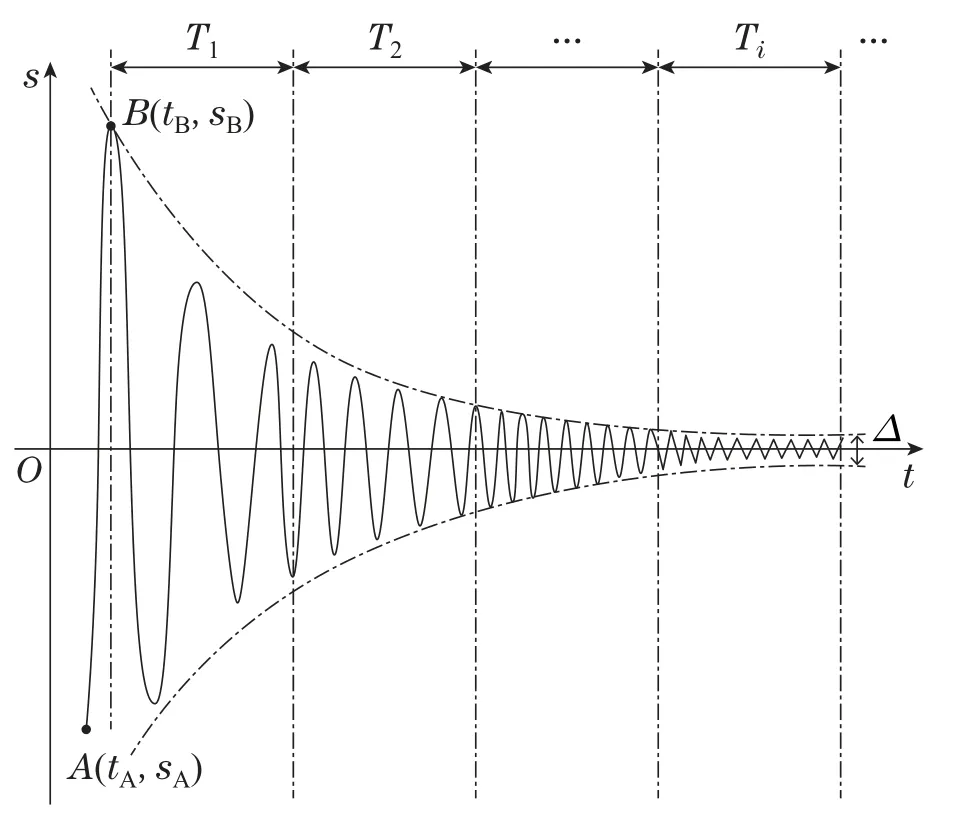
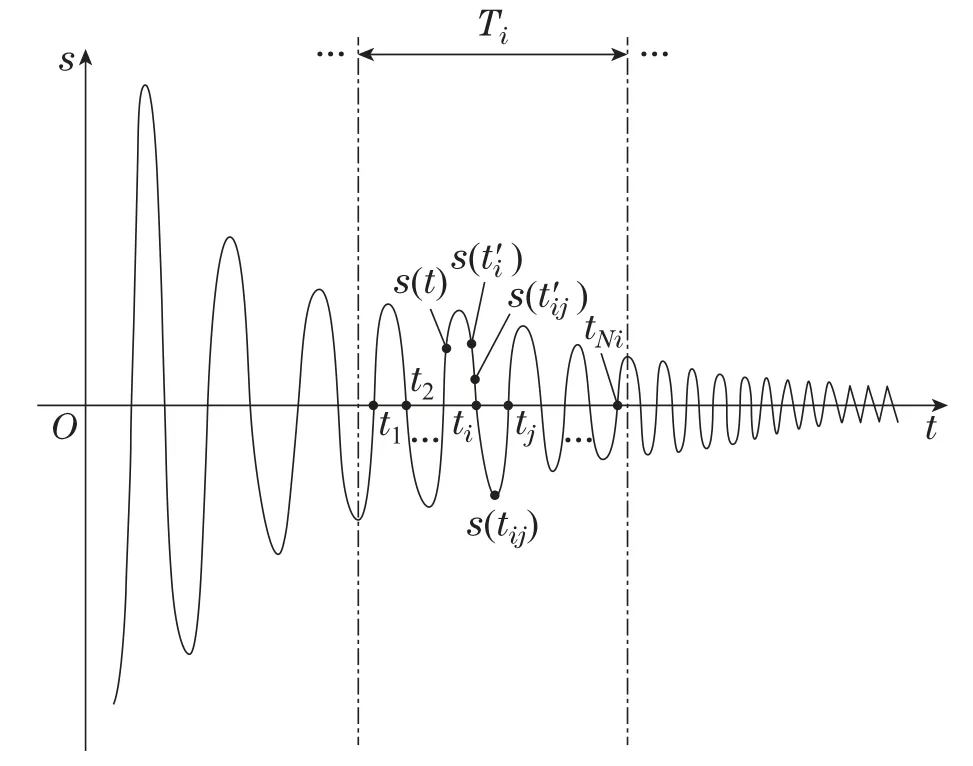
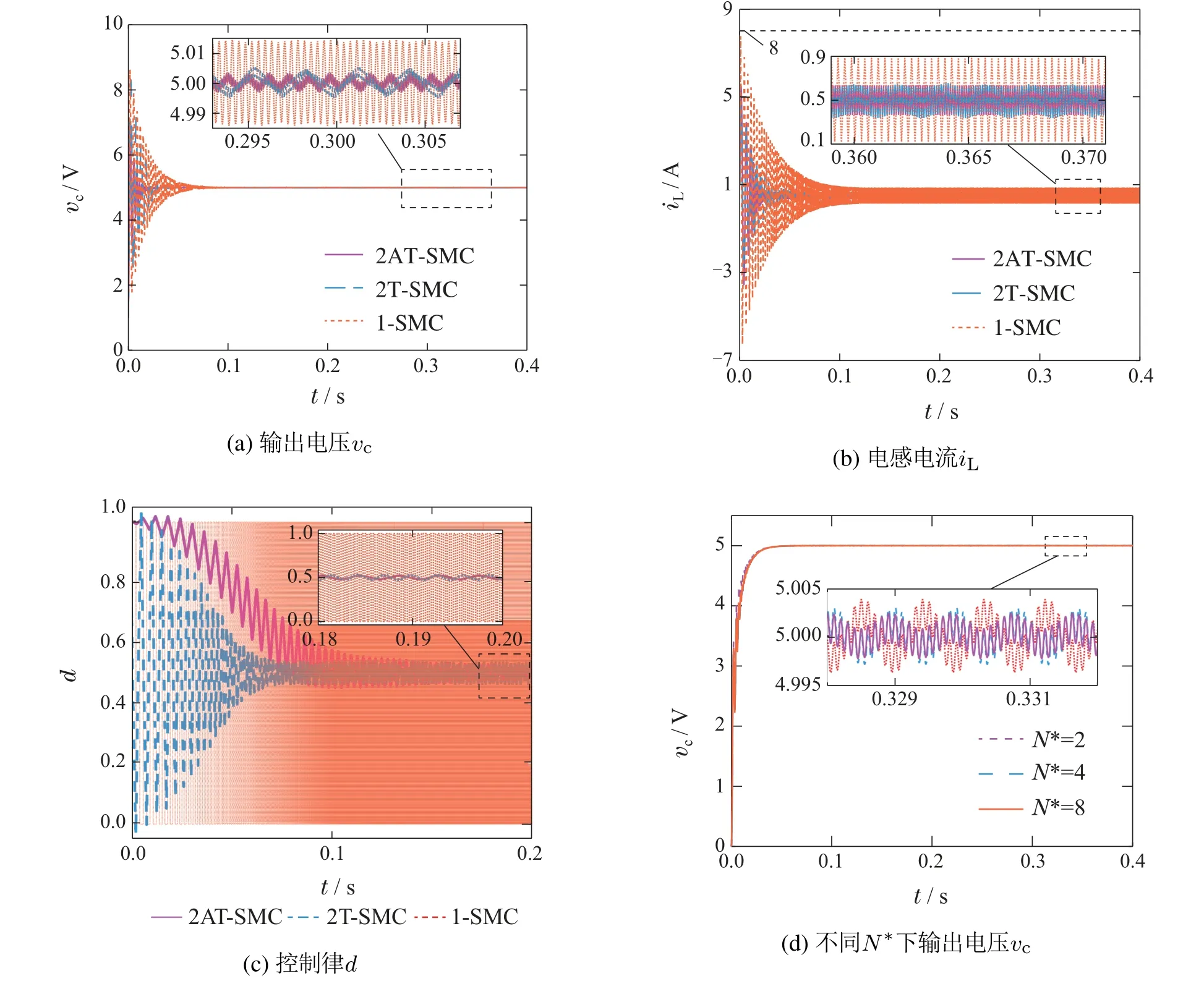
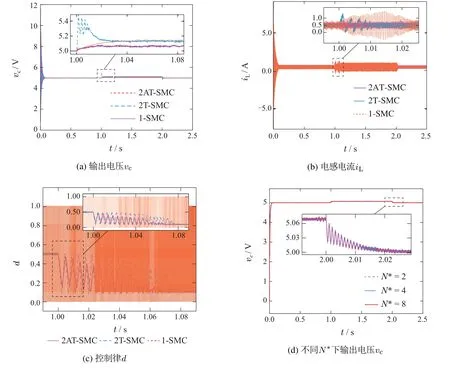
针对式(2)Buck变换器,这里进一步考虑到实际调压能力的限制,定义Emax是输入调压范围的最大值,即有0 其中: 控制增益r1>0,r2>0,且r1,r2的选择与系统的响应速度和稳态误差有关,可详细参考文献[14];由于切换控制项sgn(·)出现在控制律的一阶导数上,使得实际输出d经过积分作用而连续化,这是Twisting算法有效解决抖振问题的原因所在. 联合式(2)–(3),对滑模变量s求对时间的二阶导数,对应的切换控制项sgn(·)可直接显现出来,则有 其中:h(x1,x2,d)和µ表示为 其中: 由于直流输入电压0 定理1针对式(2)中的Buck变换器,滑模面和控制律分别设计如式(3)–(4),如果控制增益r1和r2满足如下关系,则可保证系统稳定: 证由式(5)–(8),可推出如下关系式: 根据HOSM的稳定性条件[10,13],如果Twisting算法控制下的Buck变换器系统稳定,需要判断式(10)二阶滑模的符号情况.正如其名,若系统能保持稳定,则式(3)滑模变量s将在相平面s-内以螺旋形状收敛到原点,如图2所示. 图2 基于Twisting算法的Buck变换器收敛轨迹Fig.2 Convergence trajectory of Buck converter with twisting algorithm 图2中,根据变量s和在I,II,III和IV4个象限的不同符号,式(4)控制律具有不同的数值;{Sij|i=1,2,3,··· ;j=1,2,3,···}表示运动轨迹与两坐标轴的交点,按照从外往里的方向5,第1圈轨迹半径最大,且应有|Sij|>|Si+1j|,|Sij|>|Sij+1|以保证第i+1圈轨迹半径总小于第i圈.基于以上Twisting控制系统轨迹的特点,下面以S12→S22第1圈顺时针运动轨迹为例,分左半平面和右半平面两种情况分析二阶滑模的符号情况,继而推导出系统的稳定性条件. 1)当系统处于左半平面,沿着S12→S14运动时,值从负值连续变化到正值,因此>0,但其递增速率却不同,这归因于第III象限内控制律=r1+r2,而第IV象限内控制律=r1-r2>0.联合式(5)–(8),为保证系统稳定性,则需式(10)满足关系式(9). 2)当系统处于右半平面,沿着S14→S22的运动与左半轴S12→S14的运动类似,但因为式(4)控制律在I和III象限,II和IV象限互为对称,数值却互为相反数,因此值从正值连续变化到负值,即<0,且其递减速率在第I象限会大于第IV象限.类似于式(9),保持系统在右半平面稳定的关系式应满足 其与式(9)形式是一样的. 可见,综合图2和系统在左右半平面两种情况下的稳定性分析,当控制增益r1和r2满足式(9)可保证整个系统的稳定性.证毕. 注1传统二阶SMC控制方法多采用固定的控制增益.本文以传统Twisting算法为例,由式(4)和图2,可见控制增益r1和r2在系统以螺旋状收敛到原点的整个过程保持不变.然而,越靠近原点,过大的控制增益会破坏系统的稳态性能. 为解决传统二阶SMC固定增益的问题,本文以Twisting算法为例,提出一种基于在线过零检测自适应机制的连续SMC方法,从滑模面和控制律两方面改进传统方法,以提高Buck变换器的控制性能. 为提高Buck变换器的稳态性能,不同于式(3)的传统滑模面,这里有目的地引入系统状态的积分项,即 其中 类似式(5),这里进一步求滑模变量s对时间的二阶导数,则切换控制项sgn(·)显现出来,即由式(13)可推得 其中:y21(w,s)和y22(w,µ)可表示为 为后续阐述方便,由式(16)–(17),定义4个常量ζ1,ζ2,ζ3,ζ4和函数Y21,Y22分别为 满足下面关系式: 在控制律d的设计上,本文基于切换时间原理[19,22],按照一般控制系统的收敛过程,如图3所示. 图3 控制系统的收敛过程Fig.3 Convergence progress of control systems 图3中,将其运动轨迹分成两阶段,即第1个阶段是从初始点A到达首次波峰位置点B,第2个阶段是B点之后,被分割成等时间间隔T的采样周期,表示为T1,T2,···,Ti.特别地,这里将期望的稳态误差∆纳入到式(4)传统Twisting控制律的改进中,将两个阶段的控制律d分解为d1和d2两部分,设计过程如下. 1)阶段1: 点A到点B的运动. 在图3中,假设初始点A的时刻为tA,对应的位置为(tA,sA),首次波峰位置点B的时刻为tB,对应的位置为(tB,sB),且有(tB)=0.对比式(4),这里将此阶段的控制律d1设计为 其中:k>0为常数;µmax与µmin分别是式(7)定义的µ的最大与最小值. 定理2针对式(2)Buck变换器,如果滑模面设计如式(13),阶段1的控制律设计如式(21)–(22),则系统有限时间达到B点. 证首先证明图3中B点的存在性,因为它为首次波峰位置点,满足(tB)=0.为此,将式(21)代入式(15),并联合式(19),则有 进一步,可以得到 因为sgns≤-k≤0,两边同乘|s|,即有s≤-k|s|成立,进而说明从任意初始点A,可在有限时间t0(t0=tB-tA)内到达B点.证毕. 2) 阶段2: 点B后的收敛运动. 图3中,当t>tB后,系统进入第2阶段收敛运动,可见,振幅不断减少,最终以稳态误差∆在s=0处等幅振荡.创新地,这里将期望的稳态误差∆纳入到该阶段控制律的设计中.对应地,控制律d2可设计为 其中控制增益r3>0为固定值,而另一个变控制增益Uj则在Tj采样区间内通过检测s过零点而自适应变化{j=1,2,3,···},即有 其中:Nj为Tj采样区间内s的过零点个数,N∗为其参考值,N∗≥2;Λ1和Λ2是两个正数,且有Λ1≤Λ2;U0是B点控制律d2的初始值,对应阶段1中B点控制律d1最大值,由式(21)表示为 其中:d1max是d1的最大值;‖w‖∗为w上限,即有 其中q=[q1q2],且q1与q2均为正数. 定理3对于式(2)Buck变换器,如果改进的 滑模面设计如式(12),阶段2的变增益控制律设计如式(25)–(26),则可保证系统收敛于范围 证当Buck变换器控制系统处于阶段2时,将式(25)–(26)变增益控制律代入式(15),则有 由图3,因为B点为第1阶段首次波峰位置,也是第2阶段振荡幅值最大的点.因此,联合式(7)(21)–(22)和式(27)–(28),则式(30)可进一步变为 这里以Tj采样区间为例,给出单个采样周期T内系统过零点的分析情况,如图4所示. 图4 单个采样周期T内的系统过零点情况Fig.4 Zero-crossing points in a sampling time T 假设i∈[1,Nj],j∈[1,Nj],且i 其中t是Tj采样区间的任意时刻,且|t-tij| 因为|t-ti| 对式(34)两端同时求积分,即可推导出式(29)系统的收敛范围.证毕. 注2在图3阶段2运动过程中,随着系统趋向平衡点,s的振幅会变小,在同样采样周期内的过零点个数会增多.由式(28)可知,Nj与N∗的大小关系会影响下一个采样周期Tj+1的控制增益Uj+1,因此给定值N∗的选取至关重要.在实际系统,N∗可通过实验方式测量,可取N∗=max{2Tfj+1},j∈[1,Nj],其中fj=Nj/T是实验测得s过零点的频率.由该式选取得到一个较大的N∗值,可在式(26)中不断微增控制律增益,以加快系统的收敛速度;而当系统完全进入稳态之后,此时系统状态过零频率较高,通过式(26)中的比较会反向微减控制增益,以避免不必要的过大增益造成的系统抖振问题. 注3联合图3和式(26),本文在研究系统收敛运动和设计控制律时将系统输出的期望稳态误差∆考虑在内.首先由式(29)中的系统收敛范围,可初步确定∆的最大边界,再通过进一步调整式(26)中系统控制律幅值参数N∗以达到间接控制系统稳态性能的目的.且为了保证式(26)中的收敛范围,采样周期T应当满足以下条件: 其中:sB是图3中系统状态首次达到峰值时对应的幅值;U0,r3,Uj分别是式(25)–(27)中的控制律增益;q是式(28)中的常数向量.在实际应用中以具体性能为准,可调整q中参数q1与q2来调节采样区间T的宽度,即T的选择不唯一,进而可配合参考过零点个数N∗以更准确地调整系统输出精度. 注4本文应用的过零检测是一种自适应控制的设计思想,与Buck变换器采取何种模型无必然联系,亦可扩展到其他非线性模型. 针对图1Buck变换器,其电路参数如表1所示.为验证本文所提基于在线过零检测自适应机制的连续SMC方法在抖振抑制、响应速度和控制精度方面的优越性,与文献[23]为代表的一阶SMC和传统Twisting算法为代表的二阶SMC方法进行性能对比.为方便说明,分别用1-SMC,2T-SMC和2AT-SMC代表. 表1 Buck变换器的电路参数Table 1 Circuit parameters of Buck converter 针对式(2)中所示的Buck变换器,为更加统一地对控制器进行性能对比,对文献[23]中描述的1-SMC和传统的2T-SMC的滑模面均采用式(3)形式,设计参数c1选取为100,且前者控制律设计为u=0.5[sgns-1],因实际系统多采用滞环调制[24]以缓解抖振问题,如图1中所示,本文这里取滞环宽度为0.01;后者式(4)控制增益r1取240,r2取120;对于本文提出的2AT-SM C方法,式(12)滑模面参数c1仍取100,c2取0.001,式(21)阶段1的控制增益k取75,式(25)–(26)阶段2的设计参数选取为r3=0.541,Λ1=2,Λ2=4,N∗=8,T=25µs.此外,本文在仿真时采用PWM调制将连续的控制信号d转换为Buck变换器的输入开关信号u,载波的周期为10-4s,故变换器的开关频率为10 kHz;仿真步长为10-6s,过零检测的周期为25µs. 下面以额定工况和输入电压扰动两种情况为例,对3种方法作用下的Buck变换器控制性能进行对比. 1)额定工况. 额定工况下3种方法的控制性能对比如图5和表2所示. 表2 额定工况下的电压和电流性能对比Table 2 Comparision of voltage and current in rated working case 图5 额定工况下的仿真性能对比Fig.5 Comparative simulations in rated working case 其中图5(a)为输出电压vc和图5(b)电感电流iL的仿真结果,可见,3种方法均实现两者的收敛控制,输出电压vc收敛到给定值Vref=5 V,其中1-SMC的稳态误差为最大的13.01 mV,其次2T-SMC为6.04 mV,2ATSMC稳态性能最佳,稳态误差仅为1.03 mV.对比式(3)和式(12),这归因于本文所提2AT-SMC方法将系统状态的积分项引入到滑模面的设计中.同时2AT-SMC控制下的系统收敛速度也是最快的,仅为0.042 s,联合图5(c)控制律d的对比,这归因于所提2AT-SMC 方法的变增益控制作用.进一步由图3、式(21)和定理2,可见系统在阶段1的启始运动轨迹振荡最大,这也解释了此阶段2AT-SMC控制律d幅值最大的原因;之后在阶段2随着系统趋向收敛,其幅值却是3种方法中最小的.特别地,1-SMC的控制律d存在明显的抖振现象,即使采用了滞环调[24]来缓解,仍然没有2T-SMC和2AT-SMC这样的二阶SMC抖振抑制性能好.进一步,在图5(d)中,选取2,4,8 这3 个不同过零点给定值N∗,其对应的输出电压稳态误差分别为4.02 mV,3.10 mV和1.03 mV.根据N∗=max{2Tfj+1}的选取公式,可知N∗越大,过零点检测的频率越快,所提2AT-SMC方法的变增益控制性能越好,进而也证明了在线过零点自适应机制对系统性能的影响. 2)扰动工况. 这里以输入电压E的扰动为例,假设在t=1 s时由10 V跳变到12 V,后在t=2 s时又跳回到10 V,仿真对比如图6和表3. 表3 扰动工况下的电压和电流性能对比Table 3 Comparative simulations in disturbing case 图6 扰动工况下的仿真性能对比Fig.6 Comparative simulations in rated working case 对比图5 额定和图6 扰动两种情况,可见3 种方法对Buck变换器输出电压vc、电感电流iL和控制律d的影响作用是一致的,这归因于SMC 鲁棒控制的优越性.具体地,以t=1 s 输出电压vc扰动为例进行分析,可见本文所提2AT-SMC的响应速度最快,大约在1.015 s恢复到平衡状态,2T-SMC和1-SMC方法的收敛时间分别为1.038 s和1.042 s,且前者启始阶段出现震荡,这归因于传统二阶SMC方法选取固定增益使然,从图5(c)控制律d的对比也能说明其振荡的原因,即在t=1 s 扰动发生时,2T-SMC和2AT-SMC两种二阶SMC的控制律d大小接近,但本文所提2AT-SMC 方法的控制增益能随收敛过程自适应地减小,但传统固定增益的2T-SMC却始终维持较大值,进而使得输出电压vc在快速收敛过程中产生振荡.而图5(d)中同样给出不同过零点给定值N∗所对应的系统输出电压性能,易见随着N∗的增大,vc的稳态误差逐渐变小、克服扰动后的收敛时间逐渐缩短,进一步证明了N∗的选取对过零检测自适应机制下系统输出性能的关键作用. 基于以上Buck变换器在额定和扰动两种工况下的性能对比,均说明本文所提基于在线过零检测自适应机制的2AT-SMC在抖振抑制、响应速度和控制精度方面的优越性,提高了变换器的输出电压品质. 本文以传统Twisting算法为例,引入在线过零检测自适应机制,通过滑模面和控制律两方面进行算法改进,提高Buck变换器的输出电压品质.创新地,将系统状态的积分项引入到滑模面设计中,将期望的稳态误差纳入到滑模控制律的设计中,沿着系统收敛轨迹的两个阶段,分阶段推导出其变增益的连续控制律,并给出相应的稳定性分析.特别地,过零点的实时检测在实际系统简单易实现,使得所提方法具有重要的理论和实用价值.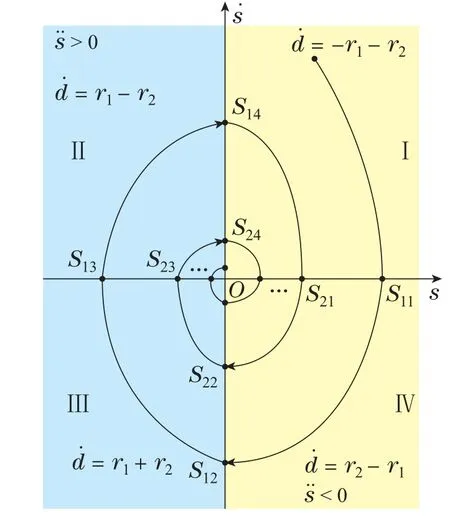
4 改进的自适应二阶SMC控制
4.1 滑模面设计
4.2 控制律设计
5 数值仿真



6 结论

