自适应比例–积分H2滑模观测器设计

王心怡 ,许 璟†,牛玉刚 ,贾廷纲

(1.华东理工大学能源化工过程智能制造教育部重点实验室,上海 200237;2.上海电气自动化集团,上海 200070)

1 引言

针对确定系统,基于状态空间模型的龙伯格观测器能有效估计被控对象的实际状态.文献[1–2]提出了龙伯格观测器的构建方法,基于当前输出的静态反馈实时矫正,实现了系统状态估计.但是,龙伯格观测器对未知外部扰动的灵敏度高.实际工程中参数不确定性和外界干扰会降低龙伯格观测器的观测精度.为了提高不确定性下系统的估计精度,国内外研究学者提出了自适应控制.基于自适应算法学习系统模型的不确定项,是处理参数不确定性和扰动的有效方法[3].径向基神经网络(radial basis function neural network,RBFNN)因其对任意复杂非线性函数的自适应学习能力而被广泛应用于自适应控制系统中[4].将神经网络和自适应控制技术结合,具有容错性好、抗干扰能力强和自学习能力强等优点.文献[5]针对一类具有未建模动态非线性非严格反馈结构的系统,提出了基于RBFNN的自适应控制方法.文献[6]针对机器人轨迹跟踪控制中由于模型参数不确定以及外部扰动引起的系统不稳定问题,提出了基于神经网络的机器人自适应控制策略,抑制了不确定性因素对控制系统造成的影响.

作为非线性鲁棒控制方法的重要分支,滑模观测因其对扰动和参数不确定性的强鲁棒性,以及对未知输入的估计能力而被广泛应用于状态重构与估计领域.文献[7–8]利用一阶滑模观测器对传感器和执行器故障进行重构,该设计方法具有快速响应、物理实现简单等优点,但在实际应用中,因需要通过较大的切换增益来消除外部干扰和不确定项,导致滑模观测器具有严重的抖振问题.此外,抖振的存在极易降低系统的稳定性,还会严重影响滑模观测器的估计精度.

为了有效抑制抖振,国内外研究学者提出了许多不同的解决方法,如饱和函数法、设计边界层法和动态滑模法等.文献[9]针对滑模控制的非线性部分提出了饱和函数法,将滑模控制中的切换函数替换成饱和函数.在边界层外采用正常的滑模控制形式,在边界层内采用线性化反馈控制.文献[10]提出了高阶滑模控制器设计方法,针对控制系统不连续导致抖振的问题,对系统方程进行多次微分,采用连续控制律取代传统的基于符号函数的一阶滑模控制律.上述方法均能有效削弱抖振,但难以兼顾系统的稳态性能.

为了在削弱抖振的同时保证观测器的稳态性能,国内外研究学者设计了比例–积分观测器(proportional integral observer,PIO),将积分器引入观测器结构中以降低稳态误差[11].PIO能够对系统外部干扰和不确定项进行估计和补偿,降低系统抖振影响的同时保证了系统的稳态性能[12–14].文献[15]提出了结合滑模控制与比例–积分控制的模糊逻辑控制器.将各子系统之间的耦合、未建模动态和外界扰动视为系统的不确定性,进行分散鲁棒自适应控制.文献[16]提出了基于最小阶扰动估计的比例–积分滑模控制.减小稳态误差的同时提高了系统抗扰性并削弱了抖振.

不同于现有的研究工作,本文利用神经网络的非线性自适应逼近能力,将RBFNN嵌入比例–积分滑模观测器中,设计自适应比例–积分H2滑模观测器.因此,本文所设计滑模切换增益可以根据扰动和不确定参数特点自适应调节,减小了自适应神经网络和模型不确定性之间的逼近误差.利用基于径向基神经网络的权值自适应律,使得滑模动态在有限时间内收敛于滑模面,实现了参数不确定性和外部扰动下非线性系统的鲁棒确切估计.

与现有部分研究成果相比,本文的主要贡献在于:

1) 将RBFNN技术引入比例–积分滑模观测器中,同时利用了神经网络对不确定参数的逼近能力和积分器对干扰的补偿能力;

2) 利用比例–积分滑模控制结构,削弱了抖振对滑模观测器稳态估计性能影响,保证了观测器对系统内部不确定性项和外部扰动的鲁棒性;

3) 给出了基于H2次优控制和区域极点配置的滑模观测器参数自整定方法,基于线性二次型(linear quadratic,LQ)性能函数对跟踪误差收敛速度进行定量调节.

2 系统描述与引理

考虑以下非线性系统:

为了便于自适应比例–积分H2滑模观测器设计与分析,本文给出了以下相关假设与引理.

假设1不确定非线性系统(2)中的外界干扰输入d(t)=[d1(t)···dm(t)]T有界,且满足(t)=0.存在正常数Ddj,使得|dj(t)|≤Ddj,0≤j≤m.

下述RBFNN的逼近引理,将在论文推导中使用.

引理1[17]作为一种线性参数化神经网络,径向基函数神经网络能以任意精度逼近紧致集上的任意连续实函数F(z),z(t)∈Rn,具体表示为

其中:Ψ(z)是n×n的基函数矩阵;n为神经元节点个数;为最优权值向量;ϵ(z)=[ϵ1(z)···ϵn(z)]T为逼近误差;|ϵi(z)|≤Dϵi,i=1,···,n,Dϵi为已知的逼近误差上界.

其中:Ωθ是θF的有效估计域;Rn是系统状态的可行域;sup表示‖F(z)-Ψ(z)θF‖的最小上界;arg min表示使得sup‖F(z)-Ψ(z)θF‖达到最小值时θF的值.

注1基于一个全局的、参数无关的、状态空间的微分同胚z(t)=T(x(t)),T(x0)=0[18],可使得本文所设计的基于径向基神经网络的自适应比例–积分H2滑模观测器适用于以下非线性系统:

其中:x(t)∈Rn,u(t)∈Rν,y∈R分别是系统状态、控制输入和系统输出;qi(x(t),u(t))是已知的关于系统状态和控制输入的平滑函数:q0(x(t),0)=0,Rn×Rν→Rn,0≤i≤n.f(x(t))和h(x(t))是系统已知的平滑函数:h(x0)=0.已知Q(x(t),u(t))=diag{q1(x(t),u(t)),···,qn(x(t),u(t))}.θ(t)=[θ1(t)···θn(t)]T是可微时变的未知不确定参数向量,0≤i≤n.d(t)=[d1(t)···dm(t)]T是未知扰动,0≤j≤m.N和H是系统已知的具有适当维数的系数矩阵.

3 基于径向基神经网络的自适应比例–积分H2滑模观测器

3.1 径向基神经网络设计

针对系统的不确定动态F(z),根据引理1中的最优近似,能够采用RBFNN的一般形式(z,θFk)自适应逼近F(z),k=1,···,n.RBFNN是一种含输入层、单隐含层和输出层的三层前馈网络.具有结构简单、训练过程快速的特点[19],其结构如图1所示.

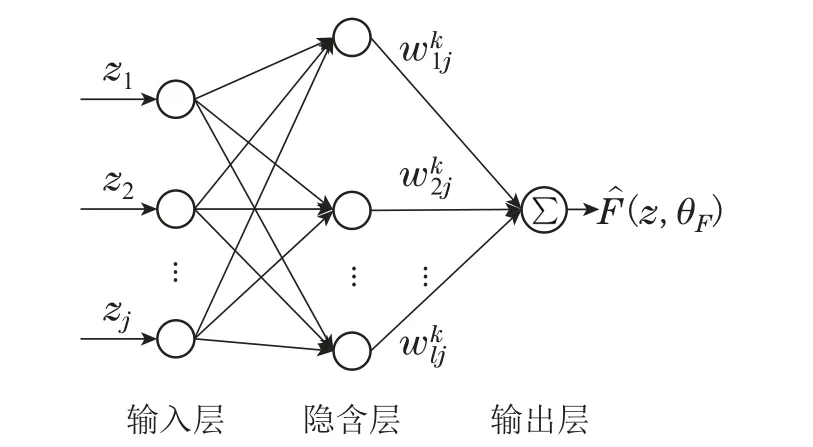
图1 径向基神经网络Fig.1 Radial basis function neural network

RBFNN输入层到隐含层的变换是非线性的,变换函数是径向基函数.它是一种局部逼近、非负非线性、对中心点径向对称衰减的函数,具有形式简单且解析性好的优点[20].与反向传播(back propagation,BP)神经网络全局逼近的待寻优参数多且收敛速度慢相比,RBFNN 局部逼近的特点使网络学习速度更快[21].

其中H(·)为隐含层激励函数.

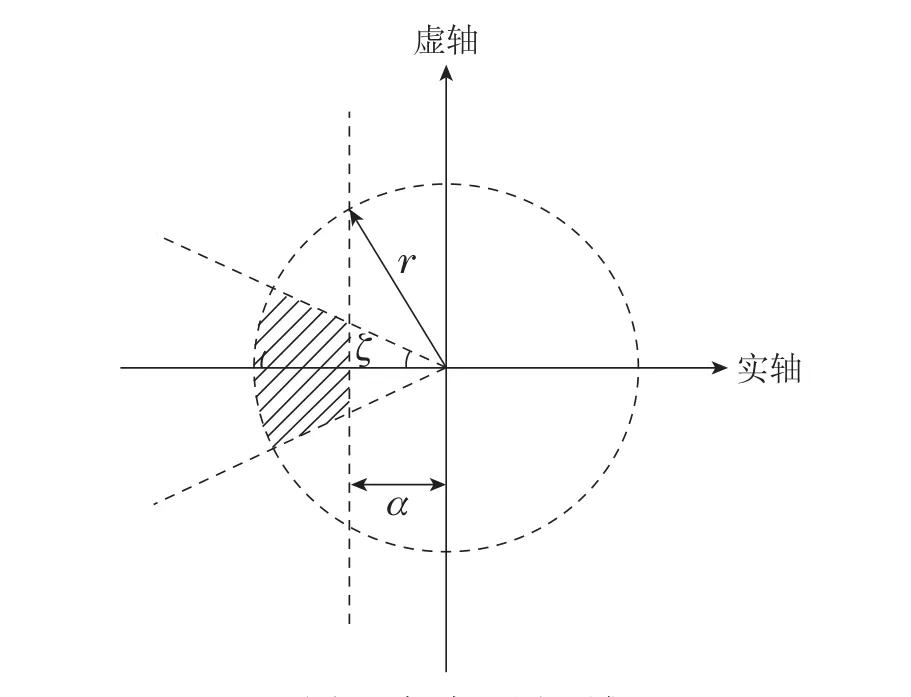
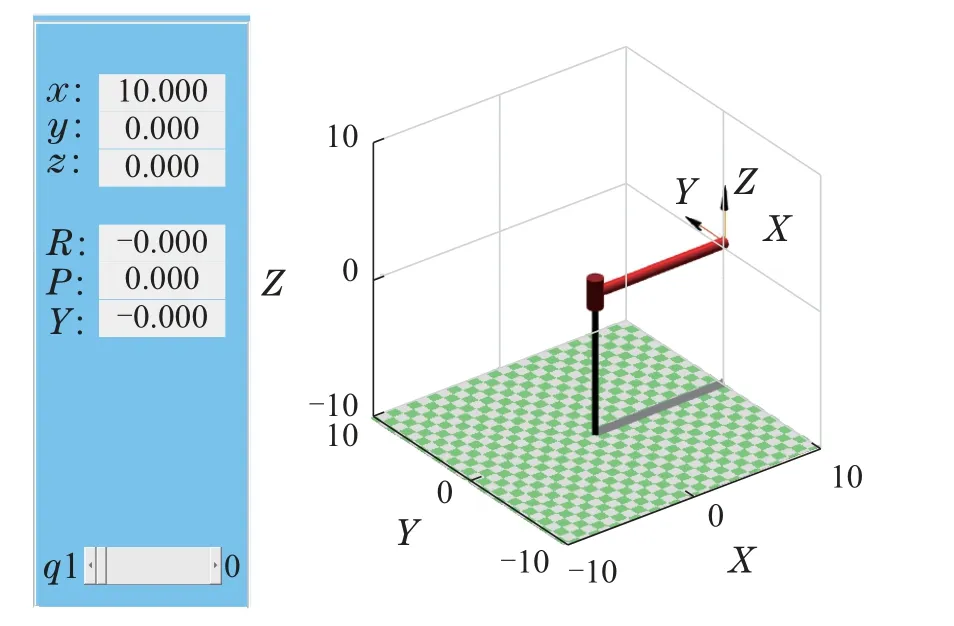
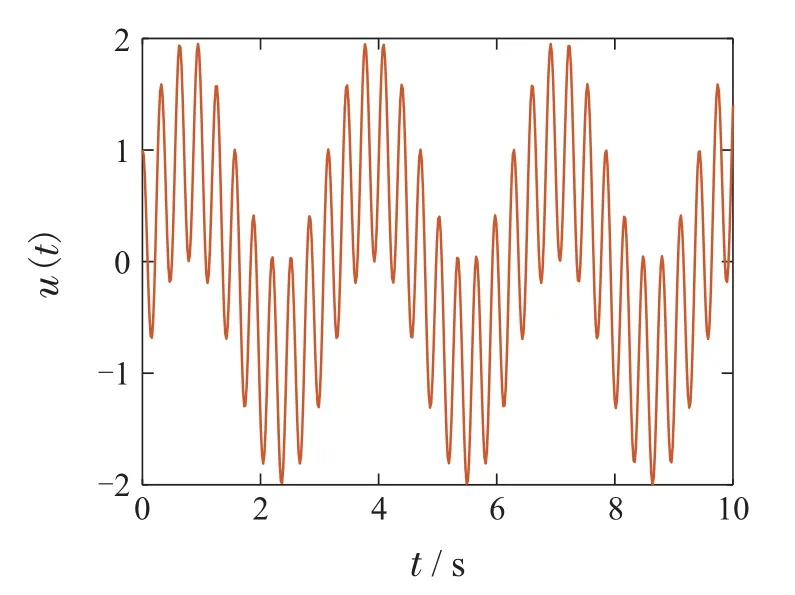
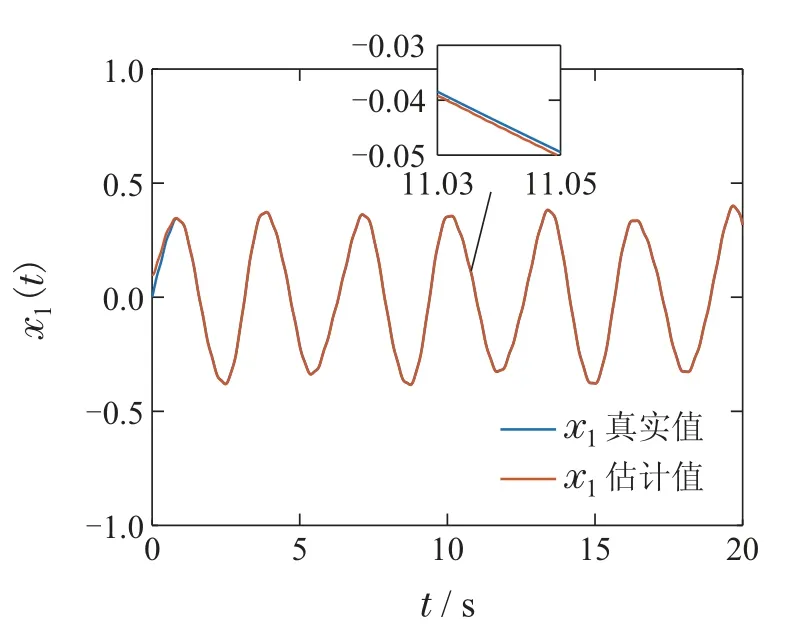
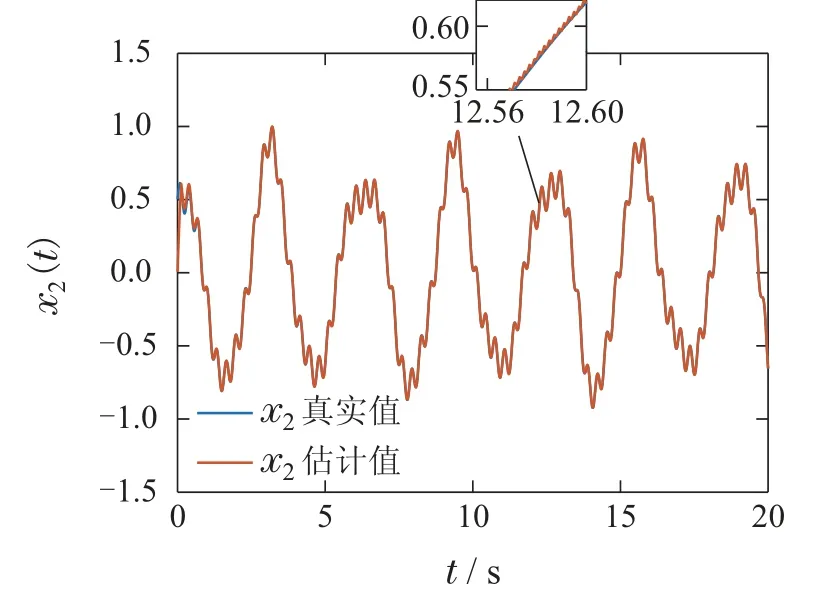
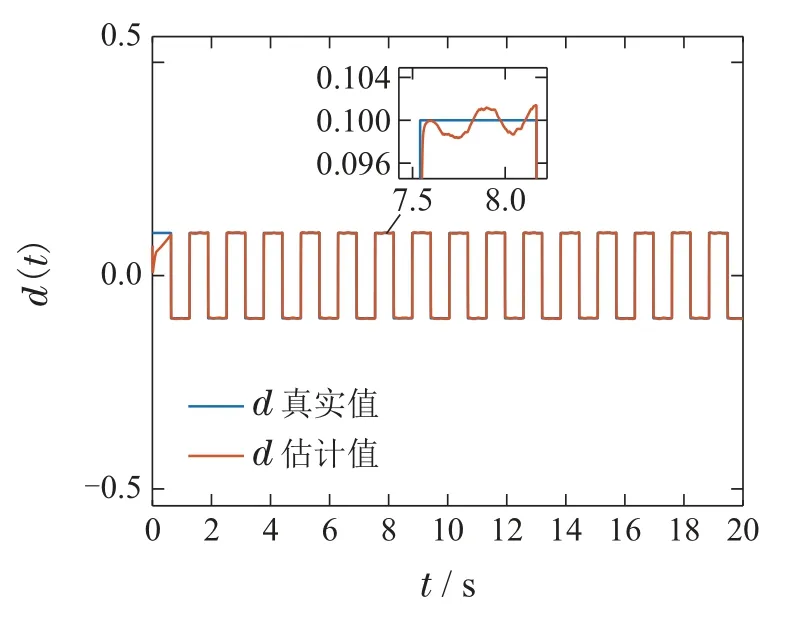
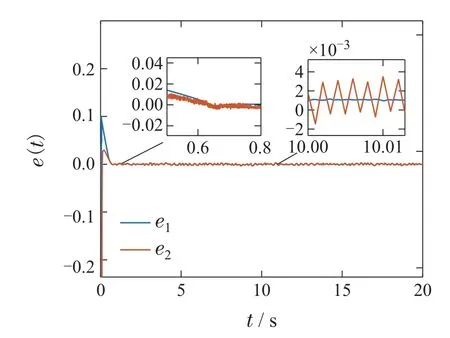
1)|H(x)-H(y)|

2)存在常数C>0,使得|H(·)|≤C,∀·∈R.

根据上述条件,选择激励函数H(·)为

注2Φ(y(t),u(t))是关于系统输出和控制输入的非线性函数矩阵,可以利用RBFNN对非线性函数的拟合能力进行有效逼近.建立基于状态误差和扰动的RBFNN自适应律,能够实现在线修正网络权值参数逼近θ(t).因此,采用RBFNN逼近F(z(t))=Φ(y(t),u(t))θ(t),可以同时解决系统中较多的非线性项,实现RBFNN权值收敛到最优值以及未知非线性系统动态的局部准确逼近.

注3选择式(8)作为激励函数的原因在于: Sinusoid(简单正弦函数)激励函数为神经网络引入了周期性,且计算简单,在正向传播和反向传播中不包含幂运算[23].同时Sinusoid激励函数的输出是关于原点对称的,保证了梯度下降的运作[24].

3.2 自适应比例–积分H2滑模观测器设计

系统状态和未知输入可以使用以下自适应比例–积分H2滑模观测器来估计:

其中:τs(t)为待设计的滑模控制律,L1为观测器的比例增益,L2为观测器的积分增益.

上述自适应比例–积分H2滑模观测器形式可以改写为

3.3 滑模控制律及自适应律设计与稳定性分析

设误差系统(16)的李雅普诺夫函数为

根据李雅普诺夫稳定理论,下述定理给出了系统(13)的自适应比例–积分H2滑模观测器稳定性条件.

则系统(14)的误差可在有限的时间内收敛到0.基于此,比例增益L1和积分增益L2可分别通过L1=P-1M和L2=P1W计算得到.

为保证系统稳定,设计神经网络权值自适应律为

将式(22)代入式(20)中的参数误差项可得

因此,式(20)可化简为

设定滑模控制律为

设计基于误差的线性滑模面

其中Bi为第i个元素为1,其余元素为零的行向量.

将Bi代入式(25)可得

通过式(27)可得

其中∆0的具体形式见式(19).证毕.

注4为解决预先设定的最优权值向量所引起的约束问题,更新自适应律如下:

综合自适应律1),2)可知,若θF(0)∈Ω0,则有θF ∈Ωθ.

4 参数自整定方法

4.1 H2次优控制

线性矩阵不等式方法(linear matrix inequality,LMI)是鲁棒控制分析与设计的重要部分,标准的LMI问题也称为广义特征值问题(generalized eigenvalue problem,GEVP),可以利用内点算法等凸优化技术进行有效地求解.

针对误差系统(16),与估计误差和控制操作相关的LQ性能指标可表述为

将式(17)和式(28)代入式(33)可得

在下式成立的条件下:

注6最优控制应由反映系统内部状态的全部信息参与组合,但本文的非线性系统具有不确定性,难以直接求解最优控制问题.采用次优控制,可在保证性能指标值足够接近最优性能值的同时,显著地减少问题求解的计算量[25].

下述定理给出了基于LQ性能指标(32)的次优控制充分条件.

定理2对于给定的标量β>0,若存在对称正定矩阵P∈Rn×n和P1∈Rm×m满足

则系统可达到H2次优跟踪性能.

最后,引入一个新的变量β>0,将式(40)中最小化问题转化为标准LMI问题[26].

因此,式(40)可转化为式(37)中的特征值问题.证毕.

4.2 区域极点配置

系统的跟踪性能与闭环极点Ae的位置有关,设计观测器增益L1和L2使得Ae位于左半平面的一个合适的子区域十分重要[27].本文将闭环极点x+jy配置在S(α,r,ζ)区域,该区域可表示为

图2中阴影部分为极点配置的目标区域S(α,r,ζ).下述定理给出了基于区域极点配置的自适应比例–积分H2滑模观测器参数自整定方法.

图2 极点配置区域Fig.2 The area of polar configuration

定理3对于给定的正标量α,r,ζ,若存在对称正定矩阵P∈Rn×n和P1∈Rm×m满足以下LMI:

则闭环极点x+jy可配置在S(α,r,ζ)区域.基于此,观测器的比例增益L1和积分增益L2可分别通过L1=P-1M和L2=P1W计算得到.

证首先,将式(42)转化成标准LMI形式

根据以上分析,具有区域极点约束的H2目标跟踪性能可以描述为以下GEVP:

5 仿真

本节采用单连杆机器人模型验证观测器的理论分析,在垂直平面上旋转的单连杆机器人运动方程为

其中:q(t)为旋转角度;I为惯性矩;u(t)为控制输入;d(t)为外部扰动;m和l分别为机器人质量和连杆长度;g为重力加速度;mglsinq(t)为不确定性项,需通过径向基神经网络进行自适应逼近.

设定单连杆机器人参数:I=0.5,m=1,l=1.则该机器人的可视化运动模型如图3所示.

图3 单连杆机器人可视化模型Fig.3 Visual model of single link robot

根据式(13)设计系统(47)的观测器方程.设定初始状态x(0)=[0 0.5]T,(0)=[0.1 0]T,(0)=0.1.控制输入u(t)=sin(2t)+cos(20t).假设扰动d(t)是幅值为±0.1,相角为的方波信号.

首先,构建径向基神经网络,设定RBFNN的隐含层神经元个数为3,其中,对于k=1,2和i=1,···,3,设定偏差分别为-4,0和4.采用常量初始化的方法进行初始权值的选取.对于k=1,2,i=1,2,3,j=1,2,将权值参数全部初始化为1.设定θF(0)=0,γ=10,κ=1,δ=0.1.

其次,选取神经网络逼近误差上界Dϵ1=0.1,Dϵ2=4.设定极点配置区域参数α=0.5,r=10,,选取模拟参数Q2=I.

基于上述参数设定和LMI 求解结果,对本文所设计的自适应比例–积分H2滑模观测器进行仿真实验,可得控制输入u(t)=sin(2t)+cos(20t)如图4所示.

图4 控制输入u(t)Fig.4 Control input u(t)

根据参数Dϵ1=0.1和参数Dϵ2=4可得滑模控制律τs1(t)=-0.1sgn(s(t))和τs2(t)=-4sgn(s(t))的曲线分别如图5–6所示.系统状态x1(t)和x2(t)的跟踪曲线分别如图7–8所示.

图5 滑模控制律τs1(t)Fig.5 Sliding-mode control τs1(t)

图6 滑模控制律τs2(t)Fig.6 Sliding-mode control τs2(t)

图7 x1(t)跟踪曲线Fig.7 Tracking curve of x1(t)

图8 x2(t)跟踪曲线Fig.8 Tracking curve of x2(t)

从图中可以看出针对具有参数不确定性和未知扰动的系统,本文所设计的自适应比例–积分H2滑模观测器能准确地跟踪对象的实际状态.

从图9中可以看出本文所设计的自适应比例–积分H2滑模观测器能够有效补偿外界干扰,提高了系统的观测精度和对扰动的鲁棒性.

图9 扰动跟踪曲线Fig.9 Trajectories of disturbance

图10中e1(t)和e2(t)分别是状态x1(t)和x2(t)的观测误差.从图中可以看出观测误差e1(t)将在0.65 s左右趋近于0,e2(t)将在0.8 s左右趋近于0.

图10 状态误差曲线Fig.10 Status error curves

6 结论

本文针对一类具有参数不确定性和有界外部扰动的单输出非线性系统,设计了自适应比例–积分H2滑模观测器.首先,通过径向基神经网络,逼近系统模型的非线性项,描述不确定性参数输入到神经网络自适应律输出的映射关系.其次,基于观测误差的线性滑模面,设计径向基神经网络权值的自适应律,使得滑模动态在有限时间内收敛于滑模面,实现了参数不确定性和外部扰动下非线性系统的鲁棒确切估计.最后,设计基于H2次优控制和区域极点配置的滑模观测器参数自整定方法.通过对单连杆机器人的仿真结果表明,该方法能够保证非线性系统具有较好的鲁棒性和自适应性.本文未来的研究工作将针对无人机系统姿态角观测,设计自适应比例–积分H2滑模观测器.