基于高阶滑模观测器的永磁同步电机无差拍预测电流控制

徐睿琦,张昆鹏,林欣魄,孔德山,刘 壮,刘健行

(1.哈尔滨工业大学航天学院,黑龙江哈尔滨 150001;2.国网黑龙江省电力有限公司伊春供电公司 黑龙江伊春 153000)

1 引言

在永磁同步电机(permanent magnet synchronous motor,PMSM)驱动系统中,传统的控制方法主要有矢量控制和直接转矩控制.但对于高速发展的工业领域而言,传统的控制策略并不能满足不断发展的工业需求,因此一些新型现代控制方法相继被学者们提出.模型预测控制(model predictive control,MPC)自问世以来已经在复杂工业过程中取得了巨大成功,从原来的启发式控制算法发展成为了工业领域新的学科分支.

目前模型预测控制方法应用在电机驱动系统中主要分为有限控制集MPC(finite control set MPC,FCSMPC)和连续控制集MPC(continuous control set MPC,CCS-MPC)两种.FSC-MPC 通过计算成本函数选择最优的电压矢量,其计算量较大.无差拍预测电流控制(deadbeat predictive current control,DPCC)是CCSMPC的一种,它可以以较小计算量,获得与FCS-MPC相似的动态和静态跟踪性能[1],因此被越来越多的研究人员关注.

DPCC作为一种典型的基于模型的方法,系统模型的失配会严重降低控制器的性能.鉴于此,国内外学者提出了很多提高DPCC参数鲁棒性方案.所提出的方案大致分为如下4种: 第1种是基于参数辨识,该方法通过在线辨识电机参数如电阻、电感、磁链等,实时更新模型参数,来消除参数摄动带来的影响.但是由于电机数学模型的欠秩性[2],同时进行辨识所有参数会导致误收敛的情况,所以一般选择个别参数主要参数进行辨识,且算法较为复杂.文献[2]在传统DPCC方法的基础上,开发了一种新的定子电阻和电感参数辨识方法,与传统的递推最小二乘法相比,该方法大大减少了计算量;第2种预测方程改进方法.文献[3]将鲁棒控制加入模型预测中,通过改进模型预测的方程来提高鲁棒性,但该文献只考虑了电感的变化,忽略了电阻和磁链的摄动,并且在改进方程引入了权重系数,增加了设计难度.文献[4]采用增量式电流预测控制,消除了永磁体参数的影响,并用扩展状态观测器补偿电感扰动,但该文献同样没有考虑到电阻的变化;第3种控制器补偿.文献[5]将滑模控制器嵌入到模型预测控制中,把标称参数预测的电压当作等效控制,通过引入一个滑模修正项,增强了系统的参数鲁棒性;第4种干扰估计补偿.此方法研究受到了最多的关注,其基本思想是通过设计一个观测机制来估计扰动与不确定性变量,然后将估计到的干扰补偿到预测控制器中.通过使用扰动观测器(disturbance observer,DO),扩张状态观测器(extended state observer,ESO),滑模观测器(sliding mode observer,SMO),进行扰动估计,并补偿到控制器中[6–10].文献[6]基于DPCC模型,设计了改进的线性DO,使系统具有更好的电流测量噪声抑制效果.文献[7]构造线性ESO和文献[8]非线性ESO,对参数变化进行了补偿.文献[9]采取新型趋近律设计滑模观测器,来估计定子电流预测值和参数失配引起的系统扰动.文献[10]对转速离散方程进行二阶展开后再采用滑模观测器,提高了q轴参考电流的精度.

为了提高DPCC控制系统参考电流的精度,需要对电机的转速环进行鲁棒控制设计.在鲁棒控制方法中,滑模控制(sliding mode control,SMC)由于对不确定性和干扰不敏感,被认为是处理不确定非线性系统最有效的方法之一.研究人员分别设计了新型的滑模趋近律并应用到电机控制中,减小了抖振并加快了收敛速度[11–14],但文献[13]并未在真实的电机上进行实验.文献[15]将DO与超螺旋滑模技术相结合提高了永磁同步电动机速度环的控制性能,通过干扰估计补偿以及高阶滑模的方法减小了滑模抖振.文献[16]提出了一种终端滑模控制方法,在滑模面引入非线性项,使系统跟踪误差在有限时间内达到平衡点.然而,该方法在平衡点附近仍然存在奇异性问题.针对上述问题,文献[17]和文献[18]设计了非奇异终端滑模速度控制器,其中文献[18]将非奇异快速终端滑模面结合新型趋近律,但控制器参数较多,增加了系统的复杂性.

综上分析,本文设计一种基于DPCC永磁同步电机驱动系统的滑模控制方案.首先,电流环采用无差拍预测电流控制,可以提高控制带宽和跟踪精度.其次,为克服电流环中参数失配问题和抑制速度环中参数和负载的干扰,分别构造两个三阶超螺旋滑模观测器(super-twisting sliding mode observer,STSMO),并通过前馈方法将相应的估定值补偿到闭环控制中.为了提高速度环的动态响应和鲁棒性,采用了一种改进趋近律的控制策略,它可以适应滑动面和系统状态的变化,以减少抖振和趋近时间.最后,在内置式永磁同步电机测试平台进行了实验研究,实验结果表明所提出的控制策略能够在包含负载变化及参数不确定性的永磁同步电机驱动系统中实现快速的动态响应和优异的稳态性能.

2 预备知识

2.1 PMSM数学模型

内置式PMSM(interior PMSM,IPMSM)在dq坐标系下的定子电流方程为

电磁转矩方程

运动方程

其中:ud,uq,id,iq分别为dq坐标系下的定子电压和定子电流;R为定子电阻;Ld,Lq分别为dq轴电感;ωe为电角速度;ψf为转子永磁体磁链幅值;Te为电磁转矩;Pn为磁极对数;ωm为机械角速度;TL为负载转矩;B为摩擦系数;J为转动惯量.

2.2 三阶超螺旋滑模观测器

观测系统的状态方程定义为

其中:x1为状态变量;x2为未知扰动;u为控制输入;f(t)为扰动的导数,且f(t)的导数也是有界的,表示为

根据式(4),设计三阶超螺旋滑模观测器形式如下:

其中:k1,k2,k3>0为观测器增益,带有符号的变量代表相应的估计值.各自的估计误差定义为

将式(6)减去式(4),可以得到误差方程为

根据文献[19–20]中的参数选取办法,选择合适的增益,e1,e2,e3将在有限时间内收敛到零.

3 基于观测器的无差拍预测电流控制器设计

3.1 无差拍预测电流控制

应用前向欧拉法对式(1)中所示的模型进行离散化,PMSM的离散电流模型可以表示为

其中Ts为采样周期.

在传统的DPCC方法中,根据离散预测模型式(9),在一个调制周期后,使实际电流矢量达到参考电流即i(k+1)=i∗(k+1),此时定子电压表达式如下:

输出的定子电压矢量使实际电流矢量接近预期值.由式(10)可知,预测控制包括3个参数(定子电阻、定子电感和永磁链),这意味着预测电流控制是一种基于模型的方法.因此,预测模型的参数精度对于PMSM系统的控制性能非常重要.

随着电机运行或外部条件的变化,控制器中设置的参数可能与实际不同.包含参数不确定性的电压方程表示为

其中:fd,fq为参数扰动,表达式如下:

其中:∆R,∆Ld,∆Lq,∆ψf为定子电阻、电感和永磁体磁链实际值与标称值之间的误差.关于参数变化对DPCC系统的影响在文献[9–10]中进行了详细的分析,本文不再赘述.

3.2 基于三阶超螺旋的滑模观测器

为了达到参数扰动估计和电流预测的目的,设计高阶滑模观测器表达式如下:

其中:ed=-id,eq=-.用式(13)与式(14)分别和式(11)相减,误差方程为

利用前向欧拉法,推导出式(13)–(14)的离散时间方程

为了更好的理解所设计电流环STSMO,以d轴STSMO为例画出其控制框图,如图1所示.

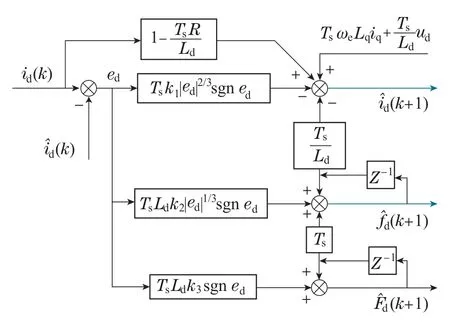
图1 d 轴STSMO控制框图Fig.1 The control block diagram of the STSMO for d-axis

4 基于改进滑模算法的速度控制器设计

4.1 基于三阶超螺旋滑模速度扰动观测器

考虑参数摄动和外部负载扰动,且采用最大电流转矩比控制策略,式(3)可以改写为

式中d为参数摄动和外部负载的总扰动.按照式(6)设计速度环扰动观测器

式中:ewd=-d,Dwd=-D,D为d的导数.根据文献[19–20]中的参数选取办法选择合适的观测器增益,观测的速度和扰动的误差可以在有限时间内收敛到零.

为了在数字系统中实现,需要对观测器方程式(21)进行离散化

为了更好的理解所设计速度环STSMO,画出其控制框图,如图2所示.

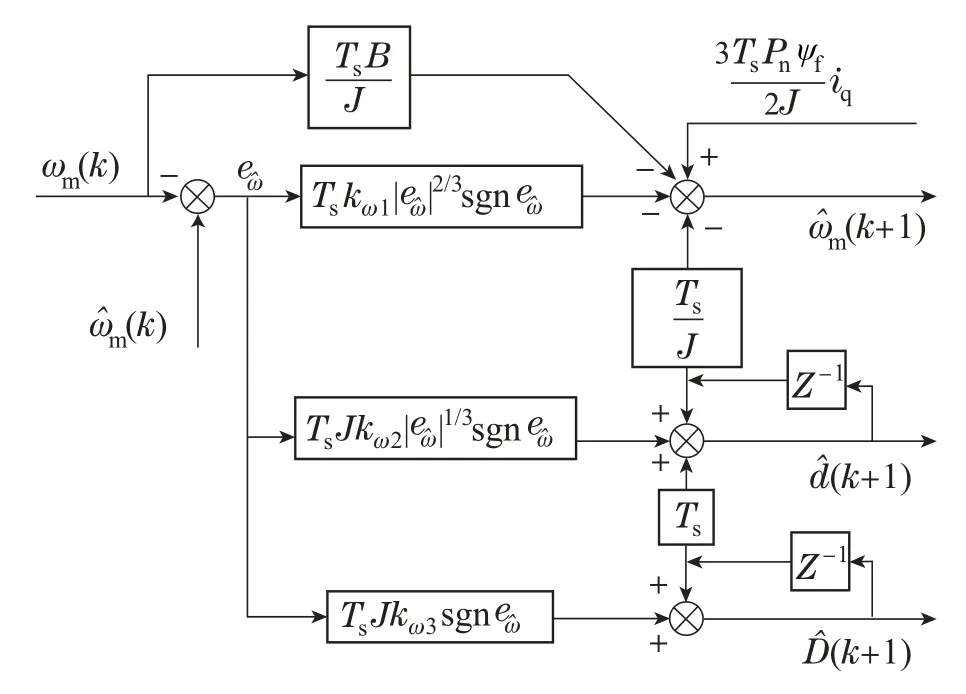
图2 速度环STSMO控制框图Fig.2 The control block diagram of the STSMO for speed loop

4.2 滑模速度控制器设计

定义滑模面为

其中ew为转速误差,定义为

传统的指数趋近律为

其中:η>0,q>0.选取合适的η,q可以使系统趋近滑模面,并在滑模面上运动,且其取值越大,系统的收敛速度越快,但系统抖振现象也会更显著.为了减小抖振,本文采用一种改进新型指数趋近律[18]

式中:ks>0,kt>0,δ>0,0<ε<1.当系统远离滑模面时,符号函数前面的系数趋近于ks|e|/ε,其值大于ks,加快了收敛速度.当系统到达滑模面时,符号函数前面的系数趋近于ks|ew|,其值小于ks以限制抖振.

结合式(20)(23)(27),并将观测的扰动d补偿到控制律中,可得速度控制律为

4.3 稳定性证明

为证明上述算法的稳定性,选取李雅普诺夫函数如下:

对V求导可得

将式(27)代入式(30)中可得

依据LaSalle引理[21],所设计的滑模控制器是指数收敛的.

所提出的基于高阶滑模观测器的永磁同步电机无差拍预测电流系统控制框图如图3所示.

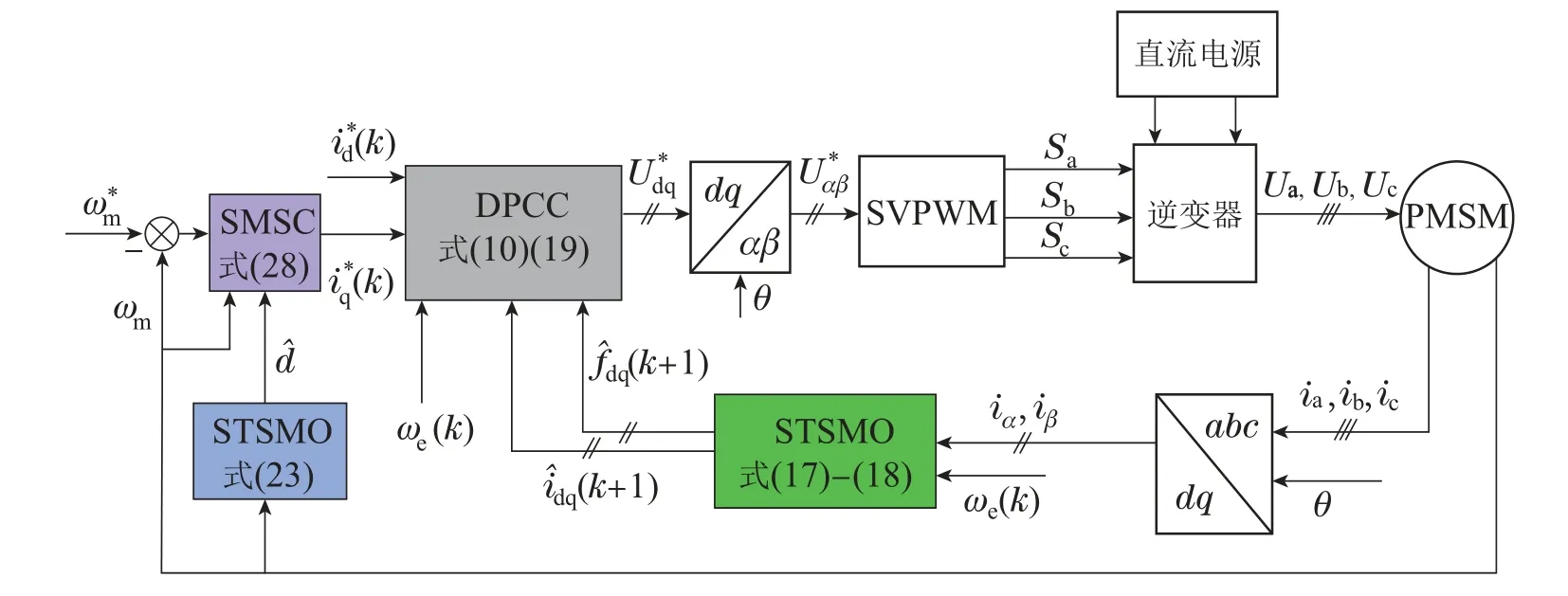
图3 系统控制框图Fig.3 The control block diagram of the system

5 实验验证

在图4展示的实验平台上进行研究,装置主要包括被测电机(内置式永磁同步电机)、负载电机、逆变器、变频器、dSPACE1202板卡、示波器及电脑端Control Desk 软件.开关频率设置为10k Hz,采样周期为100µs.被测电机参数如表1所示.

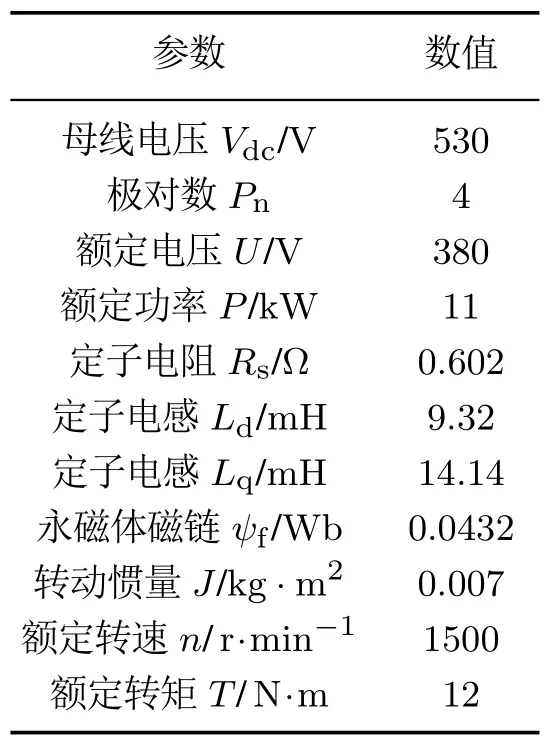
表1 内置式永磁同步电机参数Table 1 IPMSM parameters

图4 实验平台Fig.4 Testbed prototype

为验证所提算法的合理性和有效性,在dSPACE 1202实验平台上搭建了5个PMSM驱动系统.系统1:速度环采用比例积分(proportion integration,PI)控制,电流环采用传统的无差拍预测电流控制;系统2: 速度环采用PI控制,电流环采用无差拍预测电流控制并利用本文所设计的电流环STSMO进行扰动补偿;系统3:速度环采用传统指数趋近律的SMC,电流环与系统2相同;系统4: 速度环采用本文所设计新型趋近律的SMC,电流环与系统2相同;系统5: 在系统4的基础上利用本文所设计的速度环STSMO 进行扰动观测并补偿.为了体现对比的公平性,系统1与系统2采用参数相同的PI控制器.

实验对比分为3个部分: 第1部分为系统1与系统2进行控制效果对比,旨在体现本文所设计的电流环STSMO可以估计未来电流值和参数失配引起的集中扰动,并有效地消除参数失配的影响;第2部分为系统3与系统4进行控制效果对比,旨在体现本文所设计新型趋近律速度控制器与传统滑模速度控制相比,其具有自适应趋近律,以减少抖振和趋近时间,并具有良好的抗扰能力;第3部分为系统4与系统5控制效果对比,旨在体现本文所设计的速度环STSMO可以估计速度环参数摄动和负载转矩扰动,提高速度的跟踪精度和抗扰性.

5.1 系统1与系统2控制效果对比

由于在真实电机实验中不能随意改变参数,因此在控制器(dSPACE1202)中设置参数变化.根据文献[9]设置参数变化,电阻变为标称参数的10倍和0.1倍,电感变为标称参数2倍和0.5倍,磁链变为标称参数的4倍和0.25倍.

电机空载启动,给定转速为1500 r/min,并在运行过程中负载转矩突变为12 N·m.转速环控制参数为kp=0.12,ki=4.电流环观测器控制参数为k1=50000,k2=100000,k3=1000000,k4=50000,k5=100000,k6=1000000.

在图5–6可以看到,电阻的变化对于系统的电流的影响并不明显,但当电感和磁链变化时,系统1的电流脉动变大,跟踪精度下降.且在磁链变化时最为明显,电流iq完全跟踪不上.系统2在电阻、电感、磁链发生变化时,较系统1表现出更好的动态和稳态性能.

图5 系统1在电阻、电感、磁链摄动下的电流响应Fig.5 The current responses of system one under the perturbations of resistance,inductance and flux linkage

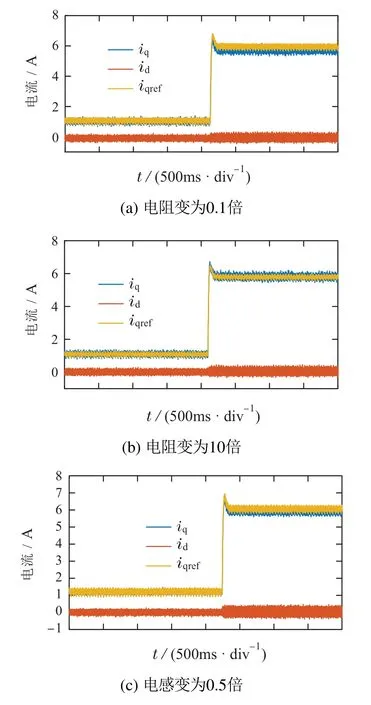
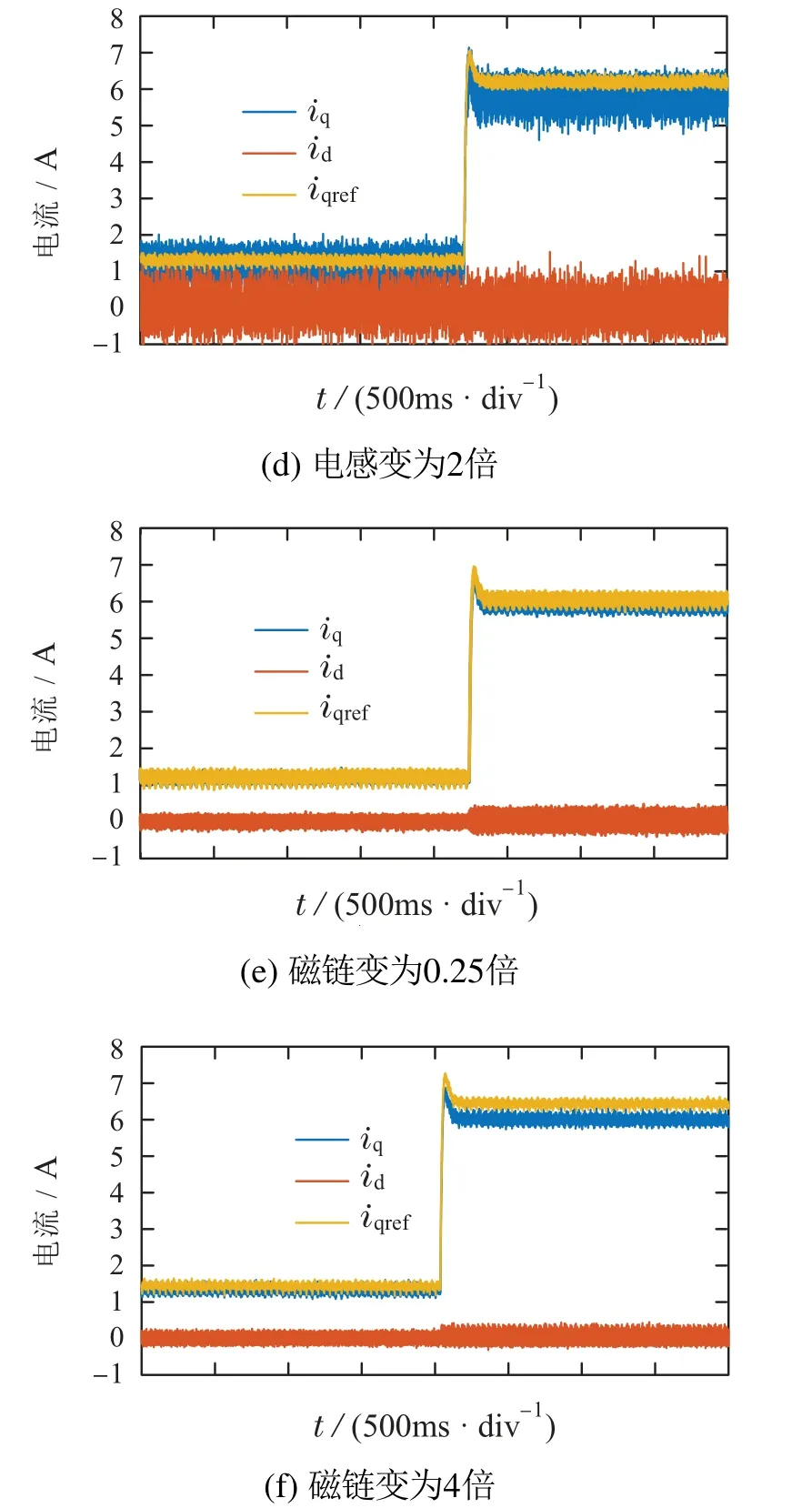
图6 系统2在电阻、电感、磁链摄动下的电流响应Fig.6 The current responses of system two under the perturbations of resistance,inductance and flux linkage

在参数摄动的情况下,DPCC方法的d轴和q轴电流响应明显存在稳态误差.此外,通过表2进行定量比较可以清楚地看出,采用所提出的DPCC+STSMO方法可以有效地抑制稳态误差的影响.

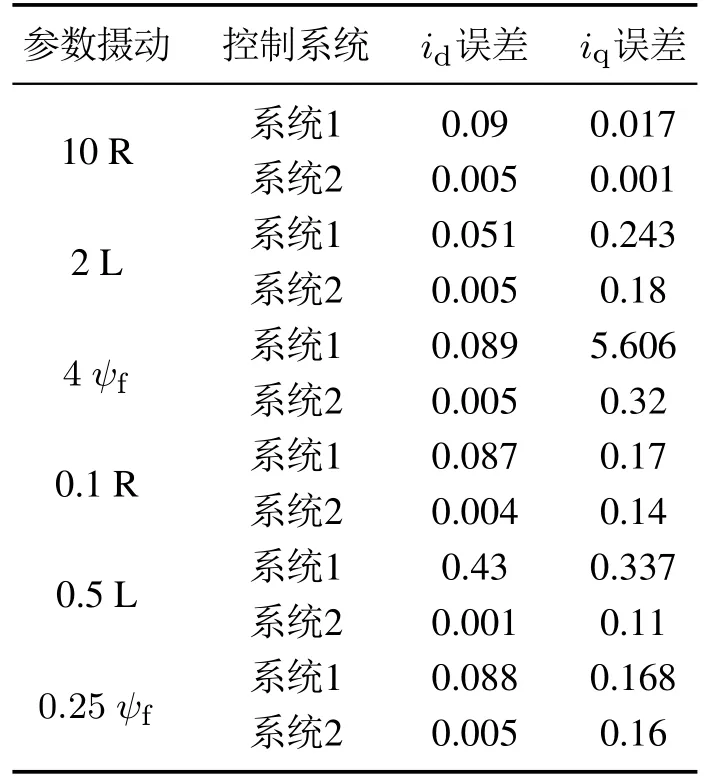
表2 电流控制器实验效果对比Table 2 Comparison of experimental effects of current controller

5.2 系统3与系统4控制效果对比

系统3采用的指数趋近律控制参数为c=5,η=250,q=400.系统4采用的新型趋近律控制参数为ks=180,kt=400,ϵ=0.6,δ=8.电机空载启动,给定转速为1500 r/min,并在运行过程中负载转矩突变为12 N·m.

由图7–8可以看出,在负载发生变化时,系统4较系统3更快的恢复到给定转速值.

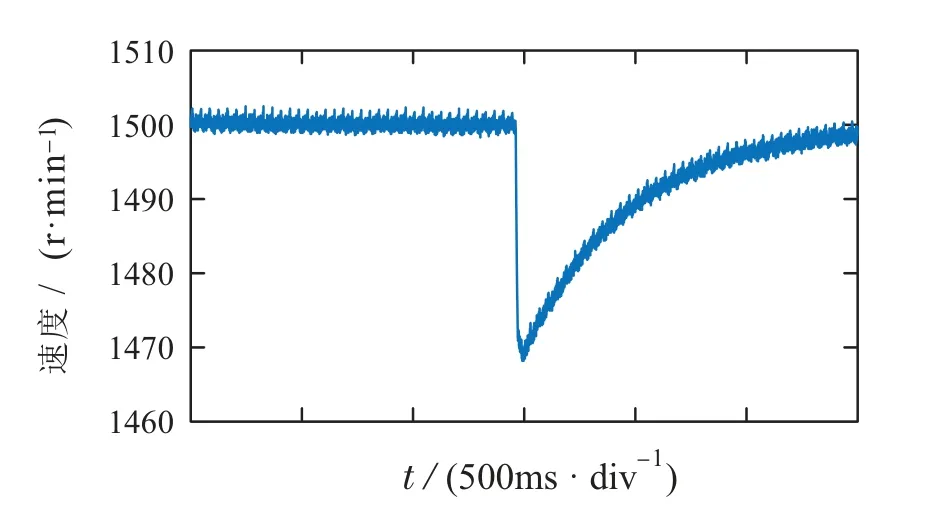
图7 系统3的速度响应Fig.7 The speed response of system three

图8 系统4的速度响应Fig.8 The speed response of system four

5.3 系统4与系统5控制效果对比

电机空载启动,给定转速为1500 r/min,并在运行过程中负载转矩突变为12 N·m.速度环观测器参数为kw1=11000,kw2=14000,kw3=15000.

由图9可知,系统5在负载发生变化时,转速的调节时间更小,且转速跌落也更小.实验表明本文所设计的系统具有更好的动态和稳态性能.在表3中可以看到系统5的跌落速度是最小的,且恢复时间远小于系统3和系统4.

表3 速度控制器实验效果对比Table 3 Comparison of experimental effects of speed contr oller

图9 系统5的速度与电流响应Fig.9 The speed and current responses of system five

6 结论

本文提出了一种基于高阶滑模观测器的无差拍预测电流控制方法.首先,本文所设计的3阶超螺旋滑模观测器可以准确估计在电阻、电感、磁链参数发生摄动时的扰动并前馈给DPCC,提高了系统的鲁棒性.其次,基于改进的趋近律滑模设计了电机的速度环控制器,并利用3阶超螺旋滑模观测器估计速度环扰动,使电机在发生负载突变时有更少的调节时间和更强的抗干扰能力.实验结果表明,相比较于传统控制方法,该控制策略可以在负载和参数变化的情况下,具有更好的控制表现.