基于预见与PI补偿的不确定非线性系统鲁棒滑模控制

兰永红,吴瑾怡 ,周宇玺

(1.湘潭大学自动化与电子信息学院,湖南湘潭 411105;2.五凌电力有限公司,湖南长沙 410000)

1 引言

近年来,不确定非线性系统的鲁棒控制问题受到国内外众多学者的广泛关注,滑模控制对系统参数摄动以及外部干扰具有良好的适应性和较强鲁棒性,是实现不确定非线性系统鲁棒控制的有效方法之一[1–2],并成功运用于电力系统[3]、机器人[4]等控制领域.为了在快速到达滑动模态的同时能消除滑模运动阶段的抖振,文献[5]提出了趋近律方法,其中,等速趋近律、指数趋近律和幂次趋近律存在一定程度的缺陷.因此,文献[6]提出了一种快速收敛的双幂次趋近律,综合了指数趋近律和幂次趋近律的优点,该方法消除了抖振,加快了远离滑模面时的趋近速度.

另一方面,在很多伺服系统中,未来一段时间的目标参考或干扰信号是可预见的.预见控制正是一种利用系统已知参考目标或干扰信号的未来信息,以改善系统动态响应、抑制外界扰动、提高系统跟踪精度的控制方法[7–8],近年来,预见控制已经广泛应用于自动驾驶、航天飞行器、机器人等伺服领域[9–11].从实用角度来看,数字预见控制更易于实现.考虑到连续系统和离散系统的稳定性条件差异,对连续系统的预见控制研究仍有必要.

连续系统的预见控制问题是基于最优控制,从而研究非自治系统的稳定性问题.基于预见控制思想,文献[12]提出了基于线性连续时滞系统,并能在有限时间内有界跟踪的一类控制问题.针对一类参数变化的线性系统,文献[13]提出了一种基于降阶估计的容错预见控制的设计方法.在此基础上,文献[14]基于重复控制的设计方法,通过构造增广系统,设计了线性连续系统的基本型预见重复控制器.文献[15]进一步将结果推广至线性连续时滞系统.

基于预见补偿的滑模控制不但能有效克服系统的不确定性,而且能提高控制系统跟踪精度,具有较强的鲁棒性.文献[16]针对船舶自动操纵系统设计了自适应滑模预见控制器,减小了传统滑模控制中的暂态超调,保持了不确定船舶动态系统的控制性能.对于智能电动汽车的目标路径的精确跟踪问题,文献[17]提出了一种基于滑模控制的预见控制器的设计方法,提高了识别精度,且可以更好的跟踪所需轨迹.文献[18]提出了最优积分滑模预见控制器的设计方法,并采用积分滑模控制对最优预见控制器进行鲁棒控制.文献[19]针对一类连续时间线性系统,设计了具有预见补偿的滑模控制器,保证了系统的鲁棒性.需要指出的是,针对不确定非线性连续系统的预见控制器设计问题,其相关报道在国内外都较少见.

受以上文献的启发,本文针对一类不确定非线性系统,研究基于预见与比例–积分(proportional-integral,PI)补偿的鲁棒滑模控制设计问题.本文主要贡献如下: 1)针对不确定非线性被控对象,提出了一种具有预见与PI补偿的滑模控制系统结构,并将控制器的设计问题转化为一类增广系统的稳定性问题;2)基于最优控制理论,设计标称增广系统的最优预见PI控制器.针对不确定增广系统,采用变结构控制思想,设计了积分滑模预见控制器;3)通过选择合适的PI控制器增益,所设计的集成控制器包含了已有文献的结果.

2 问题描述

考虑如下的非线性系统:

其中:x(t)∈Rn,u(t)∈Rm,y(t)∈Rq,d(x(t),t)∈Rp分别为系统的状态、控制输入、系统输出和外部干扰.A,B,C,D是具有合适维数的常数矩阵,∆A和∆B是不确定性矩阵.

对被控系统(1)及给定参考输入信号r(t)作如下假设.

假设1矩阵(A,B)可控,(A,C)可观.

假设2参考输入信号r(t)∈Rq是分段连续可微函数,其可预见步长为lr,即在t≤θ≤t+lr的任意时间θ,r(θ)已知.

假设3不确定性矩阵∆A,∆B和外部干扰d(x,t)满足匹配条件

根据假设3,系统(1)可以写成

本文提出的控制系统结构框图如图1所示,其中CR为PI控制器,NL(t)为预见控制器,CSMC为滑模控制器,控制对象如系统(1)所示.本文的目的是设计一种具有预见与PI补偿的鲁棒滑模控制器u(t),使闭环系统(1)的输出y(t)在稳定状态下,无静态误差的跟踪参考输入r(t),即

图1 具有预见与PI补偿的滑模控制系统框图Fig.1 Block diagram of sliding mode control system with preview and PI compensation

且性能指标函数(4)具有最小值,

其中:Qe∈Rq×q,R∈Rm×m为对称正定矩阵.

注1类似文献[20–21],控制系统前馈通道引入PI控制器以减小闭环系统的稳态误差.此外,为进一步提高系统的跟踪性能,前馈通道还引入了预见补偿.这是本文主要创新之一.

3 控制器设计

图1中,PI控制器的时域形式为

其中kp,ki为PI控制器增益.

构造如下增广状态向量z(t):

结合式(2)和式(5),可得

3.1 最优预见PI控制器设计

本节针对标称系统,基于最优控制原理,设计一个最优预见PI控制器.为此,令(t)=0,系统(7)可简化为

针对系统(8),构造如下性能指标函数:

为了得到控制系统最优预见PI控制器存在的必要条件和系统的相关参数,给出如下引理.

且K=[KxKeKv]是如下代数黎卡提方程(algebraic riccati equation,ARE)的解:

证根据最优控制理论,定义Hamilton函数

其中λ(t)是伴随向量.由最优控制极小值原理,有

由此可知系统的最优控制律为

闭环系统动态方程为

其中K(t),g(t)满足

对于线性定常系统,λ(t)与z(t)之间满足如下关系:

由式(14)–(17),可知

对于t∈[t,tα],对式(19)求解并积分,有

联立式(13)(15)(20)可得

其中K=[KxKeKv].

在[-L,t](L>lr)上对式(21)积分,并注意到对于t≤0有x(t)=0,u(t)=0,r(t)=0,由此可得

证毕.

注2注意到预见项f(t)中,矩阵Hurwitz稳定,从而f(t)单调递减.可见,随着预见步长的增加预见信息逐步减弱.对于预见步长的选取,可通过性能指标函数值J的衰减变化阈值得到控制器合适的预见步长[21].此外,性能指标中的权重矩阵主要通过试凑法进行选取.在最近的研究中,已经提出了各种优化算法,来解决线性二次型调节器(linear quadratic regulator,LQR)问题权重矩阵的选择这个问题.例如基于动态矩阵控制算法的LQR[22]和基于粒子群算法的LQR[23].

3.2 滑模控制器设计

本节针对不确定系统(1),引入积分滑模面,设计一种具有鲁棒性能的预见控制器.

针对增广系统(7),构造如下积分滑模面:

其中:u0如式(22)所示,为常数矩阵且满足条件G非奇异.

注3类似文献[24],滑模面(25)包含了控制输入的导数.该滑模面获得的等效控制输入一方面可补偿匹配的不确定性;另一方面,可确保稳定状态.因此,该滑模面是最优的.

当系统进入滑动模态后,满足s(t)=0,(t)=0.因此

由式(24)可得滑模等效控制律为

将式(25)代入增广系统(7),并利用式(14),可得滑动模态方程为

对比系统(26)和系统(15)可以看出,不确定系统的滑动模态方程和标称系统的最优闭环系统动态方程完全一致.因此,系统(26)所描述的滑动运动系统渐近稳定,且滑模面(23)对系统不确定性和外界干扰具有鲁棒性,是鲁棒最优滑模面.

本文考虑如下双幂次滑模趋近律[25],通过调整趋近律的参数,来减弱抖振:

式中:α>1,0<β<1,ε1>ω>0,ε2>0.

在双幂次趋近律(27)中,当系统远离滑动模态时,-ε1|s(t)|αsgns(t)起到主要作用;当系统靠近滑动模态时,-ε2|s(t)|βsgns(t)起到主要作用.因此,双幂次趋近律不仅可以有效的消除抖振,而且具有较快的收敛速度.

定理1对于不确定系统(1),对给定的PI控制增益,图1所示的控制系统的最优预见PI滑模控制器为

Fx,Fe,Fv由引理3给出,

证选择李雅普诺夫函数

根据滑模可达性,结合趋近律(27),可知

由此可得

因此,滑动模态在有限时间内能到达平衡零点.

滑模控制器的线性部分如式(10)所示.对于积分滑模面(23)和双幂次趋近律(27),可得控制器中非线性部分

综合式(10)和式(31),即可得最优预见PI滑模控制器(28).证毕.

注4具有预见与PI补偿的鲁棒滑模控制器(30)由5部分组成: 第1部分是状态反馈控制器,用来提高每个周期内系统的稳定性;第2部分是PI控制器,用来改善控制系统的稳态性能;第3部分是误差积分补偿器,用于消除静态误差;第4部分是预见补偿控制器,以提高闭环系统的跟踪性能.第5部分是滑模控制器,用来调节系统的鲁棒性.

另一方,根据帕德近似[26],易知

为方便计算,取近似值

近似等效[27–28].式(36)的时域形式为

其中:e(t)为控制系统的跟踪误差;L为时滞环节的延迟时间,其周期与参考输入信号r(t)一致[28].

由上述分析并结合定理1,有如下推论.

推论1对于不确定系统(1),图2所示的控制系统在最优滑模预见重复控制器

图2 滑模预见重复控制系统框图Fig.2 Block diagram of sliding mode preview repetitive control system

的作用下,跟踪误差鲁棒渐近稳定,其中:

Fx,Fe,Fv,f(t),u1(t)由引理3给出,v(t)如式(37)所示.

4 数值仿真

设线性不确定系统(1)具有以下参数:

外部非线性干扰信号和参考输入信号r(t)为

经过反复对比测试,性能指标函数(9)的权重矩阵取为

时,系统输出响应具有较小的超调量和较快的响应速度.

应用定理1,利用MATLAB求解,可求得如下控制器增益:

参考输入信号r(t)的周期L=10,因此,令PI控制器的增益为

通过二次型性能指标最优法[5],积分滑模面参数可设计为

为了说明预见步长对系统输出的影响,系统仿真结果如图3–4所示.不同的预见步长下的闭环系统跟踪误差的最大峰值如表1所示.不同预见步长时,y(t)都能精准的跟踪r(t),当预见步长变长,超调量减小,此时,y(t)能更精准的跟踪r(t).值得注意的是,在预见步长达到某个阈值后,预见补偿影响甚微.这与文献[7]中的结论一致.

表1 系统跟踪误差Table 1 System tracking error

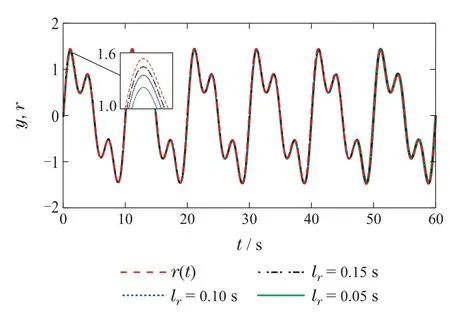
图3 不同预见步长下系统输出响应Fig.3 System output responses with different preview steps

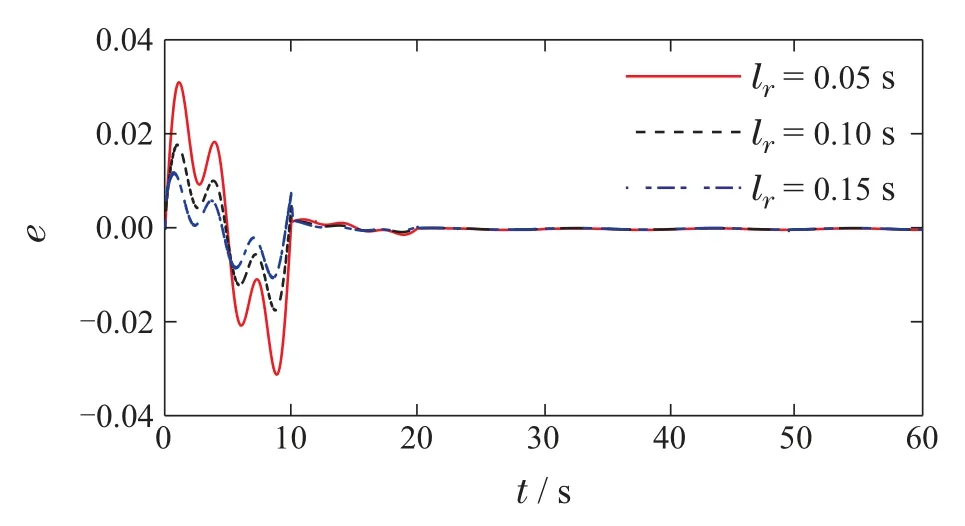
图4 不同预见步长下跟踪误差Fig.4 Tracking errors with different preview steps

为说明本文所提控制方法的有效性,将其与文献[20]提的基于PI+等价输入干扰(equivalent-input-disturbance,EID)控制方法进行对比.仿真结果如图5–6所示,系统跟踪误差的最大峰值如表1所示.由仿真结果可见,本文所提控制方法具有更优的跟踪性能.

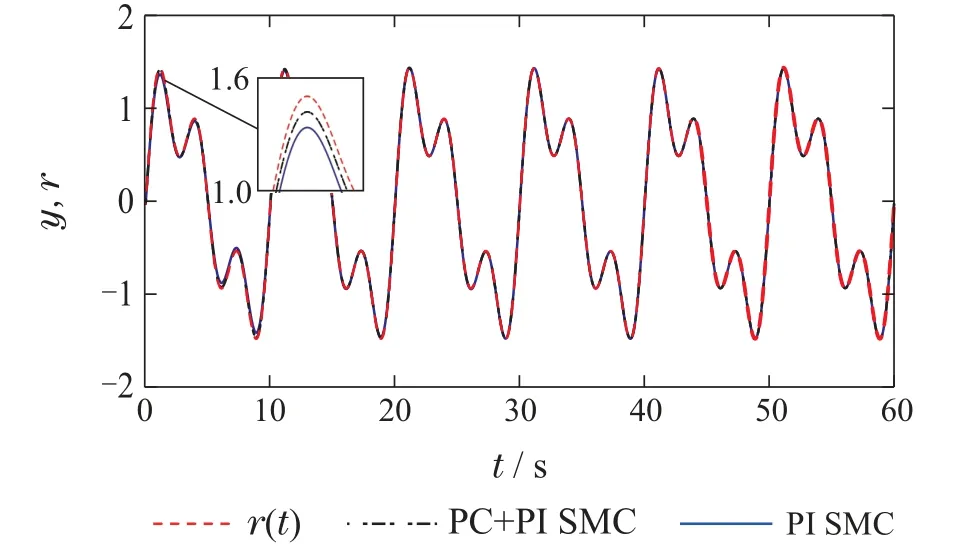
图5 不同控制方法下系统输出响应Fig.5 System output responses with different control methods

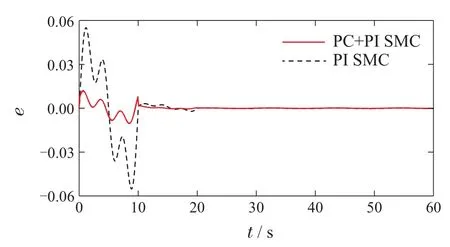
图6 不同控制方法下跟踪误差Fig.6 Tracking errors with different control methods

为了说明不同滑模趋近律对系统的影响,给定预见步长lr=0.15,分别对以下3种不同的趋近律:

所设计的预见滑模控制器进行对比.仿真结果如图7–8所示.系统跟踪误差的最大峰值如表2所示.

表2 不同滑模趋近律下的系统跟踪误差Table 2 Tracking errors with different sliding mode

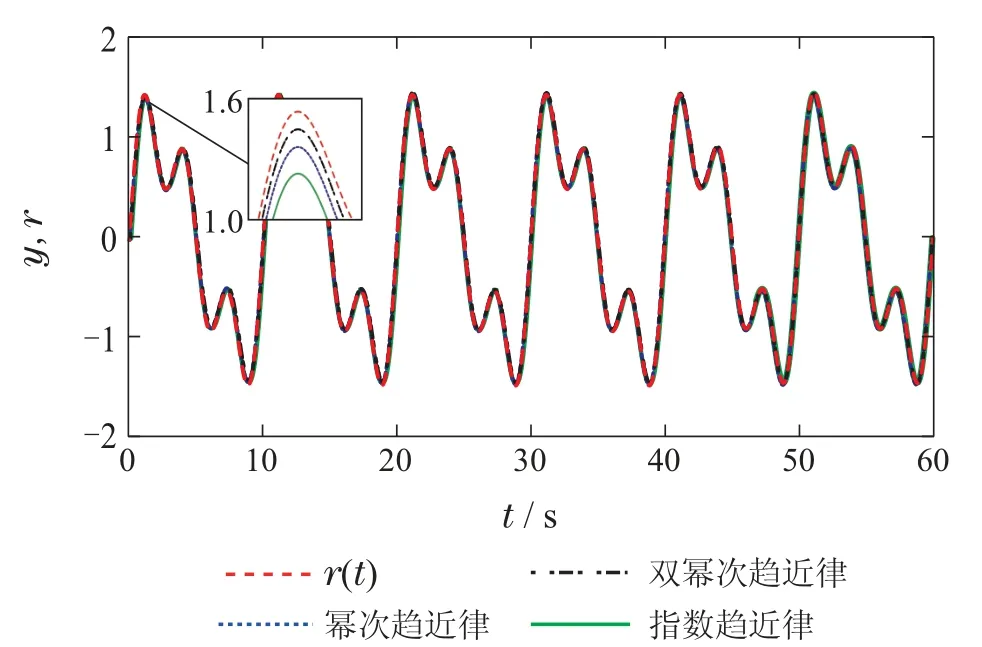
图7 同滑模趋近律下系统输出响应Fig.7 System output responses with different sliding mode reaching laws

由图7–8可知: 指数趋近律由于含有常数项,在远离滑动模态阶段收敛速度过小,导致收敛时间过长;幂次趋近律尽管收敛速度高于指数趋近律,但效果不明显;双幂次趋近律收敛速度明显高于指数趋近律和幂次趋近律,具有更好的运动品质.图8为跟踪误差的动态收敛过程,表明滑模变结构控制可以保证系统的稳态性、鲁棒性.

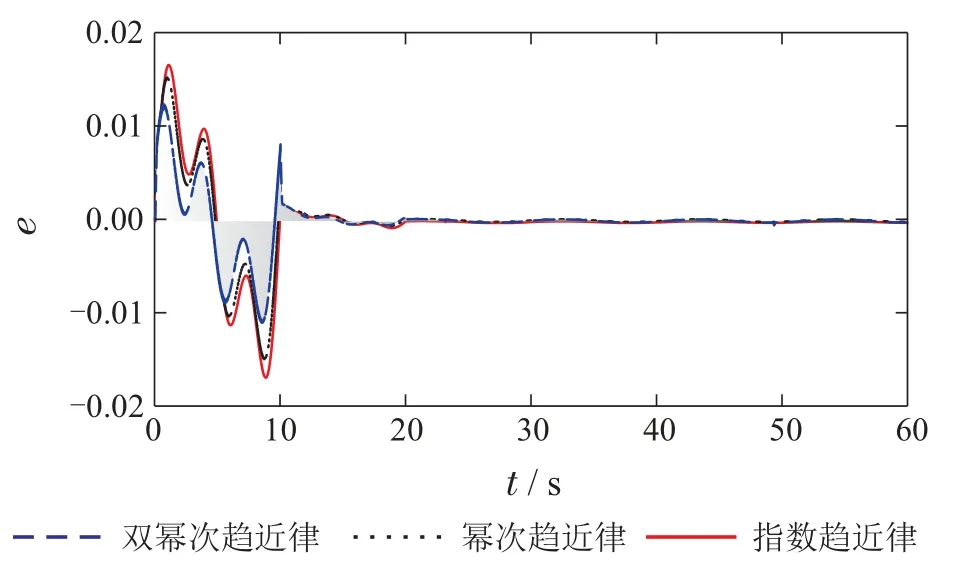
图8 不同滑模趋近律下跟踪误差Fig.8 Tracking errors with different sliding mode reaching laws

5 结论

本文针对一类匹配不确定非线性连续时间系统,研究了一种基于预见与PI补偿的鲁棒滑模控制设计方法.通过构造一个包含可预见的目标信号的不确定增广系统,根据最优控制理论和积分滑模控制和最优预见PI控制方法,设计不确定增广系统的基于积分滑模控制和最优预见PI 控制的集成控制器.如何进一步优化控制器参数,并对于不确定非线性时滞系统,设计一种基于高阶滑模的预见控制器,将是进一步研究的难点.