基于近端凸差分方法的多层卷积变换学习算法

郭泳澄 ,唐健浩 ,李珍妮†,吕 俊

(1.广东工业大学自动化学院,广东广州 510006;2.广东省物联网信息技术重点实验室,广东广州 510006)

1 引言

近年来,稀疏表示受到越来越多学者的关注与研究,并在信号处理、机器学习、人工智能等领域成功得到了广泛的应用[1–5].稀疏表示模型主要有两大类,一种是字典学习(dictionary learning,DL)[6–8],通过从信号学习一个过完备字典,并用字典中尽可能少的原子的线性组合表示原始信号,达到对原始信号稀疏表示的目的.然而,字典学习模型的稀疏编码问题是一个NP-hard难题[9],通常需要采用贪婪算法等方法近似求解[10–11],需要付出较大的计算代价;另一种是变换学习(transform learning,TL)[12–14],通过从信号学习得到的变换基直接作用于信号提取特征,并对特征进行稀疏约束完成对信号的稀疏表示.字典学习与变换学习都属于传统的基于块的稀疏表示模型,即受限于字典或变换基的大小在处理信号时需先将一完整信号提取为多个小尺寸的重叠信号块,然后对这些信号块分别进行稀疏表示,最后再将得到的稀疏特征重新合成得到完整信号的稀疏特征.这种分块处理的方法导致在稀疏编码过程中忽视了块与块之间的相关性与连续性,并且在处理大规模数据时,需要大量的内存空间用于存储大量的信号块,导致算法的使用受限.

近期,随着卷积神经网络(convolutional neural network,CNN)的快速发展以及在各种类型数据分析取得的成功,同时为了解决传统变换学习模型的缺陷,研究者将卷积神经网络与变换学习相结合,提出了卷积变换学习(convolutional TL,CTL)[15–18].CTL将卷积神经网络的卷积操作融入了变换学习模型,通过学习一组平移不变的卷积核代替原来的变换基,直接对原始信号进行卷积提取特征.与传统基于块的变换学习模型相比,CTL体现出以下几大优势: 1)解决了传统变换学习对信号块之间相关性与连续性的忽视问题,在信号处理过程中充分保留了原始信号的完整内部结构;2)通过对信号整体特征的稀疏约束,避免了稀疏编码的高度冗余;3)直接处理原始信号而不需要截取和存储大量的信号块,适合用于处理大规模数据,拓展了传统变换学习的应用场景.

目前,与传统稀疏表示模型相比兼具高性能与高效率特点的CTL开始逐渐吸引学者们的研究.已有的CTL稀疏表示方法有基于ℓ0范数与基于ℓ1范数稀疏约束的CTL两种,2018年,Maggu 等[15]首次将卷积操作融合进了变换学习,提出了基于ℓ1范数的CTL,应用于人脸图像的稀疏特征提取与分类任务,并与传统稀疏表示方法进行实验对比,验证了CTL算法的优越性.Chun等[16–17]使用ℓ0范数作为稀疏约束,提出了卷积解析算子学习(convolutional analysis operator learning,CAOL),在CT图像的重构任务上取得了优秀的效果.随后,Gupta等[18]用无稀疏约束的CTL训练一维卷积核,搭建了处理股票回归预测任务的多层框架.

然而,在图像稀疏特征的提取方面,目前仅有文献[15]提出的基于ℓ1范数的CTL稀疏特征提取模型.ℓ0范数与ℓ1范数是稀疏表示领域常用的稀疏约束方法,其中ℓ0范数是最直接的稀疏约束方法,通过约束特征中的非零元素数量来达到稀疏约束的效果,然而ℓ0范数的求解是一个NP-hard优化难题,随着矩阵维度的增加求解计算量呈指数级增长,在多项式时间内只能找到次优解[19].因此,常用的一种解决方法是通过采用贪婪算法(如正交匹配追踪[20]、硬阈值法[21]等)选择局部最优值对ℓ0范数求近似解,但是此类求取近似解的方法通常难以使稀疏表示模型得到精确度足够理想的稀疏特征.另一种常用的方法则是使用ℓ1范数代替ℓ0范数的方法来求取ℓ0范数的凸松弛解[22],因为ℓ1范数的求解是一个凸优化问题,求解计算量与矩阵维度为线性关系,通过采用软阈值法可以简单求得封闭解,虽然相比于直接对ℓ0范数求解有效降低了计算复杂度[20],但是ℓ1范数存在稀疏度不足和大元素过度惩罚的缺陷[23–24],同样容易导致模型获得的稀疏解精确度不足的问题.近年,有研究者提出使用非凸log正则化函数作为稀疏约束[25],并且证明了相较于ℓ1范数,log正则化在获取强稀疏解的同时可以有效缓解大参数过度惩罚的问题,有效减小稀疏解的误差.然而,目前还没有关于使用log正则化作为卷积变换学习特征提取稀疏约束方法的研究.根据以往的稀疏表示理论与文献研究表明,稀疏特征的稀疏性与精确性是影响稀疏特征质量的重要因素,在获取高稀疏解的同时减小稀疏特征与原始信号的偏差,是提取高质量高精度稀疏特征的关键,也是提升稀疏表示模型性能的关键.而对于信息丰富复杂的输入信号,单层的稀疏表示模型难以有效提取信号的深层语义信息,获取更具鉴别性的深层稀疏特征的能力受限.因此,研究稀疏性更强、精确度更高的多层CTL稀疏表示方法是其进一步提升和开发的一个关键的研究点.

针对上述问题,本文提出了一种基于log正则化函数的多层CTL稀疏表示模型.通过搭建多层的CTL稀疏特征提取框架,对单层的CTL稀疏特征进行进一步深层次的稀疏编码,从而从输入信号提取更具鉴别性与深层语义信息的稀疏特征.同时,针对现有的基于ℓ0范数与基于ℓ1范数的CTL算法所使用的稀疏约束方法难以有效获取具有高精确度的稀疏特征问题,本文使用稀疏度强,同时偏差性小的非凸log正则化方法[25]作为CTL的稀疏约束,提升CTL模型的稀疏特征提取的精确度.针对log正则化函数的非凸优化问题,本文通过使用近端凸差分算法(proximal difference of convex algorithm,PDCA)[26]对模型进行求解优化,开发出基于近端凸差分方法的多层CTL算法稀疏表示算法.

归纳而言,本文的主要贡献有以下几点:

1)为了提取深层的稀疏特征,提升稀疏特征的提取质量,将单层的CTL模型进行多层次拓展,通过对单层模型的稀疏特征进行进一步稀疏编码,实现对输入信号提取更具丰富语义与鉴别性的深层稀疏特征.

2)针对已有的基于ℓ0范数与基于ℓ1范数CTL模型提取稀疏特征存在精确度不足的缺陷,使用稀疏强、偏差小的log正则化方法作为CTL模型的稀疏约束方法,提升CTL模型稀疏特征的提取质量.

3)针对log正则化函数的非凸优化问题,使用近端凸差分算法对模型目标函数的非凸优化问题进行求解优化,开发基于近端凸差分方法的多层CTL算法.

2 相关工作

2.1 变换学习

给定一输入信号x∈Rn,变换学习通过学习一组变换基T∈Rm×n对信号进行解析,得到信号的解析特征,如图1(a)所示,其数学过程表示为Tx ≈z,其中z∈Rm为信号x对应的解析特征.具体地,变换学习模型算法可用如下函数表示:

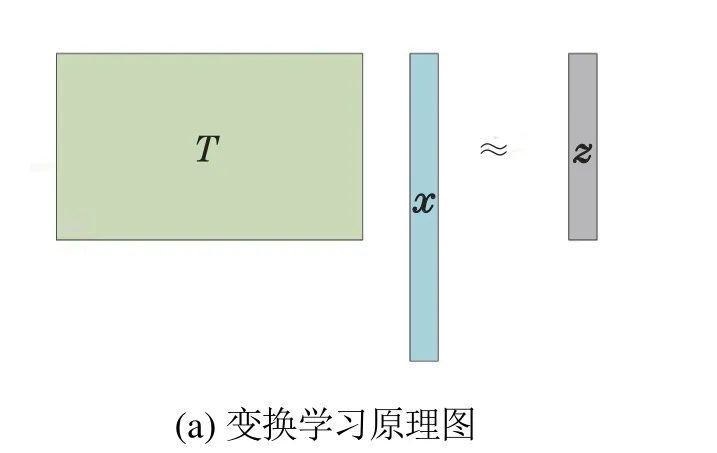
图1 变换学习与字典学习Fig.1 Transform learning and dictionary learning

与传统的字典学习算法将信号表示为字典D与其对应的权重向量或矩阵的线性组合x ≈Dz不同,如图1(b)所示,变换学习使用变换基组直接对信号进行解析得到信号的解析特征,并且在解析过程中,所有的变换基都以均等的权重和使用率参与信号的解析变换过程.因此变换学习具有更灵活丰富的表示能力.此外,在稀疏编码方面,变换学习的稀疏正则化只需通过对解析特征进行一次简单的阈值操作来求解得到信号的稀疏特征,是一种更高效的稀疏表示算法.

虽然变换学习相对于字典学习是一种更为高效的稀疏表示模型,但是它与字典学习都属于基于块的传统稀疏表示模型,如文章前言所论述,传统的变换学习模型与字典学习模型也都存在稀疏编码冗余、忽视信号的整体性、丢失特征间的关联性等问题,因此对变换学习模型的开发与应用也受到了这些模型缺陷的限制.

2.2 卷积变换学习

卷积变换学习将卷积神经网络的卷积特征提取操作引入了变换学习,如图2所示,通过学习具有平移不变性的卷积核组(卷积变换基组)直接对原始信号进行卷积提取特征,克服了第2.1小节所述传统基于块的变换学习算法的缺陷,卷积变换学习模型算法可由如下函数表示:

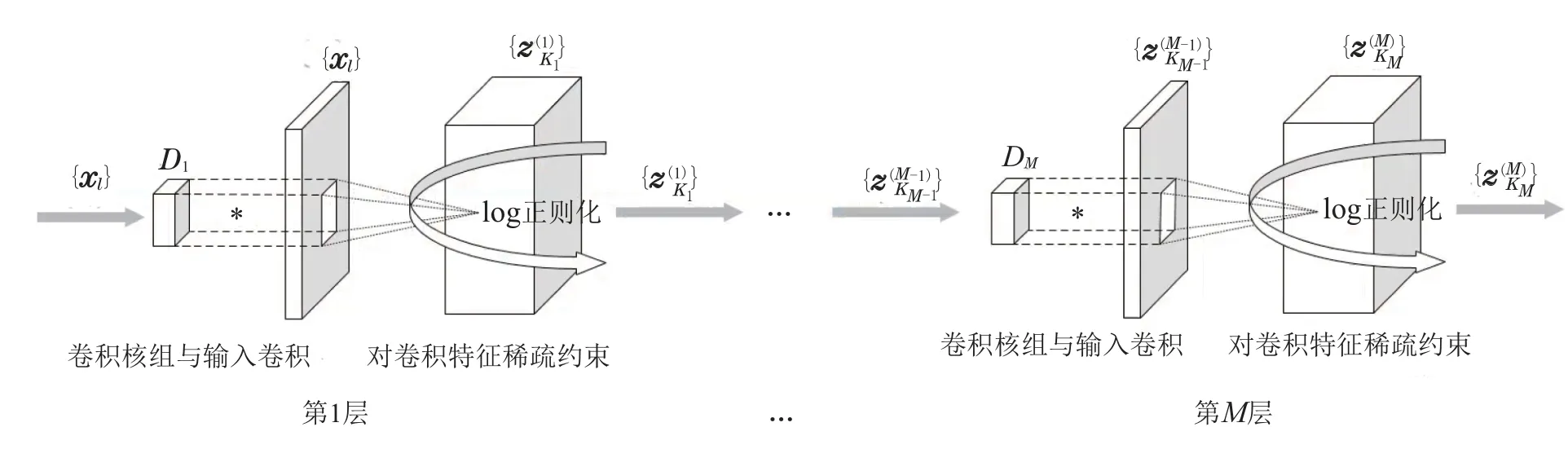
图2 多层卷积变换学习模型Fig.2 Multi-layer convolutional transformation learning model

其中:{xl∈CN,l=1,···,L}为一组包含L个输入信号的数据集,D:=[d1···dK]为由K个卷积核{dk∈CR,k=1,···,K}组成的卷积核组,每个卷积核都作用于所有输入数据进行卷积特征提取,即每个输入信号都产生相应的K个特征,{zl,k∈CN,l=1,···,L,k=1,···,K}为稀疏特征集合;Jz(z)为稀疏正则化函数;JD(D)为卷积核组的多样性正则化函数.

CTL通过学习卷积核组直接从原始信号提取特征的方式与CNN一致,可以将其视为一个通过无监督学习的单层结构CNN特征提取模型,因此,与深度神经网络相比,CTL 具有如下优势: 1)在模型学习方面,CTL 通过无监督的方式从数据的特征与内部结构学习卷积核组,在模型的学习过程中不依赖于数据的标签,而深度神经网络训练时需要大量的标签数据反向传播学习神经元,导致了当处理数据标签稀少或者没有标签时深度神经网络的应用受限;2)在数据特征提取方面,与CNN相比,CTL可以通过对卷积核组实施正则化约束的方式约束卷积核的多样性,从而减小特征提取的重复冗余,提升模型提取数据特征的丰富性.

3 基于近端凸差分方法的多层卷变换学习算法

本文通过搭建具有多层稀疏结构的卷积变换学习特征提取框架,并使用稀疏度强,同时偏差性小的非凸log正则化函数作为模型的稀疏约束,提出了一种基于log正则化稀疏约束的多层卷积变换学习模型(多层CTL-log),如图2所示.首先使用log正则化稀疏约束提升模型提取稀疏特征的精确性,其次,通过构建多层稀疏结构提取更具鉴别性与丰富语义的稀疏特征.最后,采用近端凸差分方法优化求解log正则化函数的非凸非光滑优化问题,开发基于近端凸差分方法的多层卷变换学习算法.

3.1 基于log正则化的多层卷积变换学习模型

上式中,Jz(z)是log稀疏正则化函数,其中参数λ是稀疏系数;α为log函数常系数,通过调整稀疏系数λ平衡稀疏正则化项与近似误差项之间的大小关系;δζ(D)是一个关于到紧集ζ投影的指示函数,通过到这个集合的投影来对卷积核组施加正交性约束[17].

3.2 近端凸差分方法优化求解

因为log正则化函数具有非凸性和非光滑性,所以对模型目标函数的求解也是一个非凸非光滑的优化问题.本小节通过使用近端凸差分分解算法[23]对模型进行分层求解.PDCA的思想首先通过凸差分分解方法(DCA)将优化函数中的非凸部分分解为凸函数的组合,将非凸非光滑优化问题转换为凸非光滑的优化问题,继而使用近端梯度下降法继续求解,达到对原始非凸非光滑优化问题的优化求解.

如前文所述,在多层卷积变换学习模型中,每一层得到的稀疏特征即为下一层的输入,整个模型目标函数的优化问题可以分解为多个单层的逐层优化问题,即

每一层的优化问题都是一个非凸非光滑优化问题,因此使用PDCA对模型每一层的目标函数Fm进行逐层优化.如式(8)所示,目标函数的优化包含了两个变量的求解,采用交替更新的策略,即交替固定一个变量,更新另一个变量的方式,对目标函数进行迭代优化,从而将式(8)的优化转换为式(9)与式(10)的交替迭代优化.

3.2.1 变量的更新

3.2.2 变量的更新

3.2.3 模型整体优化训练步骤

综上小节所述,基于log稀疏约束的多层卷积变换学习模型训练优化的算法过程具体步骤如表1所示.

表1 基于log正则化的多层卷积变换学习算法Table 1 Mutil-layer convolutional transform learning based on log regularizer algorithm

算法的计算复杂度主要取决于输入信号维度N与个数L、卷积核维度R与个数K.在算法的每次迭代中,更新稀疏特征的复杂度主要由d ∗x决定,即O(RKNL);更新卷积核组的复杂度主要由(d∗x)H∗x决定,即O(RKN2L).所以,算法每次迭代的主要复杂度为O(RKN2L).

4 实验分析

本节对本文提出的算法进行实验分析.首先,在第4.1节介绍实验所使用的公开数据集的详细信息,然后,在第4.2节实验设置介绍实验的流程、对比方法，以及评估指标,最后,在第4.3节呈现实验数据并对结果进行分析讨论.

4.1 实验数据集

为了验证本文所提算法的有效性,笔者在YALE[27],Extended Yale B[28]和AR-Face[29]3 个公开人脸数据集上进行了实验,数据集的具体信息及其处理与划分方法如下:

1)YALE数据集: YALE人脸数据集包含15个人,每个人在不同表情、姿态和光照下的11张人脸图像,共165张图片,每张图片原始大小为64×64像素.实验中,将图片裁剪缩小为32×32像素,首先,打乱所有图片,随机划分70%作为训练集,30%作为测试集,作为一组数据划分.此外,在每个人的11张图像中随机选择p张划分到训练集,剩下的11-p张划分为测试集,即训练集的图像数为15p张,测试集的图像数为15(11-p)张,作为一组YALE-p数据划分,通过此规则,生成新的YALE-2,···,YALE-8共7组数据.

2)E-YALE-B 数据集: Extended Yale B 数据集包含38个人,每人包含64张在不同光照情况下拍摄的人脸图像,共有2432张图像,去除其在官方采样过程被损坏的18张图像,每张图像被裁剪为192×168像素.实验中,将图片裁剪缩小为48×42像素,并打乱所有图片,随机划分70%作为训练集,30%作为测试集.

3)AR-Face数据集: AR-Face 数据库包含4000 多张人脸图像,来自126个不同的对象(70名男性和56名女性)在不同的面部表情、照明和遮挡(太阳眼镜和围巾)条件下拍摄的正面图像.实验中,随机选择其中100名对象(50名男性和50名女性),每人26张图像,共2600张图像进行实验,每张图像裁剪为540像素(27×20),并随机选择2000张图像作为训练集,其余600张图像作为测试集.

4.2 实验设置

为了验证基于log正则化卷积变换学习相较于已有基于ℓ0范数卷积变换学习[16–17]与基于ℓ1范数卷积变换学习[15]对于提取稀疏特征质量的提升,以及多层CTL-log特征提取相较于单层CTL-log的有效性,本文对于在以上数据集的实验进行了以下设置:

1)首先进行单层的CTL实验对比,在相同的模型结构下比较CTL-log,CTL-ℓ0,CTL-ℓ1的特征提取效果,验证log 正则化对于提升CTL 模型稀疏特征提取的效果;然后将单层CTL-log 拓展为双层,验证双层CTL-log相对于单层的效果.

2)实验数据集划分为训练集和测试集,训练集用于训练CTL模型的卷积核组完成CTL模型的训练,并提取训练集稀疏特征;再通过训练完成的CTL模型提取测试集的稀疏特征.

3)实验的评估指标为分类精度,将训练集的稀疏特征输入分类器进行训练学习,再输入测试集稀疏特征进行分类测试,从分类精度高低体现模型提取的稀疏特征质量优劣,即模型稀疏特征提取效果的好坏.使用的分类器为支持向量机(support vector machine,SVM).

4.3 实验结果

如上一小节实验设置所述,本小节首先进行单层实验不同稀疏约束方法的对比,然后进行单层模型与双层模型的对比,验证多层模型的有效性.

4.3.1 单层对比

如上一节实验设置所述,此小节首先在单层模型结构下,对比不同的稀疏约束下CTL模型(CTL-log,CTL-ℓ0,CTL-ℓ1)的特征提取效果.为了保证实验对比合理公平,3种CTL模型除了稀疏约束项以外,模型的其它结构均保持一致.卷积核数K=5,卷积核尺寸R=5×5,即卷积核规模为5×5×5.

第3.2.3节中算法表的输入参数λ,ηd,ηz设置如下:在数据集YALE,YALE-2∼YALE-8 的实验中,梯度步长ηd=4e-13,ηz=3e-2,稀疏参数λ的最终寻优区间为(1e-5,3e-4);在数据集AR-Face的实验中,梯度步长ηd=5e-14,ηz=8e-2,稀疏参数λ的最终寻优区间为(0.05,0.2);在数据集E-YALE-B的实验中,梯度步长ηd=4e-12,ηz=6e-2,稀疏参数λ的最终寻优区间为(0.01,0.02).

实验中,通过改变模型的稀疏约束项系数调整模型进行多次实验,分别得到模型在各个实验数据集下的最优分类结果进行比较,实验结果如表2所示.

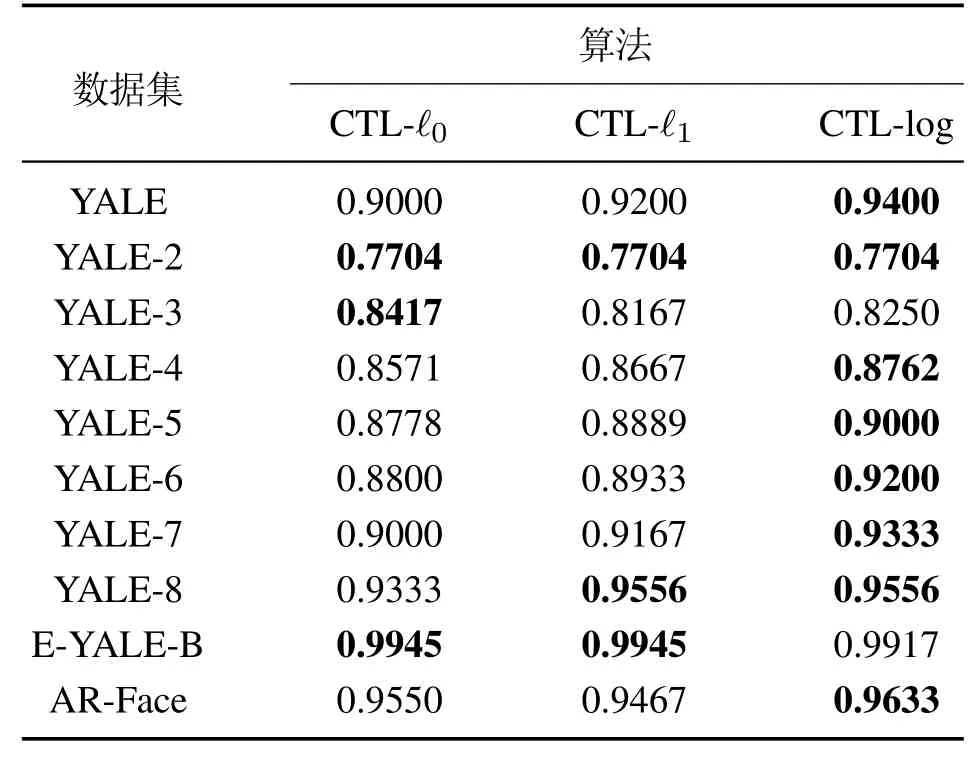
表2 单层提取特征分类结果Table 2 Classification results of single layer extraction features

根据表2实验结果显示,在所有10项数据集的分类对比实验中,CTL-log在其中8项上取得了最高或并列最高的分类准确率,表明了对于输入信号稀疏特征的提取,CTL-log的效果显然优于CTL-ℓ0与CTL-ℓ1,验证了与已有的CTL-ℓ0与CTL-ℓ1相比,引入了具有误差小且稀疏性强的log稀疏正则化的CTL-log模型具有从输入信号数据提取更高质量稀疏特征的能力.突出使用log正则化函数作为CTL模型的稀疏约束的优势.

在运行时间方面,以YALE数据集的实验为例进行分析,在实验中CTL-ℓ0,CTL-ℓ1与CTL-log在相同的迭代次数条件下的运行时间分别为110 s,82 s,87 s,CTL-ℓ1与CTL-log 的运行时间明显快于CTL-ℓ0,而CTL-log 相比于CTL-ℓ1要略微慢一些,这是因为相比于CTL-ℓ1,CTL-log在每次迭代中都要进行一次凸差分(difference of convex,DC)分解.

4.3.2 双层拓展

本小节笔者将上一小节在稀疏特征提取效果的优势得到充分验证的CTL-log拓展为双层: 将单层稀疏编码得到稀疏特征进一步进行深一层稀疏编码,在保持上一小节的单层CTL-log模型结构不变的条件下,将其作为双层CTL-log的首层,进行相同的实验策略,对比在第2层不同的卷积核组规模下(3×3×3,5×5×5,7×7×7与9×9×9)稀疏特征的提取效果,寻找确定模型第2层的最佳结构,并与单层结构CTLlog对比,验证双层CTL-log稀疏编码得到的稀疏特征质量相比于单层的提升效果.其中,第3.2.3节中算法表的最终输入参数在第1层的设置与第4.3.1节保持一致,第2层的参数设置具体如下: 在数据集YALE,YALE-2∼YALE-8的实验中,梯度步长ηd=6e-18,ηz=1.7e-2,稀疏参数λ的最终寻优区间为(5e-6,3e-5);在数据集AR-Face 的实验中,梯度步长ηd=4e-12,ηz=5e-2,稀疏参数λ的最终寻优区间为(5e-3,1e-2);在数据集E-YALE-B的实验中,梯度步长ηd=3e-11,ηz=3e-2,稀疏参数λ的最终寻优区间为(0.01,0.02).实验结果如表3所示.

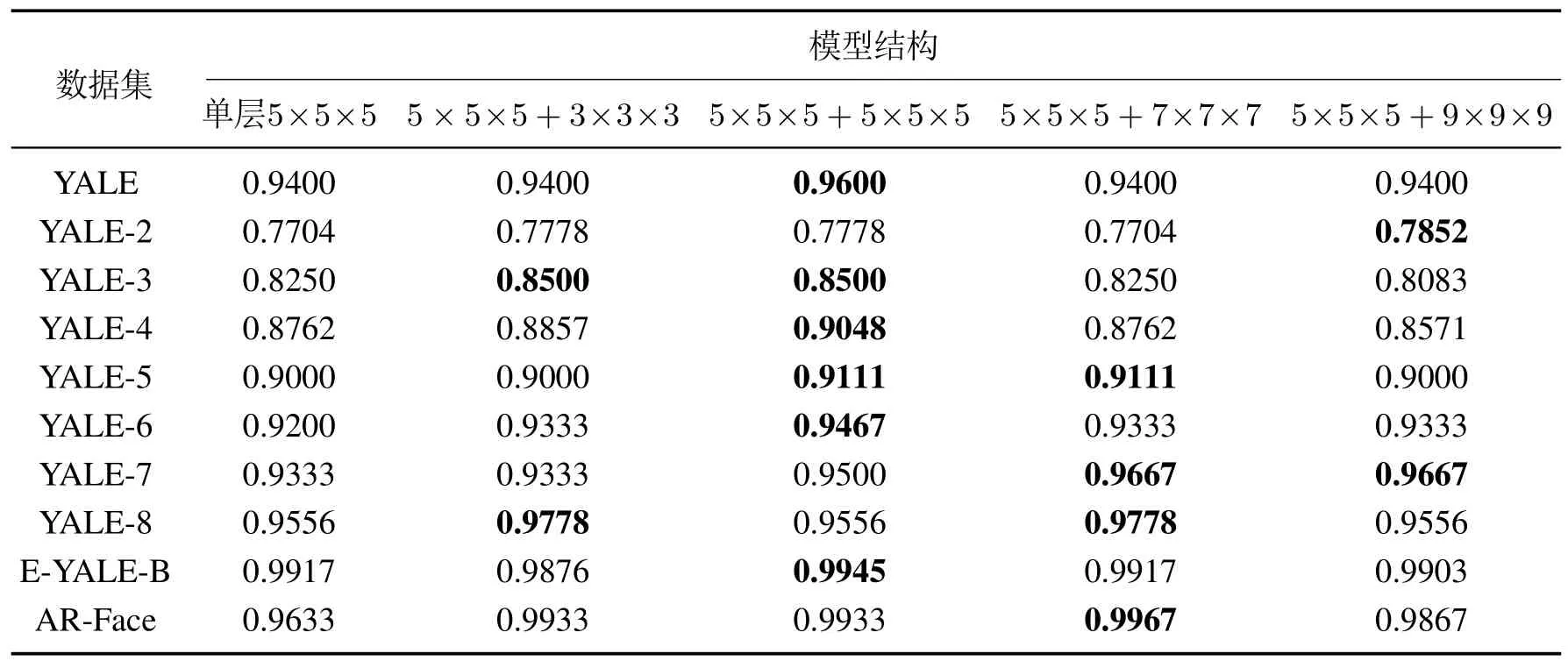
表3 双层拓展实验结果_Table 3 Experimental results of two-layer expansion of CTL-log

表3实验结果表明,在单层结构与双层结构的方面,在10项数据集的实验结果对比中,所有最优的结果(包含并列最优)全部在双层CTL-log中产生,表明通过对单层CTL-log稀疏编码得到的稀疏特征的进一步稀疏编码提升了稀疏特征的提取质量;在不同双层结构的内部对比方面,在第2层的卷积核组规模分别为3×3×3×3,5×5×5,7×7×7,9×9×9这4种不同结构下的双层CTL-log在10项数据集实验中得到最优结果的次数分别为2,6,4,2,从取得最优结果次数的角度看,第2层卷积核组规模为5×5×5时双层CTL-log的效果最好.

此外,通过计算10项实验结果准确率的整体平均值,从平均准确率角度对比各模型结构的效果,如图3所示,同样可以看出双层CTL-log的平均准确率也都高于单层CTL-log,并且双层CTL-log卷积核组规模为5×5×5+5×5×5时平均准确率与最优次数均为最高,说明通过对CTL-log的双层拓展,提取得到了输入信号更具鉴别性与丰富语义的稀疏特征,提升了模型的稀疏特征提取质量,且当第2 层卷积核规模为5×5×5时提升效果最好.

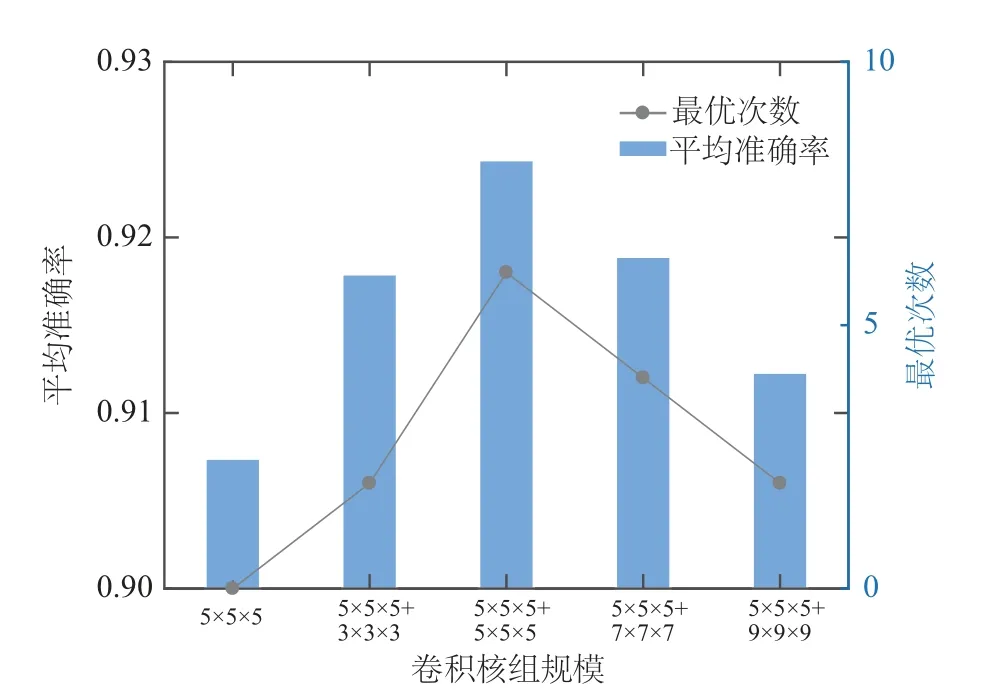
图3 不同CTL结构的分类平均准确率与最优次数对比Fig.3 Comparison of average accuracy and optimal times of different CTL structures

综上分析,可以得出在保持第1层结构不变的情况下,双层CTL-log 第2 层卷积核组规模设置为5×5×5时,模型对于稀疏特征的提取整体效果是最好的,因此将第2 层的卷积核规模设定为5×5×5.CTL-ℓ0,CTL-ℓ1,CTL-log与双层CTL-log的最终对比如表4所示.

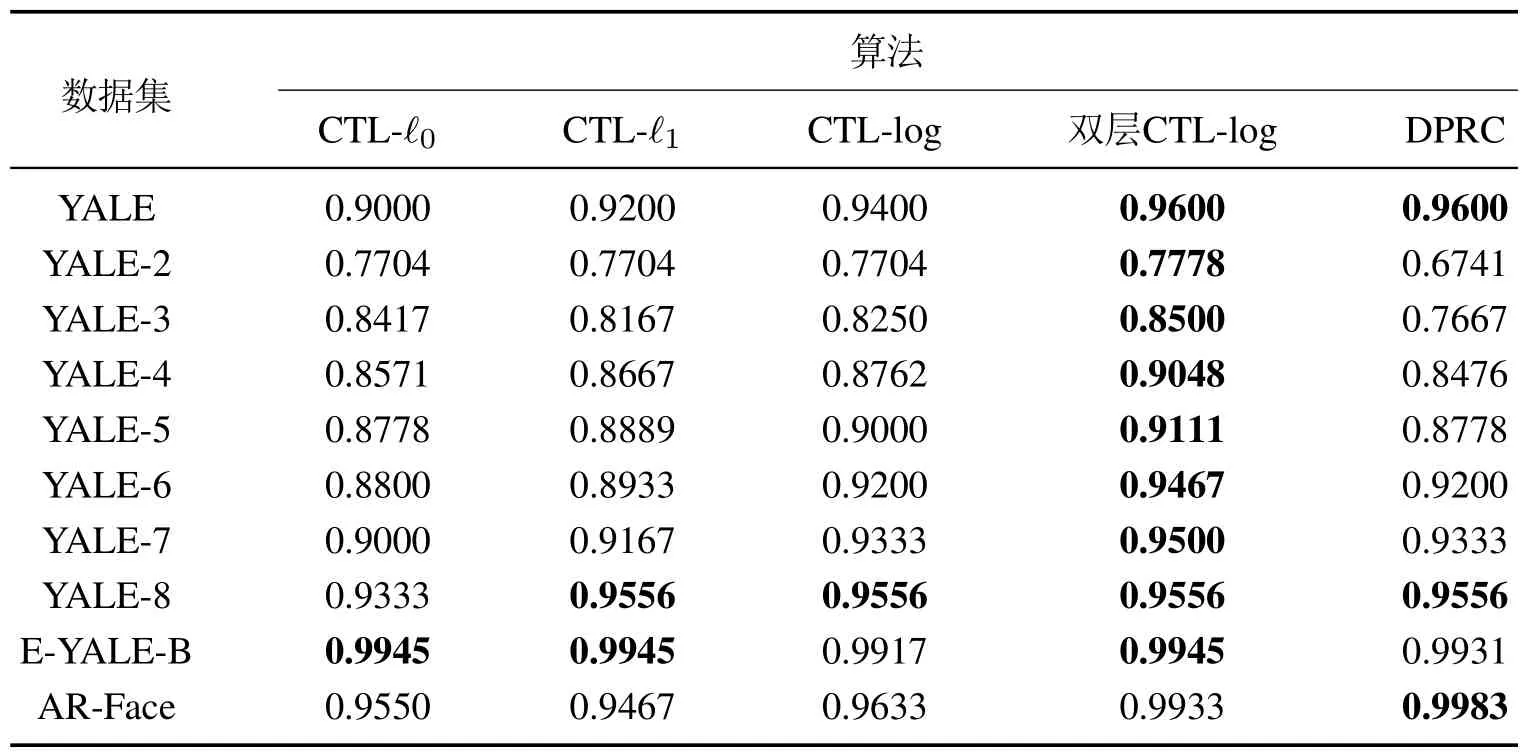
表4 不同CTL模型及DPRC分类结果对比Table 4 Comparison of classification results of different CTL models and DPRC algorithm

如前文所述,与已有的CTL-ℓ0,CTL-ℓ1相比,引入log正则化函数稀疏约束的CTL-log能够提取得到具有更高精确度,质量更高的稀疏特征,并且通过将CTL-log拓展为双层CTL-log对输入信号进一步的稀疏编码提取了输入信号更具鉴别性与丰富语义的深层次稀疏特征,进而提升了模型提取稀疏特征的质量.

此外,为了验证本文提出算法当下的有效性,除了与CTL模型的实验对比外,还与当下最新的人脸识别算法之一,基于判别投影和表征的分类(discriminative projection and representation-based classification,DPRC)[30]算法进行对比,实验结果如表4所示.从DPRC与双层CTL-log的实验结果对比可以看出,在10项分类数据集分类结果的对比中,双层CTL-log除了在YALE,YALE-8与DPRC 持平,AR-Face略低于DPRC外,在其余的7项结果都要明显优于DPRC,表明了与DPRC算法相比,本文的双层CTL-log算法具有更好人脸识别分类效果,验证了本文提出算法在当下的有效性.

5 结论

针对已有的卷积变换学习模型存在的问题,本文提出了基于近端凸差分方法的多层卷变换学习算法,该算法通过对单层卷积变换学习模型的稀疏特征进行进一步的稀疏编码,提取输入信号更具丰富语义与鉴别性的深层稀疏特征,并且使用稀疏度强,偏差性小的非凸log正则化函数作为卷积变换学习模型的稀疏约束方法,通过使用近端凸差分算法对模型的非凸优化问题进行优化求解,构建基于log正则化函数稀疏约束的多层卷积变换学习特征提取框架.

在公开的人脸图像数据集的特征提取实验结果表明,本文提出的多层log稀疏约束卷积变换学习模型的人脸图像稀疏特征提取质量优于已有的基于ℓ0范数与基于ℓ1范数的卷积变化学习算法,并且基于log正则化函数的多层卷积变换学习通过层次的拓展有效提升了稀疏特征的提取质量,取得了更高的分类精度.

在未来的工作中,笔者将对提出的算法进行进一步深度层次的开发,并拓展应用到心电信号数据的分类.