融通算理算法，构建知识体系——以“小数乘小数”的教学为例

江苏省常州市新北区春江中心小学 张晓锋 姚灵娣

《义务教育数学课程标准（2022 年版）》指出，数的运算重点在于理解算理、掌握算法，数与运算之间有密切的关联……经历算理和算法的探索过程，理解算理，掌握算法。初步体会数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识；感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。

“小数乘小数”是苏教版数学五年级上册“小数乘法和除法”单元的教学内容。整数乘法和小数乘整数的算理算法与积的变化规律等是学生学习“小数乘小数”的学习基础。笔者以为，本课教学应创设真实情境，触发学生学习的“兴奋点”，引导学生自主迁移，结合图形，从计数单位的角度理解小数乘小数的算理，探索并掌握小数乘小数的算法，且快速、准确地为积的小数点“定位”，发展学生的数感与推理意识。

片段一：创设真实情境，点燃学习热情

课件呈现老师家的户型图（图中标注了主卧长4.2米、宽3.5 米，次卧长3.8 米、宽3.2 米，阳台长3.2 米、宽1.15 米，卫生间长3 米、宽2.8 米）。

师：同学们，这是老师家的户型图，这套房子的面积是98.6 平方米。你们从图中看到了哪些数学信息？

学生回答。

师：仔细观察老师家的户型图，你们能提出哪些数学问题？

生1：我想知道阳台的面积有多大。

生2：我想知道次卧的面积有多大。

生3：我想知道主卧比次卧大多少。

生4：我想知道这套房子的总价。

……

师：同学们想知道的挺多！这些问题都可以通过乘法计算得出答案。请大家先算出卫生间的面积，再互相说说整数乘小数的计算方法。

师：我们算出卫生间的面积是8.4 平方米。你们能列式计算次卧的面积吗？请每个同学尝试列竖式计算。（板书3.8×3.2）

……

【思考】情境认知理论认为，基于现实世界的真实情境是学习者学习的基本条件，任何脱离特定情境或场合的知识都是毫无意义的。学生对生活中的一些真实问题最感兴趣。以老师家的户型图作为学习素材导入，能激发学生的好奇心与解决问题的内在需求，也为学生积极提出不同问题、列出不同的乘法算式提供了条件。比较契合数学眼光的主要表现之一为“能够在实际情境中发现和提出有意义的数学问题，进行数学探究；逐步养成从数学角度观察现实世界的意识与习惯，发展好奇心、想象力和创新意识”。创设真情境、解决真问题、引领真学习，有利于实现学习与现实的有意义联结。

片段二：增强估算意识，丰富学生数感

师：同学们，3.8×3.2 的积是多少？我们先估算一下！

生1：我把3.8×3.2 当成4×3 估算，积大约是12。

生2：我把3.8×3.2 当成3.8×3 估算，积大约是11.4。

生3：我把3.8×3.2 当成4×4 估算，积大约是16，不过积一定小于16，因为这是大估。

生4：我把3.8×3.2 当成3×3 估算，大约是9，我用的是小估！

师：大家的估算方法多样，估计积在9 到16 之间。大部分同学估算的积约为12。我们先把这个估算结果记录下来，等会儿将其与竖式计算结果比对。

……

师：同学们，下面三个竖式（见图1）计算对吗？先判断，然后把不正确的改正过来。

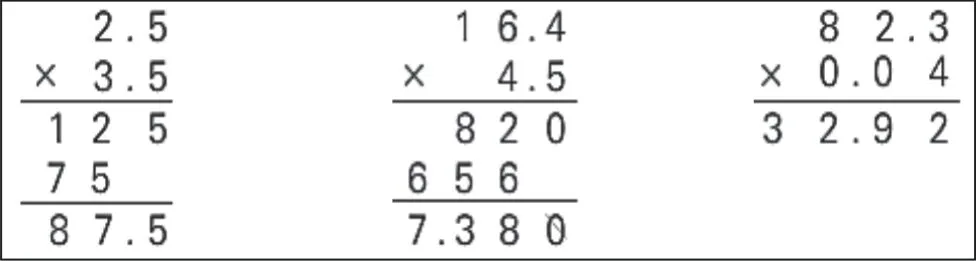
图1

师：谁能很快判断出这三道题的对错？

生1：第一个竖式是2.5×3.5，我大估成3×4 口算，积是12，87.5 太大了！第二个竖式是16.4×4.5，我小估成16×4 口算，积是64，7.38 太小了。

师：大家同意他的判断方法吗？通过估算可以很快知道两个数相乘的积的大致范围，如果相差太大那就错了。第三个竖式哪里错了？

生2：我认为第三个竖式的得数也可以通过估算判断，把它估成80×0.04，积是3.2，32.92 太大！还可以把82.3 大估成100,100×0.04=4，仍然比32.92 小得多！

生3：我有不同的判断方法！我是从积的小数位数看的。请看，第一个竖式的积应该是两位小数，而这里是一位小数；第二个竖式的积应该是两位小数，而这里是三位小数；第三个竖式的积应该是三位小数，而这里是两位小数。所以三道题都算错了！

师：善于思考，方法灵活！

师：估算的功能的确强大！判断一个乘法竖式的积是否正确，既可以通过估算判断，也可以通过确定积是几位小数判断。大家在日常计算中，要养成估算的好习惯，完成计算后再检查、反思，给自己的计算加个保险！

【思考】估算能力是运算能力中一项必备能力，有助于发展学生的内省智能。新课标指出，估算教学要借助真实情境，引导学生在选择合适单位估算的基础上，感悟选择合适的方法估算的重要性，提高解决问题的能力，发展初步的应用意识。教师在学生尝试计算前先引导学生估算，唤醒他们先估再算的意识，最后将估算值与竖式计算结果对照，发展学生的内省智能。借助教材中的三个有错的竖式组织学生判断，促进思考，引导学生从估算的角度与确定小数点位置的角度辨错。这样能拓宽辨析视角，强化估算能力。抓实关键“一点”，学生计算小数乘法中的“点点”技能得以强化与巩固，从不同视角解决同一问题的经验不断丰富，运算素养也得以逐步提升。

片段三：发展推理意识，滋养算“术”智慧

师：请同学们自主尝试，列竖式计算3.8×3.2 的积，算好后在小组内交流自己的算法。

学生列竖式计算，教师巡视指导。

全班交流，教师投影两个学生列的竖式（略），积分别是12.16 和121.6。

教师让生判断哪个积正确，学生联系前面估算的积约是12，判定得数121.6 错误，12.16 正确。

师：谁愿意说说自己的计算过程？关键要讲清楚你是怎么想的。

生1：我先把3.8×3.2 看成整数乘法计算，就是看成38×32 来计算，积是1216。因为3.8×10 等于38，3.2×10 等于32，两个乘数都乘了10，所以最后要根据积的变化规律，把两个整数相乘的积1216 除以100，就能得出正确的积12.16！（见图2）

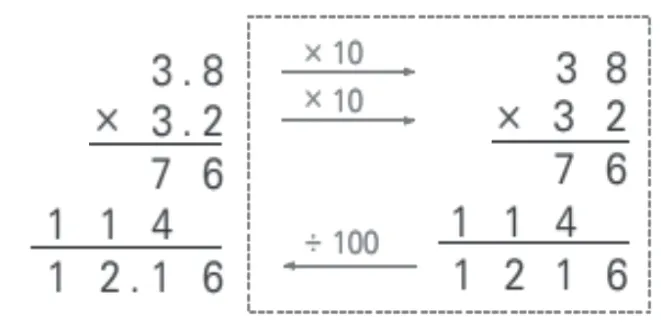
图2

师：我们可以应用积的变化规律，将一位小数乘一位小数转化为整数乘整数，最后在积的相应位置点上小数点。怎样确定积的小数点位置？

生1：把1216÷100，就是把小数点向左移动两位，得到12.16。

师：同学们真棒，善于联系、乐于思考。小明想和大家分享他的不一样的计算过程。

师：谁看懂了他的算式？说说自己的理解。

生2：他是从计数单位的角度来计算的，38 个0.1乘32 个0.1，0.1×0.1 表示新的计数单位，1216 表示新的计数单位的个数。

师：想一想，0.1×0.1 能得到哪个新的计数单位？很多人猜是0.01，你们的数感真好，确实是0.01。让我们通过动画了解0.01 的“出生历程”。

学生观看动画了解0.01 的产生过程（见图3）。先把一个正方形横着等分10 份，1 份是，即0.1；再竖着等分10 份，1 份也是，即0.1。学生看明白了将计数单位细分的过程，即将一个正方形分了再分，等分成100份，每份为0.01。

图3

师：小明从计数单位的角度理解小数乘法计算的道理。大家能理解吗？

生3：3.8 的计数单位是0.1，它有38 个0.1；3.2 的计数单位是0.1，它有32 个0.1。可以把3.8×3.2 看成38×0.1×32×0.1。先算0.1×0.1，得到的0.01 是一个新的计数单位，而38×32 得到的是新的计数单位的个数，是1216。1216 个0.01 就是12.16。

师：思路清晰，表达有序。大家能将列竖式计算与从计数单位的角度计算联系起来吗？先独立思考，再在小组内交流。

（教师组织全班交流）

生4：请看竖式（见图2），3.8×10 得到38，相当于38 个0.1，3.2×10 得到32，相当于32 个0.1。38×32 的积是1216，表示1216 个0.01，即12.16。

师：妙！数学知识是有联系的，数学是讲道理的。将不同方法之间的“隔断墙”打通，就会发现其中的共通之处！请大家列竖式计算老师家的阳台面积，完成的同学还可以从计数单位的角度用递等式计算。

生计算并交流。

生5：我先算115×32=3680，从竖式可以看出1.15乘100 等于115，3.2 乘10 等于32，相当于把积乘1000，所以要将3680 除以1000，也就是把小数点向左移动三位，得到积是3.680，最后把小数部分末尾的0 划掉，所以积是3.68。

师：他运用积的变化规律快速准确地算出了3.2×1.15 的积。也有同学从细分计数单位的角度求出了积。请看！（投影学生资源）

师：大家都很善于学习！既能运用积的变化规律计算小数乘法，还能从计数单位的角度计算并理解其中的道理，了不起！我们一起回顾3.8×3.2 和1.15×3.2 两个竖式，说说把它们看成整数乘法算出积后，怎样准确、快速地确定积的小数点位置？有什么诀窍？

生6：两个乘数中一共有几位小数，积就是几位小数。

生7：积是几位小数，就从整数乘法得出的积的末尾往左数出几位，再点上小数点，如果小数部分末尾有0，要把0 划去。

师：同学们真善于发现和归纳。你们能结合自己的发现，快速填写下面的表格吗？

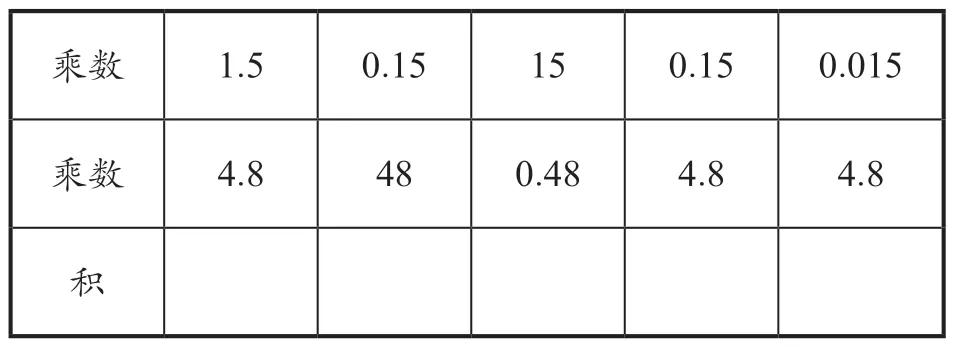
乘数1.5 0.15 15 0.15 0.015乘数4.8 48 0.48 4.8 4.8积

师：请同学们先仔细观察表中的数据，说说有什么发现。

生8：这些数据都与15 和48 有关，都是15 个计数单位乘48 个计数单位。

师：真善于观察！同学们，只要计算一个乘法竖式的积，就能很快推算出这5 个积。哪个乘法竖式这么重要？

生9：我认为是15×48。因为15×48=720，而第一列1.5×4.8 的积是两位小数，所以只要将720 的小数点向左移动两位，得到7.2。剩下四列都依此类推，如0.15×4.8=0.72，0.015×4.8=0.072，等等。

【思考】学起于思，思深于联。算理与算法是运算能力的两翼。新课标增加了“感悟运算的一致性，发展运算能力和推理意识”这一要求，让学生感悟“多少个计数单位”的表达是算理和算法的基础，促进学生对核心概念“计数单位的‘累加’”的理解。教师先鼓励学生独立尝试列竖式计算3.8×3.2，促进学生迁移学习，学生自觉调用前一课的学习经验，利用积的变化规律正确计算，发展推理意识。设计中增加一个环节，引导学生从计数单位的角度计算，旨在落实新课标提出的运算一致性要求，同时将应用积的变化规律计算和从计数单位的角度计算相互勾连，顺畅衔接，帮助学生明晰算理，便于学生进一步感悟计数单位在运算中的作用及运算的一致性。此外，以画图、动画演示等方式帮助学生理解0.1×0.1 得到新的计数单位0.01，直观形象。整个学习过程有效地融通算理、算法，有助于学生自主建构知识体系。