借助几何直观培养小学生数学核心素养

江苏省南京师范大学附属中学新城小学北校区 张勇成

江苏省南京致远外国语小学 刘 媛

一、问题提出：图形直观的数学意义

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）指出，小学阶段核心素养主要表现为数感、量感、符号意识、运算能力、几何直观、空间观念、推理意识、数据意识、模型意识、应用意识、创新意识。几何直观有助于把握问题的本质，明晰思维的路径。曹培英在《跨越断层，走出误区》一书中也介绍：一方面，直观是数学抽象的基础与数学认知的有力支撑；另一方面，直观又是数学理解，乃至数学抽象的重要内涵与数学本质认识的深化。联系小学生的发展特点，由于生理与心理上的日趋成熟，他们的求知欲发展得很快，抽象思维能力也在不断发展，导致他们更关注知识的形成过程而不仅仅是结果。此时，如果进一步落实学生几何直观能力的培养，不仅可以帮助学生将抽象知识变得直观可视，更能让学生将原本错综复杂的知识进行关联，从而探寻知识间的内在联系。

二、教学思考：几何直观的应用价值

（一）化复杂为简单，推理数学规律

在新课标中，几何直观主要是指利用图表描述和分析问题的意识与习惯。这也为一线教师的课堂教学指明了方向。

比如，苏教版数学四年级下册“三位数乘两位数”单元中有这样的思考题：用0，1，2，3，4这五个数字组成一个两位数和一个三位数，要使乘积最大，应是哪两个数？要使乘积最小呢？解决这个问题有两个关键：一是要使乘积最大，大数占高位；要使乘积最小，小数占高位；二是和一定，两数之差越小，乘积越大；两数之差越大，乘积越小。教学中，教师可以借助几何直观来分析数位及数量之间的关系，帮助学生形象直观地理解规律中隐藏的秘密。

【情况1】乘积最大，0放在三位数的个位上

联系图示可知（如图1），0和任何数相乘结果都为0。如果0放在三位数的个位上，依次要和两位数的个位、十位相乘，相当于损耗了个位、十位；而0放在两位数的个位上，依次要和三位数的个位、十位以及百位相乘，相当于损耗了个位、十位和百位。要使乘积最大，损耗就要尽可能小，所以0放在三位数的个位上。

【情况2】乘积最小，0放在两位数的个位上

依旧联系图示（如图2）进行上述分析。这里要使乘积最小，损耗就要尽可能大，所以0放在两位数的个位上。

图2

接着再研究其他数位上的数，学生就能够顺利解决了。

（二）将抽象变直观，实现知识迁移

借助几何直观可以建立形与数的联系，构建数学问题的直观模型。在实际课堂教学中，笔者也通过尝试发现，借助几何直观不仅能够帮助学生发现图形深层次的含义，直观理解数学，记忆某些结论，发展重要的学习能力，还能够帮助学生实现知识的迁移，建立起新旧知识之间的联系。如在苏教版数学五年级下册“和的奇偶性”一课中，笔者主要设计了以下三个环节：

【环节1】教师出示三个抽奖转盘（如图3）和游戏规则：转动转盘，若指针指着的两数相加的和是奇数，则中奖。通过调动学生生活中参加游戏中奖的经验，激起他们探究的欲望，引导他们思考：“为什么没有中奖？怎样才能中奖？”学生自然调动原有经验举例验证，继而发现，要判断两个数和的奇偶性可以直接计算个位上的数相加的和。

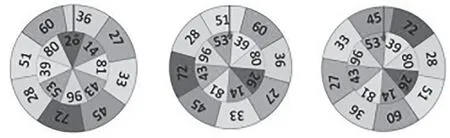
图3

【环节2】基于举例验证得出猜想正确后，教师提出“以形助数”的验证方法（如图4）：如果用1个方格表示1，2个方格就表示2，3个方格就表示3，以此类推，这里第一行表示的都是奇数，第二行表示的都是偶数，结合数的奇偶性，学生会发现：偶数对应的都是完整的正方形或长方形，奇数对应的不是完整的图形，或表示奇数的都多1格，表示偶数的都正好摆成2排。帮助学生通过图示深层次理解奇偶数及其求和后的特点，借助几何直观，为学生打开了验证规律的另一扇窗。接着，教师利用所给的材料，鼓励学生合作探究其他的验证方法，拼图验证两个不是0的自然数的和的奇偶性。学生在拼摆过程中总结出结论：偶数＋偶数＝偶数、奇数＋奇数＝偶数、偶数＋奇数＝奇数。

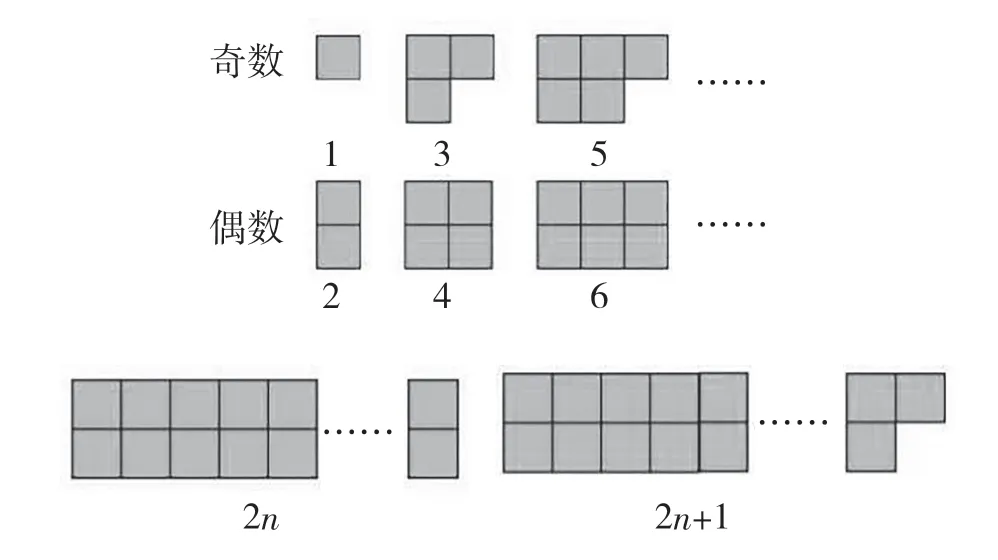
图4

【环节3】学生继续通过方格图逼近知识本质，通过分类讨论三种情况：若干个偶数相加的和是偶数；奇数个奇数连加的和是奇数；偶数个奇数连加的和是偶数。

和的奇偶性问题本身是十分抽象的，但借助方格图的直观性作为形象支撑，通过层层递进的方式一步步把两个或几个数相加的和的奇偶性规律展示出来，既渗透了数形结合、转化、化归等数学思想，又更有效地提升了学生的数学素养。

（三）由内隐到外显，掌握数学本质

比较、沟通和联想是帮助学生由内隐走向外显，探寻知识本质的基本路径。曹培英也在《跨越断层，走出误区》一书中指出，沟通同类事物内在的联系，可实现几何直观的结构意义。可见，用几何直观联结“数”与“形”之间的关系，可以充分激发学生的推理能力，提升学生的创新意识，从而帮助学生更加深刻地理解数学知识的本质，灵活运用数学思想方法。

在教学苏教版数学六年级上册“分数乘分数”一课时，笔者通过课前调查发现，不少学生已经在课前基本学会了分数乘分数的算法，那么，理解分数乘分数的算理、沟通算理和算法之间的联系便成了本节课的重中之重。在这里，笔者也设置了三个环节：

【环节1】“数”“形”结合，初探算法

先出示例题（如图5），让学生尝试列式并猜测结果，再鼓励其用学过的方法证明结论。在这个问题中，正确计算出结果并不难，但对于为什么用分子相乘的积做分子、分母相乘的积做分母，学生并不清楚。因此，教学时要让学生用自己学过的知识证明对此，多数学生用的是化成小数的做法（如图6），极个别的用了画图的方法（如图7）。此时，教师可以引导学生意识到：将“数”和“形”进行沟通，可以清晰地看到算法中隐藏的道理。

图5

图6

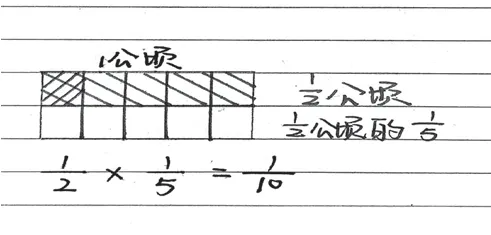
图7

【环节2】由“数”到“形”，理解算理

在学生已经能用“化成小数”和“画长方形图”两种方法证明分数乘分数的基础上，继续鼓励学生证明的结果。这时，不能化成有限小数，这就激发了学生的又一次反思——可以用画图的方法来证明。经过层层递进的环节，学生在一次又一次反思的过程中，借助几何直观的“可视性”，慢慢接近了分数乘分数的算理。

【环节3】由“形”到“数”，融通理法

教材中提供的是静态的结果图，所以笔者在学生经历了用画图的方法找出分数乘分数的结果的过程后，反其道而行，鼓励学生根据图示写出算式，再一次利用几何直观让学生沟通算理和算法之间的联系。经过前两个环节，这里学生看到的虽然是静态图，但是已经可以通过联想，化静态图为动态图（如图8）。

图8

像这样，学生在算式和几何直观中建立“数”与“形”的联系，不断经历由反思到重构的过程，将思维从几分之一乘几分之一延伸到几分之几乘几分之几，乃至分数乘整数，直观感受分数乘分数的算法，揭示分数乘分数算理的本质，逐步完成对分数乘法计算法则的整体建构。

三、实践探索：几何直观的实施路径

几何直观能告诉我们什么是可能重要、可能有意义和可接近的，并使我们在课题、概念和方法的荒漠之中免于陷入歧途之苦。培养学生的几何直观能力具有重要意义。对于如何切实培养学生的几何直观能力，笔者也尝试进行了一些思考。

（一）释意义：在直观中丰富数形经验

几何直观通过直观感知、数形结合，可以培养学生的几何直观能力。比如，在平均数问题中，借助条形图的直观性进行分析，可以抽象出“求平均数”的本质即“移多补少”；在近似数意义的理解中，也可以借助数轴，直观地感知“四舍五入”中“几十五”约等于后一个整十数的道理。

在苏教版数学五年级上册“小数的近似数”一课，有一道思考题：“有一个三位小数，精确到百分位是4.80。这个三位小数最大是多少？最小呢？”对于这一问题，多数学生采取的是“分析法”，即要想三位小数最大，千分位需要“四舍”，所以4.80不变，千分位写4，也就是三位小数最大是4.804；反之，要想三位小数最小，千分位需要“五入”，那么4.79可以通过“五入”得到4.80，这时千分位还要尽可能地小，也就是三位小数最小是4.795。但是，其中的道理如何帮助学生理解呢？可以用“数轴”来直观地分析。在数轴中（如图9），先固定4.80的位置，根据“沿着正方向（一般从左往右，以箭头指向为准）数轴上的数越来越大”，先确定近似数为4.80的三位小数的取值范围在4.79～4.81，即固定数轴中4.79和4.81的位置。接着，在两位小数的基础上继续关注千分位，缩小取值范围：根据四舍五入原则，大于4.79而小于4.80的三位小数中，4.795为近似于4.80的最小值，同理，大于4.80而小于4.81的三位小数中，4.804为最大值，从而最终确定了准确结果。

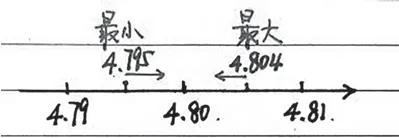
图9

这样，不仅为学生创造机会积累数形经验，用图形直观阐释小数近似值的确定方法，也在不断缩小取值范围的分析中渗透数形结合思想。

（二）理关系：在操作中助力概念理解

学生几何直观能力的培养不能只是停留在画图、看图、分析图的层面上，还要有剪、拼、折、围等操作活动，这样才能更好地把数学知识由抽象变为具体。在几何图形概念的教学中，如果能通过操作直观地进行深入观察，往往能帮助学生对几何图形建立深刻的表象体验，引发学生深度思考，从而更准确地把握几何图形的要素。

如苏教版数学四年级下册“认识三角形”一课的教学。在理解三角形特征的环节，教师提供了火柴棒、毛线、点子图和钉子板四种工具，鼓励学生通过摆一摆、拉一拉、画一画、围一围等方法做一个三角形。交流时，让学生在充分体验的基础上对三角形的概念进行提炼，总结出“三条线段”“首尾相接”“围成”等要素。最后，利用生成的资源激发学生深度思考的意识，提出“回顾做三角形的过程，你觉得有哪些注意点”这一问题，为学生提供完整的反思机会，从而为学生由深入观察到深刻体验，最终走向深度思考画上一个完整的句号。

整个环节中，不仅借操作帮助学生积累几何直观经验，也利用归纳思想对不同方法制作出的三角形特点进行要素提炼，并归纳总结出三角形的概念，使学生对三角形的理解从感性层面上升到理性层面。

（三）明数理：在形象中掌握知识本质

“‘形’缺‘数’时难入微，‘数’缺‘形’时少直观”是著名数学家华罗庚先生的名言。数形结合思想便是掌握数学本质的有力抓手，充分运用图形的直观功能，在形象中看透抽象本质，可以使学生的数学理解力逐步提升。

教学苏教版数学五年级下册“解决问题的策略——转化”一课时，笔者发现在计算的结果时，几乎所有学生都不约而同地选择了通分，甚至有学生尝试将分数逐一转化成小数后再进行加法计算。基于学情，笔者将练习题进行了调整：计算。此时，“通分”和“化小数”的方法都不方便，以此激发学生探究新策略的欲望。这样，通过“形”来解决问题就显得很重要。学生可以把正方形看作单位“1”，结合已有经验以及分数的意义，迅速领悟到其中的奥妙（如图10）：这些分数相加的和，就是单位“1”减去最后剩下部分的差，而最后的剩下部分对应的就是最小的那个加数，从而发现

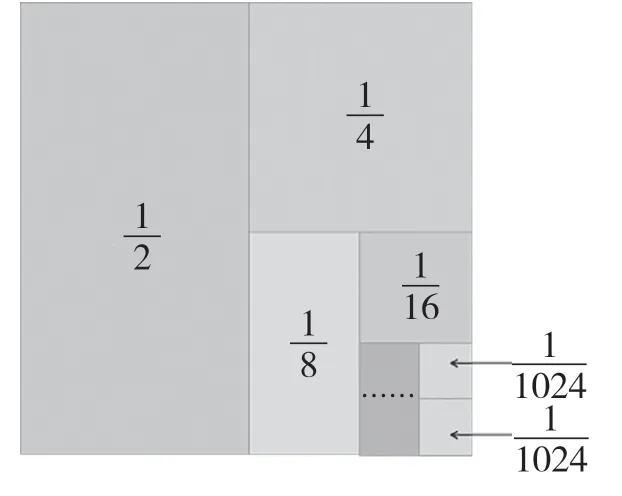
图10

探究过程中，学生通过数形结合的直观分析，不仅可以掌握数学知识的本质，更能深刻地体会到转化思想带来的无穷魅力。

（四）找方法：在简明中拓展思维空间

归纳推理也是小学阶段一种重要的数学思想，常常以特殊为起点，寻求解决问题的一般方法和规律，再反过来指导特殊问题的解决。

再以苏教版数学五年级下册“解决问题的策略——转化”为例，练习中出现了三组题：“练一练”的第2题，实质是启发学生将求一组连续自然数和的连加算式转化为可以用乘法计算的同数连加算式；“练习十六”的第5题，既可以借助“练一练”第2题的经验，转化用乘法计算的同数连加算式，也可以联系平均数的特点直接确定这九个数的平均数，旨在鼓励学生根据题目特点合理选择；而“练习十六”的第7题则以形助数，把从1开始的连续奇数相加借助直观图转化成求一个数的平方。三组题目同为数列求和问题，但各有偏重，这是“同中见异”的落脚点，但亦有“异中求同”的生长点，即都在丰富学生转化思想的经验。所以笔者也进行了大胆的尝试：将三组问题编为一组，先逐一呈现，深挖其落脚点，再合并观察比较，生发其共同处——无论是连续自然数求和，还是连续奇数相加，每组数中相邻两数的差是一定的，从而归纳出等差数列的求和一般方法。

这样，把内容放在知识体系中研究，关注前后知识的衔接，同中见异、异中求同，将学习研究的素材合理编排，这才是有效发展学生数学素养的重要保证。

正如数学家希尔伯特在《直观几何》中所描述的那样，“图形可以帮助我们发现、描述研究的问题，可以帮助我们寻求解决问题的思路，可以帮助我们理解和记忆得到的结果。”可见，只要教师留心观察、积极思考，以让学生亲身经历与数学相关的学习过程为设计理念，将几何直观作为有力抓手，就能为学生思维的发展、能力的提升添砖加瓦。