有桩自行车共享系统吞吐率的近似模型及算法

王静妍 张勇

摘要：通过探讨用户需求和骑行时间不确定的有桩自行车共享系统（docked bike-sharing system， DBSS）建立吞吐率的近似模型及算法。一个具有固定自行车数量的DBSS可视为封闭的排队网络，每个站点都是有限的M/M/1队列，由此建立了DBSS吞吐率的近似模型及其算法。该算法不仅能够计算道路上期望的自行车数量、骑行时间、车站的期望库存及停留时间，还能计算最优自行车投放量，即吞吐率最大值对应的最小的自行车投放量。同时，给出了给定用户需求、路由矩阵和车桩分配下站点自行车集聚与空缺的判断方法。将该近似算法在真实的DBSS中进行了应用。结果表明，随着自行车投放量的增加，系统吞吐率呈阶梯形递增但存在上限；自行车投放量一旦超过最优数量将产生闲置，并且自行车集聚与空缺站点分布也将固定。

关键词：有桩自行车共享系统；运营效率；封闭排队网络；吞吐率；空满桩站点；自行车投放量

中图分类号：U491   文献标志码：A   文章编号：1002-4026（2023）06-0074-12

An approximate model and algorithm for throughput rate of

a docked bike-sharing system

WANG Jingyan， ZHANG Yong*

（School of Rail Transportation， Soochow University， Suzhou 215131， China）

Abstract∶In this paper， an approximate model and algorithm for the throughput rate are established by studying a docked bike-sharing system （DBSS） using stochastic user demands， routing matrix， and cycling times. A DBSS with a fixed number of bikes can be considered a closed queuing network with a buffered M/M/1 queue at each station， thus establishing an approximate model and algorithm for the throughput rate of DBSS. This algorithm can calculate the average number of bikes on roads and at stations. Moreover， it can estimate the average cycling time on roads and bike dwell time at stations and further determine the optimal number of bikes achieving the maximum throughput rate in the DBSS. Additionally， this paper proposes a method to determine whether a station is a bike surplus station or a bike deficient station under given user demands， routing matrix， cycling time matrix， and dock allocation. Finally， the approximate algorithm is verified in a real-world DBSS. The results show that the throughput rate of the DBSS increases in a step-wise manner with the increasing bike input under an superior limit. When the number of bike inputs exceeds the optimal quantity， there will be idle bikes， and the spatial distribution of bike surplus stations and bike deficient stations will remain unchanged.

Key words∶docked bike-sharing system; operational efficiency; closed queuing network;system throughput rate; bike surplus and deficient stations; bike input

有樁自行车共享系统（docked bike-sharing system，DBSS）是基于固定站点提供借还自行车服务的服务系统［1］。近年来在全球得到了广泛应用，截至2022年12月，全球建设了1 900多个有桩自行车共享系统，自行车运营数量超过897万辆［2］。公共自行车对于解决公共交通“最后一公里”难题，倡导绿色出行发挥了重要作用。而现实中自行车站点常常出现无车可借、无桩可还的情况。此时，如何计算自行车系统的服务能力以及在规划DBSS时，如何判断哪些站点将发生空满桩现象，对这些问题的研究对于科学开展DBSS规划与运营调度具有重要的意义。

目前对于DBSS的研究主要聚焦主题有：自行车道网络设计［3］、自行车站选址设计［4］、车队规模设计［5］、自行车搬迁［6-7］、自行车库存水平管理［8-9］以及与公共交通的整合［10］。这些研究试图通过优化算法实现自行车共享系统的最优设计与运营。DBSS有两个显著的特性：（1）用户到达站点的时间间隔是随机的，自行车从租车点到还车点间的骑行时间因用户骑行的异质性也呈随机性，故用户还车间隔也是随机的；（2）投入到自行车共享系统的自行车总数是固定的，且只能在站点停留或在站点间循环。因此，所有的自行车只有两种状态，在站点停留和在道路骑行。从自行车角度来看，这两个特征决定了DBSS本质上属于封闭排队网络。

为了提高DBSS的运营效率，目前的研究主要考虑不确定的有桩自行车共享系统规划。George等［11］基于封闭排队网络研究了自行车可用性与车队规模问题，基于利润最大化给出了最优车队规模。Fricker等［5］提出了同质自行车系统的随机模型，研究了用户到达不确定性对“空满桩”现象的影响及最优车队规模问题。这些研究尽管考虑了需求的不确定性，但忽略了站点停车桩容量限制，从而无法准确分析有桩自行车共享系统服务能力和水平。为此，部分研究引入了停车桩容量限制，考虑借还车失败次数［12-13］、站点空满桩持续时间［14-15］等约束，寻求用户需求最大化目标下的最优站点选址与容量分配方案。但大部分研究未能考虑站点容量限制，无法揭示自行车系统的服务水平与自行车、停车桩分配之间的数学关系，也就无法探索“无车可借，无桩可还”的发生问题。即使有些研究考虑了站点容量限制，但是还没有公开的解决方案和方法来量化DBSS的吞吐率，与现实仍存在一定的差距。

本文对DBSS的服务能力进行了定义，构建了近似的DBSS模型，开发出一种用于计算系统的服务绩效近似算法；同时，探索了自行车系统的运营性质，包括系统吞吐率与自行车投放量的关系，以及站点出现自行车集聚与空缺的判断条件；最后通过一个实际案例验证提出的近似算法和结论，展示其在DBSS中的初步应用。

1 模型构建

1.1 问题描述及假设

考虑一个有桩自行车共享系统，衡量其服务效率最直接指标为单位时间内服务的有效用户人数，即封闭排队网络中的吞吐率［16］，因此本文将在封闭排队网络理论框架下求解有桩自行车共享系统的吞吐率，即用户借车成功离开站点、真正得到站点提供服务的速率。根据上述自行车借还过程，为便于建模特作如下假设：

A1 有桩自行车共享系统由m个站点和n辆自行车组成，每个站点有Bi（i =1，2，…，m）个停车桩，并且任意一对自行车站点之间至少可以双向路径连通；

A2 假设用户到达站点i的时间间隔服从参数λi（i=1，2，…，m）的负指数分布，各站点用户相互独立，用户在站点i以先到先服务规则借还车；

A3 用户从站点i骑自行车到站点j （i， j=1，2，…，m）的选择概率为pij≥0，且∑mj=1pij=1，本文称P=pij为路由矩阵；

A4 用户在站点i、 j间骑行的旅行时间服从参数为τij的独立负指数分布；

A5 对于用户借还车活动，若站点没有可用的自行车时，用户会离开系统；对于用户还车活动，若目的地站点满桩时，用户会骑行至该站点最近站点还车，直至成功为止。

1.2 封闭排队网络分析

对于有桩自行车共享系统构成的封闭排队网络，用户在站点i完成借车后以概率pijj=1，…，m骑行至站点j，该概率满足∑mj=1pij=1 （i=1，…，m），即路由矩阵P是一个马尔可夫转移矩阵，假定该矩阵不可约，以π=π1，π2，…，πm记这个马尔科夫链的平稳概率，即π是

πj=∑mi=1πipij，  ∑mj=1πj=1（1）

的唯一正解。

如果记站点j的自行车平均到达率或平均离开率为aj（n），其中j=1，2，…，m，那么满足

aj（n）=∑mi=1ai（n）pij。（2）

由平稳概率方程可以得到

aj（n）=a（n）πj，其中a（n）=∑mj=1aj（n）。（3）

从该方程可以看到，a（n）是整个系统的自行车平均离开速率，其包括了系统的有效吞吐速率和还车失败速率两部分。

引理1 如果X1，…，Xq是服从均值为λi的独立的泊松随机变量（q=1， 2， …， m），那么Y：=∑qi=1Xi服从均值为∑qi=1λi的泊松分布。

证明 采用数学归纳法证明。设X1～Possionλ1，X2～Possionλ2，X1和X2相互独立，那么对于任意y∈N，

pX1+X2y=∑xpX1kpX2y－k=∑yk=0λk1e－λ1k！·λy－k2e－λ2y－k！

=e－λ1+λ2·λy2·∑yk=0λ1λ2kk！y－k！ =e－λ1+λ2y！λ1+λ2y。（4）

因此，X1+X2～Possionλ1+λ2。现在，假设X1，…，Xq-1是服从均值为λi（ i =1，2，…，q-1）的独立的泊松随机变量，那么X′：=∑q－1i=1Xi服从均值为∑q－1i=1λi的泊松分布。若Xq是独立于X′且服从均值为λq的泊松随机变量，则由公式（4）可得，

pX′+Xqy=e－∑q－1i=1λi+λqy！∑q－1i=1λi+λqy，

p∑qi=1Xiy=e－∑qi=1λiy！∑qi=1λiy。

因此，∑qi=1Xi～Possion∑qi=1λi，证明完毕。

命题1 在有桩自行车共享系统中，如果用户到达站点i服从速率为λi的独立的泊松分布，那么到达站点i的自行车数量也是独立的泊松随机变量。

证明 根据自行车借还过程可知，到站的自行车分为两种类型：第一种是用户自愿归还至目的地站点的自行车；第二种是用户因目的地站点满桩而被迫归还至该站点的自行车。为了证明自行车到达站点的过程服从泊松分布，需通过引理1证明自愿用户和被迫用户的到达过程都服从独立的泊松分布。

如果用户成功将自行车归还到意愿目的地站点，则称这类用户为自愿用户。本文首先证明自愿用户到达站点服从独立的泊松分布。假设用户按速率为λi （i=1，2，…，m） 的泊松过程到达站点i，忽略用户从借到车至离开站点所花费的时间。一个在时刻ss≤t到达站点i的用户，以概率Prent， 1is借车成功，以概率Prent， 2is借不到车（其中∑2j=1Prent，  jis=1）。利用文献［16］中命题5.3可知，直到时刻t为止，在站點i成功借车用户数Nrent， 1it是具有均值ENrent， 1it=λi∫t0Prent， 1isds的独立泊松随机变量。同样，将在站点i （i=1，2，…，m）成功借车的用户分为m 类，每类用户是从站点i自愿还车至每个站点的用户。由于借车成功的用户从每个站点出发是泊松过程，因此从站点i（i=1，2，…，m）至还车站点j（j=1，2，…，m）的自愿用户的到达过程也是独立泊松过程。由引理1可知，任意站点的自愿用户的到达过程也是一个独立的泊松过程。

同理可得，任意站點的被迫用户的到达过程也是一个独立的泊松过程。综上，任意站点的自行车到达数为自愿用户数和被迫用户数的总和。利用引理1可得，任意站点的自行车到达服从泊松分布。

值得注意的是，由命题1可知自行车到达站点过程服从泊松分布，那么自行车到达站点的时间间隔服从负指数分布。因此有桩自行车共享系统在时间长度上是一个无记忆的系统。

基于经典的平均值分析法［17］，可通过两个主要定理（到达定理和Little定律）推导有桩自行车共享系统的吞吐率的近似算法。根据到达定理［16］可知，在有n辆自行车的封闭网络系统中，骑自行车到达站点i的到达者所看到的系统的分布与只有n-1辆自行车的同样的网络系统的平稳分布相同。因此，令ENi（n）为网络中有n辆自行车时停在站点i的平均自行车数量；ETi（n）为网络中有n辆自行车时在站点i的自行车平均停留时间。对一辆到达自行车看到在站点i的自行车数量Ci取期望值，推出

ETi（n）=1+E［Ci］λi=1+ENi（n－1）λi。（5）

系统中的自行车包括在站点停放和正在被使用两类自行车，故n=∑mi=1ENi（n）+∑mi=1∑mj=1ENij（n）。而在站点i的自行车停留的时间为ETi（n），其他站点骑行至站点i的平均旅行时间为∑mj=1pjiτji。因此，系统的自行车平均到达率为

an=n/∑mi=1πiETi（n）+∑mi=1∑mj=1πipijτij。（6）

因此站点的有效吞吐速率为

Hi（n）=min a（n）πi，λi，

其中

Hn=∑mi=1Hi（n）。（7）

利用Little公式可以得到站点i的平均自行车数量为

ENi（n）=min Hi（n）ETi（n），Bi。（8）

根据命题1可知，对于拥有Bi个停车桩站点，自行车的借还过程可以看作是用户与自行车的双排队系统。若站点无自行车，则用户到达站点后即刻离开系统，故站点空桩就不存在顾客排队。因此，任意站点i可以看作是M/M/1/Bi排队系统，状态转移如图1所示。

在该排队系统中，将用户视为服务员，到达的自行车视为作业，则站点i处可停放的自行车上限为Bi个，因此有

λn=ai，      n=0，1，…，Bi-1 0，        n=Bi，  Bi+1，… ，

μn=λi，     n=0，1，…。

根据流入和流出每个状态的期望速率必须相等的条件，可以得到状态k的平衡方程：

aiPxi=k－1+λiPxi=k+1=ai+λiPxi=k，    k=1，2，…，Bi－1。

结合∑Bik=0Pxi=k=1，即可得到站点i无车和满桩的概率分别为

Pxi=0=1－ρi1－ρiBi+1，       ρi≠1 1Bi+1，            ρi=1  ，（9）

Pxi=Bi=1－ρiρiBi1－ρiBi+1，    ρi≠1 1Bi+1，            ρi=1 。（10）

因此，当系统的总自行车投放量超过站点的最小容量时，站点开始存在用户还车失败的情形。根据假设A5可知用户需要去目的地站点的最近站点继续还车，自行车网络的实际转移概率发生变化，即站点j的车辆平均到达率由任意站点的意愿转移速率和被迫转移速率组成。故利用公式（9）～（10）可得由站点i向站点j的实际自行车转移概率为

pij=λi1－Pxi=0pij+aiPxi=Biηij∑mj=1λi1－Pxi=0pij+aiPxi=Biηij=λiρi－ρiBi+1pij+ai1－ρiρiBiηij∑mj=1λiρi－ρiBi+1pij+ai1－ρiρiBiηij， （11）

其中，若站点j 是站点i的最近站点，则ηij=1；否则ηij=0。

1.3 吞吐率的近似算法

利用公式（5）～（11）可以建立计算自行车网络中站点的平均自行车数量、平均等待时间和吞吐率的近似算法，步骤如下：

步骤1 计算初始的马尔科夫链平稳概率，πj=∑mi=1πipij，∑mj=1πj=1;

步骤2 Let ENi（0）=0，i=0，…，m and a（0）=0；

步骤3 For k=1，…，n do

ETi（k）=ENi（k－1）+1/λi;

If k≤min （Bi）then

ak=k/∑mi=1πiETi（k）+∑mi=1∑mj=1πipijτij;

ai（k）=a（k）πi;

Else

pij=λiai（k－1）λi－ai（k－1）λiBi+1pij+ai（k－1）1－ai（k－1）λiai（k－1）λiBiηij∑mj=1λiai（k－1）λi－ai（k－1）λiBi+1pij+ai（k－1）1－ai（k－1）λiai（k－1）λiBiηij;

πj=∑mi=1πipij，    ∑mi=1πj=1;

ak=k/∑mi=1πiETi（k）+∑mi=1∑mj=1πipijτij;

ai（k）=a（k）πi;

End

Hi（k）=min ai（k），λi;

Hk=∑mi=1Hik;

ENik=min Hi（k）ETi（k），Bi;

End

1.4 系统的运营性质

本小节通過考察系统吞吐率与投放自行车数量、停车桩数之间的相互关系，揭示站点产生“无车可借，无桩可还”的发生机制，并给出最优自行车数量的定义，为运营商提升有桩自行车共享系统的服务效率，促进交通绿色可持续发展提供决策依据。

1.4.1 吞吐率

命题2 在一个有桩自行车共享系统中，如果自行车到达站点的时间越早，那么用户骑自行车离开该站点的时间也越早。

证明 令Aik为第k 辆自行车到达站点i的时间，Dik为到达站点i的第k辆自行车的离开时间，Wik为到达站点i的第k辆自行车的停留时间。命题2意味着，对于站点i，若An+1ik≤Anik，k=1，2，…，K，则Dn+1ik≤Dnik，k=1，2，…，K。命题2采用归纳法进行证明。对于K=1， Dn+1i1=An+1i1+Wi1≤Ani1+Wi1=Dni1。假设引理针对K=l成立，即Dn+1il≤Dnil。那么对于K=l + 1， Dn+1i（l+1）=max Dn+1il，An+1i（l+1）+Wi（l+1）≤max Dnil，Ani（l+1）+Wi（l+1）=Dni（l+1），证明完毕。

性质1 在给定停车桩的情况下，有桩自行车共享系统吞吐率随自行车数量的增加呈非递减性，即对于所有的t≥0，有H（n+1）≥H（n）。

证明 采用归纳法，在有n辆公共自行车和m个站点的系统中，令τn1<τn2<…为至少一辆自行车完成服务的瞬时时间，因此将tn定义为在有n辆自行车和n + 1辆自行车系统中至少有一辆自行车完成服务的时间序列，其中t0：=0;ts：=min minτniτni>ts－1，minτn+1iτn+1i>ts－1，s≥1。为了证明DBSS吞吐率随系统自行车数量的增加呈非递减性，即对于t≥0有H（n+1）≥H（n），由于H（n）=limt→∞∑mi=1Dni（t）/t，意味着要证明Dn+1i（t）≥Dni（t），i=1，2，…，m。

当tk= t0 = 0时，Dn+1i（0）=Dni（0）=0，因此Dn+1i（t）≥Dni（t）成立。假设Dn+1i（t）≥Dni（t）对于t0， t1，…，tq成立。令Slj（t）为站点l中第j个离开的自行车在服务完成后将去往的站点。若i=j，则s（i， j）=1；否则为0。Tijk为从站点i到站点j的第k辆自行车的行程时间，Xi（0） 为站点i的初始自行车数量。利用命题2，对于k=1，2，…，q； b = 1， 2，…， m有

An+1i（tk）=∑ml=1∑Dn+1l（tk－Tlij）j=1σ（Slj（tk－Tlij），i）+Xi（0）+1·σ（b，i）

≥∑ml=1∑Dnl（tk－Tlij）j=1σ（Slj（tk－Tlij），i）+Xi（0）=Ani（tk）。

因为An+1i（tk）和Ani（tk）在［tk－1，tk）是恒定的，因此对于t≤tq，An+1i（t）≥Ani（t）。所以得到An+1ij≤Anij，j=1，…，Ani（tq）。根据命题2可知Dn+1ij≤Dnij，j=1，…，Ani（tq）。由于Wij>0，Anij≤tq，对于所有的j有Dnij≤tq+1，那么也遵循Dn+1ij≥Dnij，对于所有的站点j 有Dnij≤tq+1。因此Dn+1i（t）≥Dni（t）对于tq+1也成立，证明完毕。

性质1表明有桩自行车共享系统的有效吞吐率随着自行车数量的递增呈非递减性。然而，本文将在第2.2节中看到，有桩自行车共享系统的有效吞吐率随着自行车数量的增加而增加，但存在一个上限。因此，可能存在一个自行车临界值阻止吞吐率的增加。通过以下的定义，可以得出在DBSS中最优的自行车数量以及如何寻找该最优值。

定义1 最优自行车数量：对于一个有桩自行车共享系统，若满足以下条件，则可以确定系统的最优自行车数量

nOPT=max kHk－Hk－1>0  且  Hk+1－Hk=0且k∈argmax H（l），l∈Z+，k∈Z+。

值得注意的是，在本文设计的近似算法中，迭代计算了H（k）和H（k-1），因此系统的最优自行车数量很容易确定。

1.4.2 空满桩的判断

在有桩自行车共享系统中，站点所有的车桩如果长时间出现空桩，用户将无法借车；如果长时间出现满桩，用户将无法还车。如果自行车共享系统多个站点长时间空满桩将显著恶化用户体验，可能迫使公共自行车用户转移到其他交通方式。因此，有必要诊断有桩自行车共享系统站点是否会发生空满桩。

定义2 对于一个带有Bi个停车桩的站点i，若满足

（1） 站点i的平均自行车数量低于φ1Bi的概率大于ω1，即Pxi<φ1Bi」>ω1，则称该站点为自行车空缺的；

（2） 站点i的平均自行车数量高于φ2Bi的概率大于ω2，即Pxi>φ2Bi」>ω2，则称该站点为自行车集聚的。

其中φ1和φ2为比例参数，且0<φ1，φ2，ω1，ω2<1；符号“·」”表示向下取整数。

命题3 自行车集聚与空缺的判断条件：对于任意站点i，当自行车到达率ai和用户到达率λi满足下列条件（1）～ （3）中的任意一条，可判断该站点的自行车库存情况：

（1） 若满足下面的条件，则站点i会产生自行车集聚情况

aφ2Bi」+1i·λBi－φ2Bi」i－aBi+1iλBi+1i－aBi+1i>ω2，当aiλi≠1时Bi－φ2Bi」Bi+1>ω2，                     當aiλi=1时；（12）

（2） 若满足下面的条件，则站点i会产生自行车空缺情况

λBi+1i－aφ1Bi」i·λBi－φ1Bi」+1iλBi+1i－aBi+1i>ω1，当aiλi≠1时φ1Bi」Bi+1>ω1，                            当aiλi=1时；（13）

（3） 若满足下面的条件，则站点i自行车既不集聚也不空缺

λBi+1i－aφ1Bi」i·λBi－φ1Bi」+1iλBi+1i－aBi+1i≤ω1且aφ2Bi」+1i·λBi－φ2Bi」i－aBi+1iλBi+1i－aBi+1i≤ω2， 当aiλi≠1时φ1Bi」Bi+1≤ω1且Bi－φ2Bi」Bi+1≤ω2，                                                当aiλi=1时。（14）

证明 在平稳状态下，若站点i自行车产生集聚，需要满足

Pxi>φ2Bi」>ω2。（15）

当ρi≠1（其中ρi=ai/λi）时，则不等式（15）可化简为Pxi>φ2Bi」=ρφ2Bi」+1i－ρBi+1i/1－ρBi+1i>ω2，即满足条件ρφ2Bi」+1i－ρBi+1i/1－ρBi+1i>ω，

则站点i自行车会产生集聚。当ρi=1时，则不等式（15）可化简为Pxi>φ2Bi」=Bi－φ2Bi」/Bi+1>ω2，即满足条件Bi－φ2Bi」/Bi+1>ω2，则站点i自行车会产生集聚。站点自行车产生空缺或既不集聚也不空缺的证明与上述过程类似，不再赘述。

推论1 若定义自行车空缺站点为平均自行车数量为0的概率大于ω，即Pxi=0>ω；自行车集聚站点为平均自行车数量为Bi的概率大于ω，即Pxi=Bi>ω。那么对于任意站点i，当自行车到达率ai和用户到达率λi满足下列条件（1）～ （3）中的任意一条，可判断该站点的自行车库存情况：

（1） 若满足下面的条件，则站点i会产生自行车集聚情况

aBii∑Bik=0λBi－kiaki>ω，当aiλi≠1时1Bi+1>ω，             当aiλi=1时；（16）

（2） 若满足下面的条件，则站点i会产生自行车空缺情况

λBii∑Bik=0λBi－kiaki>ω，当aiλi≠1时1Bi+1>ω，             当aiλi=1时；（17）

（3） 若满足下面的条件，则站点i自行车既不集聚也不空缺

λBii∑Bik=0λBi－kiaki≤ω且aBii∑Bik=0λBi－kiaki≤ω，当aiλi≠1时1Bi+1≤ω，                                              当aiλi=1时。（18）

证明过程与命题3类似，在此不再赘述。

值得注意的是，为了避免空满桩现象，有桩自行车共享系统均须开展自行车的再分布调度，以平衡各个站点的自行车数量。命题3及其推论1能够揭示有桩自行车共享系统中哪些站点发生自行车空缺和集聚。这将为自行车共享系统的站点选址、自行车规划提供决策支持，也能为公共自行车再分布调度中的取送起讫点及路径规划、空满桩站点自行车取送数量等提供关键支撑。

2 案例应用

2.1 案例介绍

本研究以苏州独墅湖科教创新区的自行车共享系统作为例，验证本文模型。该系统共有37个自行车站点，停车桩总数为1 260个，平均自行车总数为442个，站点和停车桩的具体分布如图2所示。系统运营商提供了该区域内2019年10月12日24 h的2 078次自行车出行数据，这些数据记录了高峰时期用户借还自行车的时间及站点、车桩及用户ID号。利用该数据统计得到自行车共享系统平均有效吞吐率为86.58人次/h。由于站点空桩情况下会出现用户流失，故利用该数据统计各站点的空桩时段，将非空桩期间的用户到达各站点次数按照时间比例填补到空桩时段，将其作为各个站点实际用户到达率。利用原始数据还统计了行程时间矩阵、路由矩阵和各站点的最近站点（最近站点见表1所示）。由于篇幅原因，本文不再列出行程时间矩阵和路由矩阵。

2.2 結果分析

2.2.1 系统吞吐率

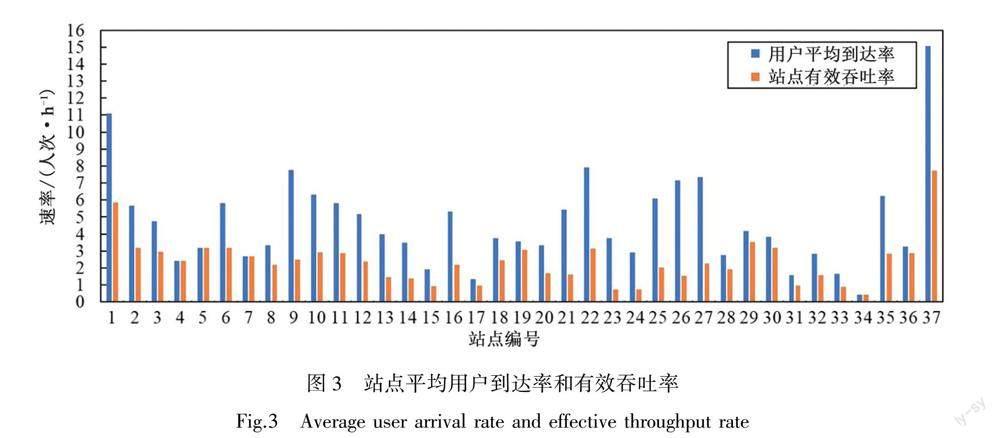
根据近似模型计算得到的系统有效吞吐率为88.36人次/h，与真实吞吐率相对误差为2.04%。图3给出了站点的平均用户到达率和有效吞吐率。可以看到，只有4个站点（4号、5号、7号、34号）的用户需求完全得到了满足，即站点的有效吞吐率与用户平均到达率相等。其余站点的供给与用户需求不匹配，其中，1号、9号、22号、26号、27号、37号站点供不应求的情况极为显著，平均每小时有5名以上用户不能借到自行车。这说明目前研究区域内有桩自行车共享系统的自行车分布极不平衡，系统内自行车自循环结果在很大程度上无法满足用户的需求。

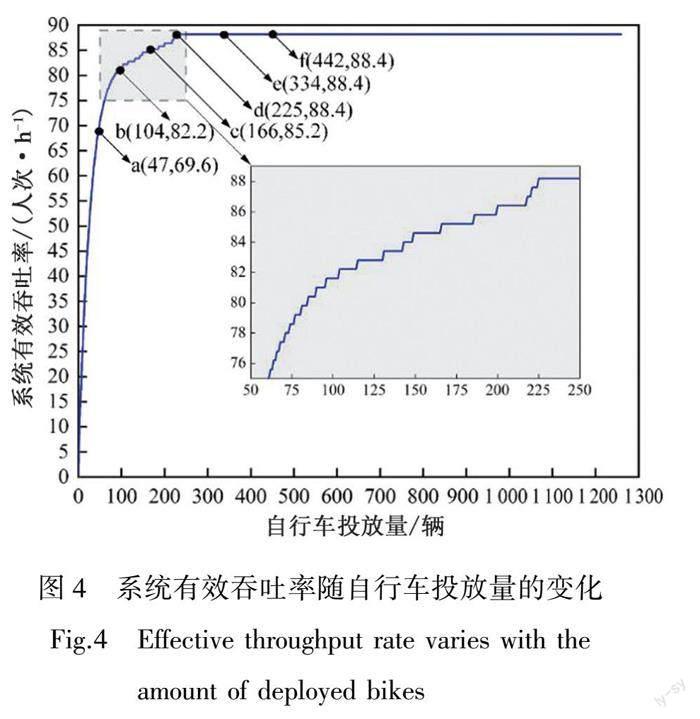
图4给出了系统有效吞吐速率与自行车投放量之间的关系。由图可知，随着自行车投放量的增加，系统有效吞吐率呈现阶梯式的递增趋势，当自行车投放量大于225辆后，系统有效吞吐率保持不变，验证了性质1。根据定义1可知，该有桩自行车共享系统的最优自行车投放量为225辆，此时系统有效吞吐率达到最大值88.4人次/h。但是该系统实际的自行车投放量为442辆，故系统自行车数量明显过剩。

2.2.2 空满桩t分析

一般来说，如果自行车共享系统具有较好的服务水平，当站点处于还车高峰时，站点仍需保留20%的空桩；反之，当站点处于借车高峰时，站点也需要配备20%的车桩应有的自行车数［18］。因此，结合空满桩的定义，本文将定义2的比例参数设置为φ1=0.2，φ2=0.8，概率参数ω1=ω2=0.8。

图5给出了站点自行车库存的平均值以及平衡自行车数的区间。可以看出，绝大多数站点自行车库存极为紧缺，少量站点库存爆满，还有极少数的站点的平均库存处于平衡区间内。图6为自行车投放量442辆下各站点自行车平均停留时间。可以看出，自行车在站点4、5、7、34的平均停留时间超过10 h，在其他站点的停留时间在0.1～2.0 h范围内。上述进一步验证了自行车在站点4、5、7、34的严重集聚状态以及其他站点自行车库存普遍紧缺情况。

自行车投放量的增加会改变自行车集聚与空缺站点的空间分布。利用命题3计算得到图4中a、b、c、d、e、f等6个点对应的自行车投放量下，站点的集聚和空缺概率，具体的空间分布如图7所示。可以看出，随着自行车投放量的增加，站点4、5、7、34从空缺站点逐渐转化为集聚站点，站点29、36、39从空缺站点转化为自行车既不集聚也不空缺站点，其他站点始终处于自行车空缺状态。随着自行车投放量的增长超过225辆，自行车集聚与空缺站点分布基本不再变化，投入的大量的自行车将迫使大量用户在最近站点间骑行，试图寻找最近站点还车。

3 总结

本文基于封闭排队网络构造了有桩自行车共享系统吞吐率近似算法，考察了系统的运营性质。理论上证明了有桩自行车共享系统吞吐率随自行车投放量的增加呈非递减性，给出了站点产生自行车集聚与空缺的判断依据。以苏州市为例进行了上述算法的应用与结论的验证，给出了该有桩自行车共享系统的服务绩效。研究表明，随着自行车投放量增长，吞吐率呈阶梯式递增且达到最大值后保持不变；自行车投放量一旦超过最优数量将产生闲置，并且自行车集聚与空缺站点分布也将固定。

依托本文建立的近似模型，可进一步从多个方面进行拓展，例如：本研究考虑的用户到达自行车站点借车为平稳随机过程，未来可以考虑用户到达存在早晚高峰的非平稳过程；本研究中自行车最优投放量并未考虑车站选址、车站间距、用户骑行距离等因素，未来应考虑这些因素对有桩自行车共享系统的最优规划设计问题。

参考文献：

［1］ZHANG J， MENG M， WONG Y D， et al. A data-driven dynamic repositioning model in bicycle-sharing systems［J］. International Journal of Production Economics， 2021， 231： 107909. DOI： 10.1016/j.ijpe.2020.107909.

［2］MEDDINR， DEMIAO P. The bike-sharing world map ［EB/OL］. ［2022-12-31］.https：//www.metrobike.net/.

［3］LIN J J， YU C J. A bikeway network design model for urban areas［J］. Transportation， 2013， 40（1）： 45-68. DOI： 10.1007/s11116-012-9409-6.

［4］MIX R， HURTUBIA R， RAVEAU S. Optimal location of bike-sharing stations： a built environment and accessibility approach［J］. Transportation Research Part A： Policy and Practice， 2022， 160： 126-142. DOI： 10.1016/j.tra.2022.03.022.

［5］FRICKER C， GAST N. Incentives and redistribution in homogeneous bike-sharing systems with stations of finite capacity［J］. EURO Journal on Transportation and Logistics， 2016， 5（3）： 261-291. DOI： 10.1007/s13676-014-0053-5.

［6］NEUMANN-SAAVEDRA B A， MATTFELD D C， HEWITT M. Assessing the operational impact of tactical planning models for bike-sharing redistribution［J］. Transportation Research Part A： Policy and Practice， 2021， 150： 216-235. DOI： 10.1016/j.tra.2021.06.003.

［7］LV C， ZHANG C Y， LIAN K L， et al. A two-echelon fuzzyclustering based heuristic for large-scale bike sharing repositioning problem［J］. Transportation Research Part B： Methodological， 2022， 160： 54-75. DOI： 10.1016/j.trb.2022.04.003.

［8］FU C Y， MA S F， ZHU N， et al. Bike-sharing inventory management for market expansion［J］. Transportation Research Part B： Methodological， 2022， 162： 28-54. DOI： 10.1016/j.trb.2022.05.009.

［9］GAMMELLI D， WANG Y H， PRAK D， et al. Predictive and prescriptive performance of bike-sharing demand forecasts for inventory management［J］. Transportation Research Part C： Emerging Technologies， 2022， 138： 103571. DOI： 10.1016/j.trc.2022.103571.

［10］LUO X L， GU W H， FAN W B. Joint design of shared-bike and transit services in corridors［J］. Transportation Research Part C： Emerging Technologies， 2021， 132： 103366. DOI： 10.1016/j.trc.2021.103366.

［11］GEORGE D K， XIA C H. Fleet-sizing and service availability for a vehicle rental system via closed queueing networks［J］. European Journal of Operational Research， 2011， 211（1）： 198-207. DOI： 10.1016/j.ejor.2010.12.015.

［12］ELEBI D， YRSN A， IK H. Bicycle sharing system design with capacity allocations［J］. Transportation Research Part B： Methodological， 2018， 114： 86-98. DOI： 10.1016/j.trb.2018.05.018.

［13］MALEKI VISHKAEI B， MAHDAVI I， MAHDAVI-AMIRI N， et al. Balancing public bicycle sharing system using inventory critical levels in queuing network［J］. Computers & Industrial Engineering， 2020， 141： 106277. DOI： 10.1016/j.cie.2020.106277.

［14］KASPI M， RAVIV T， TZUR M. Bike-sharing systems： User dissatisfaction in the presence of unusable bicycles［J］. IISE Transactions， 2017， 49（2）： 144-158. DOI： 10.1080/0740817x.2016.1224960.

［15］CAGGIANI L， CAMPOREALE R， MARINELLI M， et al. User satisfaction based model for resource allocation in bike-sharing systems［J］. Transport Policy， 2019， 80： 117-126. DOI： 10.1016/j.tranpol.2018.03.003.

［16］ROSS S M. Introduction to probability models［M］. 10th ed. Amsterdam： Elsevier Academic Press， 2010.

［17］REISER M， LAVENBERG SS. Mean-value analysis of closed multichain queuing networks［J］. Journal of the ACM， 1980， 27（2）： 313-322. DOI： 10.1145/322186.322195.

［18］蔣琳. 城市公共自行车系统调度模型及算法研究［D］.兰州：兰州交通大学， 2017.