选矿机械精密零件钻孔误差补偿方法研究

彭 锋

(1.都兰金辉矿业有限公司,青海 都兰 816100) (2.青海省第六地质勘查院,青海 格尔木 816000)

选矿机械作为重型机械设备,由数量较多的精密零件组成,这些零件通常需要采用数控机床进行加工。在高效生产条件下,对选矿机械精密零件的加工过程会存在不同程度的误差,导致零件出现缺陷[1-3]。因此,为了提升选矿机械精密零件钻孔精度,就需要对误差进行补偿[4]。

近年来,国内外诸多学者针对零件加工误差补偿问题进行了大量研究,如米良等[5]利用机床运动直线度检测方法分离零件测量误差和轴运动直线度误差,并在刀架系统动力学模型的基础上,依据压电陶瓷与柔性铰链导向,设计出一套微动刀架,利用分离出的轴运动直线度误差与微动刀架完成精密零件误差的补偿;向华等[6]首先利用比对仪实时获取精密零件表面点的坐标,然后通过局部多项式回归方法,对精密零件系统误差进行建模,并构建模型点的指令域映射关系,最后利用该关系分解系统误差分量,借助双码联控技术完成零件加工误差补偿。上述两种方法虽然在一定程度上对零件加工误差进行了补偿,但是第一种方法没有考虑补偿方法的实时性,不能满足实际生产需求;第二种方法则忽略了零件加工过程中随机误差对零件加工精度的影响,达不到理想的补偿效果。

选矿机械作为机械工业领域内的重要分支,主要为原材料工业服务,其性能与质量既关系到选矿的生产质量与效益,也关系到生产的安全性[7-9]。因此,本文提出选矿机械精密零件钻孔误差补偿方法,利用该方法对精密零件钻孔误差进行补偿,以保证选矿机械精密零件加工的精度。

1 选矿机械精密零件钻孔误差补偿方法设计

对于零件误差补偿问题,主要通过两种方法来实现:硬补偿、软补偿[10-11]。其中软补偿具有较好的灵活性与经济性,因此本文采取软补偿方法对选矿机械精密零件钻孔误差进行补偿。

1.1 选矿机械精密零件钻孔误差实时检测与补偿原理

选矿机械精密零件钻孔误差实时检测模块结构如图1所示。测量程序利用RS-232串行接口将其传输至加工中心(CNC)。CNC负责将接收到的测量指令发布至测头,测头根据测量程序安排好的线路朝着测量点移动。在测头触碰到零件时,便会放射出相关的数据信号,利用相关接口将信号传输至转换器,经过转换处理后传输回CNC。坐标信息利用RS-232串行通讯接口将保存的信息传输给计算机。将获取的测量结果与理想坐标进行对比,便能够获得选矿机械精密零件钻孔的误差,在加工机床的数控系统中,依据误差对加工编程坐标的代码实施修改,便能完成对选矿机械精密零件钻孔的误差补偿。

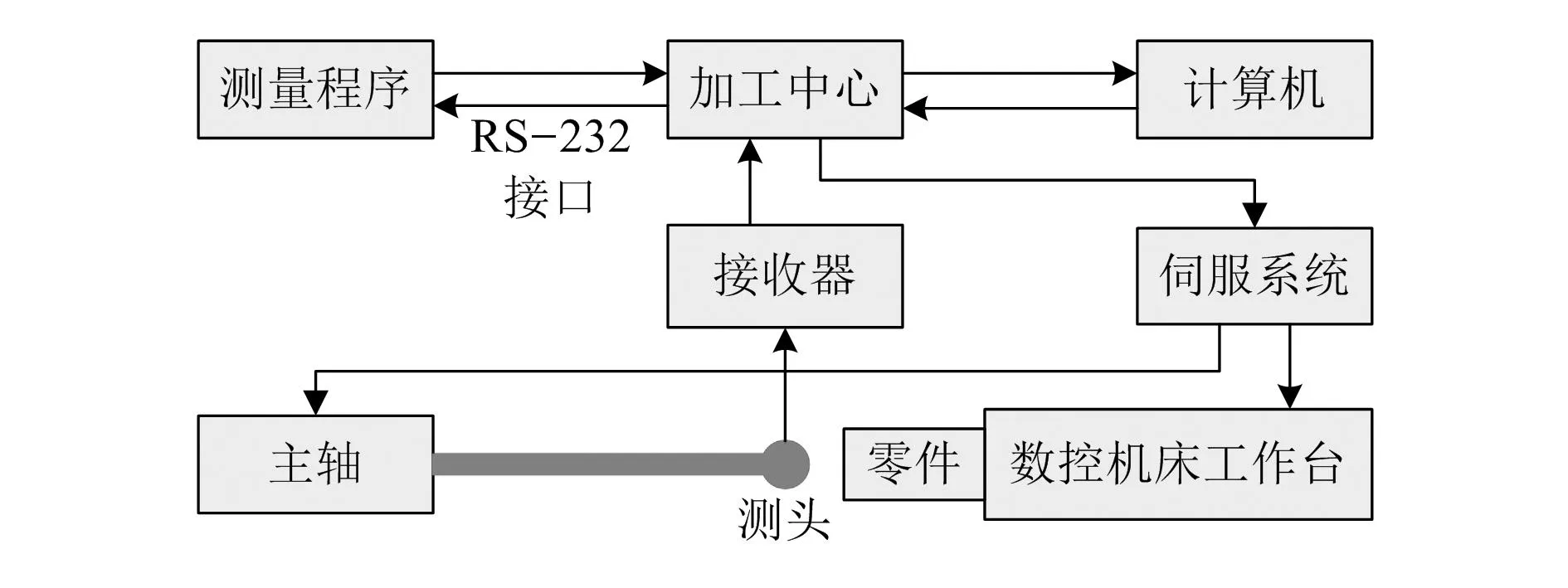
图1 选矿机械精密零件钻孔误差实时检测模块结构图

1.2 选矿机械精密零件钻孔加工动态误差分析

构建选矿机械精密零件钻孔加工机床的基坐标系时,钻孔刀具点的矢量化应符合下面的要求:

(1)

式中:λb、sb、ζb分别为刀具点的矢量化,下标b表示钻孔刀具。

从式(1)可知,已知2个刀具点的矢量化,便可以求得第3个矢变量。设置加工机床轴关节数据后,便可以获取工具坐标系的位姿,即选矿机械精密零件钻孔加工机床运动学模型:

(2)

式中:G为工具坐标系位姿,下标x、y、z表示机床基坐标系,O为坐标原点,τ为运动距离,a为钻孔机床,b为钻孔刀具。

为了对钻孔误差源进行精准分析,可以利用机器人D-H模型求得选矿机械精密零件钻孔加工机床关节轴移动量和G中各元素的映射关系,将机床本体作为多个连杆串联结构,建立一个关节坐标系,可以获取其空间变换关系,描述为:

(3)

根据选矿机械精密零件钻孔加工机床的运动学模型和空间变换关系,考虑精密零件加工特点和所有工序的钻孔状态矢量,将当前工序精密零件钻孔加工动态误差描述为以下形式:

Qk=AkQk-1+Ek+Hk+Wk

(4)

式中:Qk为当前工序精密零件钻孔加工动态误差;下标k为工序序号;A为零件误差传递矩阵;E为制造误差,通常由夹具误差导致;H为直接加工误差;W为噪声造成的其他误差。

从误差类型来看,可将式(4)中的误差分为两种,即F1=AkQk-1+Ek+Hk,是系统误差,而F2=Wk,是随机误差。

1.3 基于曲面回归模型的钻孔曲面实时检测

选矿机械精密零件钻孔曲面轮廓朝向坐标轴线方向的两个矢量参数用u和v描述,该零件钻孔部位的实际加工曲面与理想加工曲面分别用A(u,v)和B(u,v)描述,则有:

A(u,v)=B(u,v)+F1(u,v)+F2(u,v)

(5)

设C(u,v)=B(u,v)+F1(u,v),是选矿机械精密零件钻孔部位理想曲面和系统误差叠加产生的新曲面。因为B(u,v)具有确定性,而F1(u,v)则是相对稳定,所以把C(u,v)定义为回归模型,利用C(u,v)表示加工状态下的选矿机械精密零件钻孔检测曲面。因为F2(u,v)具有随机性与不确定性,所以将其设定为服从空间独立分布的变量,用于表示选矿机械精密零件钻孔误差中的随机误差。

为了实现选矿机械精密零件钻孔过程的分段连续加工,并得到检测曲面模型,本文采用双三次B样条曲面对其进行构建,描述为:

(6)

式中:Ui(u)、Vj(v)为基函数,Rij为控制点,h为选矿机械精密零件钻孔深度,l为选矿机械精密零件钻孔直径,h×l为选矿机械精密零件钻孔的曲面片数量。

由于三次B样条曲面模型实际上就是其基函数张量积和R的线性组合,因此可以将式(6)变换为:

(7)

其中:

RK=[xr,K,yr,K,zr,K]T

M=(h+3)(l+3)

式中:XK和RK分别为第K个基函数张量积及其对应控制点,M为控制点总数,xr,K、yr,K、zr,K分别为第K个控制点的机床基坐标系坐标。本文用XK和RK的线性组合构建三次B样条曲面模型。

如果在已加工的选矿机械精密零件钻孔曲面得到了N个检测点的坐标信息,描述为Pw(w=0,1,…,N),并且参数u和v的值以及二者方向上的节点矢量和检测曲面片数量均是已知量,则式(7)中的XK便可以被求取。

综上分析,关于选矿机械精密零件钻孔检测曲面控制点的线性回归模型,通过矩阵P便可以进行描述,即:

P=XR

(8)

式中:P为线性回归矩阵,X为与选矿机械精密零件钻孔检测曲面模型和各个检测点有关的张量积,R为选矿机械精密零件钻孔检测曲面的控制点。

关于R的线性回归模型的最小二乘估计值R′可以描述为:

R′=(XXT)-1XTP

(9)

通常情况下,由于选矿机械精密零件钻孔误差会大大小于钻孔的尺寸规格,因此回归模型测点的两个参数u和v的大小可以等同于理想曲面中u和v的大小。选矿机械精密零件钻孔检测曲面的预测回归模型S′(u,v)可以描述为:

(10)

通过对回归模型的拟合操作,可以得到关于选矿机械精密零件钻孔的偏差e,描述为:

e=P-XR′

(11)

1.4 选矿机械精密零件钻孔误差的实时补偿

(12)

其中:

(13)

式中:ωij为点j对点i的度量权重。

根据莫兰指数可以获取到检验统计量T:

T=(I-μ)/σ

(14)

式中:μ和σ分别为莫兰指数平均值与方差。

在获取到e后,可以利用T来确定选矿机械精密零件钻孔的随机误差,进而完成误差的分解。

设T′为T的临界值,且T′表现为标准正态分布。当TT′时,则说明偏差中不仅包含随机误差还包含系统误差,此时便需要重新对选矿机械精密零件钻孔检测曲面的回归模型进行构建,经过多次迭代,直至偏差呈空间独立性分布,方可完成对误差的分解,进而求得系统误差与随机误差。

(15)

根据式(15)可以求得补偿点的补偿量,根据补偿量对选矿机械精密零件钻孔加工机床数控系统内的代码进行修改,建立新的刀具移动线路,从而完成对选矿机械精密零件钻孔误差的补偿。

2 实验结果与分析

以某液压缸筒体为实验对象,参考某机械厂的钻孔工序,搭建实验环境,作为基础实验环境。实验步骤:首先采用在线监测的方式对某液压缸筒体钻孔误差进行实时监测;其次用获取的工具坐标系位姿构建加工机床的运动学模型,利用D-H模型求得某液压缸筒体钻孔加工机床关节轴移动量和G中各元素的映射关系;再次采用双三次B样条曲面,构建某液压缸筒体钻孔检测曲面的预测回归模型;随后采用莫兰指数法对某液压缸筒体钻孔误差实施分解,求得系统误差与随机误差,并根据式(15)计算补偿量;最后根据补偿量对某液压缸筒体钻孔加工机床数控系统内的代码进行修改,建立新的刀具移动线路,重新进行加工,结果证明已完成对某液压缸筒体钻孔误差的补偿。

利用某型号的加工机床对该液压缸筒体进行钻孔加工,该机床为立式数控钻床,可加工的材质为金属和聚合物,支持定制,主要技术参数见表1。

利用本文方法对液压缸筒体钻孔相关数据进行实时检测,得到的结果见表2。由表可知,利用本文方法可以实时测得液压缸筒体钻孔各个测点坐标的实时数据,从而可以获取液压缸筒体钻孔误差。

表2 液压缸筒体钻孔坐标实时检测数据 单位:mm

利用本文所提莫兰指数方法对液压缸筒体钻孔误差实施分解操作,得到的结果如图2所示。依据图2误差分解结果,采用本文方法对液压缸筒体钻孔误差进行补偿后的各测点坐标数据与理想状态下坐标数据的对比情况,见表3。

表3 液压缸筒体钻孔误差补偿后坐标数据与理想坐标数据对比 单位:mm

图2 误差分解结果

分析表3可知,所有测点经过误差补偿后的坐标数据与理想状态下坐标数据只存在较小的差异,平均差异仅为0.009 2 mm,即使最大差异也未超过0.013 0 mm。综上可以看出,本文方法可以有效地对选矿机械精密零件钻孔误差进行补偿,效果较好,具有较高的应用价值。

为了进一步验证本文方法补偿选矿机械精密零件钻孔误差的性能。在不同钻孔直径条件下,分别加工了深度为30 mm、60 mm和90 mm的钻孔,并利用本文方法对钻孔误差进行了补偿,经过测试,得出了不同情况下的加工精度,结果如图3所示。

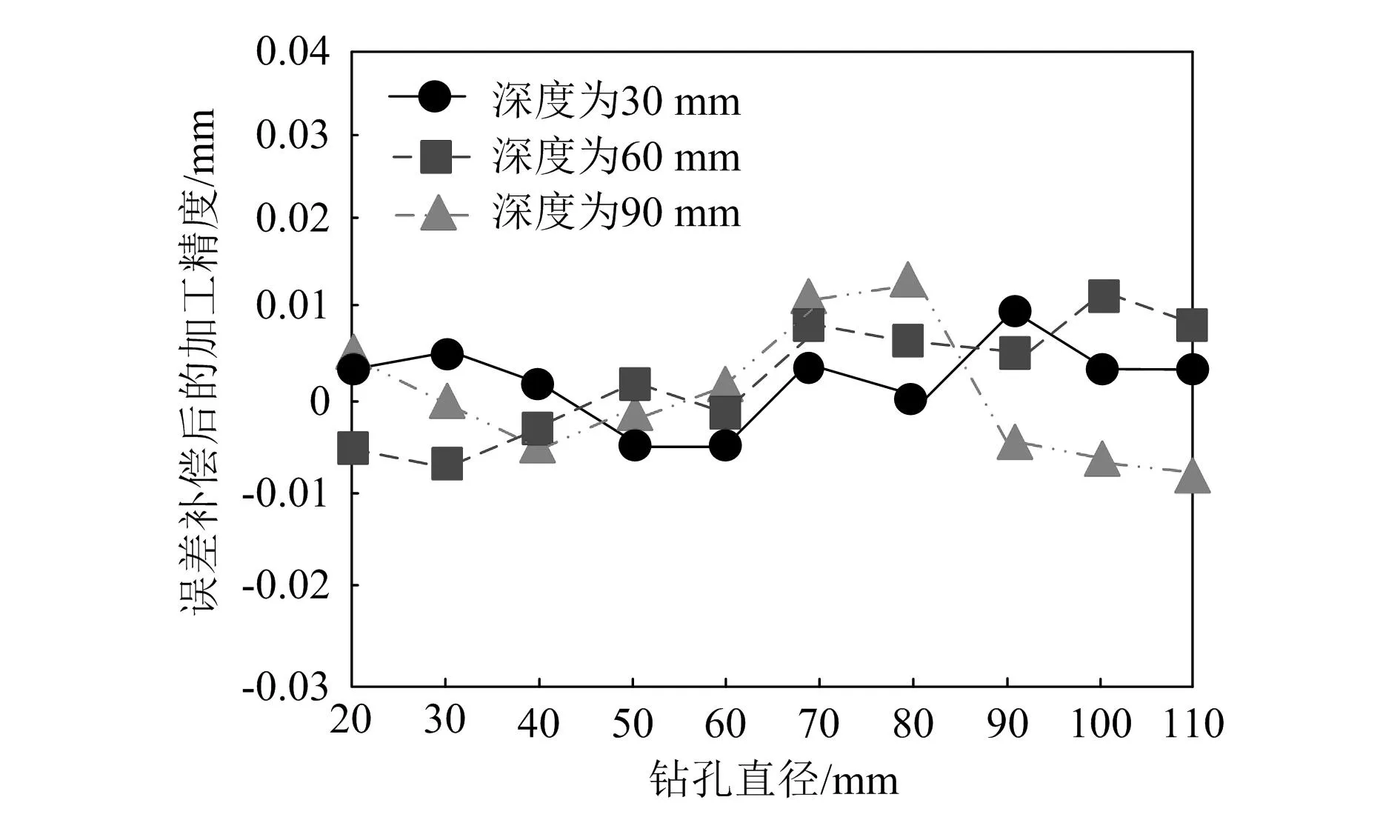
图3 不同钻孔直径条件下钻孔误差补偿后的加工精度

由图3可知,使用本文方法在不同钻孔直径条件下,对钻孔误差进行补偿后,得到的不同规格的钻孔加工精度均在±0.015 mm的范围内浮动,远远优于标准精度范围,特别是钻孔直径为80 mm、深度为30 mm的钻孔加工误差几乎为0 mm。由此可以看出,本文方法具有较高的准确性与稳定性。

3 结束语

选矿机械是选矿生产过程中不可或缺的装备,因此对选矿机械精密零件加工质量的要求越来越严格。因为机床、钻孔仪器等设备均会引起钻孔误差,影响选矿机械精密零件的最终精度,所以本文提出了选矿机械精密零件钻孔误差补偿方法。该方法摒弃了传统的硬补偿方法,通过软补偿方法,借助曲面回归模型对选矿机械精密零件钻孔误差进行了在线检测,进而完成误差的实时补偿。实验证明,本文方法在选矿机械精密零件误差补偿方面有着较好的表现,比较适合解决此类问题。