基于IPSO-BP神经网络的WSNs数据融合算法*

马占飞，巩传胜，李克见，林继祥，刘雨忻

（1.内蒙古科技大学包头师范学院，内蒙古 包头 014010；2.内蒙古科技大学信息工程学院，内蒙古 包头 014010）

0 引 言

针对无线传感器网络（wireless sensor networks，WSNs）因传输大量冗余数据导致高能耗的问题［1］，大量学者将基于神经网络的数据融合技术引进到WSNs 中，对监测数据进行融合处理，以提高数据的采集精度和节约网络能量。文献［2］设计了一种基于反向传播（back propagation，BP）神经网络的WSNs［3］数据融合算法，实验表明，该算法能显著减少数据冗余，降低数据通信量。文献［4 ～6］分别使用遗传算法（genetic algorithm，GA）、萤火虫算法（firefly algorithm，FA）和蚁群优化（ant colony optimization，ACO）算法对BP神经网络的初始网络参数进行优化，以提高BP 神经网络的稳定性和收敛速度，实验表明，优化后的BP神经网络能有效去除冗余数据且提高数据融合精度。文献［7］提出使用粒子群优化（particle swarm optimization，PSO）算法优化BP神经网络的数据融合算法--PSO-BP算法，通过PSO算法优化BP神经网络的初值，并与分簇路由协议结合，能有效提升数据采集效率，延长网络生命周期。但PSO 算法存在易陷入局部最优、早熟收敛等问题。文献［8］提出用天牛须搜索（beetle antennae search，BAS）算法改进PSO 优化BP的WSNs数据融合算法--BSO-BP算法，实验结果表明：该算法能有效提高数据融合精度和网络收敛速度。但该算法没有综合考虑局部寻优与全局搜索之间的平衡问题，也没有解决粒子群易陷入局部最优的缺陷。

针对上述问题，本文从优化粒子群寻优性能和提高BP神经网络数据融合精度的角度出发，在传统PSO算法中引入细菌觅食优化（bacterial foraging optimization，BFO）算法的趋化、迁徙算子进行改进，提出一种基于改进PSO（improved PSO，IPSO）-BP神经网络的WSNs数据融合算法。

1 IPSO算法

1.1 经典PSO算法

PSO算法的寻优公式如下

式中d＝1，2，…，D，D为粒子总维度；i＝1，2，…，N，N为粒子种群大小；k为当前迭代次数；为第k次迭代粒子i的第d维位置；为第k次迭代粒子i的第d维速度；w为惯性权重；c1和c2为学习因子；r1，r2为［0，1］之间的随机数为第k次迭代粒子i的历史最优位置；为第k次迭代粒子群体的历史最优位置。

1.2 基于BFO算法对PSO算法的改进

1.2.1 趋化算子对PSO算法的改进

细菌趋化操作是模拟大肠杆菌的游动和翻转的过程。其实质是细菌在一定空间下搜索自己位置的邻域，由适应度函数值的好坏决定其搜索方向。细菌的位置更新公式如下

式中P（i，j，k，l）为细菌i在第j次趋化、第k次繁殖和第l次迁移操作后的位置，C（i）为细菌翻转中指定方向上的单位步长，φ（i）为细菌翻转后的单位随机方向向量。当细菌搜索目标区域时，其游动的步长和翻转的方向会直接影响算法效果，因此，本文在基础细菌趋化操作中改用自适应游动步长代替固定步长，加快算法收敛。同时加入对翻转方向的限制，根据细菌自身位置和全局最优点之间的距离来调节步长，若两者距离远，则增加步长，反之减少步长。改进后的趋化操作通过细菌在不同的维度前进不同的步长，达到前期搜索效率高，后期搜索精度高的目的。改进后的自适应步长公式如下

式中Cmax＝（Maxd-Mind）／4，Maxd为第d维寻优范围最大值，Mind为第d维寻优范围最小值，Cmax值根据文献［9］采用最大寻优范围值的1／4，j为当前趋化次数，Ji为当前细菌的适应度值，Jmax为当前所有细菌的最大适应度值，rand为［0，1］上的随机数。

在PSO算法中赋予粒子以细菌的趋化行为后，将改善粒子在搜索过程中由于速度过快而错失局部最优解的问题，增强PSO算法局部寻优能力。本文根据适应度轮盘赌方法［8］选取T个粒子进行趋化操作，粒子选取公式为

式中T为当前迭代次数中被选中的粒子总数，iter和maxgen为当前迭代次数和最大迭代次数，i为被选中粒子的编号，N为种群大小。由于PSO算法初期在“跟随”思想指引下，造成局部搜索能力差的缺点，故本文在PSO 算法每次迭代更新后选取T个粒子在自身当前位置进行趋化操作，以增强粒子在初期的局部搜索能力，而随着迭代次数的增加，种群的适应度越来越好，选取的粒子数量也会逐步减少，这有利于算法快速收敛和减少计算量。式（6）为选中的粒子在趋化操作完成后的行为增量

式中Gbest_BFO为粒子群经过趋化操作后的全局最优位置，λ为趋化行为增量因子，w为惯性权重。出于平衡粒子群局部寻优和全局搜索的思想，本文采用凸函数递减法［10］来自适应调整惯性权重w的值，其在收敛速度方面明显优于传统的常数型惯性权重，其公式如下

式中wmax，wmin为最大和最小惯性权重，c1和c2为粒子对自身历史最优经验的学习和粒子对群体最优经验的学习［11］。PSO算法在搜索初期，全局搜索性能较强，而局部搜索性能较差，故参数c1和c2要随着迭代次数递减和递增

式中cm和cn为常数，满足cm＞cn。

IPSO算法中λ为趋化行为增量因子，算法前期较大的趋化行为增量可提高全局搜索能力，而后期随着具有趋化行为的粒子数量减少，较小的趋化行为增量可提高搜索精度，加快算法收敛速度，因此λ的赋值公式如下

式中 λmax和λmin分别为增量权重因子的上、下限值。

1.2.2 迁移算子对PSO算法的改进

在PSO算法陷入局部最优时赋予粒子以细菌的迁移行为能使算法快速跳出局部最优。本文根据文献［12］采用种群适应度方差σ2来判断算法早熟现象，先设定一个适应度方差阈值，当出现时，则认为算法陷入局部最优。

σ2计算方法如下所示

式中为当前种群的平均适应度值，fi为粒子i的适应度值，N为种群规模，种群σ2值越小说明种群的个体聚集程度越高，种群多样性越差。F为归一化因子，取值如下

在此采用自适应的迁移概率对适应度差的粒子进行迁移操作，其公式如下

式中Jmin为细菌当前最小适应度值，Ped为设置的固定迁徙概率。

改进的迁移概率使得适应度低的细菌迁移概率大，适应度高的细菌迁移概率小。这样使得觅食能力好的细菌一定会被迁移，从而能有效保存种群当前精英个体，加速种群进化，跳出局部最优解。

2 IPSO-BP神经网络数据融合算法

2.1 算法网络模型

利用IPSO 优化BP 神经网络数据融合算法并与LEACH分簇路由协议相结合，构建WSNs 数据融合模型。首先，分簇路由协议将WSNs分为大小不同的簇，簇成员节点对采集数据进行滤波归一化等预处理；然后，将原始数据发送至簇首节点，簇首节点利用BP 神经网络的学习规则对数据进行融合处理，提取原始数据的特征信息并发送至Sink节点。簇成员节点和簇首节点通过BP 神经网络构造1个3层的神经网络模型。

2.2 IPSO优化BP神经网络步骤

具体实现步骤如下：

Step 1 初始化参数。粒子种群数目N，设置粒子速度变化范围［-vmin，vmax］，可搜索空间范围［-xmin，xmax］，最大迭代次数maxgen。设置惯性权重wmax，wmin和学习因子c1，c2，趋化行为增量因子λmax，λmin。确定BP 神经网络拓扑结构、初始化权值矩阵w1，w2和阈值矩阵b1，b2。

Step 2 把待优化的权值矩阵和阈值矩阵映射为粒子群的位置向量xi＝（w1，b1，w2，b2），设置粒子的速度向量vi＝（vi1，vi2，…，viD）。

Step 3 确定适应度函数。本文采用样本数据的均方根误差（RMSE）作为适应度函数

式中m为样本训练集大小，traini为训练样本数据融合预测值，yi为样本数据真实值。

Step 4 计算每个粒子的初始适应度值。记录粒子的个体极值Pbest，粒子群的全局极值Gbest。

Step 5 在Gbest更新时，根据式（5）选取T个粒子进行趋化操作，根据式（4）、式（6）更新粒子的趋化行为增量。

Step 6 根据式（7）、式（8）更新粒子速度和位置。

Step 7 根据式（12）计算σ2是否超过阈值来判断算法是否陷入局部最优，如果是，则按式（14）对粒子实施迁移操作，如果否，则执行步骤8。

Step 8 迭代控制。当达到精度要求或最大迭代次数时则进行下一步，否则返回Step 4 继续迭代搜索，并根据式（9）～式（11）分别更新w，c1，c2，λ。

Step 9 把全局极值Gbest映射为新的权值阈值矩阵w1，b1，w2，b2，作为BP神经网络的初始参数进行训练直至最优权值和阈值参数确定。

3 仿真实验与分析

实验仿真参数设置如下：网络规模为100 m×100 m，基站（BS）位置为（150，50）m，节点数量N为100，初始能量E0为0.5 J，功率放大能耗系数εfs为10 PJ／（bit·m2），发射电路损耗Eelec为50 nJ／bit，功率放大能耗系数εmp为0.0013 PJ／（bit·m4），簇首比例P为5%，融合数据能耗EDA为5 nJ／（bit·signal），数据包大小为200 bits。

本文以蒙特西尼奥公园的火灾面积数据集为研究样本，该数据集提供了500 多条火灾面积数据以及相应的温度、相对湿度、风速、降雨量等相关数据。本文的仿真实验中，设置BP神经网络为4输入1输出的单隐层结构。选取温度、相对湿度、风速、降雨量4项气象监测数据作为BP神经网络的输入参数，对应的火灾面积数据作为输出层参数，隐含层神经元的数量计算如下

式中n和l分别为输入层和输出层节点数，隐含层神经元数量取值范围为［4，12］，由表1 可以看出，在隐含层神经元数量为7时，均方根误差（root mean square error，RMSE）值最小，因此确定本文的神经网络为4-7-1的单隐层结构。

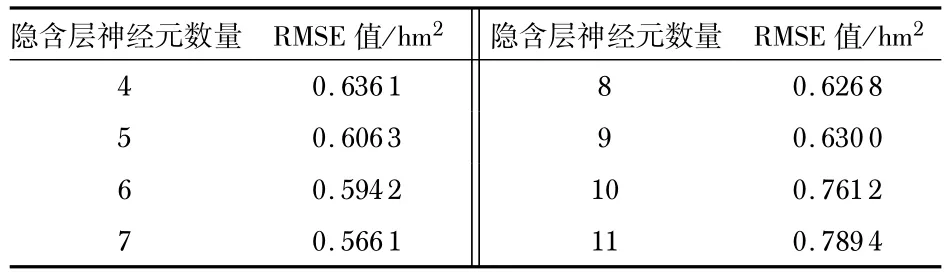
表1 隐含层神经元数量与RMSE值

3.1 融合精度

本文将通过平均相对误差（average relative error，AVRE）、RMSE以及拟合优度（goodness of fit，R2）3 种指标来评价算法的融合精度。图1为4种算法的数据融合结果对比，由图看出，IPSO-BP算法的融合结果与真实值更加接近，融合效果最好，相比于BP 算法和PSO-BP 算法融合精度更高。

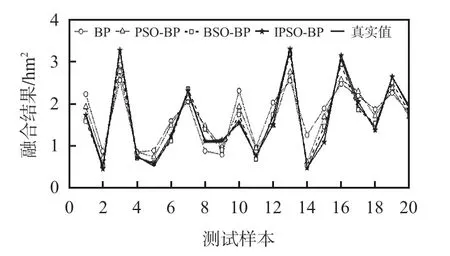
图1 4 种算法数据融合结果对比

表2为4种不同算法在AVRE、RMSE、R2的融合误差对比情况。IPSO-BP算法在3个评价指标方面明显优于其他3种算法。其中，IPSO-BP 较BSO-BP 算法相比，提升了19.15%的AVRE和12.18%的RMSE；而IPSO-BP与传统的BP算法相比，提升了31.48 %的AVRE 和33.56 %的RMSE；在R2方面IPSO算法较其他3种算法更接近于1，表明本文的模型性能更好。这在于IPSO算法中引入趋化算子增加了粒子的种群多样性，同时迁移算子的加入又解决了PSO算法的早熟收敛的问题，解决了传统BP 神经网络对初值参数敏感的缺陷，因此，IPSO-BP算法较3 种对比算法数据融合精度更好。

表2 融合误差对比

3.2 算法迭代收敛对比

图2为PSO-BP算法和BSO-BP 算法与本文算法的迭代收敛速度对比。由图可知，IPSO-BP 算法在整个迭代过程中收敛速度和寻优性能明显优于PSO-BP 算法和BSOBP算法。在训练迭代初期IPSO-BP 算法明显要优于其他2种算法，这是由于引入趋化算子丰富了粒子的搜索维度，增强了粒子群的局部寻优能力，但在迭代中期IPSO算法和BSO算法都陷入到了局部最优的情况，算法的适应度值较差，虽然BSO-BP 算法在26 代时其适应度值最好，但因为缺乏跳出最优的手段导致种群进化停滞不前，而IPSO-BP算法在45代左右因为迁移算子的加入使得种群跳出局部最优解，并在50代时算法收敛至全局最优解附近，且适应度值比BSO-BP算法更低，因此，本文算法较其他算法收敛速度更快，能更好的优化BP神经网络。

图2 算法迭代收敛对比

3.3 网络生命周期对比

图3为3种算法的网络生命周期对比，由图可以看出，当网络存活节点低于85%的阈值［13］时，LEACH算法运行到700轮左右，而本文算法和BP算法则运行至850轮时左右，比LEACH算法增加了21.43%的网络生命周期。

图3 存活节点个数对比

4 结 论

通过在粒子群中引入BAO 算法的趋化算子和迁徙算子来改进粒子群局部寻优能力差和易陷入局部最优解的缺陷；然后利用IPSO 算法优化BP 神经网络的权值和阈值；引入到WSNs数据融合中，簇首节点通过优化后的BP神经网络对采集数据进行融合处理；将少量代表原始数据的特征信息发送至Sink节点。实验表明：本文算法能有效提高融合精度和收敛速度，降低冗余数据传输能耗，延长网络生命周期。