对弹簧的形变量超出弹性限度后F-x图像的讨论

陈 俊

(南京市第九中学,江苏南京 210018)

1 问题的提出

“探究弹簧弹力与形变量的关系”是新人教版教材必修1第3章的学生实验,也是2017年版《普通高中物理课程标准》中要求的21个学生必做实验之一,旨在让学生通过自己的探究找到弹簧弹力与形变量之间的关系,得出胡克定律.

在实验操作过程中,一般要求在实验中将弹簧的长度控制在弹性限度之内,以保证实验的效果.什么是弹性限度?弹性限度是指当弹簧受到外力作用,且在其内部所产生的抵抗外力不超过某一极限值时,撤去外力,其形变可以全部消失,弹簧完全恢复到原状态,这个极限值称为“弹性限度”.一旦弹簧超过其弹性限度,在撤去外力后,弹簧不能完全恢复到原来形状,此时弹簧被损坏了.

弹簧的形变量超过弹性限度后,弹力与形变量究竟存在怎样的关系在实验中很少涉及,在试题的命制中也基本上回避这个问题.如果命制试题时涉及到这个问题,因为缺少相关的理论和实验的支持,往往出题者按照自己的想象给出答案,就会出现不同的解答.

例1.小华做“探究弹力和弹簧伸长量的关系”的实验.

(1)图1(甲)是不挂钩码时弹簧下端指针所指的标尺刻度,其示数为7.73 cm;图1(乙)是在弹簧下端悬挂钩码后指针所指的标尺刻度,此时弹簧的伸长量ΔL为_________cm.

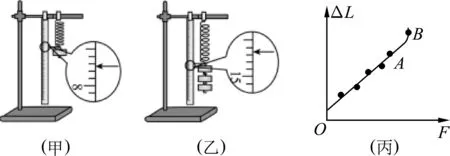
图1

(2)图1(丙)是该同学描绘的弹簧的伸长量ΔL与弹力F的关系图线,

①图线未过坐标原点,造成这种现象的主要原因是_______________________________________.

②图线的AB段明显偏离直线OA,造成这种现象的主要原因是____________________________.

例2.用如图2(甲)所示的装置做“探究弹簧弹力F与弹簧伸长量x的关系”实验,将弹簧竖直悬挂,装置静止时,近似认为下端所挂钩码的重力大小等于弹簧弹力F大小.

图2

在没有操作失误的情况下,某小组通过该实验得到多组弹簧弹力F与弹簧伸长量x的数据,根据数据画出F-x的图像如图2(乙)所示,出现这种现象的原因是___________________________.

从试题的设问来看,都涉及到了弹簧的形变量超过弹性限度后弹力随形变量的变化趋势,但是却出现了两种截然相反的设问.

那么在弹簧的长度超过弹性限度后,弹力与形变量之间究竟存在怎样的关系呢?

2 实验探究

实验是探究物理规律的手段之一.通过实验可以直观地将几个物理量之间的关系呈现出来,所以接下来通过实验来探究弹簧的长度超过弹性限度后,弹力与形变量之间的关系.

传统的实验室利用弹簧和测力计来完成探究过程.随着社会的发展,科技的进步,信息技术越来越多地被应用到物理实验中.在2017年版《普通高中物理课程标准》中明确提到:“要重视数字实验,创新实验方式.”数字实验室系统是利用传感器、数据采集器等收集实验数据,用计算机软件分析实验数据、得出实验结果的现代化实验系统.数字实验系统是教育信息化发展的需要,更是学生创新能力培养的重要方法和手段.利用数字实验系统可使很多难以测量或难以控制的实验得以顺利进行,也使很多实验的测量精度大大提升.

本次探究运用了无线智能小车来进行(如图3所示),配合相关的软件“SPARKvue”,可以实时描绘出弹簧中的弹力(纵坐标)与形变量(横坐标)之间的图像(如图4所示).

图3

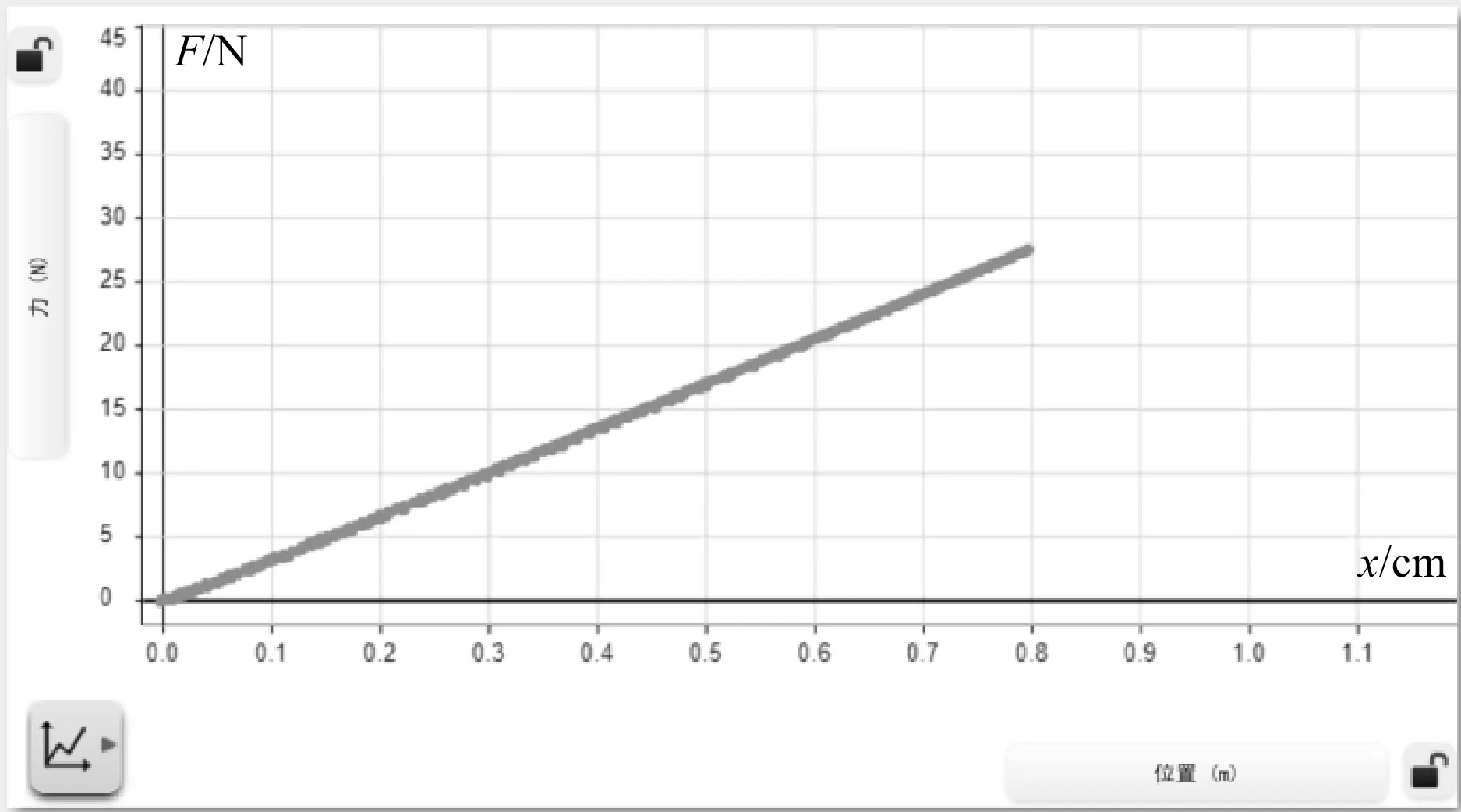
图4

(1)第1次实验.

实验器材:一根原长为12.7 cm,外径2.52 cm,线径1.4 mm的弹簧(如图5所示),无线功能小车,电脑及相关软件.

图5

第1次操作:使弹簧形变量在弹性限度内,改变弹簧的长度,使得弹簧的形变量在80 cm以内变化.通过无线功能小车得出弹簧中的弹力与形变量之间的关系,得出相应的F-x图像(如图6所示).从图中可以看出F-x图像是一条过原点的直线,图线的斜率反映了弹簧的劲度系数,说明在弹性限度内弹簧中的弹力与形变量之间很好地遵循了胡克定律,且从图中可以求出劲度系数k=35 N/m.

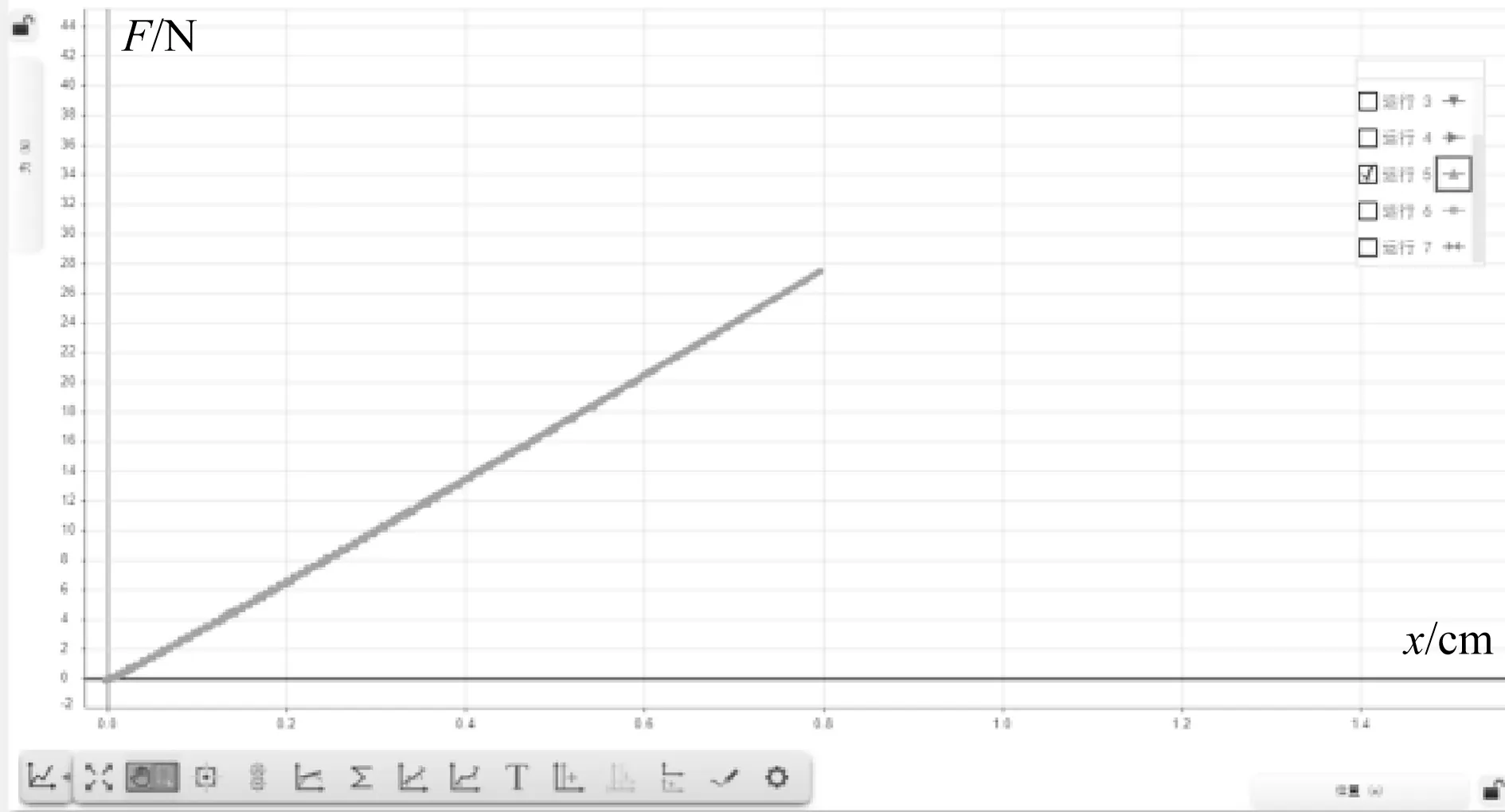
图6

第2次操作:使弹簧在超出弹性限度后,研究弹力与弹簧的形变量之间的关系.

弹簧的原长为12.7 cm,用力拉弹簧使弹簧的长度超过150 cm,很明显这个形变量应该超出了弹簧的弹性限度.撤去拉力后发现弹簧的长度变为44.1 cm(如图7所示),亦说明本次实验中弹簧的形变量超出了弹簧的弹性限度.

图7

通过无线智能小车,得出相应的F-x图像(如图8所示).

图8

从图8中可以看出:在拉伸过程中,弹簧的形变量大约在100 cm以内,F-x的图线是一条直线,表明弹簧中的弹力与形变量之间基本上能遵循胡克定律.形变量在100 cm～150 cm之间,F-x的图线向下发生弯曲,斜率逐渐变小,表示在这段距离内弹簧的劲度系数逐渐变小,此时弹簧的形变量应该是超过了弹性限度.

在收缩过程中,F-x的图线是一条平滑的曲线,表明当弹簧的形变量超过弹性限度后,弹簧的劲度系数不再是一个定值,这根弹簧基本上被破坏了.

一次实验可能具有偶然性,下面换一根不同的弹簧来重复刚才的步骤,对两次实验进行比较,看一下能得出怎样的结果.

(2)第2次实验.

实验器材:一根原长为10.0 cm,外径1.93 cm,线径1.0 mm的弹簧(如图9所示).

图9

第1次操作:在弹性限度内改变弹簧的形变量,得到F-x图像(如图10所示).可以看出:在弹性限度内,F-x图像中的图线是一条过原点的直线,说明弹簧中的弹力与弹簧的形变量之间遵循胡克定律,且从图中可以求出劲度系数k=15 N/m.

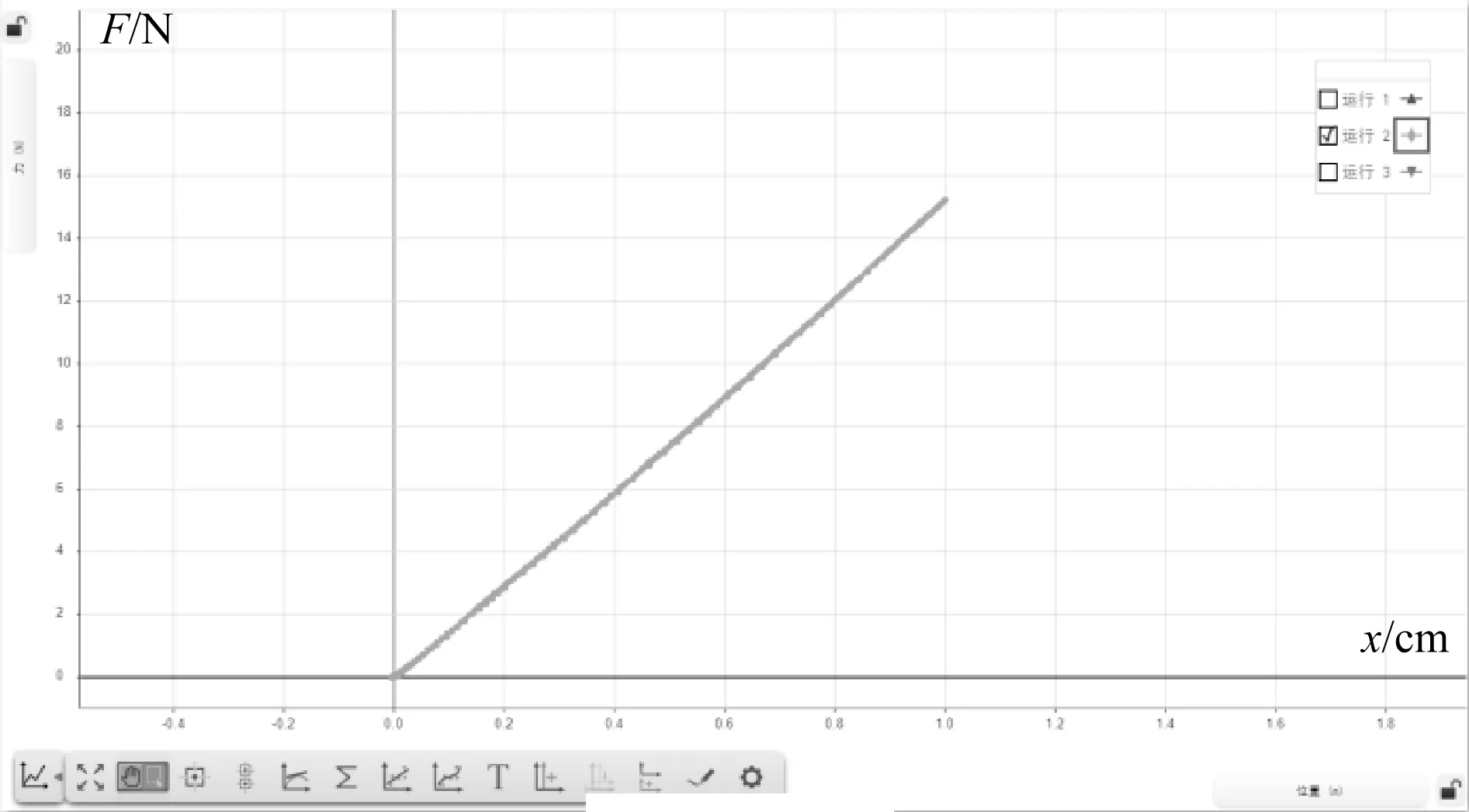
图10

第2次操作:使弹簧在超出弹性限度后,弹簧的原长为10.0 cm,用力拉弹簧使弹簧的长度超过150 cm,很明显这个形变量应该超出了弹簧的弹性限度;撤去拉力后发现弹簧的长度变为28.3 cm(如图11所示),亦说明本次实验中弹簧的形变量超出了弹簧的弹性限度.

图11

通过无线智能小车,得出相应的F-x图像(如图12所示).

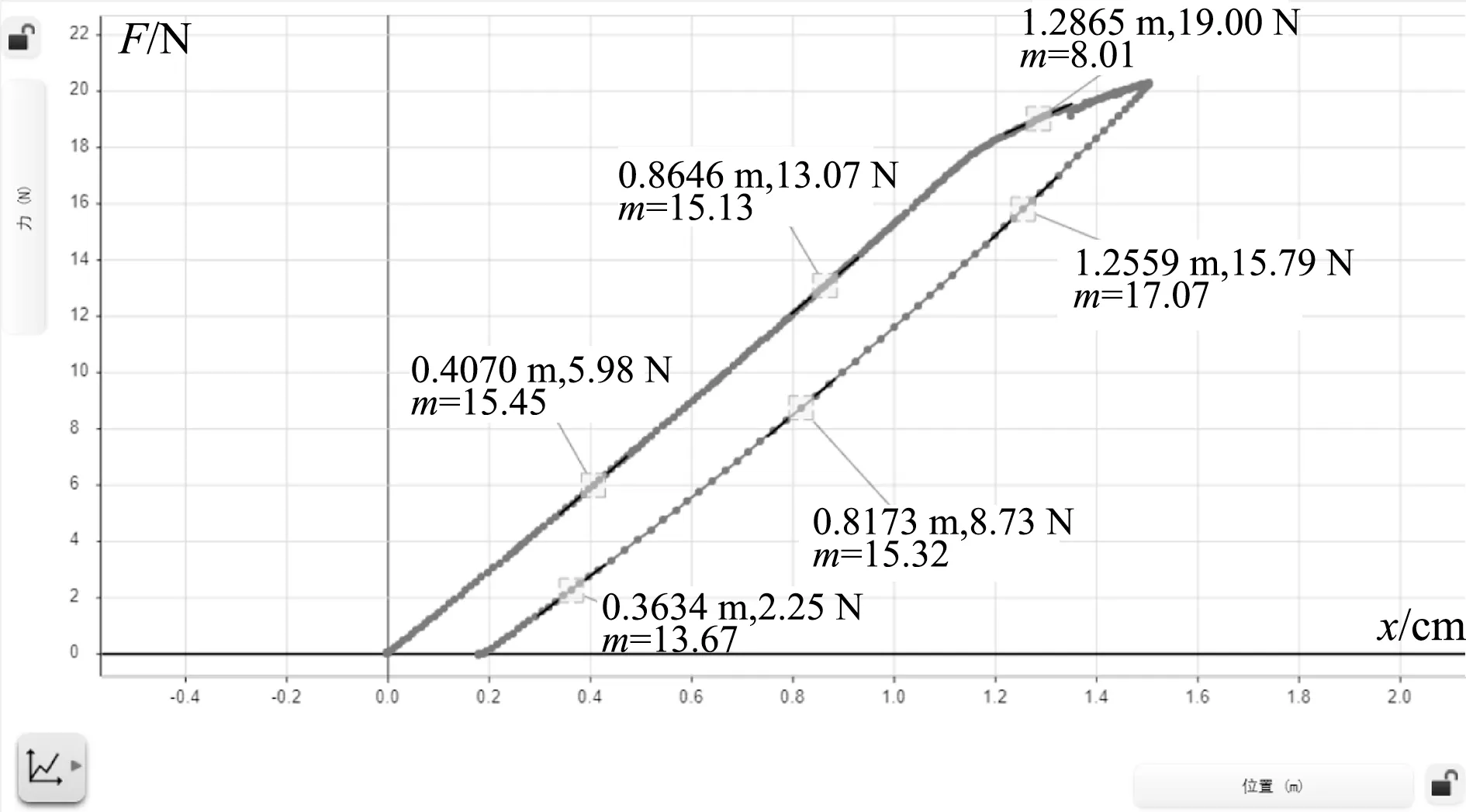
图12

从图12中可以看出:弹簧的形变量超过了一定长度后,F-x的图线向下发生弯曲,斜率逐渐变小,表示在这段距离内弹簧的劲度系数逐渐变小.

通过两次实验可以看出:当弹簧的形变量在弹性限度内时,弹簧的弹力与形变量之间遵循胡克定律.当弹簧的形变量超过弹性限度后,弹簧中的弹力与形变量不再满足胡克定律,其F-x图线将发生弯曲,在一定范围内弹簧的劲度系数将逐渐变小.

同样在收缩过程中,F-x的图线是一条平滑的曲线,表明当弹簧的形变量超过弹性限度后,弹簧的劲度系数不再是一个定值,这根弹簧基本上被破坏了.

从上述结论可以看出:例1中第(2)问中②的设问符合实验结果,而例2中的设问跟实验结果不吻合.

3 原因初探

(1)为什么当弹簧的形变量超过弹性限度后,弹簧的劲度系数将逐渐变小?

笔者通过分析,初步认为,在弹簧拉伸过程中将经历以下几个阶段.

①在弹簧的形变量较小时,弹簧处于弹性变形阶段,弹簧要恢复到原来的形状,所以将产生抵抗外界的力,这个抵抗力将随着形变量的增加呈线性增加.

②当弹簧的形变量超过一定量后,弹簧处于微塑形应变阶段.在这个阶段内已经不能完全恢复到原来的形状了,弹簧抵抗外力的效果反而会有所降低,表现为在这个阶段的劲度系数将减小.

③继续增大拉力,弹簧可能将达到一个屈服点,超过这个限度后,撤去外力,弹簧的长度不会出现恢复的状况了.

(2)其他弹性绳会不会出现这样的现象呢?

在中学阶段满足胡克定律的模型不仅仅是弹簧,一般认为弹性绳都同样满足胡克定律,最典型的弹性绳是橡皮筋,在“探究合力与分力之间的关系”实验中,就是利用了橡皮筋的长度相同,橡皮筋中的弹力也相同的结论来完成实验探究过程的.

那么橡皮筋中的弹力与橡皮筋的形变量之间存在怎样的关系呢?当橡皮筋形变量超过弹性限度后,其Fx的图线变化趋势跟弹簧呈现出同样的规律吗?

利用无线智能小车得出橡皮筋中的弹力与形变量之间的图像(如图13所示).

从图13中可以看出:严格意义上讲,橡皮筋的弹力与形变量之间并不符合胡克定律,因为拉升过程中与收缩过程中经过同一位置时,橡皮筋中的拉力不相等.当然在新的橡皮筋在形变量较小时,可以认为弹力与形变量之间基本上符合线性变化的关系;当橡皮筋的形变量较大时,将橡皮筋拉伸到几乎不能再拉动的情况下,从图中可以看出橡皮筋中的拉力将急剧增加,Fx的图线将向上发生弯曲,这可能也是上述例2设问的一个依据.