从物像等光程性探讨光成像规律及其推广应用
王 勇
(江苏省常州高级中学,江苏常州 213003)
几何光学中成像规律研究基于3个基本实验定律:(1)光在均匀的介质中直线传播定律;(2)光通过两种介质分界面时的反射定律和折射定律;(3)光的独立传播定律和光路可逆原理.在已有的文献中绝大多数都是基于反射和折射定律推导近轴光线传播和球面折射成像规律.本文将从波动光学的角度基于费马原理中的物像间等光程分析光线传播问题和球面折射成像规律,并将球面折射成像规律推广到平面折射成像规律、球面反射和平面反射成像规律;基于物像之间的光程特点分析物理竞赛中一些特殊的光学成像系统.
费马原理可以表述为:光线沿光程为平稳值的路径而传播.当光在指定的两点之间存在多条路径时,若某条光线光程是极小或极大,则意味着其邻近光线光程不处于平稳值,这违背费马原理,所以物像之间光程只能是相等的.
1 物像等光程性推导成像规律
1.1 反射定律的推导
如图1所示,两平行光从无穷远处入射到分界面,反射光也为两条平行光,两虚线O1A、O2B为等光程面,在两等光程面O1A和O2B之间光程O2A=O1B,则两直角三角形△O1AO2与△O2BO1全等.全等直角三角形中两直角边O1A=O2B,根据直角边与斜边关系有O1O2cosθ1=O1O2cosθ2,所以反射角与入射角相等.

图1
1.2 折射定律的推导
如图2所示,两平行光从无穷远处射到分界面发生折射,O1A、O2B为等光程面,在光程面O1A和O2B之间光程相同,所以有n1AO2+0=0+n2O1B,在两直角三角形中有AO2=O2O1sinθ1,O1B=O2O1sinθ2,将AO2、O1B代入,有n1sinθ1=n2sinθ2.

图2
1.3 球面折射成像规律推导
1.3.1 物距与像距关系
如图3所示,处于主光轴上的物点A经球面成像于主光轴的另一侧像点B,球面两侧的折射率分别为n1、n2,主光轴与球面的交点为O,球面球心为C,若物距AO长s,像距BO长s',球的半径为r,MC与主光轴的夹角为θ,由物像等光程性有n1AO+n2OB=n1AM+n2MB,则有

图3
对于近轴光线θ→0,则有化简后有
当θ→0时作泰勒展开后,化简可得
对于任意θ小角都成立,则有
化简后有球面折射成像物距与像距关系
1.3.2 物高与像高关系
将主光轴绕圆心C旋转一小角度,形成如图4所示一虚线副光轴,物点与像点绕圆心C转动后物点与像点的弧线长度近似为物高和像高,若物高为y,像高为y',则有
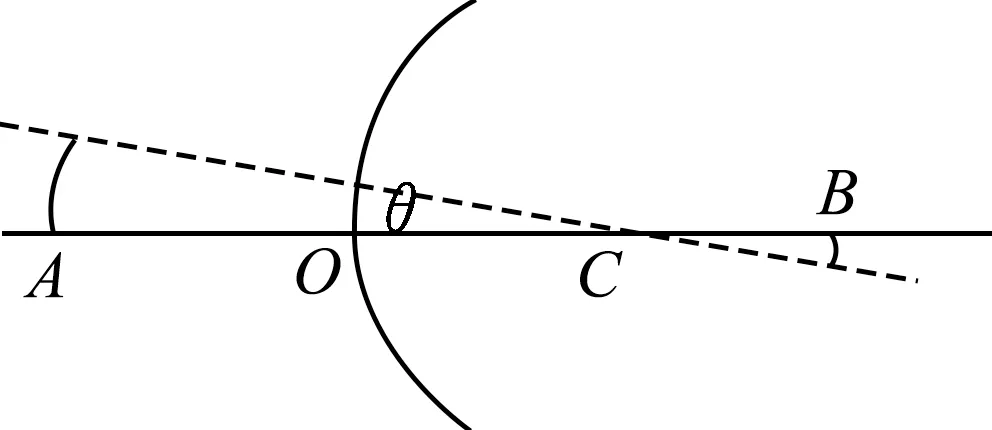
图4
将式(1)代入可得
若规定主光轴上方物高与像高为正,主光轴下方物高与像高为负,考虑物高与像高的符号,则得物高与像高关系为
1.3.3 折射成像规律的推广
当为平面折射成像时,平面曲率半径r→∞,有,只要代入式(1)就可得平面折射成像的物距与像距关系式,化简后物距与像距关系为
当研究平面镜的反射成像规律时,不同光线物像之间的路程不同,若要保持物像之间等光程,则平面镜成像后物像之间的光程和必为0.当入射光线一侧的光程为nl时,平面镜另一侧光线光程必为虚光程,虚光程为-nl,平面镜另一侧的折射率可等效为-n.
当为球面反射成像时,可认为球面镜另一侧的折射率可等效为-n,只要代入式(1)就可得球面反射成像规律为,化简后可得球面反射物距与像距的关系为.球面折射成像的像方在入射光线的另一侧,但球面反射成像的像方在入射光线的同侧,所以球面反射中的s'<0表示球面反射成实像,球面反射中的s'>0表示球面反射成虚像.为了统一像距为负值时成虚像这一约定,可将球面反射物距与像距的关系改写为,其中-s'为球面反射的像距.
若设-s'=s″,球面反射物距与像距的关系为
当为平面反射成像时,平面曲率半径r→∞,有,只要代入式(3)就可得平面反射成像的物距与像距关系式,化简后关系为s″=-s.
2 竞赛中应用
2.1 物像等光程在负折射率竞赛题中应用
例1.(第35届物理竞赛决赛题)介质的折射率n可以大于0,也可以小于0,n小于0的介质称为负折射介质.光在负折射介质内传播,其光程为负值(相位随传播距离的变化规律与在折射率为正的介质中的相反).如果定义折射角与入射角在界面法线同侧时折射角为负,可以证明折射定律在界面两边有负折射介质时仍然成立,即n1sinθ1=n2sinθ2,其中n1和n2均可以大于0或小于0.
(1)设想一束平行光入射到界面上,在答题纸上画出图5(a)和图5(b)所示情况下进入介质2的光线及对应的子波的示意图,并依此证明折射定律成立.

图5
(2)如图5(c)所示,半径为R的球面将空间隔开为两个区域,其折射率分别记为n1(n1>0)和n2(n2<0)C点是球面的球心,图中已画取某一光轴与球面的交点O为原点.图中已画出此情形下一段入射光线和折射光线,x和y分别为入射光线、折射光线与光轴的交点坐标.记物距为s1,像距为s2.在傍轴近似下导出球面的成像公式和横向放大率公式.请明确指出最后结果中各个量的正负号约定.
(3)设介质1为空气,即n1≈1,n2可大于0也可小于0.在球面[参考图5(c)]前放置一普通薄凸透镜,透镜的光轴通过球心C,焦点位于负折射介质区域内,透镜的焦距f=1.5R,透镜中心O'点与O点的距离为d.一束沿光轴传播的平行光入射到薄透镜.分别就表中4组参数计算入射光在光轴上会聚点离O点的距离,并在答题纸上画4组参数计算入射光在光轴上会聚点离O点的距离,并在答题纸上画4情形的光路示意图.
解析:(1)图5(a)中两边介质都是正折射率,证明和作图如上.对于负折射率介质中成像问题可类比光的折射定律、折射成像规律推导.若光线在负折射率介质一侧折射到法线的另一侧时,光从正折射率一侧到负折射率一侧时,两等光程面之间的两条光线的光程一正一负,光程差不可能相等,折射光线只能偏折到法线的同侧才能保证两等光程面之间光程相等,且两等光程面间光程为0.即n1AO2+n2O2B=0,光的折射如图6所示,由于AO2=O1O2sinθ1,O2B=-O1O2sinθ2,负号由于θ2<0,代入可得n1O1O2sinθ1-n2O1O2sinθ2=0,化简后可得n1sinθ1=n2sinθ2.
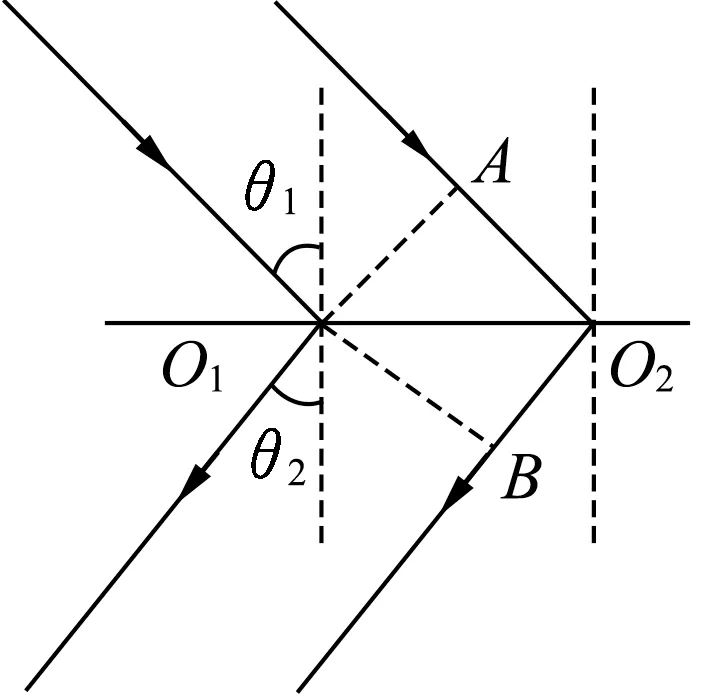
图6
(2)如图7所示,当在负折射率介质中球面折射时,根据物像间等光程,有n1AO+n2OB=n1AM+n2MB,化简后同样有

图7
(3)略.
2.2 物像等光程性在透镜成像中的应用
例2.(第38届物理竞赛复赛题)(1)如图8所示,一宽束平行光正入射到折射率为n的平凸透镜左侧平面上,会聚于透镜主轴上的点F,系统过主轴的截面如图8所示.已知凸透镜顶点O到F点的距离为r0.试在极坐标系中求所示平凸透镜的凸面形状,并表示成直角坐标系中的标准形式.
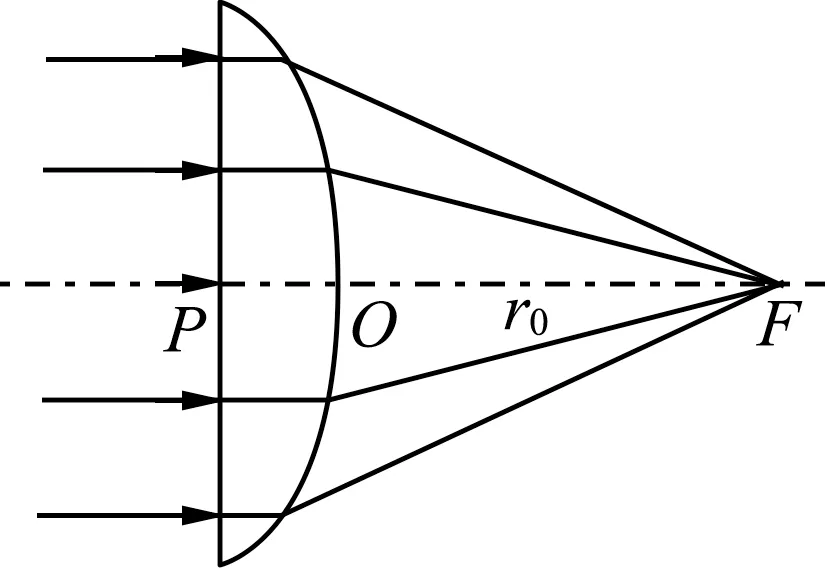
图8
(2)在如图8所示的光学系统中,共轴地插入一个折射率为n'的平凹透镜(平凹透镜的平面在凹面的右侧,顶点在O、F点之间的光轴上,到F的距离为r0',r0'<r0),使原来汇聚到F点的光线经平凹透镜的凹面折射后平行向右射出.
①在极坐标系中求所插入的平凹透镜的凹面形状,并表示成直角坐标系中的标准形式;
②已知通过平凸透镜后的汇聚光线与主轴的夹角θ的最大值为θmax,求入射平行圆光束与出射平行圆光束的横截面半径之比.
解析:(1)平行光正入射到平凸透镜左侧平面上后聚焦到主光轴上的F点,无穷远处的物与像点F之间等光程,由于平凸透镜左侧为平行光,则如图9所示,虚线为等光程面.虚线到像点F的光程相等,则有MF=nHO+OF,当以聚焦点F为极点建立极坐标系,若极径MF为r,极角为θ,则有r=n(rcosθ-r0)+r0,化简后可得r=当以主光轴为x轴,垂直于主光轴过F点的直线为y轴时,可得在直角坐标系中的凸面形状方程为
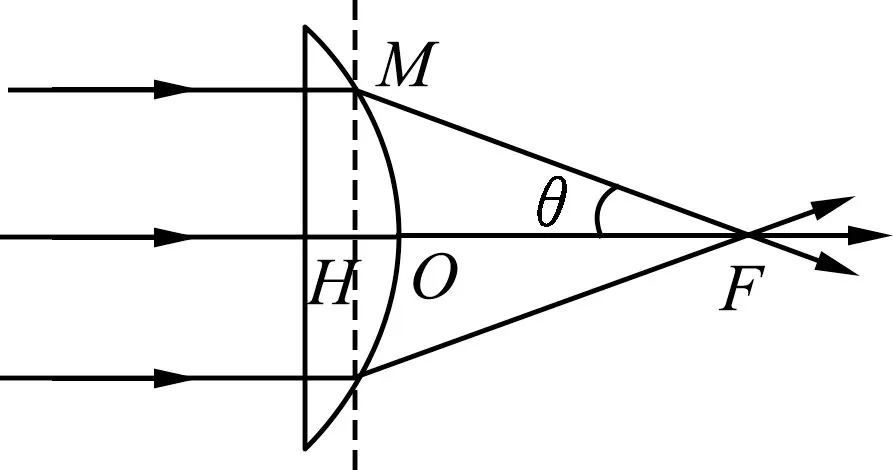
图9
(2)①如图10所示,当聚焦光线进入一折射率为n'的平凹透镜,使原来汇聚到F点的光线经凹面折射后平行射出,在平凹透镜内的虚光线对应为虚光程,在虚物与N'F平面间光线等光程,有-FM'+n'M'N'=-FO'+n'O'F.当以F为极坐标的极点时有-r+n'rcosθ=-r0'+n'r0',化简后可得当以主光轴为x轴,垂直于主光轴过F点的直线为y轴时,可得在直角坐标系中的凸面形状方程为

图10
②解略.
3 物像等光程性的推广应用
例3.(第30届物理竞赛复赛题)一斜劈形透明介质劈尖,尖角为θ,高为h.今以尖角顶点为坐标原点,建立坐标系如图11所示;劈尖斜面实际上是由一系列微小台阶组成的,在图11中看来,每一个小台阶的前侧面与xz平面平行,上表面与yz平面平行.劈尖介质的折射率n随x而变化,n(x)=1+bx其中常数b>0.一束波长为λ的单色平行光沿x轴正方向照射劈尖;劈尖后放置一薄凸透镜,在劈尖与薄凸透镜之间放一挡板,在挡板上刻有一系列与z方向平行、沿y方向排列的透光狭缝,如图12所示,入射光的波面(即与平行入射光线垂直的平面)、劈尖底面、挡板平面都与x轴垂直,透镜主光轴为x轴.要求通过各狭缝的透射光彼此在透镜焦点处得到加强而形成亮纹.已知第一条狭缝位于y=0处;物和像之间各光线的光程相等.

图11

图12
(1)求其余各狭缝的y坐标;
(2)试说明各狭缝彼此等距排列能否仍然满足上述要求.
解析:(1)如图12所示,斜劈直角边左侧的平行光等光程.通过透光狭缝后的平行光经过凸透镜成像于焦点,斜劈虚线右侧平行光到焦点的光线也是等光程.当要使全部平行光聚焦到焦点处得到加强而形成亮纹,所以斜劈直角边与虚线间的光程理应相等,但由于斜劈介质的折射率n随x而变化,斜劈直角边到虚线间距离又相等,所以斜劈直角边到虚线间的光程不可能相等.因此若要使全部平行光聚焦到焦点得到加强而形成亮纹,只能斜劈直角边到虚线间相邻透光狭缝位置处的光程差为波长的整数倍,才能确保所有平行光到焦点时振动同步.
射到斜劈y处的光线,光程为
y处通过非斜劈部分的光程δ2(y)=hytanθ,斜劈y处的直角边与虚线间的光程为以上两光程和δ(y)=δ1(y)+δ2(y)=
由于位于y=0处无介质光程为h,斜劈y处与O处的光程差为
当斜劈y处与y=0处的光程差满足时(k=1,2,3…),通过各狭缝的透射光将在透镜焦点处振动同步而得到加强的亮纹.
综上所述,本文基于费马原理中物像间的等光程性从理论上推导出光的反射定律、折射定律、球面折射成像规律,从波动角度进一步认识了光的成像本质.当前物理竞赛中光学竞赛题也正在由纯几何光学逐步向特殊光学元件研究设计和光学仪器的原理考查转变,如波带片、迈克尔逊干涉仪等,从波动角度利用光程分析也是解决光学竞赛题的一大利器.
——可看得见的权利

