复杂基坑支撑结构监测点布置优化

姚冠华,张 翾,张 鹏,3,王礼华,史豪杰

(1.南京工业大学 交通运输工程学院,江苏 南京 211800;2.交通运输部公路科学研究院,北京 100088;3.南京智慧岩土工程技术研究院,江苏 南京 211800;4.中交一公局第四工程有限公司,广西 南宁 530219)

随着我国城市地下空间的开发力度越来越大,复杂深大基坑工程越来越频繁出现[1-2]。随之而来,基坑工程施工安全风险日益突出,这对基坑工程健康监测的准确性和可靠性提出了更高要求[3]。传统基坑支护结构监测点常采用对称、均匀、等距布置方式,这显然只适用于结构受力体系简单的中小型基坑工程,然而对于复杂深大基坑,由于支撑体系的复杂性,土压力与开挖区块的非对称性,使得基坑支撑结构处于动态调整变化受力过程,这就要求提高基坑支撑结构监测点布置的合理性与科学性。

近年来,基坑监测技术迅猛发展,在传感器选取、信息传输格式、监测系统与监测信息分析方法方面均取得了较多成果[4-5]。在传感器方面,朱瑞喜等[6]基于Flex技术制备了一种大位移传感器,可用于土体内部大位移的实时监测;索文斌等[7]和Zheng等[8]将分布式光纤技术应用于深基坑支护桩和边坡的变形监测,有效获取了深基坑支护桩和边坡的变形信息。在信息传输格式方面,何宏盛等[9]采用基于电气与电子工程师协会(IEEE)批准通过的 802.15.4 无线标准Zig Bee无线传输技术,开发了深大基坑无线自动化监测系统。在监测系统方面,徐杨青等[10]采用C语言和SQL server数据库,并结合监测手段和专业技术,开发了一套基坑监测预警系统;隋海波等[11]设计了一套基于布里渊光时域反射技术(BOTDR)的新型基坑工程分布式监测系统;赵峰[12]开发了一套基于建筑信息模型(BIM)的基坑工程自动化监测系统以及管理平台;郑世杰等[13]采用Revit软件构建了基坑的三维模型,并对基坑采用自动化监测系统,通过无线传输监测数据,并结合C语言编译了数据管理系统;高磊等[14]利用地理信息系统(GIS)和数据库技术对监测信息进行信息化管理。在监测信息分析方面,李思慧等[15]和Ji等[16]基于最小二乘支持向量机(LSSVM)模型和实际的监测数据构建基坑变形时间序列预测方法。在监测点优化布置方面,黄晓程等[17]统计分析两个深大基坑的监测曲线规律,提出了大型深基坑施工内控集约化监测点布设方法;杜云等[18]依据风险评估理论,讨论基坑风险评估与监测点优化之间的关系,提出了基于高风险源的基坑监测点布置优化方法;王克等[19]根据现场实际工程监测经验及监测数据分析处理结果,提出基坑监测点布置的优化原则,大多数人对于基坑监测点的布置优化问题只给出关于优化的指导性建议,没有实现对监测点的精确优化布置。

本文提出了一种融合模态分析与粒子群算法的复杂基坑支撑结构监测点布置优化方法,该方法聚焦于基坑支撑结构的监测点优化问题,监测内容为支撑结构的水平位移和竖向位移。首先,介绍优化方法技术路线;其次,详细给出基于模态参数的位移模态适应度函数构建方法与优化判别标准;而后,交代了粒子群优化算法搜索步骤;最后,依托南京江北新区某基坑为案例,验证了所提方法的优越性。

1 基坑支撑监测点布置优化方法

提出的基坑复杂支撑体系监测点布置优化方法的技术路线如图1所示。由图1可知:路线共分为两大步,结构模态分析和粒子群优化算法。

图1 基坑支撑监测点布置优化技术路线Fig.1 Optimized technical route for the layout of foundation pit support monitoring points

首先,利用ANSYS有限元软件对结构进行模态计算;然后,根据获取的模态参数,计算基于模态置信度准则(MAC法)的适应度函数粒子群算法中粒子的适应度;最后,利用粒子群优化算法不断地迭代计算更新粒子的位置和速度,最终适应度曲线趋于收敛,则认定此时最优粒子所处位置为监测点最优布置方案。

2 模态分析方法

模态分析方法是结构动力学的一种分析方法,已经被广泛地应用在桥梁和大跨度空间结构的健康监测中[20-22]。模态分析包括数值模态分析和试验模态分析,本文采用ANSYS软件进行数值模态求解。

对于复杂支撑体系,假定支撑结构为无阻尼震动,建立模态分析系统方程式(1),得到其模型的模态振型。

(1)

式中:K为刚度矩阵,φi为第i阶模态的振型向量,ωi为第i阶模态的固有频率,M为质量矩阵。

首先,将大跨度基坑的围护结构进行简化,大跨度基坑的支撑体系结构可以用梁单元代替,建立大跨度基坑复杂支撑体系结构的有限元分析模型;然后,对模型施加约束,选择想要获得的模态阶数,选取Block Lanczos法[23]进行模态提取;最后,对结果进行后处理,获取模态振型数据,并对数据进行预处理。

3 基于MAC法的适应度函数

建立关于模态振型的评价函数,根据结构动力学可知,结构节点处的各固有振型之间是一组相互正交的向量。受监测能力的制约,实际测量的自由度数量远远少于结构模型的自由度数量,加上测量过程中仪器的误差和测量噪音的影响,实测得到的模态向量往往已经失去了正交性,甚至在一些情况下会丢失模型重要的模态信息,这往往是由于向量间空间交角过小所导致的,因此在选择监测点时应优先选择模态向量交角较大的点,从而把结构的特性最大化保留下来,Kammer[24]提出的有效独立(EI)法,实际上就是围绕这一思路所展开的。Carne等[25]发现MAC矩阵可用于评价模态向量空间交角,MAC矩阵具有简单、高效的特点。

模态置信度公式为

(2)

式中:Φi为第i阶模态振型向量,Φj为第j阶模态振型向量,Cij为Φi和Φj之间交角的余弦值,其值范围为0～1。

当Cij为0时,表示Φi和Φj之间的正交性最优,两振型向量之间线性无关;当Cij为1时,则表示Φi和Φj之间正交性最差,振型向量之间线性相关。为了提高测点之间的有效性,就应该使监测点之间的MAC矩阵非对角元的最大值尽可能小,即使所要优化的目标函数最小。为了方便计算,适应度函数为

f(x)=max{Cij}i≠j

(3)

f1=1-f(x)

(4)

式中:f(x)为目标函数最大值;f1为1与目标函数最大值的差。

由上式可得,利用MAC矩阵的特点,将求解目标函数最小值成功转化为了求解目标函数最大值的问题,f1越接近1,说明优化效果越好。

4 粒子群算法求解

4.1 粒子群算法

粒子群算法是仿生优化算法的一种,它是通过模拟简化的鸟群捕食行为社会模型所得出的优化算法,由Kenndy等[26]提出,通过模拟鸟类个体在捕食过程中的合作与竞争,实现对全局最优结果的搜索,按照需求随机产生的一组解被称为粒子。通过已有的粒子在限定空间内随机的运动,不断迭代从而找寻到最优的结果。粒子在迭代的过程中不断随最优粒子进行搜索,粒子群算法具有简单易懂、容易实现,并且没有大量参数需要调整的优点,目前已经被广泛地应用在各个领域[27-29],其中土木工程中粒子群优化算法的应用也越来越多。

粒子群算法需要随机初始化粒子群,确定粒子的初始速度和位置,得到每个粒子在可行解空间里的随机解,让每个粒子从随机解出发,所有粒子在每次迭代中基于两个极值来更新自己的速度和位置,一个是单个粒子本身在飞行过程中经历过的最好位置,即自己在当前可行解空间中搜索到的最优位置,称为粒子的个体极值,用pid表示;另一个极值是粒子群体中所有粒子经历过的最好位置,即整个种群搜索到的最优解,称为粒子群的全局极值,用pgd表示。为了避免粒子群算法出现局部收敛的状况,将惯性权重(ω)引入粒子群算法中,整个粒子群的速度和位置的更新公式为

(5)

(6)

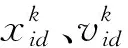
4.2 粒子群算法实现流程

第1步,初始化粒子群,设置粒子群的规模,种群规模大小一般为30～50;

第2步,设置单个粒子的维数(d),维数为布置监测点的数量;

第3步,设置单个粒子的位置范围[-xmax,xmax],其中xmax为粒子的最大位置,粒子取值范围与实际优化问题的参数有关;

第4步,设置单个粒子的速度范围[-vmax,vmax],其中vmax为粒子的最大速度,通常设定vmax=kxmax,其中k为常数,通常取值为0.1≤k≤1;

第5步,设置单个粒子的加速常数c1和c2;

第6步,设置惯性权重(ω),惯性权重使单个粒子保持运动惯性,使其有扩展和探索空间的趋势;

第7步,设置算法的最大迭代次数,最大迭代次数与计算模型的复杂度有关;

第8步,设置单个粒子的初始位置和初始速度,初始位置xtd为粒子t在d维的位置,xtd=2xmaxRand(*)-xmax,初始速度vtd为粒子t在d维的速度,vtd=2vmaxRand(*)-vmax,其中,Rand(*)为[0,1]均匀分布的随机数产生函数;

第9步,适应度计算,将初始化完成后的粒子代入到适应度函数中,计算粒子的适应度;

第10步,比较每个粒子的适应度,每个粒子找到的个体在历史上最优的位置信息为个体极值ptd,ptd为粒子t在d维上出现的历史最大值,这些个体历史最优解中的最大值为全局最优解,将其与历史全局最优解比较,选出较大的作为当前的历史最优解pgd,pgd为粒子群g在d维上出现过的历史最大值;

第11步,根据式(5)和(6)更新粒子的位置和速度;

第12步,若达到设置最大迭代次数,则结束;否则,从第9步循环。

5 工程实例

5.1 建模与求解

以南京江北新区某大型圆形基坑为例,应用所提出的复杂支撑监测点布置优化方法进行监测。该基坑位于南京江北新区核心区,距基坑东北侧约200 m处有一在建居民小区,以高层建筑为主,基础形式为桩基础,基坑西侧紧邻城市快速路,每天有大量车辆通行。该基坑场地条件较好,但考虑到车辆通行所产生的动力荷载会对基坑产生一定的影响,以模态分析为基础的监测点优化布置方法非常适用于该类基坑。基坑长150 m、宽132 m、埋深19.5 m,基坑内部设置4道临时钢筋混凝土支撑。基坑采用1 000 mm厚的地下连续墙作为围护结构,同时采用三轴混凝土搅拌桩对地下连续墙槽壁进行加固。地下连续墙深度为60 m,墙侧的土层共分9层,土层参数如表1所示。基坑采用顺作法施工,支撑形式为两道环形支撑加连杆和斜撑,内环圆形支撑直径为114 m,截面为2.2 m×0.9 m(宽×高);外环圆形支撑直径为128 m,截面为1.5 m×0.8 m;内外环圆形支撑之间的连杆截面为0.8 m×0.8 m;其他支撑杆件的截面为1.1 m×0.8 m;立柱桩截面为0.55 m×0.55 m,表2为支撑结构的截面信息。

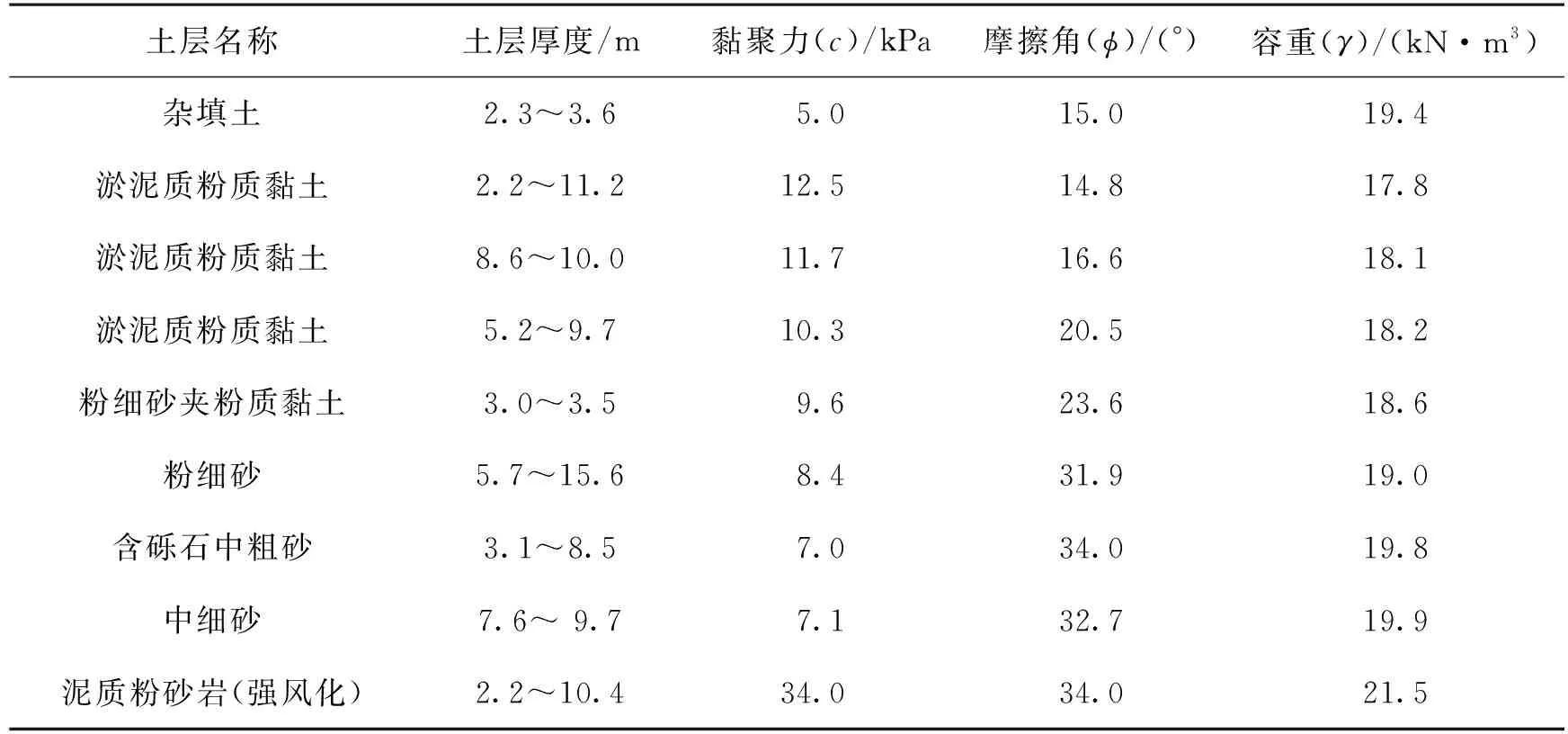
表1 基坑土层参数Table 1 Parameters of foundation pit soil

表2 支撑结构截面(宽×高)Table 2 Support structure section (width×height) m

采用ANSYS软件对基坑建模并进行模态分析,对基坑的混凝土支撑和立柱桩采用beam189单元模拟,地下连续墙采用shell181单元模拟;混凝土材料参数为重度2 400 kg/m3、弹性模量30 000 MPa、泊松比0.2,立柱桩钢材的材料参数为重度7 800 kg/m3、弹性模量345 000 MPa、泊松比0.3。模型如图2所示,材料参数如表3所示。

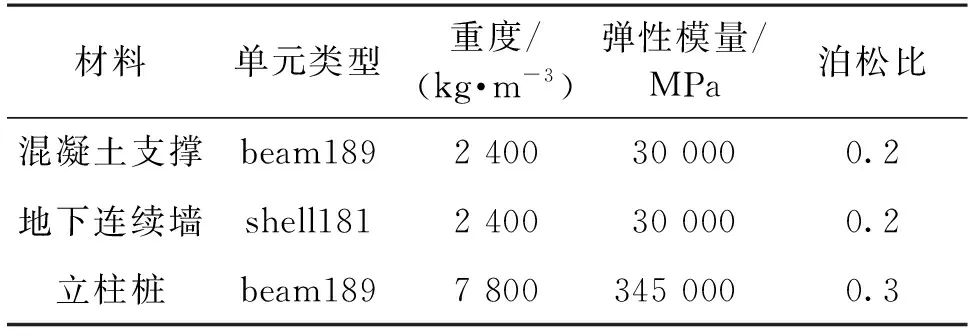
表3 材料参数Table 3 Material parameters

图2 基坑有限元模型Fig.2 Finite element model of foundation pit

模型建立完成后,对模型进行模态分析,结合基坑实际的变形特性,在基坑4个角的地连墙中点处施加x、y、z方向的自由度约束,选用Block Lanczos法提取模型的模态振型。对于大型的工程结构,结构的低阶模态即可反映工程的实际变形状况,计算基坑的前10阶振型,图3为模型的1～6阶振型。

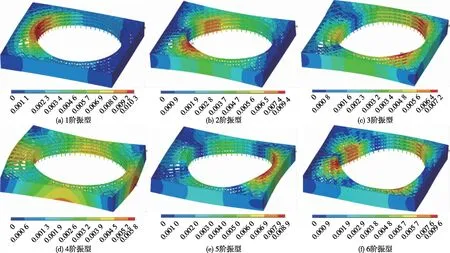
图3 模型的多阶振型Fig.3 Multi-order modes of the model

5.2 节点振型数据的获取与预处理

对于本次监测点的布置优化,选择165根基坑立柱桩顶部所在的位置为控制点位,从中选择20个点作为基坑的最优监测点。立柱桩所在的点位往往是基坑混凝土支撑的相交点,选择这些点位不仅可以监测混凝土支撑端部的水平和竖向位移,还能监测立柱桩顶部的水平和竖向位移。因此,本次布置的监测点能很好地监测基坑的安全状况,为基坑的安全施工提供科学的保障。

对所选取的控制节点进行重新编号[30],节点编号为1～165,每个节点都有x、y、z3个方向上的自由度,分别表示为(x1,y1,z1),(x2,y2,z2),…,(x165,y165,z165)(x、y、z分别为基坑结构横向、纵向和竖直变形方向),测点自由度编号为1～495。

5.3 基于粒子群算法的监测点优化

5.3.1 粒子群算法参数设置

粒子群算法的参数包括:种群规模、粒子范围、粒子最大速度、加速常数、惯性权重和最大迭代次数。

1)种群规模:即粒子群优化算法中的粒子数,一般取值为20～50。随着粒子数量的增多,相应的搜索密度增大,更有利于最优值的搜索,但算法运行的时间也会越长。

2)粒子范围:粒子范围通常与优化问题参数的取值范围相重合。对于多维的粒子群算法,粒子每一维也可以设置不同的范围。

3)粒子最大速度:粒子最大速度决定了粒子在一次迭代过程中可以移动的最大值。如果该值太大,粒子有可能会直接越过最优值;如果该值过小,会导致粒子因寻优能力不足而陷入局部最优值。

4)加速常数:加速常数一般用c1和c2表示,它是粒子朝着最优粒子的方向飞行的最大步长。c1和c2取值范围为[0,4]。

5)惯性权重:惯性权重用于保持粒子在运动中的惯性,使其有扩展搜索空间的趋势,取值范围通常为[0.2,1.2]。

6)最大迭代次数:寻优算法是通过不停迭代计算来寻找最优解,迭代次数越多,相应的计算时间就越长,当算法收敛后无需再进行迭代计算。最大迭代次数取值范围一般为[200,500]。

经过反复的计算和调参,得到较优的参数设置如表4所示。

表4 粒子群算法参数取值Table 4 Parameter values of the particle swarm algorithm

5.3.2 粒子群算法的优化计算

采用Python语言实现粒子群算法,选取基坑结构的10阶目标模态布置20个监测点。由于粒子群算法是随机类优化算法,所以程序每运行一次就会得到不同的优化结果,提取3次优化计算的结果进行分析,图4为适应度函数随迭代次数的变化曲线。

图4 适应度函数迭代收敛曲线Fig.4 Iterative convergence curves of fitness function

由图4(a)可以看出:第1次优化计算时,粒子群算法在迭代到接近175次时收敛,此时适应度函数最大值为0.783,对应的自由度序号为98、111、136、143、161、191、246、262、269、277、284、299、310、327、357、365、389、400、407、415。由图4(b)可以看出:第2次优化计算时,粒子群算法在迭代到160次左右收敛,此时适应度函数最大值为0.805,对应的自由度序号为46、128、140、143、147、159、171、189、219、241、248、262、272、275、306、313、344、346、360、423。由图4(c)可以看出:第3次优化计算时,粒子群优化算法在迭代到接近80次时开始收敛,此时适应度函数最大值为0.849,对应的自由度序号为147、151、165、170、190、218、222、242、249、254、258、268、282、292、296、303、311、345、374、384。

5.4 与传统监测点布置方案对比

图5为传统监测点和3次优化后的监测点布置方案对比结果。由图5可以看出:传统监测点的布置以均布和对称方式为主,监测点的选择主观性和经验性比较强,对于支撑形式复杂、跨度较大的基坑而言,监测点的布置缺乏科学性,基坑的安全性得不到有效保障;经过监测点优化后,3次优化后的监测点布置位置主要集中在支撑结构的内部环形支撑处,对比模型的模态振型图可以发现,测点布置的位置均集中在模态振型较大的位置处,与有限元模态分析的结果保持一致。优化后的监测点布置方案的监测有效性更高,监测方案更加科学,保障了实际基坑的安全。

图5 监测点优化对比Fig.5 Optimized comparison of monitoring points

6 结论

1) 基坑工程的监测内容较多,提出的监测点布置优化方法聚焦于基坑支撑结构,主要关注的是基坑支撑节点的水平和竖向位移,能够比较直观地把握基坑支撑的变形状况。

2) 通过分析基坑结构的力学特性,从基坑自身结构上寻找最优监测点布置方案,能让监测点在布置初期占据最佳位置。在基坑实际监测点布置中,根据监测信息的反馈,更加灵活地调整监测点布置,达到动态设计与信息化施工的目的。

3) 监测点优化借助基于MAC法的优化准则,使监测点的布置更加科学、有效,适用于紧邻城市道路、周边环境和支撑形式复杂的大型基坑,对于指导基坑工程的安全施工具有重要的意义。