路面交通诱发的振动对邻近地下遗址的影响

孟 江,朱利明,陈彦铭,张 森,黄 诚,杨书一

(1.南京工业大学 交通运输工程学院,江苏 南京 211800;2.南京工大桥隧与轨道交通研究院有限公司,江苏 南京 210032;3.无锡地铁运营有限公司,江苏 无锡 214000)

随着城市化进程的快速发展,交通基础设施不断完善,交通流量与日增加,交通拥堵问题仍未能得到有效解决,路面交通引发的邻近文物振动问题日益突出。如何科学合理地判定振动对文物的影响程度,确定道路与文物间的安全距离,是非常有必要的。目前,有关振动的影响研究主要集中在地上建筑[1-5],而路面交通诱发的振动对地下遗址的影响,相关研究大多集中在振动衰减规律、减隔振措施、影响因素等方面。

交通振动对文物的影响会产生累积效应,现已逐渐重视起来,相关人员开始研究各种防振隔振措施[6-9]。石玉成等[10]以甘肃山丹县新河驿明长城遗址为例,对各类车辆所产生的振动情况进行了分析,较为全面地反映了车辆荷载、车速、场地条件等因素对振动效应的影响,提出了不同类型遗址的振动安全限值。李思璐[11]以古椰贝丘遗址为背景,研究了高速公路诱发环境振动在土层中的传播与衰减规律,分析了隔振沟在不同参数下的隔振效果,给出了高速公路诱发环境振动的隔振沟模型参数。葛家琪等[12]以虎门炮台旧址为工程背景,通过实测及计算分析获得了古建文物振动响应随荷载、车速、多车效应及隔振沟尺寸变化的规律,以性能化指标对文物安全性作了评价。常鹏等[13]以虎门镇兵营遗址为研究对象,采用有限元进行动力时程分析,计算了兵营在不同荷载、车速下的振动响应,并分析了各因素对遗址的影响。目前,对文物的保护技术仍处于探索阶段,对地下文物评估方法及振动预测缺乏系统研究。

路面交通振动会对邻近地下遗址造成不利影响,文中以城上村遗址为背景,基于原位测试开展路面交通对城上村遗址的振动影响研究,研究成果以期为预测地下文物的振动响应提供试验基础和经验公式,为地下文物的防振保护提供科学依据。

1 文物概况及振动控制标准

1.1 文物概况

城上村遗址位于江苏省句容市,是新石器时代至周代时期的古遗址,现场文化堆积丰厚,有古代筑城的夯土层和环壕设施,是一处重要的吴国城址。

遗址南北长,东西短,略呈长方形,北部地势较高,与周围地表高差达7～8 m,南部较矮,是目前苏南地区同类遗址中保存最好的一处,被国务院核定为第七批全国重点文物保护单位。遗址东侧为304县道,距离遗址保护线最近约70 m,遗址现场文化堆积丰厚,其现状平面如图1所示。

图1 城上村遗址平面图Fig.1 Plane figure of Chengshang Village ruins

城上村遗址面积大,保存状态较好,文化堆积层厚度约4 m,面积约97 625 m2,遗址现场出土较多陶片,借鉴考古队的勘探资料[14],其地层堆积如图2和表1所示。

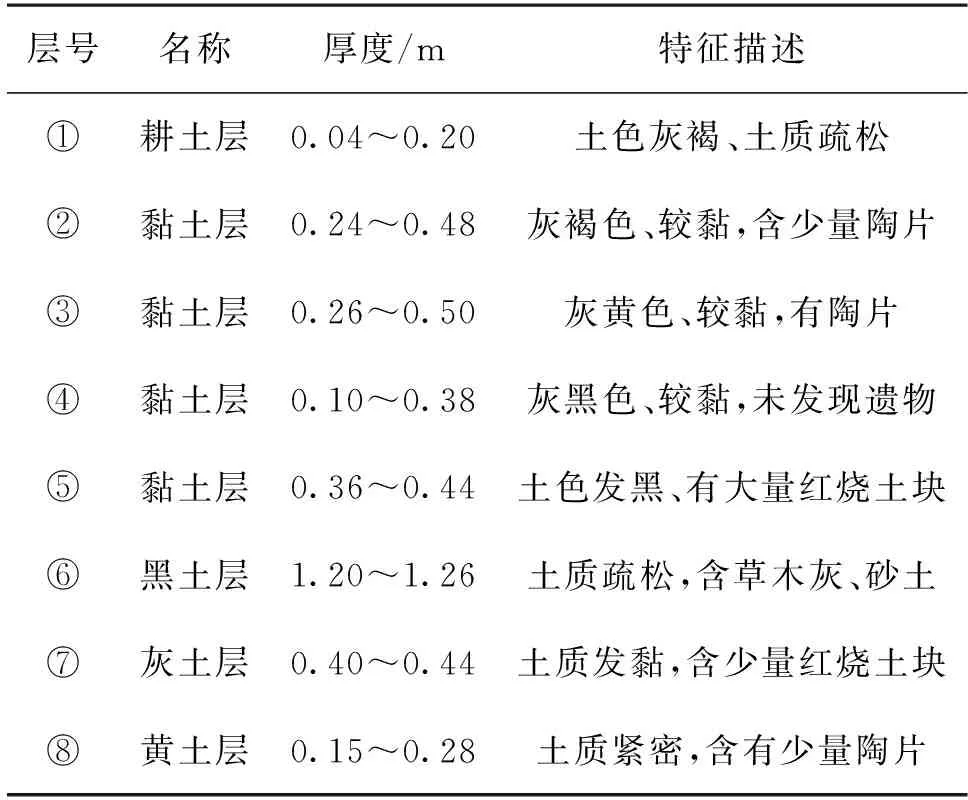
表1 地层堆积情况描述Table 1 Description of stratum accumulation

1.2 振动控制标准

城上村遗址的材质主要为土,对于地下遗址的振动速度限值暂无相关规范。由于土质结构弹性波速一般为90～500 m/s,参考《古建筑防工业振动技术规范》(GB/T 50452—2008)[15]及文献[10]研究成果,城上村遗址水平振动速度限值取0.15 mm/s。

2 冲击振动现场试验

2.1 测试仪器

振动测试系统包括拾振器、数据采集仪、计算机等。数据采集仪采用北京东方振动和噪声技术研究所的INV9580A型无线振动采集仪,该采集仪内置水平和垂直双通道高精度拾振器,可实现双核24位高精度采集,最高采样频率为256 Hz,频率示值和分辨率误差小于0.01%,测振器的灵敏度为24 V·s/m,量程为0.1 m/s。

2.2 测试方法

沿行车道和城上村遗址之间布设测点,对地表及遗址进行振动测试。在整个测试过程中分别考虑不同车速和不同测点位置所产生的振动响应,为反映车辆在不同时段内引起的振动效应,采集系统对测试全过程进行实时跟踪和记录。

2.3 测点布置

为研究地面及遗址的振动响应及衰减规律,结合试验场地的具体条件,在城上村遗址和行车道之间选择7个位置,在地表布置振动监测点,每个测点分别布设1个振动探测仪,其X方向垂直于行车道方向。监测点距行车道的距离分别为2.5、5.0、10.0、20.0、35.0、50.0和70.0 m,监测点平面位置如图3所示。

图3 振动测点布置平面示意图(m)Fig.3 Layout diagram of vibration measuring points (m)

2.4 测试工况

现场实测选择在深夜进行,以避免行车干扰,考虑到不利情况,现场采用30 t重型卡车,分别以10、20、40和60 km/h的车速驶过,每个工况进行3次数据采集,采集时长约10 min,以记录测试全过程。加载处布置5 cm高的减速带以模拟冲击效应。

3 结果与分析

3.1 测点振动速度响应

为探究城上村遗址因行车引起的环境振动特点及传播规律,测试不同工况下各测点的振速峰值,结果见表2。

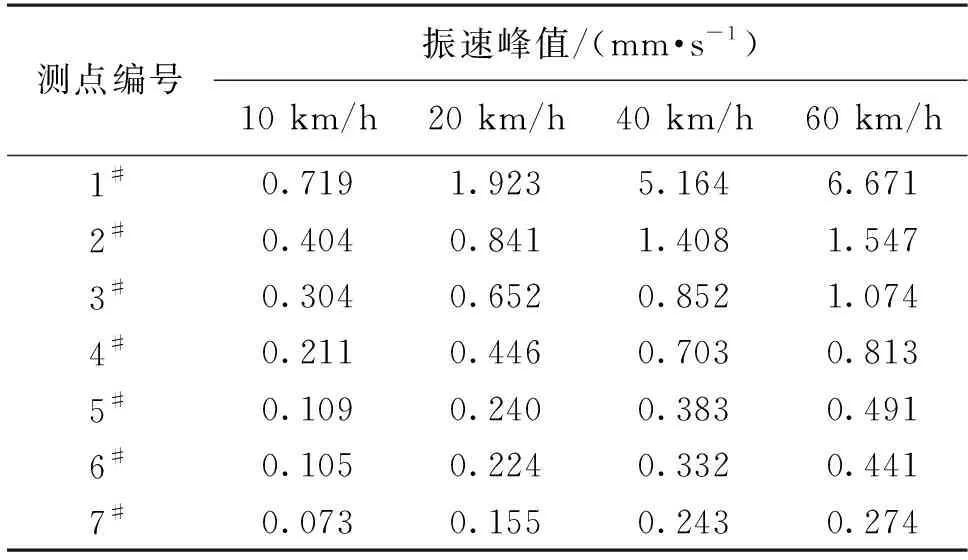
表2 振速峰值测试结果Table 2 Test results of peak vibration velocity

由表2可知:振速峰值响应与车速正相关,车速由10 km/h增至60 km/h,距振源10 m处振速峰值响应增加253.3%;振速峰值响应与振源距离呈反相关关系,以车速10 km/h为例,振源距离由2.5 m增至70.0 m时,振速峰值响应减少89.8%。

基于表2测试结果,不同测点位置、车速所产生的振动速度均存在较大差异,由于汽车荷载较大,加之减速带“冲击效应”影响,振动速度对车速的变化较为敏感。另一方面,汽车振动产生的能量密度在传播过程中存在衰减现象。

图4为不同车速下各测点振速峰值的变化曲线。

图4 不同车速下振速峰值响应Fig.4 The peak vibration response of different travel speeds

由图4可知:路面交通荷载引发的振动速度随振源距离的增加而逐渐衰减,近距离振动速度衰减极快,35 m外振动速度趋于平缓;车速的影响主要体现在近距离振动,对于远距离振动,车速影响较小。

不同测点位置在各车速下的水平振动响应时程曲线如图5所示。

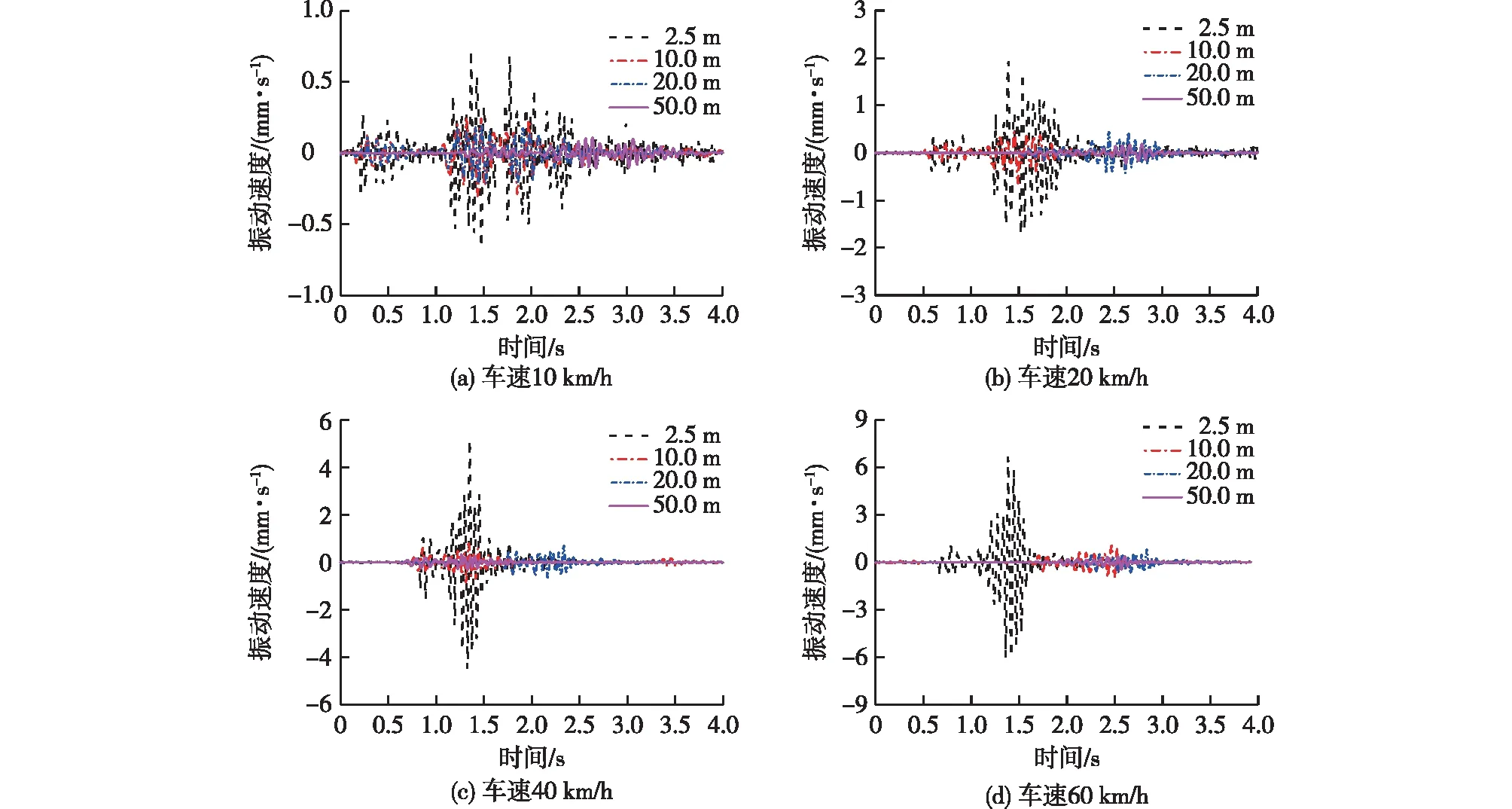
图5 不同测点位置振动响应时程曲线Fig.5 Time-history curves of vibration response at different measuring points

由图5可知:对于相同的车速,水平振动速度响应随着振源距离的增加而减小;此外,对于远距离振动,由于振动传播的时效性,有着明显的“振动滞后”现象。

3.2 振动速度频谱分析

不同测点位置在各车速下的水平振动速度频谱如图6所示。

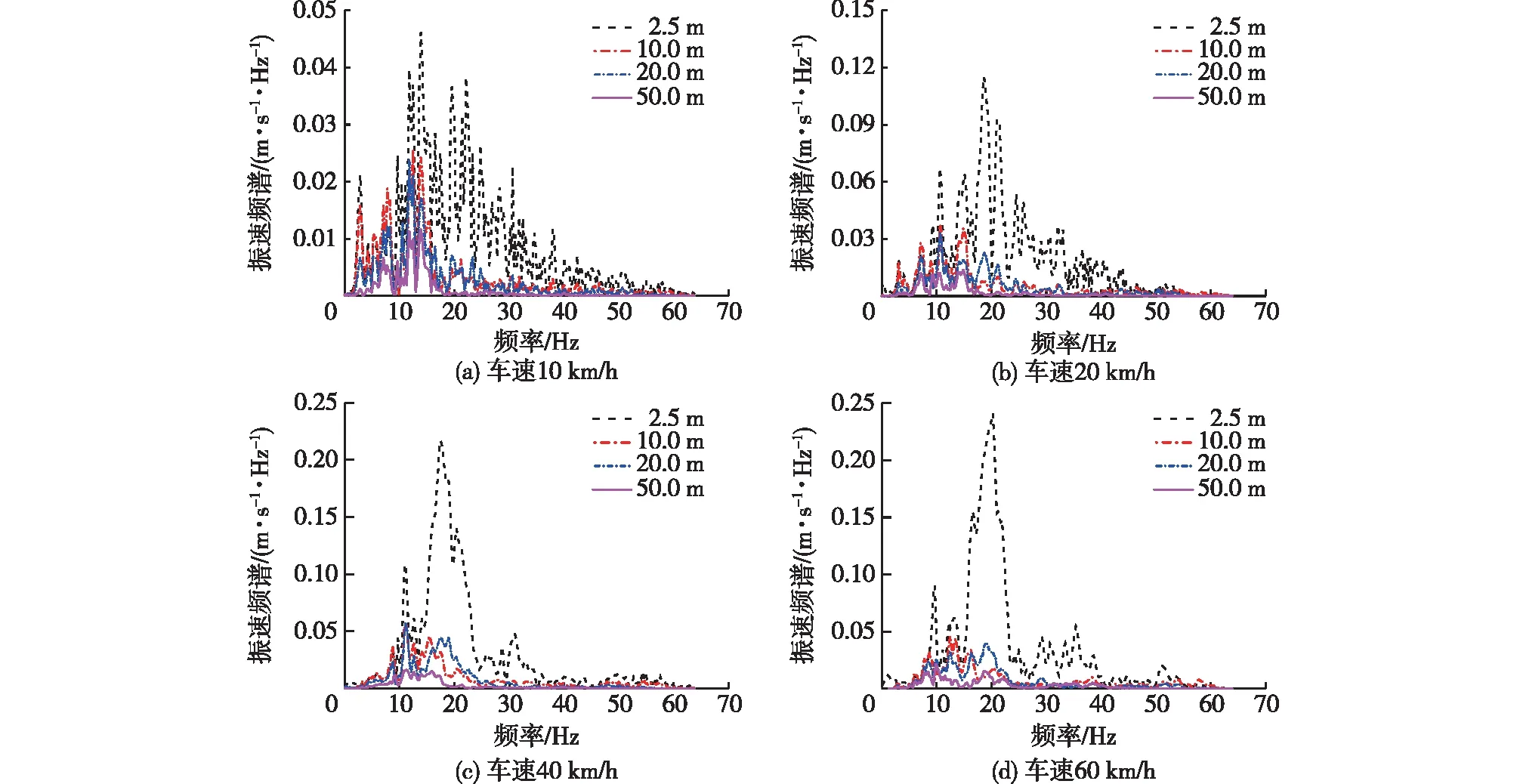
图6 不同车速下振动速度频谱响应Fig.6 Vibration velocity spectrum response at different travel speeds

从图6可以看出:振动速度频谱的卓越频段分布为0～40 Hz,当车速较低时,在10和20 Hz附近有两个主频,随着车速的提高,20 Hz附近的振动频带逐渐显著;对于远离振源的位置,各频率的振动速度基本上随距离的增加而减少,其中高频振动的衰减速度明显高于低频振动,监测点的水平振动速度以低于20 Hz的低频振动为主。

4 振动衰减规律及安全距离计算

根据现有的研究理论[16-19],振动衰减受波前几何扩散和介质吸收的双重影响。由于实际工程中,地层并非理想的线弹性介质,振动传递过程中,地层吸收了部分振动能量,造成振动能量以指数形式衰减;另一方面,振源激励与车速有关,在水平方向上沿四周扩散,随着传播距离的增大,其能量密度按幂函数规律衰减。

参考现有的理论基础,对实测数据进行统计分析,振动速度与振源距离的衰减规律可表示为式(1)。

(1)

式中:v为振动速度;k为当量系数,其数值与冲击能量和场地介质条件有关[20-22];v0为车速;a为与车速有关的指数;r为测点至振源的距离;b为几何阻尼衰减系数;c为土的能量吸收系数,与土的工程性质有关。

为验证式(1)的适用性和准确性,对城上村遗址不同车速下实测数据进行拟合分析,不同车速下振动速度随振源距离的衰减关系曲线如图7所示。

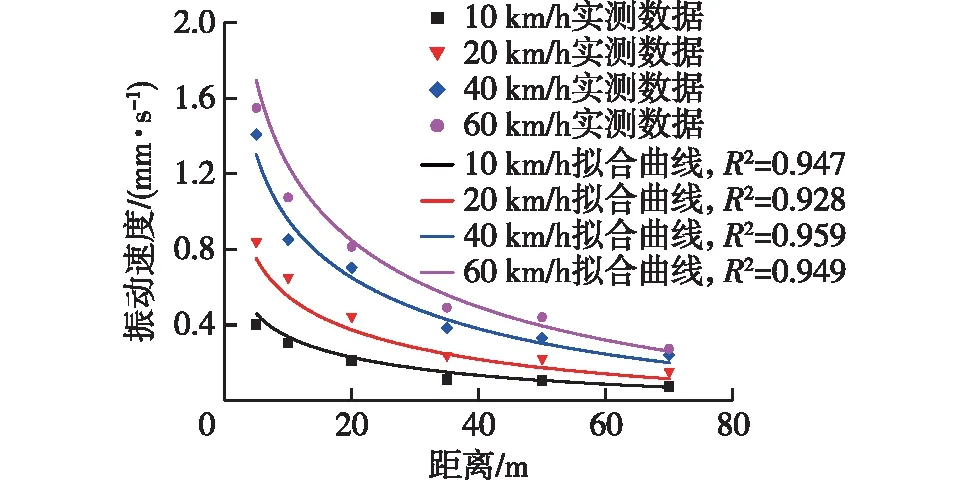
图7 振动速度随距离的衰减关系曲线Fig.7 Decay relationships between vibration velocity and distance

由图7拟合结果可知:振动速度衰减拟合曲线与现场实测数据吻合性较好,表明式(1)能够较好地描述行车荷载振动的传播规律,具体函数关系可表示为式(2)。

(2)

由图7和式(2)可得:不同车速下振动响应随振源距离的变化规律相似,振动速度与振源距离呈指数函数衰减,与车速呈幂函数递增。参考《古建筑防工业振动技术规范》(GB/T 50452—2008)及相关文献研究成果,取振动速度临界值为0.15 mm/s,对于给定的车速,可以通过式(2)反算安全距离。由式(2)可知,对于给定的振动速度限值,随着车速的提高,安全距离也随之增大,二者呈正相关关系,由二者拟合曲线可绘制文物振动安全区域,如图8所示。

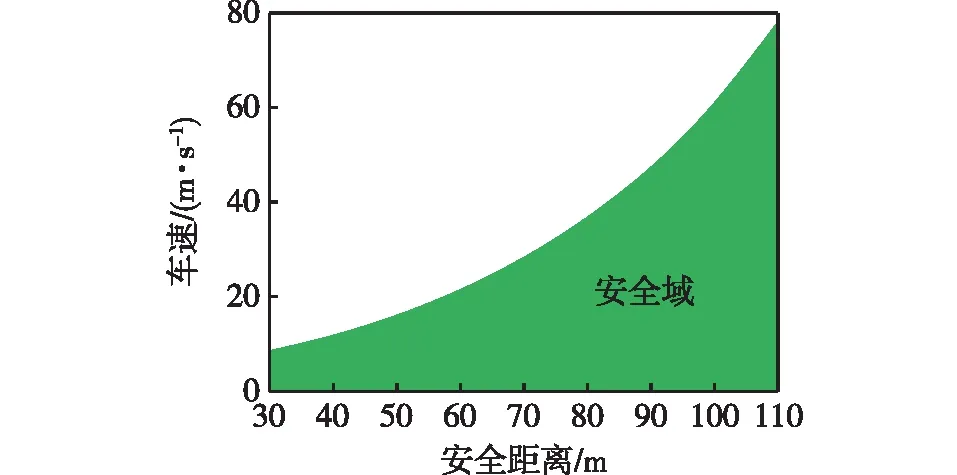
图8 车速确定的振动安全区域Fig.8 Vibration safe area determined by travel speed

5 结论

通过对30 t重型卡车经过减速带时的振动进行现场试验研究,分析了不同车速在各测点位置诱发的振动响应及传播规律,得到以下结论:

1)不同车速下振动响应随振源距离的变化规律相似,随着振源距离的增加,振动速度呈指数函数衰减;振动速度随着车速的增加而增大,总体呈幂函数关系。

2)通过减速带引起的振动响应卓越频段为0～40 Hz,各频段振动速度随着振源距离的增加而减少,其中高频振动的衰减速度明显高于低频振动。

3)结合现场试验数据,建立了振动速度与车速和振源距离的一般函数关系,得到了车速对邻近地下文物振动影响的经验参数,研究可以预测文物振动,对于文物保护具有一定的借鉴意义。

4)在确定的荷载和振动速度限值条件下,安全距离随着车速的提高而增大,因此,确定文物安全距离时,需要考虑邻近路段限速要求。