基于改进果蝇算法优化的最小二乘支持向量机动力锂电池荷电状态预测
李雪林,孙玉坤
(1. 江苏旅游职业学院 信息工程学院,江苏 扬州 225001;2. 江苏大学 电气信息工程学院,江苏 镇江 212013)
目前电池荷电状态(SOC)主要的预测方法(内阻特性法、等效电路法、安时计量法、内阻特性法、估计开路电压法、卡尔曼滤波器递推算法、神经网络法等)基本是对电池工作中发生的物理及化学变化进行分析,并在数学方程基础上建立的预测模型[1-7],这些模型的缺点是前置了许多条件和先验参数,导致求解过程繁琐且模型预测精度不能满足工业要求。最小二乘支持向量机(LSSVM)将标准支持向量机(SVM)的学习问题转化为线性矩阵求解问题,明显提高求解速度,有效解决了SVM算法的缺陷,并且LSSVM具有结构风险最小化的优点[8-13],其利用样本数据在训练过程中确定结构参数,从而不会出现过拟合问题,但LSSVM模型的参数选取不当可能会严重影响预测结果的精确性[14-21]。本文分别运用果蝇算法和改进果蝇算法对LSSVM参数进行优化,用改进果蝇算法优化的LSSVM设计动力锂电池 SOC 混合预测模型。
1 最小二乘支持向量机
LSSVM是在SVM基础上进行改进的, 通过引入损失函数、误差平方、等式化约束的方法,避免了求解二次规划问题,将求解最优化问题变为求解线性矩阵问题,使得算法的复杂度降低,和SVM相比,LSSVM的运算速度较快。
基于LSSVM的回归预测:对于非线性样本集s={(xi,yi)|i=1,2,…,n},其中n为样本数量,xi∈Rn,为样本输入向量;yi为样本输出。
通过非线性函数p(x)映射到高维特征空间,再进行线性回归,即
f(x)=wTp(x)+b
(1)
式中:w为n维权重向量,b为偏差,f(x)为线性回归表达式。
通过风险最小化原则,可以转化为等式约束下的优化,如式(2)所示。
s.t.γi[wTp(x)+b]=1-φi,i=1,2,…,n
(2)
式中:γ为惩罚函数,φ为松弛变量,J(w,φ)为最小二乘支持向量机的损失函数。
引入Lagrange系数(αi),将式(2)构造成无约束目标函数(Q),如式(3)所示。
Q(w,b,α,φ)=J(w,φ)-
(3)
式中:αi为拉格朗日乘子。
对式(3)中的w,b,α,φ求偏导,并令其偏导数为0,则利用对偶关系的线性Karush-Kuhn-Tucher(KKT)条件,消除w、φ后,最优可得
(4)
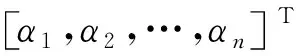
由α、b可得LSSVM回归模型,如式(5)所示。
(5)
式中:K(x,xi)为满足 Mercer 条件的任何对称的核函数对应于特征空间的点积。
在没有先验信息条件下,一般求解非线性问题时,采用径向基核函数设计的模型,其具有测试误差小、数据更精确的优势。本文在构造LSSVM 回归模型时采用径向基核函数,如式(6)所示。
(6)
式中:σ2为核函数的宽度。
2 果蝇算法(FOA)原理
果蝇算法是在观察果蝇寻找食物中发生的一系列行为中总结提出的具有智能寻优特点的算法。果蝇有着无与伦比的嗅觉,在获取食物的气味后会向气味方向搜索,然后在视觉作用引导下找到果蝇伙伴和食物的目标位置,然后再朝目标飞去。研究表明:果蝇搜索食物的气味浓度与食物的距离成正比关系。果蝇通过不间断地搜索,逐渐会从气味浓度小的地方慢慢逼近气味浓度大的地方,如此反复,最终在搜索到食物后结束。
分析果蝇搜寻食物过程,总结出果蝇优化算法的展开顺序。
1)采用随机方法对果蝇群体位置的横、纵坐标进行初始化设定,分别为xinitial和yinitial。
2)给出果蝇个体在嗅觉作用引导下搜寻食物的随机方向和距离(drandom),如式(7)所示。
(7)
式中:xi和yi分别为果蝇位置的横、纵坐标。
3)测算果蝇与坐标原点的距离(Di),然后计算食物气味浓度判定值(Ji),分别如式(8)和(9)所示。
(8)
Ji=1/Di
(9)
4)在食物气味浓度判定函数(F)的基础上,代入食物气味浓度判定值(Ji),可以获得该果蝇个体位置获得的气味浓度(S(i)),如式(10)所示。
S(i)=F(Ji)
(10)
5)将获得气味浓度最大的果蝇从所有果蝇群体中识别出来,如式(11)所示。
[bS,bI]=max (S(i))
(11)
式中:bS为当前气味浓度最大值,bI为获得当前气味浓度最大的果蝇序号。
6)标注气味浓度最大值(Smax)和位置坐标,则果蝇群体在视觉作用下朝该坐标飞去,如式(12)和(13)所示。
Smax=bS
(12)
(13)
7)进行迭代寻优,重复1)—6)步骤,并判断气味浓度是否大于前一迭代气味浓度,若是,则继续执行步骤6)。
3 改进果蝇算法(IFOA)原理
在果蝇算法(FOA)中,气味浓度判定式为Ji=1/Di,是距离的倒数。而距离Di的数值范围相当大,所以Ji非常容易早熟,只在非常小的空间进行搜索,搜索没有覆盖所有范围,得到的仅仅是局部范围内的最优解,并非全局最优解。针对这个缺陷,对果蝇算法(FOA)进行改进,将气味浓度判定式进行了改进。
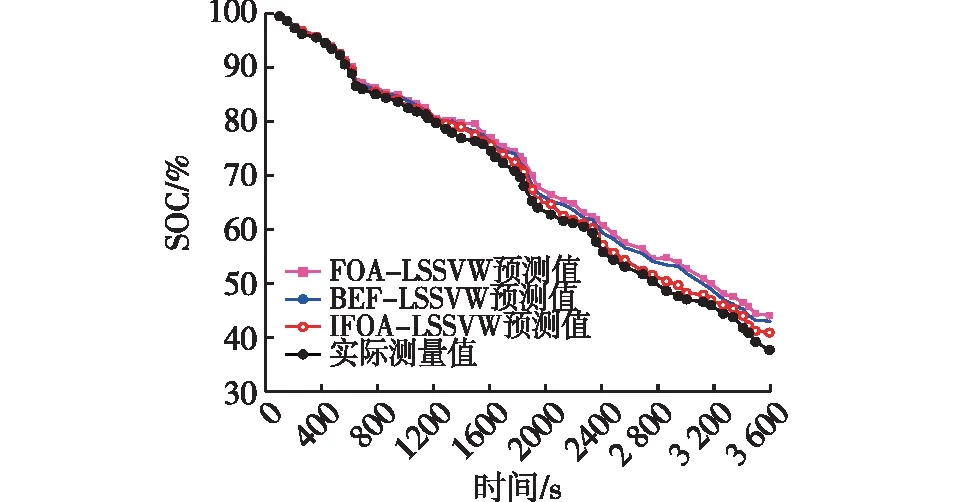
1)对最大迭代次数(M)进行初始化,设定毎次迭代循环时的气味浓度判定值为Ji(l)(1 2)设定“悬停”状态和“悬停时间”。 如果某个果蝇某次迭代的搜索状态满足下列条件 S(l)=S(l-1) (14) S(l)<0.99 (15) 式中:S(l)为某个果蝇某次迭代时搜索到的最大气味值。 则此时就被标记为“悬停”。 “悬停时间”设为t(t=1,2,…),t S(l)=S(l-t) (16) S(l)≠S(l-t-1) (17) 3)修改气味浓度判定值Ji(l),修改后的表达式为 Ji(l)=1/Di(l)+k(l)×Di(l) (18) (19) 在式(18)中增加一个松弛项k(l)×Di(l),k(l)能够自适应变化,加大了气味浓度判定值Ji(l)的分布范围,避免在寻优过程中陷入局部最优解。 在训练样本集和径向基函数(RBF)核函数确定之后,LSSVM模型同样对惩罚因子(γ)和核函数参数(σ2)进行设定。γ是用来对 LSSVM的置信范围和经验风险的比例进行调控的,γ泛化能力在取中间值时效果最佳。σ2的主要作用是描述训练样本数据的分布特性,对局部领域的范围进行设定,σ2的数值和方差成反比关系。由此可见,LSSVM的学习能力和泛化能力受γ和σ2的影响非常大。寻找参数γ和σ2最优值能够很好地改善LSSVM 的性能。笔者利用改进果蝇算法(IFOA)对LSSVM中的γ和σ2进行优化,其表达式为 γi(l)=C1Ji(l)(1,1) (20) (21) 式中:C1和C2为常量,Ji(l)为1×2维的矢量。 气味浓度的判定值Ji(l)是由LSSVM中的相关系数(R2)和均方根误差(E)的差值决定的,如式(22)所示。 Ji(l)=R2-E (22) 1)对动力锂电池SOC预测模型的输入函数和输出函数进行确定; 2)归一化处理输出样本数据,用于建立LSSVM样本集,利用训练样本寻找LSSVM 的最优参数集; 3)确定LSSVM 中参数γ和σ2的初值; 4)参数γ和σ2初值确定后,利用训练样本集对 LSSVM进行训练,建立动力锂电池SOC的预测模型; 5)基于IFOA对参数γ和σ2进行寻优; 6)利用得到的γ和σ2继续对LSSVM预测模型重新进行训练,多次返回步骤4),确认得到最优预测模型后终止; 7)用得到的最优预测模型对动力锂电池进行SOC预测,根据预测结果对比实测结果,进行针对性的误差分析。 要对电池SOC进行精准预测,首先要选择合适的输入和输出参数。电池的输入和输出参数主要有电流、电压、内阻和温度等。对动力锂电池工作状况进行研究后发现:影响电池SOC最关键的参数是电池的工作电压(U)和工作电流(I),所以提取工作电压和工作电流这2个核心参数对动力锂电池进行SOC预测。 本仿真实验选取的动力锂电池是磷酸锂电池,型号为DEC100, 其铭牌额定电压 3.3 V, 铭牌额定容量为1.1 A·h。采用可编程电源对电池进行充电,电子负载对电池进行放电,以保证电池充放电的有序进行及数据的完整性,利用电脑记录检测到的电压和电流数据信号。为了避免电池过充、过放,采用电子智能数字测量仪对动力锂电池端电压进行实时跟踪监测。 分别在 0.5、1.0、2.0、3.0放电倍率下重复进行恒流放电测试,获取电池数据。通过式(22)进行数据归一化处理后得 (23) 采集到64组电压和电流数据,选取其中一部分数据作为训练集,另一部分数据作为测试集(表1)。 表1 部分测试集数据Table 1 Partial test set data 为了检验模型的预测效果,根据IFOA算法的寻优过程,本文设置种群规模为30、迭代次数为100、步长为10,将由LSSVM中的相关系数(R2)和均方根误差(E)的差值来作为浓度判定函数,将表1中的测试样本输入基于IFOA优化的LSSVM预测模型,仿真结果见图2。由图2可知:LSSVM预测模型对电池SOC预测结果和实测结果吻合度很好,其平均绝对误差(MAPE)为1.02%,充分说明预测结果具有较高的精确性。 图2 实际测量与仿真SOC曲线Fig.2 Actual measurement and simulated SOC curve 为了对预测模型的泛化能力做出客观评价,并检验其实用性,在MATLAB平台上模拟汽车行驶时加速、减速、怠速和匀速的各种情况,在该工况下对电池进行放电,采集样本数据。为了展现电池在该工况下的实用性,将仿真所用的锂电池利用电池盒拼装成一个电池组, 设定V=19.8 V,C=11 A·h,采集放电过程中的数据(表2)。 表2 参数优化和性能对比Table 2 Parameter optimization and performance comparison 将采集的电流和电压数据输入FOA-LSSVM算法、贝叶斯-LSSVM算法(BEF-LSSVM)和IFOA-LSSVM优化算法所建预测模型中,其输出结果如图3所示。 图3 输出结果曲线Fig.3 Output result curves 由图3可知:与FOA-LSSVM、BEF-LSSVM预测模型相比,IFOA-LSSVM优化算法所建预测模型的电池SOC预测结果与实际测量结果更接近,说明其泛化能力强,预测精度也远远超过另外2个预测模型。在参数优化、迭代次数、运行时间上,IFOA-LSSVM预测模型明显优于FOA-LSSVM和BEF-LSSVM预测模型,而且由于模拟实际工况下电池的电流波动幅度大, 更加能够证明IFOA-LSSVM预测模型进行 SOC预测时,具有更好的效果。基于IFOA优化的最小二乘支持向量机预测电池 SOC满足工业精度的要求,具有良好的预测效果,表明IFOA-LSSVM预测SOC方法可行。 1)在节能减排、能源替代的大背景下,动力电池SOC的预测一直是国内外电动汽车电池管理系统研究的热点。由于部分缺陷,果蝇算法在寻优时可能得到的是局部最优解而不是全局最优解,笔者在果蝇算法的基础上进行了改进,增加了一个自适应松弛项,从而加大了浓度判定值的分布范围,并用改进后的果蝇优化算法优化选取支持向量机的参数。 2)建立了基于IFOA优化的LSSVM预测SOC模型,并应用于锂电池的SOC预测, 仿真实验结果表明, 基于交叉训练的IFOA优化LSSVM的SOC 预测模型,对LSSVM进行参数寻优,能够极大提高参数的寻优效率,减少迭代次数,显著地提升LSSVM预测模型的精度,完全避开了分析电池复杂的物理化学过程与求解数学方程,IFOA优化的LSSVM预测SOC方法可行,并具有较高的准确性。4 LSSVM 的参数优化和预测模型实现
4.1 LSSVM 的参数优化
4.2 预测模型实现流程
5 实例测试数据的获取及处理
5.1 输入和输出参数的选用
5.2 测试对象和方法
5.3 测试数据的获取与处理
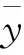
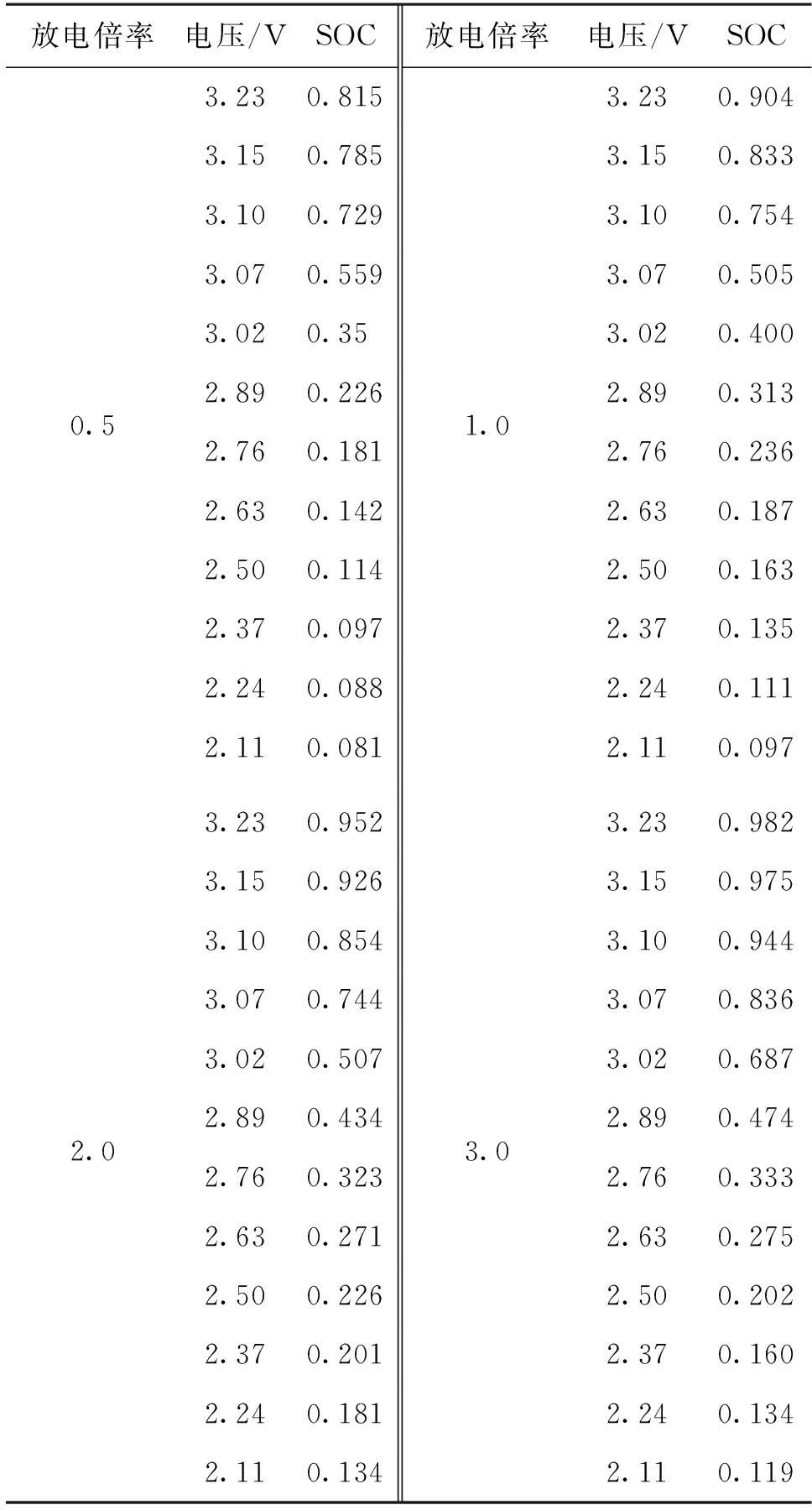
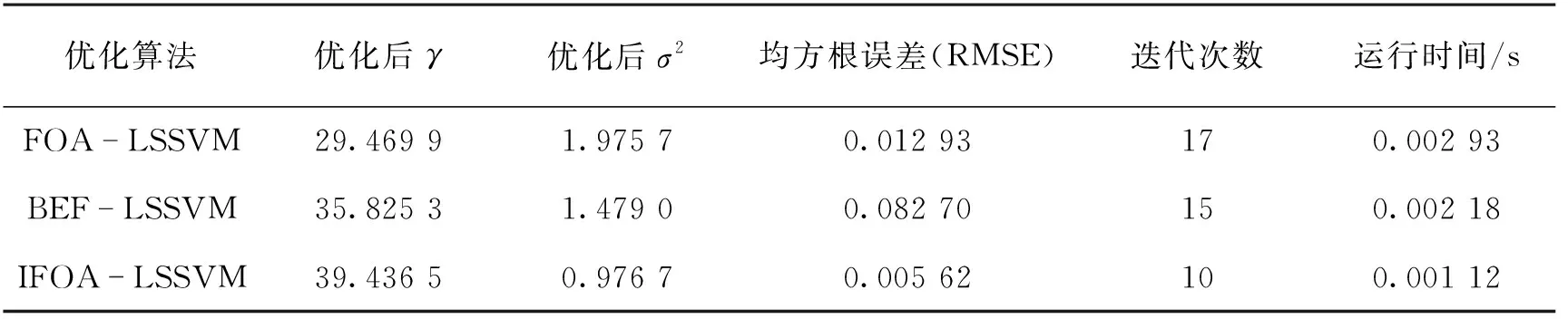
6 基于IFOA优化LSSVM动力锂电池的SOC预测分析
6.1 仿真结果与分析

6.2 模型评价
7 结论

