紧凑型热管真空管集热器集热特性分析

支黎明,杨谋存,朱跃钊,姜 琴,张志毅,王薪贺

(南京工业大学 机械与动力工程学院,江苏 南京 210009)

随着全球能源短缺和环境恶化的影响加剧,大力发展可再生能源成为迫切需求[1-2]。在当前能源使用总量中,建筑和工业耗能占比最大,其中建筑耗能中的30%为空调需求,工业过程中353.15～523.15 K的热能需求约占40%[3]。太阳能以其清洁、无污染的优点较其他能源更具优越性。另外,我国约有100亿m2闲置屋顶[4],如能把太阳能聚光器与建筑屋顶结合起来,既可以部分满足建筑和工业耗能中温热能需求,又能解决太阳能聚光器占地面积大、热能难以远距离输送等难题[5]。因此,研究可与建筑结合的太阳能聚光器对于节能减排和双碳目标的实现具有重要意义和工程价值。

为与建筑有效结合,冯晨等[6]设计了一种聚光比为3.4、厚度为120 mm的微型抛物槽集热器,其最大瞬时热效率为67.23%,工作温度小于473.15 K。为提高集热器热性能,Gu等[7]设计了一款真空型复合抛物线集热器,尽管其尺寸较小(90 mm × 72.6 mm × 80 mm),但热性能相比非真空型显著提高,驻点温度可达600.15 K。Sultana等[8]发现使用选择性吸收涂层的集热器比不使用的聚光器热性能提高10.00%。Muschaweck等[9]提出了一种在实际约束下非跟踪式太阳能集热器寻找最佳反射器形状的方法,优化后的集热器能在工作温度453.15 K下保持50.00%的热效率。李雪岭等[10]和宋子旭等[11]基于集热器的腔式结构,分别设计了“优弧型”和吸收体为矩形的腔式集热器,均在一定程度上提高了集热器热性能。此外,使用纳米流体能提高热性能,Alqaed等[12]发现使用CuO纳米流体的集热器热效率相对传统集热器性能更佳。

总体上,在太阳能集热器的研究中,对提高传统尺寸的集热器热性能的研究较多,而对集热器与建筑结合的研究相对较少;在对集热器影响因素分析时,仅仅考虑了单一因素对集热器热性能的影响,而多因素同时对集热器热性能的综合作用研究较少;另外,相关优化改进的集热器,结构上比较复杂,不利于生产制造。

笔者设计了一种紧凑型热管真空管太阳能集热器(HPETC),其体积小、质量轻、结构简单,可与建筑有效结合。建立了一维稳态传热模型,从传热热阻角度,讨论进口温度、真空管内压力、选择性吸收涂层(SAC)发射率和直射辐射对集热器集热性能的影响;使用方差分析法,研究4种因素的综合影响程度,为紧凑型太阳能集热器的性能提升提供一定的参考依据。

1 集热器结构

紧凑型热管真空管太阳能集热器结构主要分为3部分:跟踪单元、集热单元和管道及框架等支撑单元,具体组成结构如图1所示。由图1可知:集热器由6个并行排列的集热单元组成,每个单元由抛物槽、真空管和热管构成,且真空管和热管轴线、抛物槽焦线和转动轴线重合。真空管为全玻璃双层真空管,其内管外层的SAC为黑铬材料。热管为铜-水重力热管(工作温度≤523.15 K),每根热管的冷凝段均插入歧管,便于管内流体工质获得热量。步进电机组件和连杆机构等组成集热器动力单元,使得集热单元能够实时或间歇追踪太阳,可实现抛物槽反射镜对太阳的一维跟踪。所设计的集热器结构尺寸如表1所示,安装方式为南京地区(32° N)南北轴向倾斜32°。

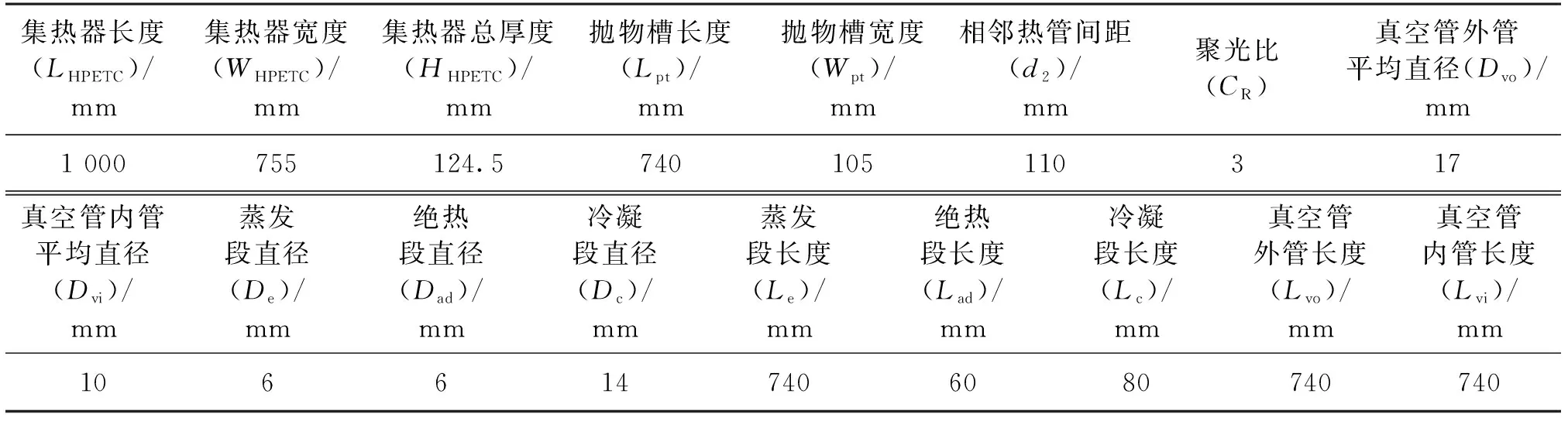
表1 集热器结构参数Table 1 Structural parameters of the collector

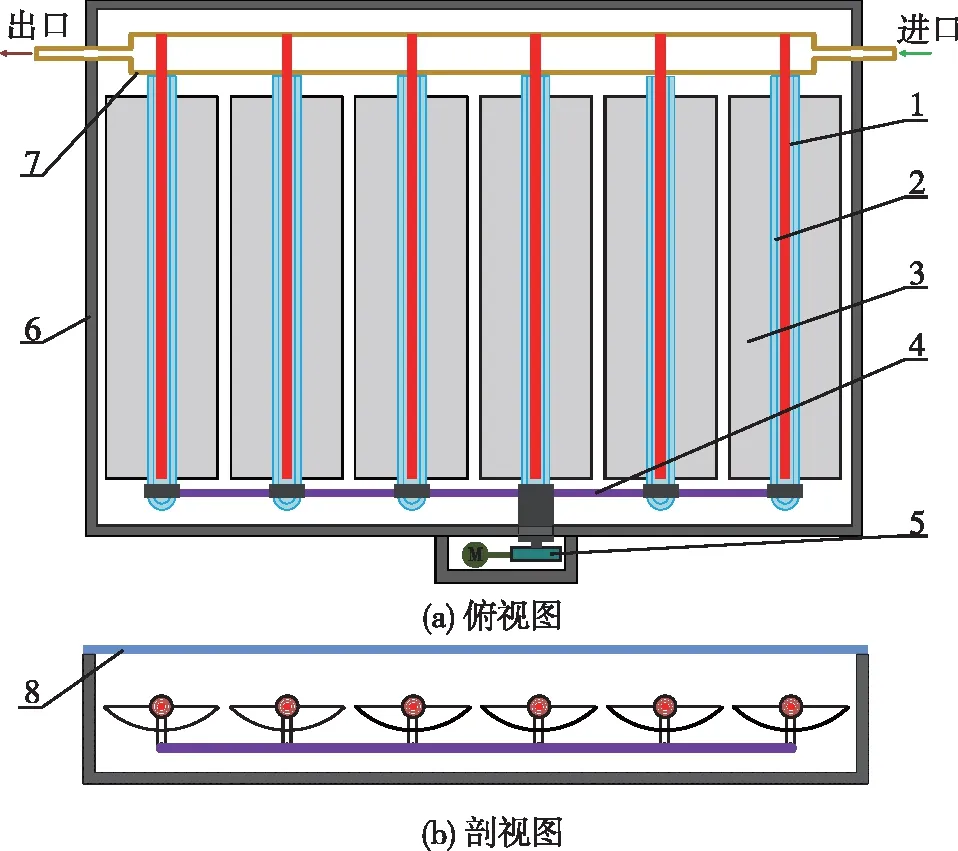
1—热管; 2—真空管; 3—抛物槽; 4—跟踪装置; 5—平面连杆机构; 6—框架; 7—歧管; 8—玻璃盖板图1 集热器结构示意图Fig.1 Schematic diagram of the collector

2 集热器稳态传热模型

2.1 传热过程分析

热性能是评价太阳能集热器性能的重要指标,为此需要对集热器进行热分析。经分析可知,太阳能透过玻璃盖板和真空管被SAC捕获,并在SAC中转化为热能。一部分能量从真空管内管,通过L-QB300导热油传递至热管蒸发段,经热管相变换热,能量迁移至冷凝段,流体工质以对流换热的形式吸收冷凝段释放的热量;另外一部分能量则以热辐射、热传导和对流换热的形式向外耗散。该集热系统的传热过程可通过传热热阻进行表示,集热器传热热阻模型如图2所示。

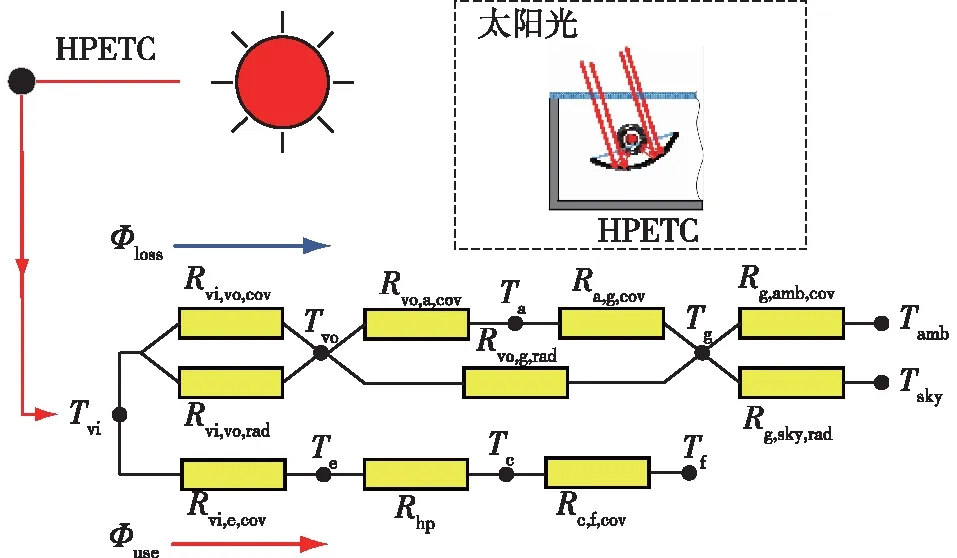
图2 集热器传热热阻模型Fig.2 Heat transfer resistance model of the collector

集热器热效率(ηth)计算式为

(1)

式中:Ag为玻璃盖板面积,m2;Ib为太阳直射辐射,W/m2;Qf为流体工质吸收的热量,J。

图2中:Rvi,vo,cov为真空管内管与外管间对流换热热阻;Rvo,a,cov为真空管外管与集热器内部空气间的对流换热热阻;Ra,g,cov为集热器内部空气与玻璃盖板间的对流换热热阻;Rg,amb,cov为玻璃盖板与环境间的对流换热热阻;Rvi,vo,rad为真空管内管与外管间辐射热阻;Rvo,g,rad为真空管外管与玻璃盖板间的辐射热阻;Rg,sky,rad为玻璃盖板与天空间的辐射热阻;Rvi,e,cov为真空管内管与热管蒸发段间的对流换热热阻;Rhp为热管冷凝段与蒸发段间的热阻;Rc,f,cov为热管冷凝段与传热流体间的对流换热热阻;Tvi为真空管内管温度;Tvo为真空管外管温度;Ta为集热器内部空气温度;Tg为玻璃盖板温度;Tamb为环境温度;Tsky为天空温度;Te为热管蒸发段温度;Tc为热管冷凝段温度;Tf为传热流体温度;Φloss为集热器损失的能量;Φuse为集热器获得的有用能量。

2.2 数学传热模型

根据热力学第一定律,可建立集热器各传热部件一维稳态传热模型。为了简化数学模型,做出如下假设:

1)基于等效热管的概念,将重力热管等效为热超导金属棒[13];

2)忽略玻璃盖板及真空管的热传导,并忽略真空管端部热损失,框架、歧管与周围隔热[14];

3)真空管、玻璃盖板和空气的物理性质稳定;

4)SAC吸收的太阳能量以内热源的形式分配给真空管内管;

5)集热器工作状态稳定。

因此,各传热组件热力学方程及相关传热系数计算如下文所示。

2.2.1 集热器获得的太阳能量

真空管内管获得的太阳能量如式(2)所示。

Qvi=nηopLptWptIb

(2)

式中:Qvi为真空管内管获得的太阳能量,W;ηop为集热器光学效率;n为集热器集热单元个数。

真空管外管获得的太阳辐射如式(3)所示。

Qvo=nAptIbτgαvoρ

(3)

式中:Qvo为真空管外管获得的太阳能量,W;Apt为抛物槽总开口面积,m2;τg为玻璃盖板透射率;αvo为真空管外管吸收率;ρ为反射镜反射率。

玻璃盖板获得的太阳辐射如式(4)所示。

Qg=AgIαg

(4)

式中:Qg为玻璃盖板获得的太阳能量,W;αg为玻璃盖板吸收率;I为太阳总辐射,W/m2;Ag为玻璃盖板面积,m2。

集热器腔体内空气获得的太阳能量如式(5)所示。

Qa=AgIτgαa

(5)

式中:Qa为集热器腔体内空气获得的能量,W;αa为空气吸收率。

2.2.2 真空管内管向外耗散的能量

真空管内管以热辐射传递至真空管外管的能量(Qvi,vo,rad)为

(6)

式中:σ为Stefan-Boltzmann常数,5.67×10-8W/(m2·K4);εSAC为选择性吸收涂层发射率;εvo为真空管外管发射率。

真空管内管以对流换热方式传递至真空管外管的能量(Qvi,vo,cov)为

Qvi,vo,cov=nπDviLvihvi,vo(Tvi-Tvo)

(7)

式中:hvi,vo为真空管内管与外管间的对流换热系数,W/(m2·K)。

根据真空管内压力的变化,hvi,vo有2种不同的计算式[15]。当真空管内压力<0.013 Pa时,对流换热形式为自由分子换热,hvi,vo计算式为

(8)

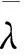
当真空管内压力≥0.013 Pa时,hvi,vo计算式为

(9)

式中:kvi,vo为真空管间气体导热系数,W/(m·K);Prvi,vo为真空管内管与周围气体平均温度条件下的普朗特数;Ravi为瑞利数。

真空管外管以对流换热方式传递至集热器腔体内空气的能量(Qvo,a,cov)为

Qvo,a,cov=nπDvoLvohvo,a,cov(Tvo-Ta)

(10)

式中:hvo,a,cov为真空管外管与空气对流换热系数,W/(m2·K)。

由于集热器腔体内空气流动几乎静止,故hvo,a,cov的计算式为

(11)

式中:λa为集热器腔体内空气导热系数,W/(m·K);Ravo为真空管外管与周围空气的瑞利数;Prvo,a为真空管外管与腔体内空气平均温度条件下的普朗特数。

真空管外管以热辐射方式传递给玻璃盖板的能量(Qvo,g,rad)为

(12)

腔体内空气以对流换热方式传递至玻璃盖板的能量(Qa,g,cov)为

Qa,g,cov=Agha,g,cov(Ta-Tg)

(13)

式中:ha,g,cov为腔体内空气与玻璃盖板间的对流换热系数,W/(m2·K)。

ha,g,cov计算式为

ha,g,cov=2.8+3v

(14)

式中:v为风速,m/s。

玻璃盖板以对流换热方式向周围环境散发的能量(Qg,amb,cov)为

Qg,amb,cov=Aghg,amb,cov(Tg-Tamb)

(15)

式中:hg,amb,cov为玻璃盖板与环境间的对流换热系数,W/(m2·K),hg,amb,cov计算式与式(14)相似,仅与风速相关。

玻璃盖板以热辐射向天空发射的能量(Qg,sky,rad)为

(16)

式中:εsky为天空热辐射率,为0.796[16];εg为玻璃盖板热辐射率。

2.2.3 真空管内管向内传递的有用热能

真空管内管以对流换热方式传递给热管蒸发段的能量(Qvi,e,cov)为

Qvi,e,cov=nπDviLvihvi,e(Tvi-Te)

(17)

式中:Lvi为真空管内管长度,m;hvi,e为真空内管与热管蒸发段间对流换热系数,W/(m2·K),其计算式与式(8)相似。

热管蒸发段传递给热管冷凝段的能量(Qhp)为

Qhp=n(Te-Tc)/Rhp

(18)

式中:Rhp为热管等效热阻,K/W;

热管冷凝段以对流换热传递给流体工质的能量(Qf)为

Qf=nπDcLchc,f(Tc-Tf)

(19)

式中:hc,f为热管冷凝段与流体工质对流换热系数,W/(m2·K),其参数由丘吉尔-朋斯登公式确定[17]。

根据式(2)—(19),集热器一维稳态热力学模型为

(20)

3 集热特性分析

3.1 归一化热效率

根据上述集热器一维稳态数学模型,通过MATLAB软件对集热器热效率进行求解计算。根据文献可计算得集热器年均光学效率为57.6%[14,18],以此为基础可获得集热器热效率变化规律。图3为不同集热器归一化热效率,所设计集热器归一化曲线计算式为[19]

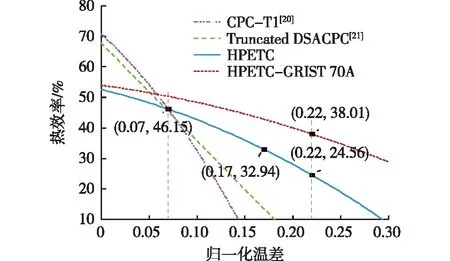
图3 集热器归一化热效率Fig.3 Normalized thermal efficiency of collector

ηth=52.57-75.16T*-237.00(T*)2R2=0.99

(21)

式中:T*为归一化温差,T*=[(Tout+Tin)/2-Tamb]/Ib,Tout和Tin分别为集热器出口和进口温度;R2为拟合度。

由图3可知:由于集热器温度升高,归一化温差也越大,热损失越大。当工作温度为473.15 K时,热效率为32.94%,此时T*=0.17。当T*=0.22时,集热器工作温度为523.15 K,热效率从峰值52.57%下降为24.56%。相比于其他聚光器如CPC-T1型[20]和Truncated DSACPC型[21],当T*>0.07时,集热器热性能比其他2种聚光器更佳。

3.2 热阻分析

由图3还可知:集热器吸收的太阳能量分为向传热流体传递的有用能和对外损失的能量。有用能传递方向的热阻越小、热损方向的热阻越大,有利于集热器热性能的提高。为优化集热器热性能,在风速为1 m/s、环境温度为290 K和流体质量流量为0.02 kg/s的情况下,研究了直射辐射、进口温度、真空管内压力及SAC发射率对传热过程中的4种热阻(Rvi,e,cov、Rvi,vo,rad、Rvi,vo,cov和Rg,sky,rad)的影响。

为求解集热器热阻,根据热阻与热量之间的关系式(式(22))进行求解计算。

(22)

式中:Q为热量,W;A为面积,m2;R为热阻,K/W;ΔT为温差。

3.2.1 太阳直射辐射对热阻的影响

图4为太阳直射辐射对4种热阻的影响变化曲线。由图4可以发现:随着太阳辐射的增大,Rvi,e,cov、Rvi,vo,rad和Rg,sky,rad逐渐减小,这是由于随着太阳辐射的增大,真空管内管获得的太阳能量增大,内管温度升高。当进口温度不变时,真空管内管与热管蒸发段间的温差增大,导致两者间的对流换热加强,从而导致Rvi,e,cov减小;Rvi,vo,rad也由于真空管内管温度的升高,导致热辐射损失加剧,从而导致玻璃盖板从真空管处获得的能量增大,对外辐射损失增大,Rg,sky,rad减小。但是在不同进口温度下,进口温度越高,Rvi,e,cov越大,Rvi,vo,rad则相反,这是由于热管具有等温性,当集热器正常工作时,蒸发段和冷凝段温度几乎相同,故当进口温度越高时,热管蒸发段温度也越高,这就缩小了真空管内管与蒸发段间的温差,导致两者间换热减小。在保持太阳直射辐射一定时(即获得的能量相同时),由于真空管内管向热管传递的能量减少,为保持热平衡,真空管内管温度上升,热辐射损失增大,Rvi,vo,rad减小。

图4 太阳直射辐射对热阻的影响Fig.4 Effects of direct solar radiation on thermal resistance

由于上述原因,导致真空管内管温度提升,真空管环形区域分子间平均碰撞自由程变大,又根据式(8)计算可知,管内对流换热系数变小,故Rvi,vo,cov随直射辐射的增大而不断增大,进口温度越大,热阻越大。

3.2.2 进口温度对热阻的影响

图5为进口温度对4种热阻的影响变化曲线。由图5可知:Rvi,e,cov和Rvi,vo,cov随进口温度的升高而不断增大,其中Rvi,vo,rad的变化最为显著。当直射辐射为600 W/m2、进口温度为500 K时,热阻相较300 K时降低了约77.40%。Rvi,vo,cov随进口温度增大而增大,其变化程度仅次于Rvi,vo,rad,主要原因是真空管内压力很小,为分子自由换热,辐射热阻对温度的敏感性较对流换热热阻更大。

图5 进口温度对热阻的影响Fig.5 Effects of inlet temperature on thermal resistance

3.2.3 真空管内压力对热阻的影响

图6为真空管内压力对4种热阻的影响变化曲线。由图6可知:整体上,真空管内压力主要对Rvi,vo,cov和Rvi,vo,rad的影响较大,这是由于当真空管内压力<0.013 Pa时,真空管间对流换热形式为分子自由换热,此时4种热阻数值基本相同。因此,在真空管制造过程中,其真空管内压力要求<0.01 Pa即可。

图6 真空管内压力对热阻的影响Fig.6 Effects of vacuum pressure on thermal resistance of vacuum tube

3.2.4 SAC发射率对热阻的影响

图7为SAC发射率对4种热阻的影响变化曲线。由图7可知:SAC发射率对真空管间的辐射热阻影响最大,并且随着SAC发射率的提高,Rvi,vo,rad下降趋势也逐渐平缓。由式(6)和(22)可知:SAC发射率与Rvi,vo,rad呈倒数关系,发射率越大,热辐射损失越大,热阻越小,且随着SAC发射率增大,Rvi,vo,rad整体的变化趋势降低。另外,随SAC发射率增大,进口温度对Rvi,vo,rad的影响降低。

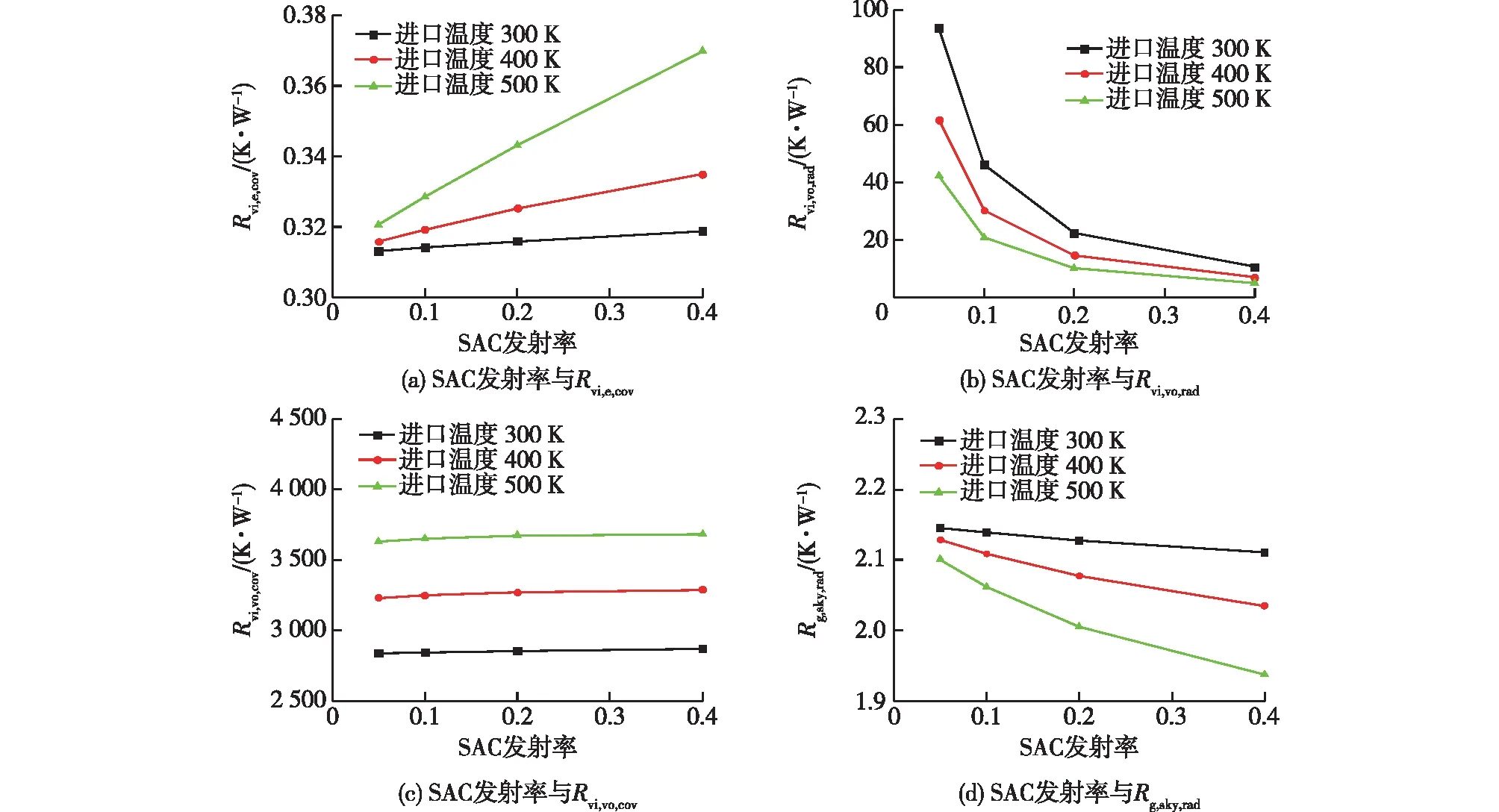
图7 SAC发射率对热阻的影响Fig.7 Effects of SAC emissivity on thermal resistance

3.3 方差分析

为了减少模拟次数,同时全面了解各因素对热性能的影响规律[22],采用方差分析法对上述4种因素进行分析。采用表2数据进行分析,根据正交实验设计原则,选择L9(34)型方案,使用SPSS软件完成正交实验设计,结果如表3所示。

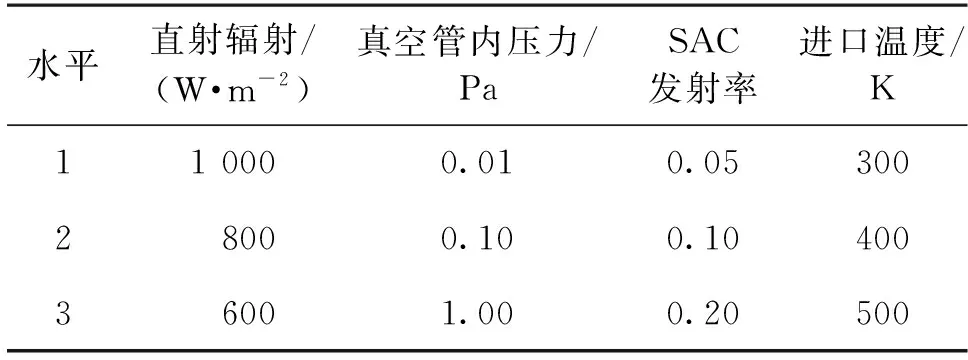
表2 因素水平Table 2 Factors and levels

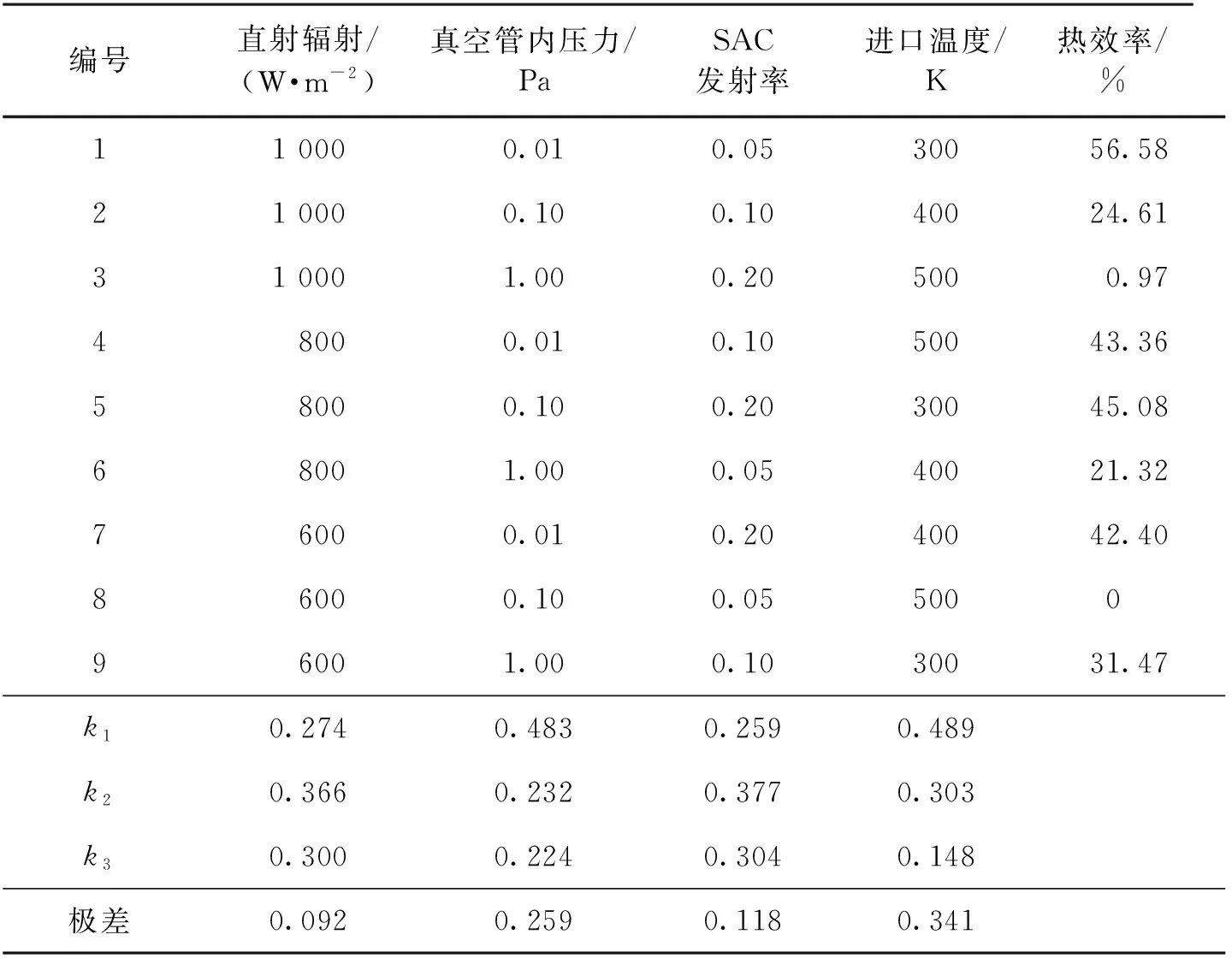
表3 正交实验结果及分析Table 3 Orthogonal test results and analysis

由方差分析中的极差大小可知该列对应的影响因素对集热器热效率影响程度的高低,数值越大,影响程度越高。由表3可知:4种因素对热效率的影响程度由高到低排列为进口温度、真空管内压力、SAC发射率、直射辐射。试验中的最佳组合方式:直射辐射为800 W/m2、真空管内压力为0.01 Pa、SAC发射率为0.1和进口温度为300 K,此时集热器热效率为56.00%,热阻分别为Rvi,e,cov=0.3 K/W、Rvi,vo,rad=557.4 K/W、Rvi,vo,cov=2 755.8 K/W、Rg,sky,rad=0.5 K/W。由图3还可知:当真空管内压力为0.01 Pa时,若是将黑铬涂层替换为低发射率的GRIST 70A涂层,集热器热效率可得到大幅提升。当T*=0.22时,使用GRIST 70A涂层的集热器(HPETC-GRIST 70A)热效率比使用黑铬涂层的集热器提升了约13.45%,可达到38.01%。

4 实验验证

为了验证上述一维稳态数学模型的正确性,搭建了集热器实验平台。集热器安装方式与理论条件一致,结构参数与表1相同。为了测量环境温度、风速和太阳直接辐射,配备了一台精密气象站(Kipp &Zonen公司生产)。采用多路温度巡检仪(常州Applent Instruments Ltd.生产,AT4516型)监测歧管进出口的流体温度。蠕动泵(Kamoer生产,DIPump 550-B163型)可维持流体循环流量,并调节其在收集器中的流量。恒温水浴槽(HH-2,国旺)能够使进口流体在一定范围内恒温流入。试验平台如图8(a)所示。

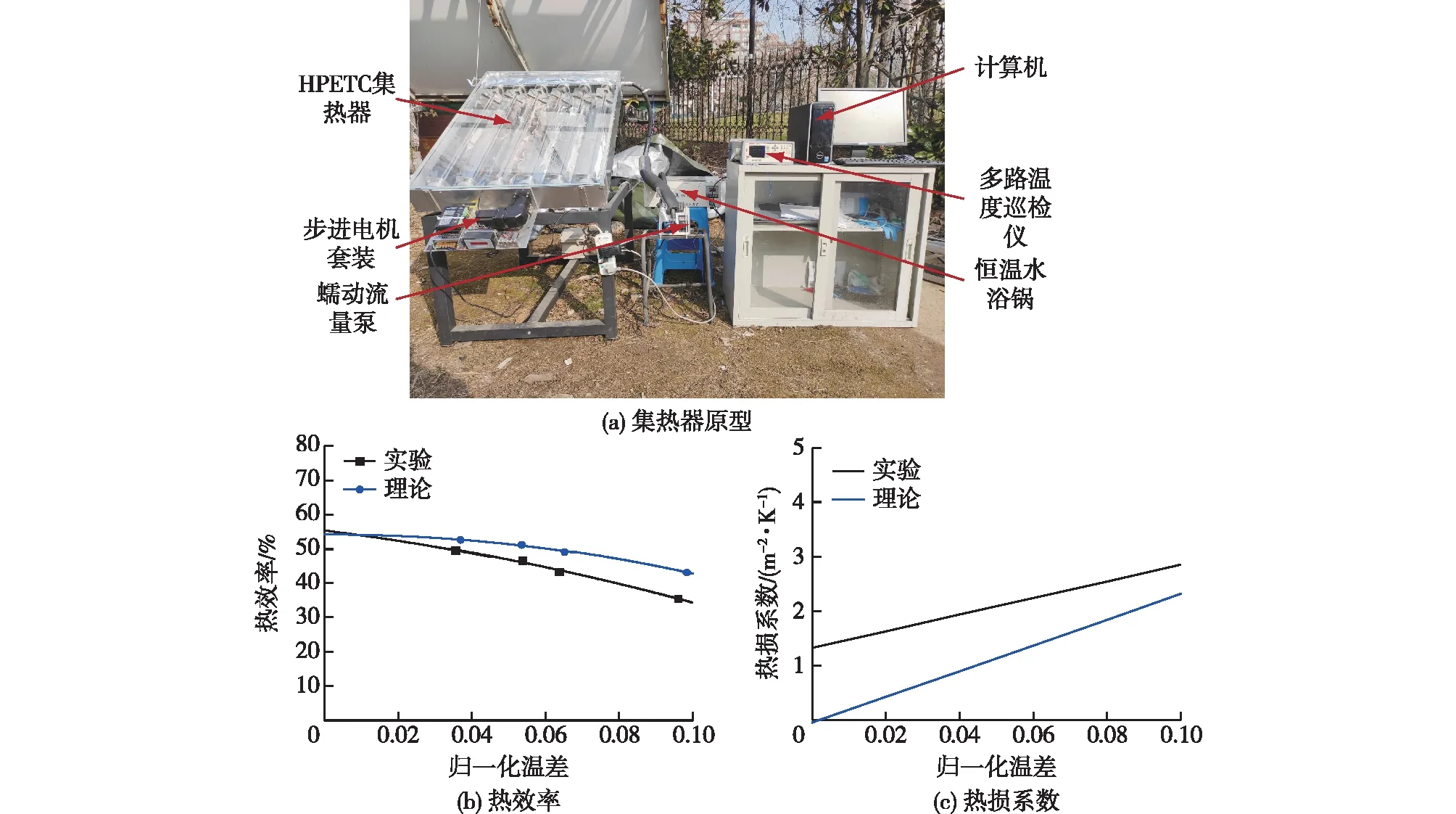
图8 集热器实验平台及理论与实验结果对比Fig.8 Experimental platform, comparison of theoretical and experimental results of collector

根据测试标准《太阳能集热器热性能试验方法(GBT 4271—2007)》[19],对集热器热性能进行评估。实验于2022年1月16日至1月19日上午9时至下午14时进行,并将实际条件下的理论与实验结果进行比较(图8(b))。经测试,使用的镜面铝反射镜的反射率为0.94、玻璃盖板透射率为0.94、真空管透射率为0.92、高温除氧后的热管蒸发段吸收率和发射率分别为0.88及0.72(293.15 K)。由于缺少可商用的SAC,吸收器表面并未涂有SAC,故需调整集热器光学和热力学模型:吸收器由真空管内管变为热管蒸发段。调整后的热力学模型计算式为

(23)

式中:Qc为热管蒸发段吸收的太阳能量,W;Qvi为真空管内管吸收的热量,W。

Qvi计算式为

Qvi=nAptIbτgτvoαviρ

(24)

式中:Apt为抛物槽总开口面积,m2;τg为玻璃盖板透射率;τvo为真空管外管透射率;αvi为真空管内管吸收率。

由图8(b)和8(c)可知:总体而言,理论结果与实验结果趋势相似,平均相对误差为4.8%,验证了理论模型的准确性。误差来源:①集热器箱体与环境之间存在一定热交换;②抛物槽难以小批量制造,导致聚光精度较低,并存在一定的安装误差;③理论计算时未考虑真空管端部热损失;④理论计算的蒸发段发射率为定值,实际情况下发射率随温度升高而变大;⑤实验存在一定测量误差。

实验与理论误差随着归一化温差的增大,误差差距不断增大。拟合后的归一化曲线斜率为集热器吸热体对环境空气的总热损系数,根据文献可知,热损系数与热阻呈倒数关系[23-24]。因此,总热损系数越大,集热器能量对外损失过程中的热阻越小,这就导致损失的能量越多,热损失越严重。当太阳直射辐射和环境温度一定时,进口温度越高(即T*越大),总热损系数增大,集热器总热阻随之减小,热损失不断加大;而当进口温度与环境温度一定时,直射辐射越小,集热器热效率越大,这表明:在当其他条件一定时,集热器的真空管内管与外部环境间的总热阻随太阳直射辐射的降低而增大。

5 结论

本文设计了一种厚度仅124.5 mm的紧凑型热管真空管太阳能集热器,可有效与建筑结合;为分析该集热器热性能,建立了一维稳态传热模型,并利用该模型对集热器传热特性进行分析;搭建了实验平台,对理论模型进行了验证。结论如下:

1)当T*=0.22时,集热器工作温度为523.15 K,热效率为24.56%。当T*>0.07时,所设计集热器比CPC-T1和Truncated DSACPC型集热器具有更高的热效率。

2)随着太阳辐射的增大,热管蒸发段与真空管内管间对流换热热阻、玻璃盖板与天空间的辐射热阻和真空管内管与外管间辐射热阻逐渐减小,真空管内管与外管间的对流换热热阻则不断增大;其他条件保持一致下,进口温度对真空管内管与其外管间辐射热阻的影响最为显著;当真空管内压力<0.01 Pa时,其变化对传热热阻无明显影响;SAC发射率对真空管间的辐射热阻影响程度最大,并且随着SAC发射率的提高,真空管内管与其外管间辐射热阻下降趋势也逐渐平缓。

3)4种因素对集热器热效率的影响程度从小到大排列为直射辐射、SAC发射率、真空管内压力、进口温度。当真空管内压力为0.01 Pa时,集热器选用发射率更小的SAC(GRIST 70A),其热效率比使用黑铬涂层的集热器提升了13.45%,为38.01%(T*=0.22、T=523.15 K)。

4)所设计集热器结构简单、厚度薄、易与建筑屋面结合,同时集热温度高,具有较高热效率(T=523.15 K,ηth=24.56%),可为建筑(空调)和工业过程提供中温热能。