混杂纤维发热格栅增强砂浆/混凝土板力学性能

周竞洋,汪 昕,梁训美,赵纯锋,沈君乾

(1.东南大学 土木工程学院,江苏 南京 211189;2.山东路德新材料股份有限公司,山东 泰安 271000)

冬季道路积雪结冰会导致路面的静摩擦因数和车辆的附着能力降低,进而影响车辆的制动性[1]。常用的路面融雪化冰方法有人工/机械除雪、化学融雪、地热法和电热法等[2-5]。人工/机械除雪对人力、物力的需求较大且存在滞后性,很难快速清除路面积雪。化学融雪法会缩短道路使用寿命,并造成地下水污染。而地热法和电热法是通过加热路面的方式融化冰雪,具有快速和环保的优点。除了地热法受地区限制较大之外,电热法是目前研究和实际使用较多的方法。电热法的发热部件类别主要包括发热线、发热电缆、发热筋、导电混凝土、碳纤维发热格栅等。相比传统金属发热材料,碳纤维发热格栅具有发热快、电磁辐射量极小、热转化率高、能耗低以及寿命长等优点。

Zhao等[6]研究了混凝土路面中布置碳纤维发热线的融雪化冰方法,得到了发热线间距为0～100 mm时能够满足路表温度分布均匀性的要求。Cevallos等[7]将碳纤维发热线埋置于桥面铺装层之间进行融雪化冰,提出碳纤维埋置于上下面层之间和埋设间距为8～10 cm时方案合理。李炎锋等[8]制作了面积为1 000 mm×1 000 mm、发热功率为270 W/m2的道路发热电缆模型,结果表明:发热电缆的输出功率达到250～350 W/m2时,可以满足北京地区路面融雪化冰要求。陈龙等[9]研究了网格尺寸为25 mm×25 mm的内置碳纤维/玄武岩纤维格栅混凝土薄板电热路面模型。通过升温试验发现,在环境温度为-16 ℃左右时,电功率需在400 W/m2以上时,才能满足升温和节约电能的要求,并保持电阻和电功率稳定。Dantino等[10]研究了网格尺寸为10 mm×10 mm的碳纤维/玻璃纤维混合编织网增强混凝土小板,通过小板升温试验发现:在多次升温/降温循环中,小板的电阻率波动范围控制在4.5%以内;30 mm×30 mm网格尺寸以内的小板发热均匀性随网格尺寸的减小而提高。

综上,基于碳纤维良好的发热性能,碳纤维发热元件用于路面融雪化冰具有现实可行性。而混杂纤维发热格栅在一定电功率下具有稳定的发热能力,力学性能优异,兼具经济性,满足路面融雪化冰的要求[11-12]。然而,现阶段对于碳纤维涂层和混杂纤维发热格栅编织形式的研究过于单一,存在重交通荷载或较大变形下对碳纤维保护有限,格栅固化后不易盘卷等局限[13-14];同时,对于碳纤维本身力学性能及力阻效应、混杂纤维发热格栅在不同工程材料中的力学及电阻表现研究较少,不利于混杂纤维发热格栅的推广利用[15-18]。

以混杂纤维发热格栅为研究对象,探究其与砂浆、混凝土这两种常用水泥基材料的界面黏结性能。分别选取砂浆薄板和混凝土板模拟格栅在建筑墙面板和路面上面层使用场景,研究混杂纤维发热格栅对这两种基体板件弯曲性能的影响及受力过程中电阻的变化,验证混杂纤维发热格栅在建筑墙面板和路面结构中应用的可行性。

1 试验材料及方法

1.1 原材料

水泥砂浆和C30混凝土的配合比见表1,其28 d标准抗压强度分别为53.8和32.1 MPa,水胶比分别为40%和50%。玄武岩纤维格栅由浙江石金玄武岩纤维股份有限公司提供,基本参数见表2。碳纤维束采用日本东丽公司生产的T700碳纤维无捻粗纱,基本参数见表3。碳纤维发热芯为手工制备的聚氨酯树脂有捻碳纤维浸胶纱。

表1 水泥和混凝土的配合比Table 1 Mix proportion of cement and concrete kg/m3

表2 玄武岩纤维格栅性能参数Table 2 Performance parameters of basalt fiber textile

表3 T700碳纤维性能参数Table 3 Performance parameters of T700 carbon fiber

1.2 格栅拉拔性能测试方法

试验设计了3种变化参数,分别为2种基体(砂浆和混凝土,分别以M和C表示),3种埋入深度(15、30和55 mm)和3种碳混杂率(0%、50%和100%),每种工况均制备3组试件。基体为边长70.7 mm的立方体。格栅为300 mm×50 mm的矩形,且在基体中居中放置。碳纤维发热芯长度为300 mm。碳混杂率是通过浸胶纱的根数定义,如50%碳混杂率格栅是将碳纤维浸胶纱固定在1支玄武岩格栅上,另1支保持原状(图1)。加载设备为日本岛津AG.x plus万能试验机。试验加载速度参考文献[19],取1.2 mm/min。基体通过辅助工装固定,格栅自由端采用铸铁片锚固。试验终止条件为格栅拔出或拉断。格栅与基体之间的黏结应力按照平均值计算。

图1 碳纤维发热芯与玄武岩纤维格栅Fig.1 Carbon fiber heating core and basalt fiber textile

1.3 格栅增强砂浆/混凝土板弯曲性能测试方法

弯曲试验参数包括板类型(砂浆板(MP)和混凝土板(CP)),碳混杂率(0%、50%和100%)以及加载方式(静力和往复加载)。砂浆薄板的尺寸为300 mm×100 mm×20 mm,相应的格栅尺寸、格栅截面配筋率和格栅体积配置率分别为480 mm×100 mm、0.2%和0.4%。混凝土薄板的尺寸为400 mm×150 mm×40 mm,相应的格栅尺寸、格栅截面配筋率和格栅体积配置率分别为480 mm×150 mm、0.1%和0.2%。格栅在两种板内为居中放置。值得注意的是,砂浆板和混凝土板的尺寸并不相同,这是因为砂浆板的设计用于墙体,而混凝土板的设计用于混凝土路面。图2为砂浆板和混凝土板的加载示意图。由图2可知:碳纤维浸胶纱的长度与两种格栅的长度一致。当静力加载速度为1 mm/min时,试验过程中出现以下情况认为板件发生破坏:①板中格栅被拉断;②板件顶部受压区基体被压碎挤出;③板件挠度过大,不适于继续承载;④荷载下降至极限荷载的85%以下。往复加载方案参考文献[20],目的是测试碳纤维发热芯在往复荷载作用下的稳定性。对碳混杂率分别为50%和100%的玄武岩纤维格栅增强混凝土板进行往复试验,终止次数和加载频率分别为20 000次和1 Hz。当碳混杂率为50%时,荷载上限和下限分别为0.496fu和0.147fu,fu为板的极限拉伸强度;当碳混杂率为100%时,荷载上限和下限分别为0.493fu和0.145fu。

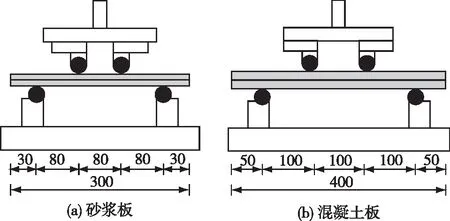
图2 砂浆板和混凝土板的加载示意图(mm)Fig.2 Loading diagram of mortar and concrete slabs (mm)

板跨中名义最大弯曲应力可按式(1)计算。

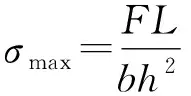
(1)

式中:σmax为板跨中名义最大弯曲应力,MPa;F为板最大荷载,N;L、b和h分别为板的跨度、宽度和厚度,mm。

板的延性系数计算方法参考文献[21],可按式(2)计算。

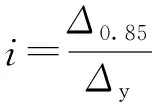
(2)

式中:i为延性系数;Δy为荷载-位移曲线的第1次屈服位移,由经过最大荷载的水平线与加载段切线的交点确定,mm;Δ0.85为荷载下降到85%极限荷载时对应的跨中位移,mm。

2 试验结果与分析

2.1 格栅界面黏结性能

2.1.1 破坏模式

图3为3种玄武岩纤维格栅增强砂浆拉拔试件破坏模式。由图3可知:当埋入深度为15、30和55 mm时,50%碳混杂率格栅增强砂浆拉拔试件的拔出模式均显示为1支格栅完整拔出和另1支格栅拉断2种拔出模式,这是由于部分节点处使用树脂黏结碳纤维后增强了格栅的锁嵌能力,且增大了黏结处的接触面积,使得50%碳混杂率格栅的2支格栅受力不均。混杂碳纤维格栅的1支承受拉拔力过大,导致碳纤维发热芯和部分格栅基材拉断。当埋入深度为15和30 mm时,100%碳混杂率格栅增强砂浆拉拔试件的拔出模式为完整拔出。当埋入深度为55 mm时,拔出模式分为完整拔出和格栅拉断2种拔出模式。100%碳混杂率格栅相比50%碳混杂率格栅的节点黏结强度和树脂面积均更大,但是由于2支格栅承受拉拔力比较均匀,当埋入深度为15和30 mm时,均为完整拔出模式;当埋入深度为55 mm时,由于埋入太深,格栅和基体的界面黏结力超过了格栅的承载力,部分试件出现了2支均被拉断的现象。

图3 3种玄武岩纤维格栅增强砂浆拉拔试件破坏模式Fig.3 Failure modes of three types of basalt fiber textile reinforced mortar slabs

图4为3种玄武岩纤维格栅增强混凝土拉拔试件破坏模式。由图4可知:玄武岩纤维格栅增强混凝土与砂浆拉拔试件的拔出情况类似,均为完整拔出。对于50%碳混杂率格栅增强混凝土拉拔试件,当埋入深度为15和30 mm时,其失效模式与砂浆拉拔试件拔出模式一致,55 mm埋入深度没有完整拔出的试件,且发生了格栅整体被拉溃的拔出现象。对于100%碳混杂率格栅增强混凝土拉拔试件,3种埋入深度破坏模式与50%碳混杂率格栅的破坏模式一致,55 mm埋入深度也出现了格栅整体被拉溃的现象,说明随着基体粒径的增大,格栅锁嵌作用得到进一步发挥。

图4 3种玄武岩纤维格栅增强混凝土拉拔试件破坏模式Fig.4 Failure modes of three types of basalt fiber textile reinforced concrete slabs

2.1.2 界面黏结性能

通过排水法得到纬向玄武岩纤维格栅1支的周长为10.74 mm,聚氨酯树脂基有捻型碳纤维增强复合材料(CFRP)浸胶纱的周长为4.84 mm。在计算平均黏结应力时,忽略经向格栅的表面积和树脂黏结处树脂的表面积。2种基体拉拔试件的极限荷载、破坏模式和平均黏结应力如表4所示。由表4可知:荷载随着碳混杂率和埋入深度的增大而增大。当碳混杂率相同时,平均黏结应力总体上随着埋入深度的增大而减小;当埋入深度相同时,黏结应力总体上随着碳混杂率的增大而增大。

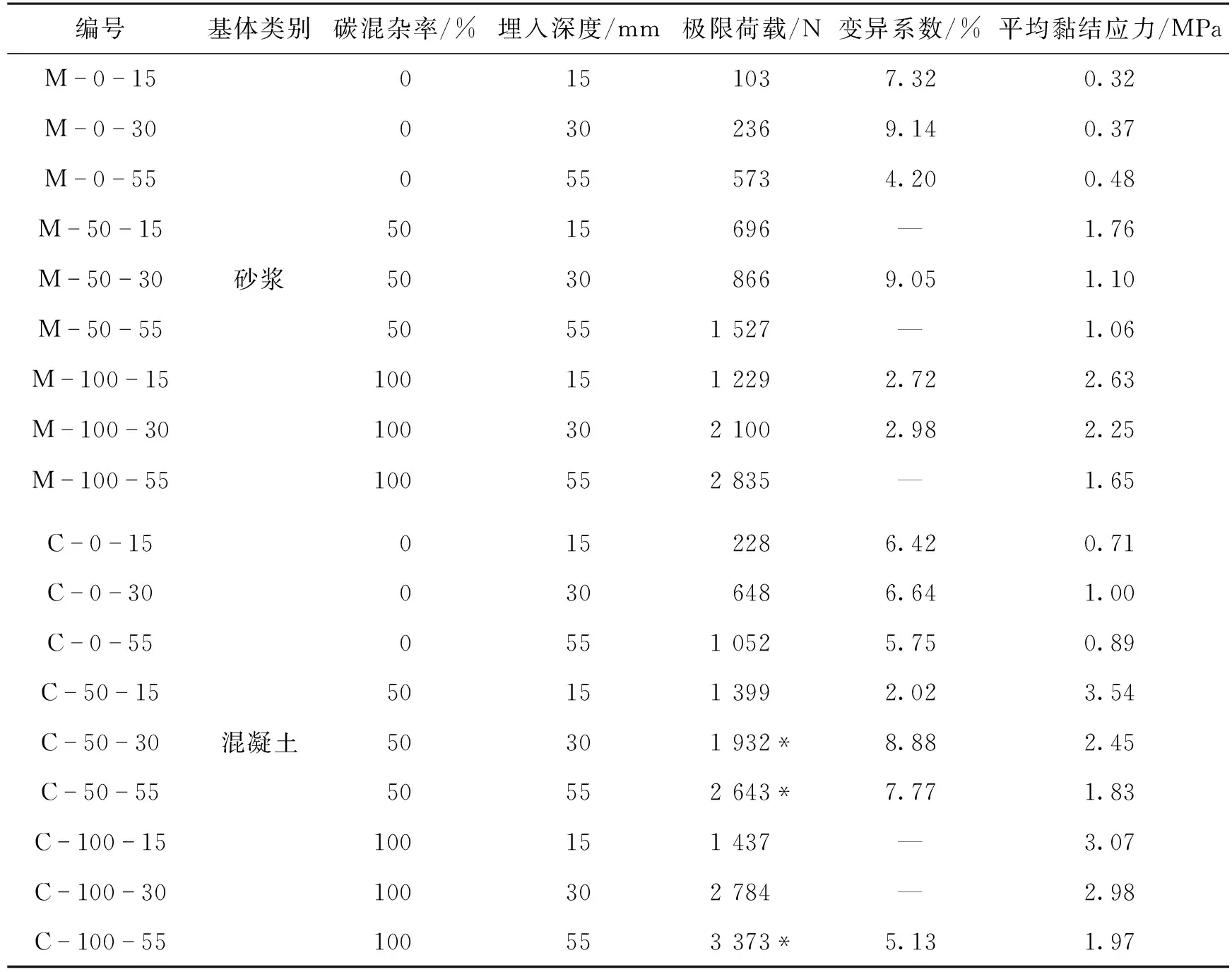
表4 拉拔试验结果Table 4 Results of pullout experiments

图5为2种基体的荷载-位移曲线。由图5可知:加载前期,荷载-位移曲线均出现了初始刚度偏小的现象,这是因为试验开始前未对试件进行预加载导致的。当碳混杂率和埋入深度相同时,2种基体拉拔试件体现出较为相似的变化规律。总体上,拉拔力随滑移先增大后减小。当碳混杂率逐渐增大时,拉拔力-滑移曲线的变化规律会发生显著改变,即曲线出现快速上升和快速下降的趋势。

图6为极限荷载/黏结应力与埋入深度的关系。由图6可知:玄武岩纤维格栅增强砂浆/混凝土试块的极限荷载-埋入深度曲线显示了正相关的增长关系。50%和100%碳混杂率格栅增强砂浆/混凝土试块的荷载增长率逐渐减小,同时黏结应力随埋入深度不断减小。50%碳混杂率格栅增强砂浆试块曲线由于没有收集到30和55 mm埋入深度下完全拔出模式的数据,导致曲线出现不规律的波动;30与55 mm埋入深度下的黏结应力相近。随着碳混杂率的提升,界面平均黏结应力整体水平提升,主要原因在于:① 拔出过程中,部分节点处固定碳纤维发热芯的三悠环氧树脂提高了节点强度,同时增强了格栅对基体的机械嵌锁作用;② 有捻碳纤维发热芯表面粗糙,且和基体黏结良好。此外,格栅与混凝土基体界面黏结应力整体高于格栅与砂浆基体界面黏结应力,这是因为混凝土内的粗骨料粒径大,更能充分发挥格栅的锁嵌作用。随着埋入深度增大,平均黏结应力整体呈下降趋势,这是因为:① 随着埋入深度的增大,受力后的格栅黏结应力分布越不均匀,导致平均黏结应力下降;②当埋入深度为55 mm时,混杂纤维发热格栅试块中有些破坏模式为拉断破坏,此时界面黏结强度超过了格栅极限拉伸强度,导致平均黏结应力下降。

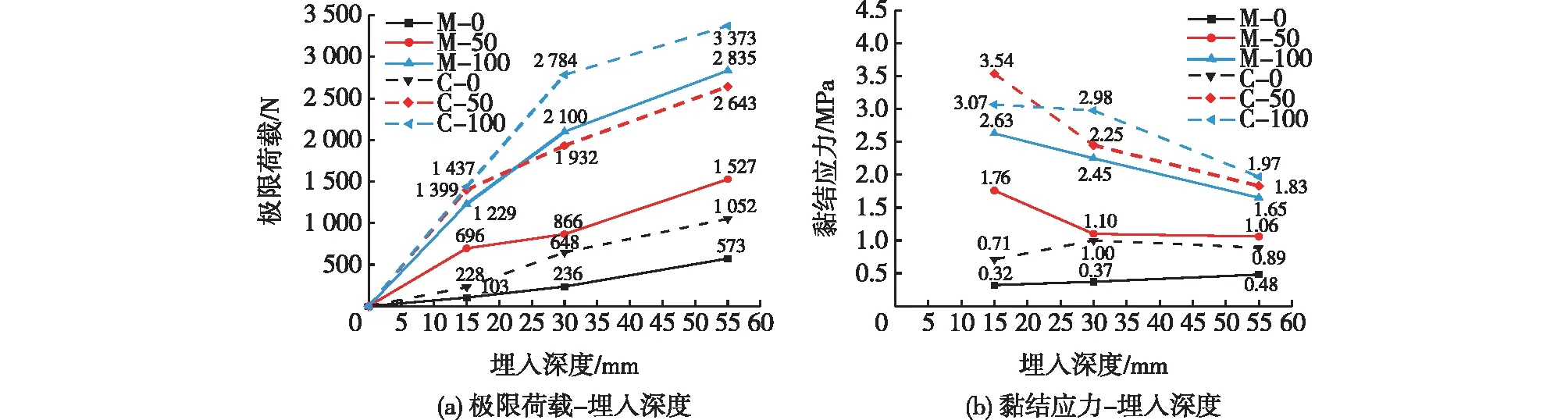
图6 极限荷载/黏结应力与埋入深度的关系曲线Fig.6 Relationship curves between ultimate load/bonding stress and insert depth

2.2 砂浆/混凝土板的静力弯曲性能

2.2.1 破坏模式

4种砂浆薄板的破坏模式如图7—10所示。由图7可知:对于素砂浆板,在加载初期,板体本身无明显变化,位移计示数为0。当荷载达到极限荷载时,板体纯弯段出现1条贯穿裂缝后直接破坏。由图8可知:对于玄武岩纤维格栅增强砂浆薄板,从加载开始至开裂荷载时,荷载-位移曲线呈线性增长。当出现第1条裂缝后,荷载出现一定幅度的下降,此时由于格栅的存在,阻止了裂缝的继续发展,荷载继续上升。若出现第2条裂缝,则重复之前的过程;达到极限承载力后,位移继续增大,荷载保持在极限荷载或在其附近波动,显示出良好的延性。当变形达到板体变形极限后发生破坏,板体纯弯段出现1或2条贯穿裂缝,板顶砂浆被压碎,板底出现1或2条贯穿裂缝,与板顶贯穿裂缝相对应,可以通过贯穿裂缝观测到板内格栅没有明显破坏现象。由图9和10可知:对于混杂纤维发热格栅增强砂浆薄板,其加载情况与玄武岩纤维格栅增强砂浆薄板相似,加载结束后板底纯弯段裂缝更多、更窄,几乎无法通过裂缝观测到板内格栅,这是由于试件的裂缝宽度等于纯弯段内格栅伸长量减去基体的伸长量,当裂缝数量增加时,裂缝宽度减小。

图7 素砂浆板的破坏模式Fig.7 Failure modes of mortar slabs

图8 玄武岩纤维格栅增强砂浆板的破坏模式Fig.8 Failure modes of basalt fiber textile reinforced mortar slabs

图10 100%碳混杂率格栅增强砂浆板的破坏模式Fig.10 Failure modes of mortar slabs with a carbon fiber hybrid ratio of 100%

4种混凝土板破坏模式如图11—14所示。由图11—14可知:格栅增强混凝土板的加载情况及破坏模式与砂浆薄板相似。与砂浆薄板相比,格栅增强混凝土板开裂次数和裂缝数量更多,跨中挠度发展较格栅增强砂浆薄板有所减弱。此外,可以通过板面贯穿裂缝观测到板内部分格栅断裂。

图11 素混凝土板的破坏模式Fig.11 Failure modes of concrete slabs

图12 玄武岩纤维格栅增强混凝土板的破坏模式Fig.12 Failure modes of basalt fiber textile reinforced concrete slabs

图13 50%碳混杂率格栅增强混凝土板的破坏模式Fig.13 Failure modes of concrete slabs with a carbon fiber hybrid ratio of 50%

图14 100%碳混杂率格栅增强混凝土板的破坏模式Fig.14 Failure modes of concrete slabs with a carbon fiber hybrid ratio of 100%

2.2.2 弯曲性能分析

表5为四点弯曲静力试验结果。由表5可知:玄武岩纤维格栅和50%碳混杂率格栅增强薄板开裂荷载较素砂浆板分别提升了5.1%和下降了4.0%,格栅的加入并没有影响砂浆薄板开裂前的弯曲刚度,原因在于:① 格栅截面积相比薄板截面积较小,对于砂浆的削弱效应较弱;② 薄板开裂前,整个截面参与受力,受压区高度较大,格栅铺设在薄板中层,对于纯弯段开裂帮助较小。100%碳混杂率格栅增强薄板开裂荷载较素砂浆板下降了29.3%,这是因为碳纤维发热芯以及粘贴碳纤维发热芯的三悠环氧树脂的截面积削减了部分砂浆板的面积,对基体造成了一定损伤,导致开裂荷载降低,100%与50%碳混杂率格栅增强薄板相比,这一现象更加明显。玄武岩纤维、50%和100%碳混杂率格栅增强薄板较素砂浆板极限承载力分别提升了41.0%、93.9%、141.8%,相应的极限挠度分别提升了72、89和90倍,大幅提高了薄板的受弯变形能力。砂浆板的极限承载力和延性系数随着碳混杂率的增大而增大,其中延性增大的原因在于碳纤维芯需要通过树脂与格栅进行节点黏接,凸出的树脂节点使得格栅不易与砂浆界面发生脱黏和滑移,从而提升了延性。

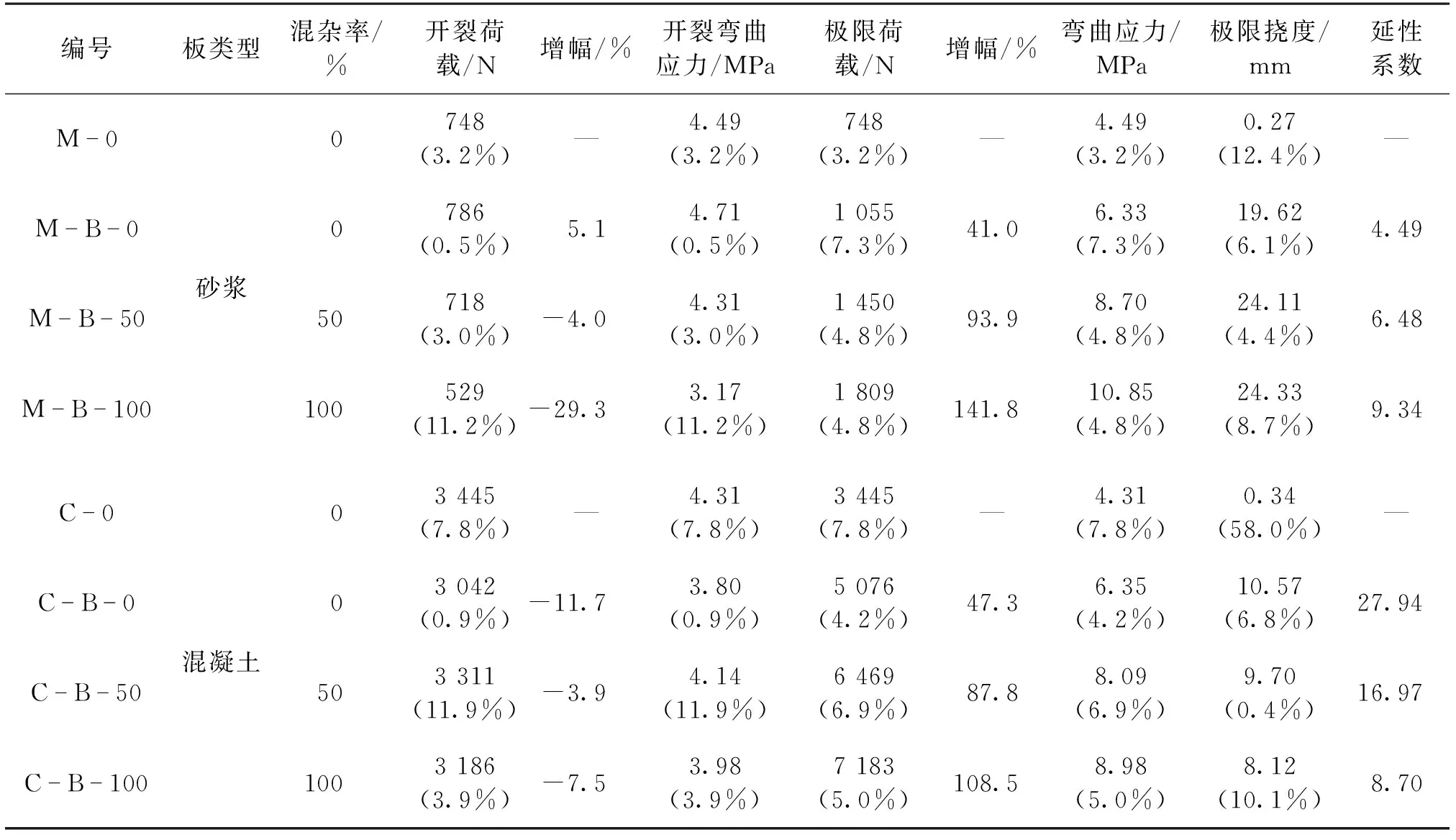
表5 四点弯曲静力试验结果Table 5 Results of four-point bending static experiments

玄武岩纤维、50%和100%碳混杂率格栅增强板较素混凝土板的极限承载力分别提升了47.3%、87.8%和108.5%,相应的极限挠度分别提升了31、28和23倍,大幅提高了混凝土板的受弯变形能力。然而,同种格栅材料增强混凝土板极限挠度小于砂浆薄板极限挠度,这是因为混凝土板中格栅对于提升极限承载力的效果更好。以荷载-跨中挠度曲线包络面积表征结构能量,提升极限承载力越多,极限挠度越小。随着碳混杂率的提升,在混凝土板中混杂纤维格栅各支强度和储存用于变形耗散的能量并没有得到充分发挥,导致在极限承载力上升的情况下,极限挠度下降。格栅增强混凝土板延性系数整体高于格栅增强砂浆薄板延性系数,这是因为铺设1层格栅的情况下,混凝土板与格栅之间的界面黏结强度达到了格栅的极限拉伸强度,格栅变形耗能能力殆尽,导致整体延性水平降低。与格栅增强砂浆薄板不同,随着碳混杂率的提升,格栅增强混凝土板开裂荷载相近,极限承载力提高,极限挠度降低,延性系数不断下降。

图15为砂浆板和混凝土板的荷载-位移曲线。由图15(a)可知:格栅增强砂浆板在初次开裂后,随着变形增大,承载力逐渐提高,达到极限承载力后进入平台段。此时跨中位移不断增大,承载力却没有下降,表明格栅增强砂浆薄板具有良好的延性性能。此时格栅并没有破坏导致荷载突然卸载,也没有达到界面黏结力极限而出现滑移,充分发挥了格栅在砂浆薄板中良好的变形能力。直到部分格栅条带在变形过程中出现损伤或率先达到极限变形而退出工作,荷载才开始下降,此时跨中位移保持平稳发展,并没有出现突然增大的现象。值得注意的是,试件M的加载刚度和开裂荷载与其他工况的结果差异较大,其主要原因在于:① 由于搅拌设备容量较小,导致每次搅拌的砂浆数量只够一种工况使用(每种工况需要制备相同的3组试件),因此,每次搅拌的砂浆可能存在一定的性能差异;② 由于格栅表面较为光滑,易与砂浆之间发生脱黏和滑移,导致加载刚度和开裂荷载略有下降。图15(b)与图15(a)相比,素混凝土的加载刚度和开裂荷载显示了较为合理的结果,这是因为混凝土内部存在一定数量的粗骨料,而粗骨料在格栅孔眼内起到一定的销栓作用,使得格栅较难发生滑移。

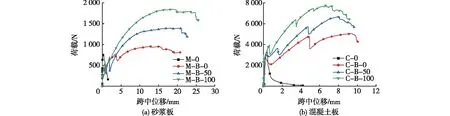
图15 2种板的荷载-位移曲线Fig.15 Load-displacement curves of two types of slabs

2.2.3 力阻效应分析

混杂纤维发热格栅增强砂浆薄板的电阻-跨中位移曲线如图16所示。由图16可知:对于不同的板材而言,混杂纤维发热格栅的电阻几乎不随跨中位移的增大而发生变化,体现了良好的力阻效应。

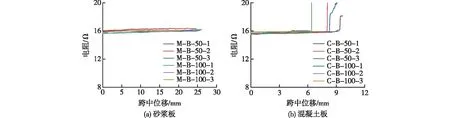
图16 电阻-跨中位移曲线Fig.16 Electrical resistivity-midspan displacement curves

表6为格栅增强砂浆/混凝土薄板的电阻性能。由表6可知:格栅增强砂浆板6根测试碳纤维的最终电阻变化率为0.13%～3.32%,部分碳纤维发热芯变形接近,但未到达聚氨酯树脂有捻型CFRP浸胶纱破坏电阻变化率,表明混杂纤维发热格栅碳纤维发热芯可以在砂浆薄板中承担较大的变形,并且不会在极限承载力附近破坏,可以受到有效保护,50%碳混杂率格栅增强混凝土板3根测试碳纤维全部破坏,100%碳混杂率格栅增强混凝土板3根测试碳纤维有1根破坏、2根在弹性变形范围之内,未破坏碳纤维电阻变化率(保持在1.08%以内),未到达聚氨酯树脂有捻CFRP浸胶纱破坏时电阻变化率。上述结果表明:①100%碳混杂率格栅相比50%碳混杂率格栅,承载力更高的同时各支受力更加均匀;②100%碳混杂率格栅在荷载卸载、跨中位移发展较大时,碳纤维发热芯仍保持良好的变形能力,受到有效保护。

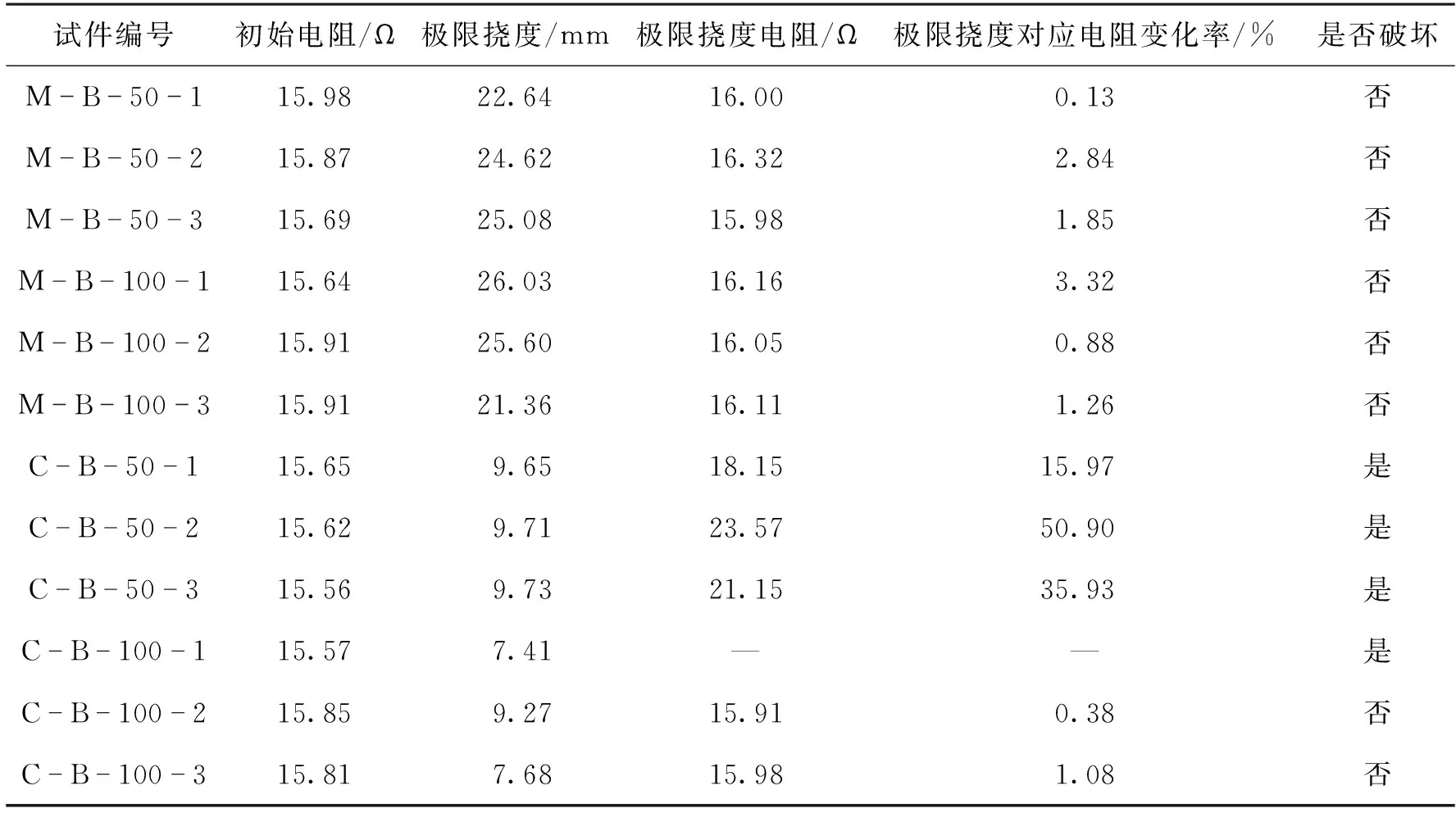
表6 格栅增强砂浆/混凝土薄板的电阻性能Table 6 Electrical resistivity performance of textile reinforced cement/concrete thin slabs

2.3 混凝土板往复荷载下的弯曲性能

2.3.1 往复荷载作用下板的破坏模式

图17为往复荷载下薄板的失效模式。由图17可知:在施加往复荷载前的第1次静载试验中,2个测试板件均出现开裂现象,此时板件底部受弯区出现裂缝,位移计示数显著增大;在卸载阶段,裂缝宽度逐渐减小至接近闭合。静力加载与卸载完成后,板件将开始承受往复荷载。在往复荷载循环中,板件裂缝高度和宽度得到发展,但发展幅度不大。在最后1次静载试验时加载至破坏,破坏模式与之前静力弯曲试验破坏模式相似。

图17 往复荷载下薄板的失效模式Fig.17 Failure modes of thin slabs under repeated load

2.3.2 往复荷载作用下板的弯曲性能

图18为混杂板在不同循环次数下的荷载-跨中位移曲线。由图18可知:首次静载试验中,2种混凝土板均发生了开裂。加载时,在开裂前跨中挠度发展较慢,在2 500～3 000 N范围内混凝土开裂,跨中位移突然增大。随着施加往复荷载的次数增加,跨中位移突然增大的现象会消失,增长速率逐渐放缓,并进入稳步增长阶段。50%和100%碳混杂纤维发热格栅增强混凝土板的跨中位移分别由0增大至1.54和1.59 mm。而当卸载时,板件的跨中位移分别由1.54 mm减小至0.50 mm、1.59 mm减小至0.42 mm,这表明首次静力加载与卸载后板件产生了0.50和0.42 mm的残余位移,主要原因在于受弯段混凝土因开裂出现了不可恢复的变形。然而,在后续循环荷载施加过后,进行静力加载与卸载,薄板的残余位移发展较小,表明此时板件裂缝进入稳定状态,此时2种混杂纤维发热格栅增强混凝土板的跨中位移发展接近,差距较小。

图18 混杂板在不同循环次数下的荷载-跨中位移曲线Fig.18 Load-midspan displacement curves of hybrid slabs under different cycles

图19为50%和100%碳混杂率格栅增强混凝土板的残余强度。由图19可知:20 000次往复荷载循环后,板件跨中位移与5 000、10 000次时较为接近,能够初步认为此时混杂纤维发热格栅的变形趋于稳定,50%和100%碳混杂纤维发热格栅增强混凝土板的残余强度分别为5 968和6 744 N,表明在20 000次往复荷载循环次数下仍有较高的残余强度。

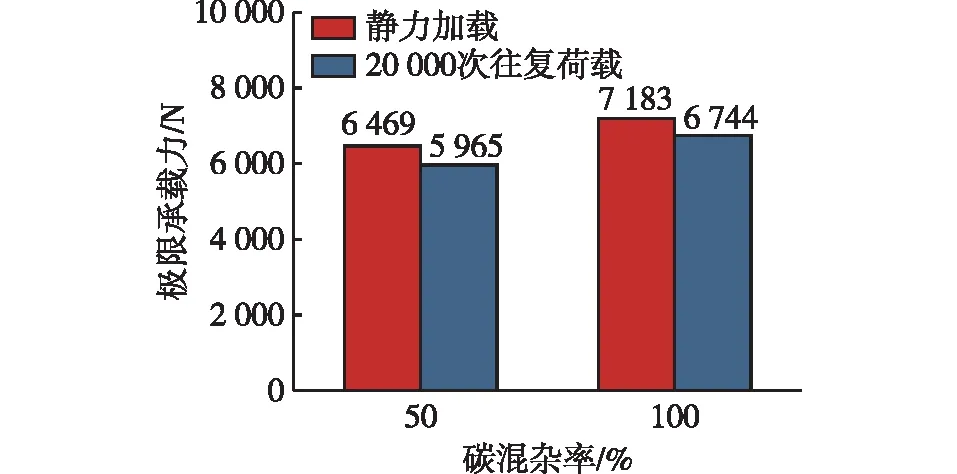
图19 两种混杂板的残余强度Fig.19 Residual strength of two types of hybrid slabs

2.3.3 往复荷载作用下的力阻效应

图20为100%碳混杂率格栅增强混凝土板在不同往复荷载循环次数下的电阻-荷载曲线。由图20可知:碳纤维发热格栅增强混凝土板的测试碳纤维在不同往复荷载循环次数后,其静力加载过程中的电阻几乎没有变化,表明碳纤维发热芯具有较强的抵抗疲劳荷载的能力。其余碳混杂率格栅增强混凝土板的电阻-荷载曲线变化规律类似,故不再赘述。

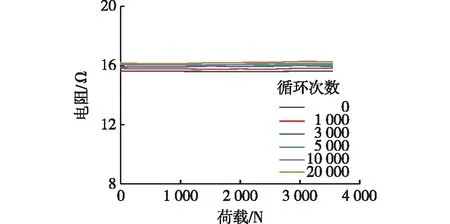
图20 不同往复荷载循环次数下的电阻-荷载曲线Fig.20 Electrical resistivity-load curves under different cycles of reciprocating load

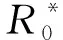
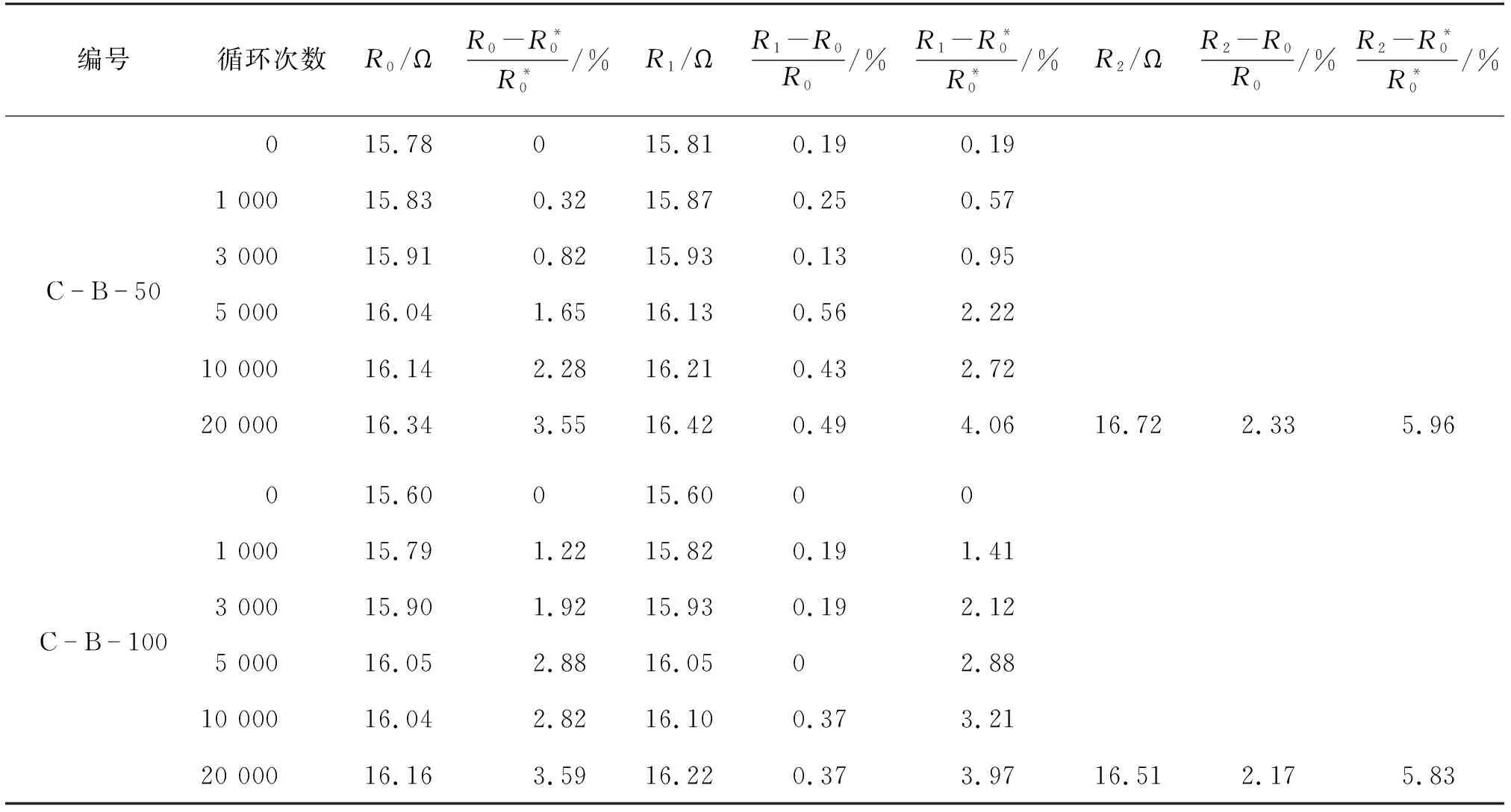
表7 不同循环次数往复荷载作用后静力加载过程中混凝土板的电阻性能Table 7 Electrical resistance performance of concrete slab under static loading after different cycles of reciprocating load

3 结论

本文针对混杂纤维发热格栅在建筑墙面板和路面上面层的使用场景,选用碳混杂纤维发热格栅制作了拉拔增强板件,并进行了黏结性能和弯曲性能试验。

1)相比砂浆基体,混凝土基体更能充分发挥格栅的锁嵌作用,界面黏结应力水平整体高于砂浆基体。随着碳混杂率的提升,有捻碳纤维发热芯粗糙的表面形式以及节点黏结树脂对格栅锁嵌有提升作用,从而提高了界面黏结应力整体水平。随着埋入深度的增大,黏结应力整体呈下降趋势。

2)随着碳混杂率的提升,基体截面受到削弱,两种基体板件开裂弯曲应力呈下降趋势,但是显著提升了极限荷载、极限弯曲应力和延性。100%碳混杂率格栅增强砂浆板极限承载力和极限挠度分别提升141.8%和90倍,而100%碳混杂率格栅增强混凝土板分别提升108.5%和23倍。在静力弯曲试验中,砂浆增强板破坏时碳纤维发热芯未破坏,电阻变化率保持在3.32%以内;混凝土增强板破坏时50%碳混杂率格栅碳纤维发热芯破坏,大部分100%碳混杂率格栅碳纤维发热芯未破坏,电阻变化率保持在1.08%以内。

3)50%和100%碳混杂率格栅增强混凝土板在开裂后产生不可恢复的残余变形。随着循环次数的增加,板跨中位移随荷载缓慢上升,混凝土开裂进入稳定状态。在施加20 000次往复荷载循环后,板件保有较高的残余强度。50%极限荷载水平对应的混凝土增强板跨中位移和电阻变化率趋于稳定。