借助图式辨析,促进概念融通
吴梦媛

【摘 要】“倍”用于描述两个量的比较关系,和乘除法有密切联系,对学生后续学习分数、百分数和比有重要的作用。理解“倍”的概念,图式是直观形象的学习材料。教师可借助图式设置任务,以任务驱动的方式引导学生对点状的知识进行补充、完善,促进学生深度理解“倍”的概念。
【关键词】单元复习;图式辨析;多元表征
单元复习课既要整理、回顾单元知识,关联数学概念,使学生形成知识结构,又要通过练习查漏补缺,使学生完善认知结构。然而,“理”容易枯燥,“练”容易细碎。如何让数学概念的复习既不枯燥又整体关联呢?笔者以人教版教材三年级上册“倍的认识”的单元复习为例,借助图式设置任务,进行复习教学的尝试。
一、解读概念,明晰单元核心内容
以复习数学概念为主的单元复习课一般包括两个层面:一是理解数学概念的内涵本质,二是明晰数学概念的外延关联。“倍”是一种比较关系,与乘除法概念有关联,“倍”的概念直接关联后续学习的“分数”“百分数”“比”等知识。
人教版教材把“倍的认识”作为独立的教学单元进行编排,其意图是让学生在理解“倍”的概念后,运用“倍”的关系解决问题,主要包括“求一个数是另一个数的几倍”和“求一个数的几倍是多少”两种情况。此外,教材还在期末“总复习”中,以图式填空的形式,补充了逆向的“已知一个数的几倍,求这个数是多少”的解决问题。笔者查阅了其他不同版本的教材,发现这些教材也同样凸显了“倍”与乘除法之间的关系,体现了“两个量的倍比”与“两个量相差”的區别。
因此,“倍的认识”单元复习的核心内容,应是深入理解“倍”的概念,凸显基于乘除法概念的比较关系,明晰量与量之间的联系。复习路径为:借助几何直观,抽象概念,把“两个量数的抽象关系”转化为“两个量图的具象关系”。由此,让学生明晰倍数的三个量之间的内部联系,辨析相差关系,延伸包含的倍比关系。
二、分析学情,找准单元知识难点
单元复习课的任务要针对学生的易错点和单元知识的难点设置。学生在学习“倍的认识”单元时,哪些题目容易出现错误?这个单元知识的难点在哪里?针对这些问题,笔者设置了前置式任务,调研了不同班级共247名同学,并对学生的解答情况进行了分析统计。
此次调研中,第一题主要考查学生能否准确描述两个量之间的倍数关系,第二题考查学生能否根据倍数关系准确画出“标准量”和“比较量”,第三题考查学生能否在比较多个量时,排除多余信息,准确写出两个量的倍数关系。调研结果显示,第一题约有87.04%的学生能准确描述两个量之间的倍数关系;第二题第1小题约有87.04%的学生能用图式表示倍数关系,第2小题约有70.04%的学生能用图式表示倍数关系;第三题约有76.92%的学生能正确描述倍数关系。此外,此次前置式任务调研也发现了学生存在的一些典型错误(如图1)。
根据学生的具体解答可以发现,在学完“倍的认识”单元后,学生仍然存在以下问题:(1)对于“倍”的概念的理解不够深入,容易混淆“标准量”和“比较量”;(2)简单认为图式中一共有几份,两个量就是几倍关系;(3)存在见“倍”就“乘”的现象;(4)遇到多个量比较时,难以判断以谁为“标准量”。
三、图式辨析,递推单元核心任务
建立关联是单元复习课的目标之一。基于任务驱动的复习,要把零碎的知识点整合在核心任务中,以图式的形式组建系列任务,改变“提问—回答”的单一互动模式。
(一)再现:借思辨性图式,理解概念本质
在单元复习教学中,教师要借助适切的学习材料,帮助学生再现单元内知识点,梳理知识结构,避免抽象枯燥的重复回顾。用于再现知识的任务情境要能涵盖全单元相关知识,突出教学重难点,帮助学生逐步抽象理解概念本质。
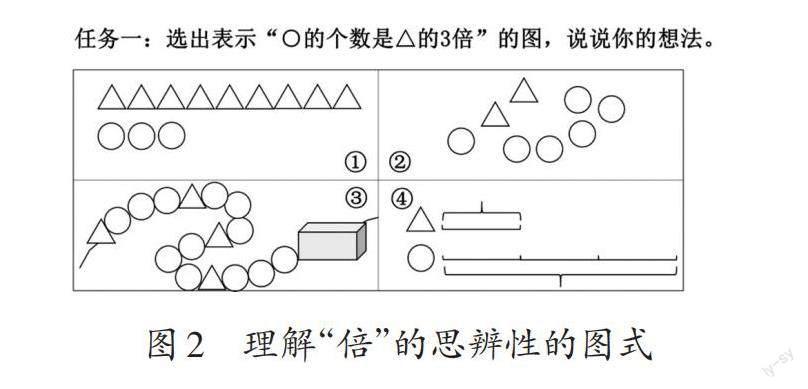
任务一是一组思辨性的图式(如图2),借助该图式能帮助学生进一步理解“倍”的概念。其中,①号图根据学生的易错点区分“标准量”;②号图通过随意摆放,让学生聚焦图形数量,以数量关系理解“倍”的概念;③号图具有思维递进关系,需要学生借助规律得出结论;④号图用线段图来表征“倍”的概念。
学生先独立思考完成任务,然后进行教学反馈。教学反馈时,先反馈正确的图式,概括概念的共性,再辨析错误的图式,强调“标准量”和“比较量”的关系。
“哪些图能表示圆的个数是三角形个数的3倍?”教师先以正确的②号图为例,引导学生回顾“倍”的概念,让学生通过圈一圈、画一画,得出:2个三角形为1份,圆有这样的3份,就可以说圆的个数是三角形个数的3倍。
教师提问:“③号图后面的珠子被盒子挡住了,你是怎么看出圆的个数是三角形个数的3倍的?”启发学生在思辨中理解“△○○○”为一组重复出现的图形,只要观察其中一组就可以推测出倍数关系。
教师追问:“④号图只有两条线段,没有对应的数量,为什么也能表示‘圆的个数是三角形个数的3倍?”引导学生思考:如果三角形表示1,圆有几个?如果三角形有2个、3个、5个……[a]个,圆分别是几个呢?从而渗透函数思想:虽然不知道三角形和圆分别有几个,但圆的个数始终是三角形个数的3倍。比较归纳“倍”概念的本质:正确表示的这三幅图,有什么相同点?
在此基础上,教师提出质疑:“①号图中有9个和3个,为什么不能表示圆的个数是三角形个数的3倍?怎样改就可以了呢?”从而让学生感悟到要找对标准量。由此可知,教学反馈的重点是通过思辨感悟“倍”的概念,从“关注具体数量”走向“关注两个量的关系”。
思辨性图式材料可以帮助学生梳理单元知识,形象化地突破难点,抽象出数学模型。单元复习教学如果用思辨性图式导入,起点较低,学生就会有话可讲。在学生分析图式的过程中,教师要关注学生的语言表述,引导学生先分析标准量,再分析两个量的倍数关系。数学概念的学习过程就是先将具体情境抽象成数学模型,再用自己的语言描述数学模型的过程。在单元复习课中再现知识,有助于学生内化知识,形成自己的认知结构。
(二)关联:借对比性图式,构建知识结构
单元复习教学要关注相似概念的比较,让学生理得清、道得明、悟得透。“倍”与之前学习的“谁比谁多”的数学问题都是用于描述两个量的关系,但“倍”的本质是乘除法结构。借助对比性图式进行复习,可以让学生明晰不同关系的联系和区别。
如图3所示,这是一组对比性图式,用于帮助学生理解“倍”的比较关系。教师呈现图式后,让学生自主列式,然后通过四幅图的两次分类,递进式地展开教学反馈。第一次分类聚焦比较关系。教师提问:“①号图、②号图和④号图都是用乘法或除法表示,③号图为什么是用减法呢?”学生发现,③号图虽然呈现的也是两个量之间的比较关系,但却是“求一个量比另一个量多几”的相差关系,而“倍”是描述乘法的数学模型。第二次分类聚焦“倍”的三个量之间的关系。①号图、②号图、④号图分别对应“求几倍数”“求倍数”和“求一倍数”,从而完善学生对“倍”的理解,帮助学生构建完整的知识结构。
在上述比较的基础上,教师删去表示相差关系的题目,只留下表示倍数关系的三道题目,并提问:“同样是表示倍数关系的三道题,为什么有的用乘法计算,有的却用除法计算呢?”学生比较三道题的对应图式,发现“求几倍数”用乘法,“求倍数”和“一倍数”用除法。接着教师进一步引导学生用“几个几”的乘除法模型进行理解,如④号图是把27平均分成3份,求1份是多少,這“1份数”就是“标准量”,用除法解决。
将对比性图式进行比较,有助于学生以“类”的思想统领概念,促进对概念的理解和迁移。因此,单元复习教学要将新旧知识进行关联,梳理知识脉络,且这种梳理不仅仅是知识的再现,还要在知识再现的基础上进行关联与拓展。
(三)进阶:借综合性图式,促进思维提升
单元复习教学不仅要明晰概念的内涵,还要辨析概念的外延。借助综合性图式关联后续知识,可以延伸知识,促进思维的进阶。
1.选择包含关系的图式,延伸后续知识
“倍”是描述“率”和“比”的基础。如“甲是乙的2倍”还可以说成“乙是甲的[1/2]”“甲和乙的比是2∶1”“乙是甲的50%”等。人教版教材在“倍的认识”这一单元研究的均是两个独立量之间的倍数关系。但实际上,存在包含关系的两个量之间也存在倍数关系,比较常见的是在扇形统计图中用百分数描述倍数关系。
任务三是一组包含性图式(如图4)。教师出示任务三,意图通过变式,帮助学生理解“倍”的比较关系。
教师提问:“你能在图中找到哪些倍数关系?”针对这样的开放性问题,学生会有不同的说法,如“桃树的棵数是梨树棵数的3倍”“男生人数是女生人数的1倍”“女生人数是男生人数的1倍”等。也有一些学生会关注部分与整体的关系,感受到图式的包含关系,发现“果树的总棵数是梨树的4倍,全班人数是女(男)生人数的2倍”。于是教师进一步追问:“反过来,女生人数是全班人数的多少?”学生会想到“一半”或“[1/2]”。这种“一半”或“[1/2]”的表达,表示学生对标准量的理解更进一步,突破了整数倍,为后续学习“一个数是另一个数的几分之几”做了铺垫。
2.递进多个量比较的图式,综合运用知识
利用开放性的素材,设计综合性和挑战性的任务,可以提升单元复习教学的拓展性,具体可以采用条件的开放、问题的开放和方法的开放等方式。
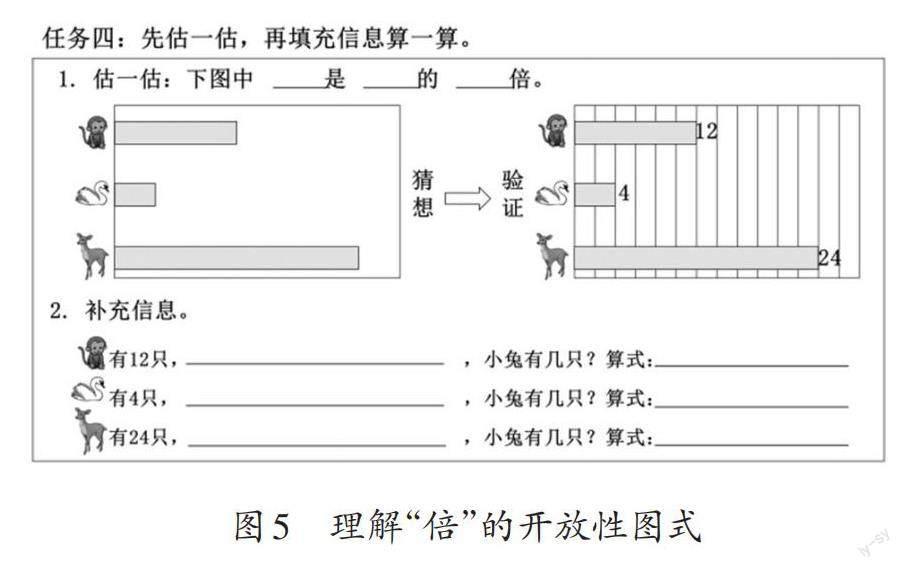
任务四是一组开放性的图式(如图5),学习材料从两个量的比较过渡到多个量的比较。教师出示任务四,旨在培养学生解决问题的综合能力。
首先,结合条形的长短猜想倍数关系体现了问题的开放。教师提问:“请你估一估,小猴、天鹅、小鹿的只数可能存在哪些倍数关系?”在此基础上呈现网格和具体数据,引导学生验证猜想,关注多个量的比较,判断标准量,用“谁是谁的几倍”进行描述。其次,条件和解题方法也具有开放性。教师可以引导学生思考:小兔也来凑热闹了,请在横线上补充跟小兔只数有关的信息,并列式计算小兔的只数。这样的学习任务充分激发了学生的学习兴趣,学生既有补充相差关系的,如“小兔比小猴多(少)2只”“小猴比小兔多(少)2只”等,也有补充倍数关系的,如“小兔的只数是天鹅只数的2倍”“小猴的只数是小兔只数的2倍”等。不同学生采用不同的数量关系和表述方式,补充的数据和解题的方法也有不同。他们在这些众多的表达中,发展了综合运用知识的能力。
学习的过程是知识不断同化和顺应的过程,而图式是同化和顺应过程中的重要工具。借助图式设置单元复习课的核心任务,有助于核心任务的整体呈现,契合学生的认知特征,能体现解题的过程化和思维的可视化,从而促进学生对概念的理解和认知结构的建构。
参考文献:
[1]方舒云.互助式单元复习课的教学实践与思考:以“倍的认识”单元复习教学为例[J].小学数学教育,2022(23):23-26.
[2]张优幼.以实证分析促进概念的深度理解:“有余数的除法”的教学重构[J].教学月刊·小学版(数学),2023(5):55-59.
[3]徐曙华.借图促思 深度学习:以“倍的认识”单元整理与复习课为例[J].教育界,2022(22):2-4.
(浙江省台州市学院路小学)

