巧解“方与圆”组合图形的面积
施志摩
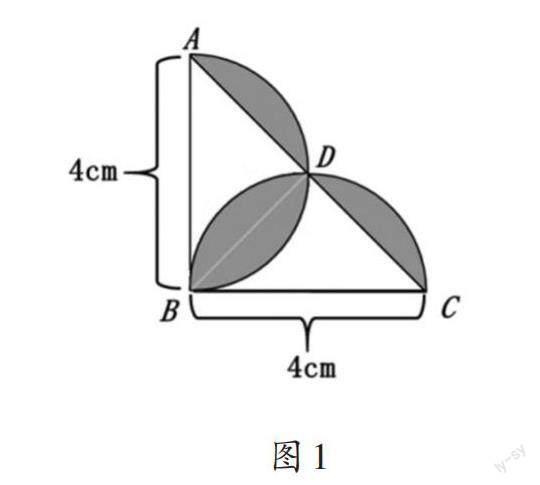
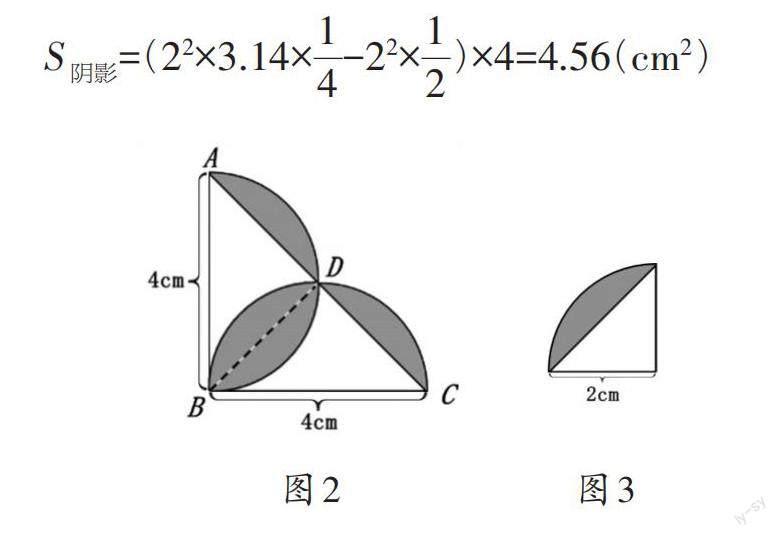
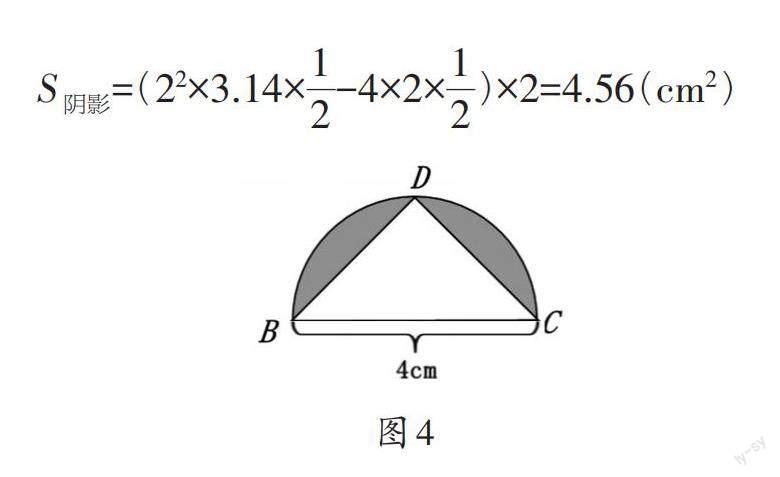
教材中的求“方与圆”组合图形的面积,是学生的一个学习难点。如何化难为易呢?可以采用以下教学过程。
一、尝试绘图,感知图形组合
1.看一看
教师出示图1,引导学生观察思考:这个组合图形是怎样绘制而成的?
2.画一画
让学生使用直尺和圆规绘制同样的组合图形(保留作图痕迹)。
3.说一说
学生绘制组合图形后,教师提问:“这个组合图形的阴影部分由哪几部分组成?分别是怎么构成的?”启发学生抓住组合图形的本质,用语言表达组合图形的结构。
二、解构重组,理解破题之法
1.算一算
讓学生独立计算图1中阴影部分的面积。
2.讲一讲
引导学生汇报:如何求阴影部分的面积?
预设1:连接BD(如图2),发现阴影部分的面积是由4个图3组成的。
预设2:连接BD,发现阴影部分的面积是由2个图4组成的。
预设3:连接BD,将左边(弧AB所在)的半圆绕点B顺时针旋转90度,把图1转化为外圆内方的形状(如图5)。
3.比一比
引导学生思考:以上几种方法有什么共同点?归纳得出:这三种方法都是通过连接BD,将阴影部分分割成4块相同的部分。
三、练习巩固,内化解题技法
1.选一选
练习1:下面哪几个图形阴影部分的面积与左图的阴影面积相等?( )
学生独立完成后,集体交流。
预设:因为图形①、图形②、图形③的阴影部分都能够分成与左图完全相同的4等份,所以这3个图形阴影部分的面积都与左图阴影部分的面积相等。此外也可以通过计算各个图形阴影部分的面积进行判断。
2.拓一拓
练习2:计算阴影部分的面积。
教师启发学生思考:怎样添加辅助线可以更快地求出阴影部分面积?然后组内交流,集体反馈。
上述教学借助尺规作图和图形的运动展开,既能帮助学生更好地理解求“方与圆”组合图形的面积的方法,又能培养学生的几何直观、推理意识,发展学生的空间观念。
(浙江省宁波市北仑区岷山学校)

