一致性视域下整数除法运算整体性的教学思考与设计
杨明岚

【摘 要】《义务教育数学课程标准(2022年版)》十分强调数与运算的一致性。教师以人教版教材三年级下册“除数是一位数的除法”单元为例,通过“提炼单元核心概念、构建单元教学序列”进行单元整体教学的思考与设计,凸显内容的整体性和原理的一致性,促使学生从知识系统化走向思维结构化。
【关键词】整数除法;单元整体;数与运算;一致性
《义务教育数学课程标准(2022年版)》十分强调数与运算的一致性,主要包括感悟数的概念本质上的一致性和体会数的运算本质上的一致性两个方面。在“数与代数”领域,要建立数的概念与数的运算之间的内在关联,通过数的意义理解数的运算,突出“数”与“运算”的一致性。
整数的除法运算是乘法运算的逆运算,除法运算的意义依附于乘法运算,其核心是计数单位个数的均分。那么,如何在整数除法运算教学中渗透运算的一致性呢?下面以人教版教材三年级下册“除数是一位数的除法”单元为例展开单元整体教学的研究。
一、教材内容分析
(一)除法运算
人教版教材分三个阶段编排除法运算:第一阶段“整数除法”,其实质是将被除数按不同计数单位进行分解,并利用分配律进行解构再细分;第二阶段“小数除法”,其实质是“披着小数外衣的整数除法运算”;第三阶段“分数除法”,目的是建立与整数除法的关系,贯通整数与分数的运算。
除法运算的一致性体现为计数单位与计数单位相除,计数单位的个数与计数单位的个数相除。将“除数是一位数的除法”教学单元置于“除法运算”的结构中进行整体考量,凸显了内容的整体性、原理的一致性及目标的进阶性。
(二)整数除法运算
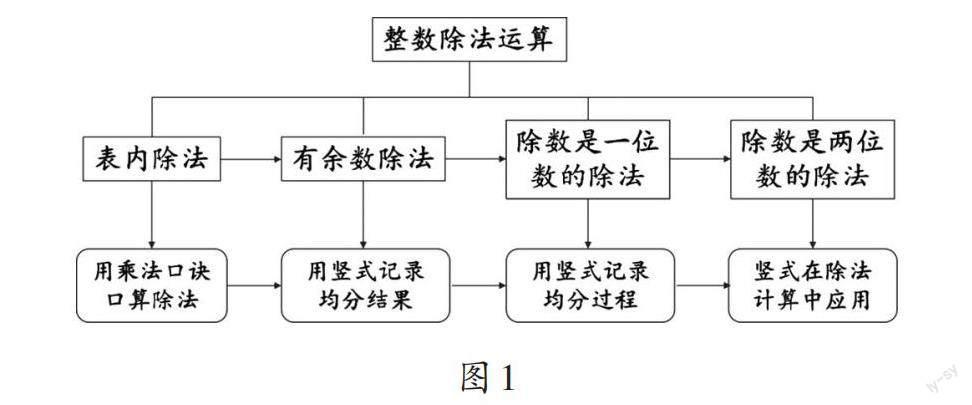
对于整数除法运算,人教版教材依次编排了“表内除法”“有余数的除法”“除数是一位数的除法”“除数是两位数的除法”等内容。在二年级下册“表内除法(一)”和“表内除法(二)”单元,学生第一次接触除法,理解除法的含义,认识除法是乘法的逆运算;在“有余数的除法”单元,学生第一次接触除法竖式;到三年级下册“除数是一位数的除法”单元,学生开始理解除法竖式的算理与算法;最后,在四年级上册“除数是两位数的除法”单元,除数由一位数扩展至多位数。整个“整数除法运算”(如图1)通过横向打通知识脉络,与学生的认知结构建立联系。
(三)除数是一位数的除法
“除数是一位数的除法”是“整数除法运算”中的关键单元,具有承上启下的作用。本单元按照“口算除法—笔算除法—用估算解决问题”的顺序编排教学内容。这样的编排序列在实际教学中有一定的合理性,但结合学生的学习起点来分析,有两个问题值得探讨:一个是口算除法中编排的例题难度较小、梯度过缓,导致多数学生只关注除的“结果”,而忽视除的“理”和“过程”。从算理与算法间的关系看,口算除法的算法是笔算除法的算理。另一个是知识板块缺少衔接,不利于内容的整体关联。首先,口算除法与表内除法关联不够。教学口算除法应与表内除法均分的过程密切联系,如针对教材提供的素材“10张一沓的彩纸”,就需要让学生经历“为什么选择6个十均分,而不选择60个一均分”的深度思考。其次,笔算除法与口算除法关联不够,学生不理解“有口算方法了为何还要学竖式方法”。
二、学情分析
在遵循学科逻辑的基础上,教学时还要遵循学生的认知起点。为精准把握“除数是一位数的除法”单元中学生的认知起点,了解学生学习的真实疑难点,笔者在教学前组织了一次单元知识的前测,随机抽取80名学生进行测试,具体情况如下。
测试题目1:口算120÷3=、66÷3=,用自己的方法清楚地表示计算的过程。
测试结果显示,两道口算题学生的正确率达97.5%。部分学生用横式来表示计算过程,如“120÷3”,因为12÷3=4,所以120÷3=40;又如“66÷3”,因为60÷3=20,6÷3=2,所以20+2=22。部分学生用圆圈图(120个圆圈)、小棒图(120根小棒)圈出结果。少部分学生用12捆小棒圈出均分的结果。
测试题目2:笔算69÷3=、72÷3=、327÷3=,用列竖式的方法表示计算的过程。
测试结果显示:只有约12.5%的学生能正确运用除法竖式进行计算,通过访谈得知,他们是通过看书、父母告知等途径习得计算方法的;约18.8%的学生是将加、减、乘的竖式书写(从上往下写)经验迁移至了除法竖式;约46.3%的学生用一层的除法竖式书写。分析测试结果可知,多数学生不会用多层竖式书写,不理解除法竖式中每一步的含义。
前测结果表明,学生口算的正确率非常高。从技能层面看,学生能自主迁移运用乘法口诀进行计算,熟练掌握运算的技能;从理解层面看,有少部分学生能解释这样运算的道理,但多数学生只关注除的“結果”,而忽视除的“理”。基于上述分析,学生学习本单元内容时存在三方面的难点:一是理解口算除法时,对把被除数按计数单位分解成若干个部分(如66可以看作6个十和6个一),再均分每部分单位的个数(如先分6个十,平均分成3份,每份是2个十;再分6个一,平均分成3份,每份是2个一)的理解存在障碍;二是对除法竖式的价值理解、算理理解和竖式的含义无法同步匹配,即在理解除法竖式每一个数的含义、每一层均分的含义上存在困难;三是在除法竖式中,随着被除数的增大,商的位数增多(出现商中间有0的情况),学生在运用多层记录的方式进行计算时遇到了挑战。因此,教师需要进一步思考两个问题:一是如何迁移数的意义,深度理解除法的意义;二是如何获得算理的支持,理解除法竖式每一步的含义。
三、单元教学框架重构
(一)单元核心概念提炼
核心概念指向数学学科结构的主干部分,能反映学科对象本质关联的内容。本单元内容由“数的意义”引申出“数的结构”,即“数+计数单位”。其中,“计数单位”是数的构成的核心。据此,本单元的核心概念可提炼为“均分计数单位的个数”,也就是对计数单位个数的运算。在此基础上,确立“除数是一位数的除法”的单元目标:(1)通过数的意义的迁移,自主探索“除数是一位数的除法”的算法和算理,并能灵活选择合适的算法解决实际问题;(2)在探索一位数除多位数的方法及估算方法的过程中,提高运算能力和推理意识,积累数学思考的经验。
(二)单元核心内容重构
基于以上分析,笔者对“除数是一位数的除法”单元的教学内容作了适度的调整(如表1)。
重构后的教学内容主要有如下变化。
1.联系数的意义,理解除法运算的原理
从运算的意义看,数的运算源自数的意义,即对计数单位个数的运算。因此,笔者将“均分计数单位个数”确立为单元核心概念,以此串联本单元的课时学习。重构后的理解算理课是本单元的关键板块,笔者有机整合“口算除法”的3个例题,设计“分一分1(每一位都能均分)”“分一分2(某一位不能均分)”两个学习进阶活动,让学生借助“分小棒”的过程,在求同寻异中理解被除数按计数单位进行“拆—除—合”的运算过程,体会快捷计数的价值。
2.关联计数原理,迁移笔算除法的技能
从运算的一致性看,加、减、乘、除运算都是“数”计数单位个数的运算。本单元的“笔算除法”是形成算法的关键板块,笔者尝试联系“口算除法”中“分小棒”的过程,设计“除法竖式”的三个学习进阶活动,将“分小棒”的过程与除法竖式分层记录的过程结合起来,帮助学生理解竖式的含义;同时建立“加法、减法、乘法、除法”竖式之间的联系,让学生理解竖式是记录计数单位个数的运算,感悟运算原理的一致性,实现教学内容的结构化,促进学生思维的结构化发展。
四、单元教学课堂实践
基于上述分析,笔者围绕单元重构后的3个关键课例进行例证。
【课例1】分一分1(每一位都能除尽)
1.回顾旧知,理解意义
教师直接出示题目:口算6÷3=、69÷3=。
问题1:6个一平均分成3份,均分了几次?
问题2:按照6÷3的分法,69个一平均分成3份,需要均分几次?
2.画图表征,理解算理
教师布置学习任务:有没有一种简便的分法能让69÷3分的次数最少,可以画一画、写一写。
对比分析:这些作品(如图2)中有什么相同的地方?
3.关联方法,迁移技能
教师出示题目:口算369÷3=、6369÷3=。
问题1:这两道题目分别需要均分几次?
问题2:均分的道理和69÷3一样吗?如果是五位数、六位数呢?
【课例2】分一分2(某一位不能除尽)
核心环节教学:对比沟通,理解算理的一致性。
教師布置学习任务:分一分,圈一圈,清楚地表示两次分的过程。
42÷3= 43÷3= 24÷3=
全班交流反馈:均分的过程中遇到了什么新问题?你们是怎么解决的?
师:你们是怎样均分的?
生:42÷3是将十位的4个十平均分成3份,每份分到1个十,还剩1个十,再把1个十拆成10个一,与个位的“2个一”合起来再分(如图3)。
生:43÷3的分法和42÷3的分法基本一样,不一样的是43÷3分到最后个位还有余数1(如图4)。
师:是的,个位有余数。那如果还要继续均分,怎么办?
生:把个位的余数“1”变成更小的计数单位后再分。
生:均分24÷3时,十位的“2个十”不够平均分成3份,所以要把2个十变成20个一,和个位的4个一合成24个一后再分。
小结:被除数是几位数就均分几次,不够分的时候,先将大的计数单位细分成小的计数单位再继续均分,除法就是将计数单位细分再不断均分的过程。
【课例3】除法竖式1(被除数是两位数)
1.数形结合,理解竖式
教师布置学习任务:用竖式记录69÷3两次均分小棒的过程和结果。
教师用课件演示两次均分小棒的过程(如图5)。
对比学生用竖式记录的多种方法(如图6)。
问题1:哪一个竖式把刚才两次均分小棒的过程毫无遗漏地记录下来了?
问题2:结合口算除法中两次分小棒的过程,哪个竖式能显示两次均分小棒的过程?
问题3:②号竖式和③号竖式有什么相同点和不同点?
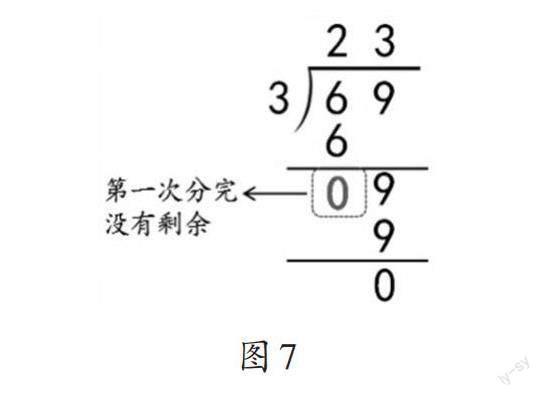
小结:第一次分完6捆小棒后没有剩余,可记为“0”(如图7),这样就能毫无遗漏地把两次均分的过程都记录下来。
2.思维关联,深化算理
教师布置学习任务:用竖式计算42÷3=、43÷3=、24÷3=。
问题1:你能在竖式中找到两次均分的过程吗?
问题2:第一次均分的过程中遇到了什么问题?你是怎么解决的?
3.内容关联,关注一致
教师布置学习任务:用竖式计算69÷30。
问题:你能在竖式中找到每次均分的过程吗?
“除数是一位数的除法”单元是整数除法的关键单元。教学时,可以“均分计数单位的个数”这一核心概念统摄整个学习过程,通过3个例证内容渗透运算的一致性,让学生理解“除数是一位数的除法”的算理与算法,向前联系“表内除法”的均分经验,向后连接“除数是两位数的除法”“小数除法”,将本单元置于整体教学中,凸显知识原理的一致性。
参考文献:
[1]巩子坤,刘萍.论数的概念与运算的一致性之三:整数运算算理、算法的一致性[J].小学数学教师,2022(10):77-81.
[2]叶婉贞.单元整合 疏通联系 发展学力:“除数是一位数的除法”单元整合探索[J].小学数学教师,2020(9):69-73.
[3]史宁中.基本概念与运算法则:小学数学教学中的核心问题[M].北京:高等教育出版社,2013.
(浙江省湖州市长兴县教育研究中心)

