初中数学圆中最值问题解题技巧的探究
林 越
(无锡市积余实验学校,江苏 无锡 214043)
圆是数学中一个重要的几何图形,在实际生活和数学理论中都具有广泛的应用.与圆有关的最值问题作为初中数学的一部分,是培养学生解决实际问题和培养数学思维的关键内容之一.然而,由于其涉及圆的特殊性质,求解过程较为复杂,许多学生在解题过程中常常感到困惑和迷茫,因此,教师研究圆中最值问题的解题技巧,对于提高学生的数学能力和解决实际问题具有重要意义[1].
1 紧扣概念,垂线段求最值
在初中数学中,圆的垂线段是指从圆上的一个点向圆的直径或半径所引的线段.这条线段与所引的直径或半径垂直相交,被称为垂线段,在圆的解题中,垂径是一个特殊的位置,对圆的最值问题可以造成一定的影响,因此,教师在课堂中可以引入垂线段求圆的最值的技巧.
垂线段的特点是它的两个端点分别位于圆上和圆心上,并且与圆的直径或半径垂直相交.在课堂上,教师可以带领学生研读教材,紧扣概念,理解圆的特殊位置.通过紧扣概念求解圆中垂线段的最值,教师可以通过提供一些实际问题,引发学生的思考和讨论.例如,给定一个圆,学生可以思考如何找到圆中垂线段的最大值或最小值,或者如何确定垂线段的长度在什么条件下取得最值.教师可以指导学生从几何角度出发,利用相似三角形或勾股定理等数学工具进行推理和证明.学生思考完如何找到圆中垂线段的最大值或最小值后,教师可以引导他们从几何角度出发,利用相似三角形和勾股定理等数学工具进行推理和证明.首先,教师可以考虑如何找到圆中垂线段的最大值,可以假设圆的半径为r,垂线段的长度为x,然后通过相似三角形来解决这个问题,教师可以在圆上选择一个点A,连接圆心O和点A,并假设点B为垂线段的另一端点.根据相似三角形的性质,可以得到比例关系x:r=r:(r+x),从而可以得到一个关于x的一元二次方程x2-rx-r2=0,解这个方程,便得到两个解.根据实际意义,垂线段的长度必须为正值,因此需要取正解.接下来,教师可以带领学生考虑如何确定垂线段的长度在什么条件下取得最小值.在了解基本概念后,教师可以带领学生实战演练.
例1如图1,在圆O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC,且与圆O相交于点D,则CD的最大值为多少?
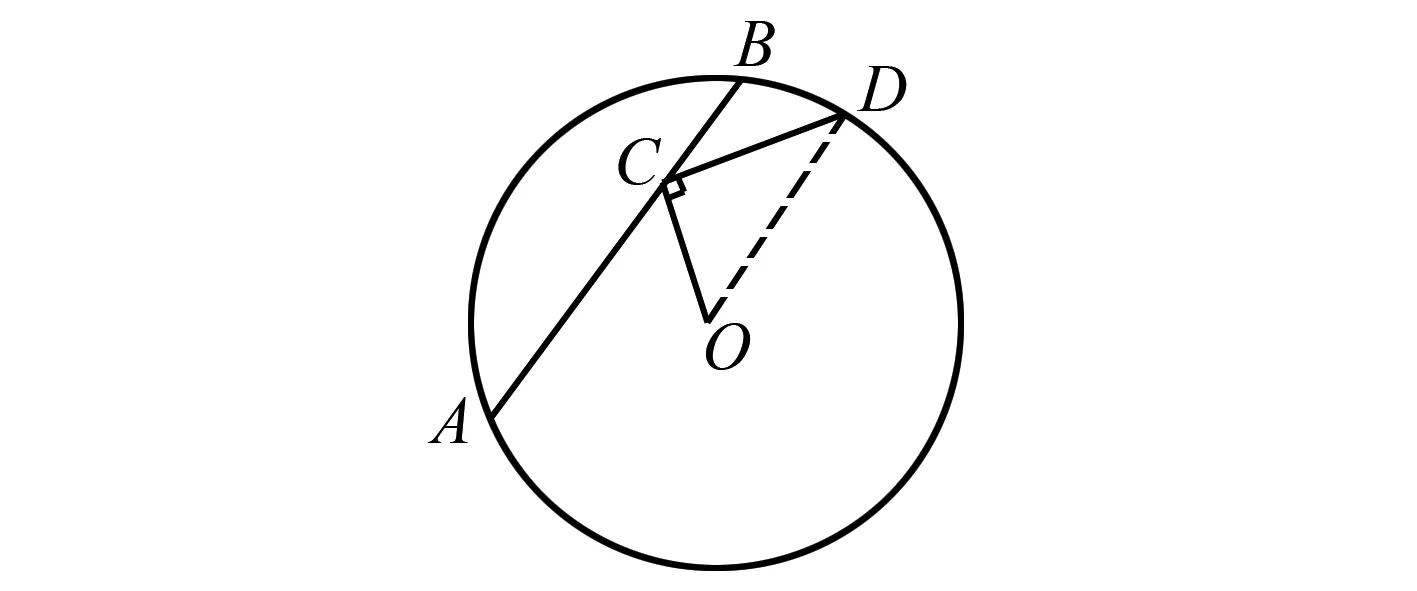
图1 圆作垂线段的示意图

通过这样的教学方法,学生不仅可以掌握解决圆中垂线段最值问题的方法,还能培养学生几何图形的空间感,让学生在图形的动态与静态的转化中找到临界点,帮助学生提高对数学圆图形的全面认识,找到解题的多重技巧,并突破数学学习瓶颈,找到数学学习的自信心.
2 位置转化,对称点求最值
对称点是指平面上的两个点,它们相对于某个中心点或某条直线对称,即以这个中心点为对称中心或以这条直线为对称轴,两个点的位置互相镜像,对称点在平面几何中起到重要作用,常常用于解决对称性相关的问题.圆图形本身属于对称图形,因此,教师可以在课堂中为学生渗透丰富的对称知识,帮助学生学习转化特殊点、特殊线段的位置,从而求解最值[2].
对称方法在圆中求最值可以帮助学生降低计算的难度,由于圆具有旋转对称性,其任意一点的性质都与其对称点相同,因此,在使用对称方法时,只需计算部分圆内的点,然后通过对称性推断出其它对应点的值,而无需逐个计算所有点.通过利用对称性,教师可以将问题简化为只需考虑部分圆内的点,从而减少了可能出错的计算步骤,这样一来,学生能够更加准确地求得圆中的最值,避免了由于繁琐的计算过程导致的误差累积.此外,通过观察和利用圆的对称性,学生还可以更加直观地理解问题,并通过图形化表示来帮助自己解决问题,从而更加清晰地把握问题的本质,更好地求得圆中的最值.教师可以带领学生探索例题解法,促进学生领悟对称求最值的奥秘.
例2 如图2,AB是圆O的直径,点M在圆O上,且AB=8,∠MAB=20°.N点是弧MB的中点,P是直径AB上的一个动点,如果MN=1,则△MNP周长的最小值为多少?

图2 圆中作对称的示意图
教师可以在图形中作出辅助线,如图2所示.作N关于AB的对称点N′,连接MN′,NN′,ON′和ON.根据图形可以看出,MN′与AB的交点P′即为△PMN周长的最小时的点,并且又因为N是弧AB的中点,此时有学生回答,这一步得出了∠A=∠NOB=∠MON=20°,也就进一步推出了∠MON′=60°,所以根据等边三角形的特点,可以推论出周长的最小值为5.
利用作对称的方法求最值,有利于降低计算过程的复杂性,提高学生的计算效率,减少出错可能性,增强问题的可视化.同时,这种方法还能够简化问题,形成简单的模型,帮助学生提高解决问题的效率和准确性,让学生更好地应用数学原理和工具解决实际问题,培养学生的核心素养.
3 技巧升格,阿氏圆求最值
阿氏圆是一个由希腊数学家阿波罗尼乌斯在数学中引入的概念,它是由三个互相切于一点的圆构成的,这些圆可以是内切或外切的,这些圆的切点和切线之间存在一些特定的关系.教师可以在数学课堂中为学生引入阿氏圆的概念,帮助学生求解隐圆的最值难题.
在初中数学中,学生通常会在几何学的学习中接触到阿氏圆,学生需要学习如何构造阿氏圆、确定它们的性质以及探索它们的几何关系.首先,教师可以带领学生了解阿氏圆的定义,教师需要让学生了解阿氏圆是由三个互相切于一点的圆构成的,并且这些圆可以是内切或外切的,然后带着学生探索阿氏圆的性质,学生可以通过构造阿氏圆,观察它们的性质.为了更深入地理解与阿氏圆相关的问题,教师可以带领学生尝试解决一些与阿氏圆相关的问题,如给定一些切点和切线的条件,求解阿氏圆的半径和圆心的坐标等,帮助学生逐渐认识和理解阿氏圆,并掌握与之相关的概念和技巧.
例3如图3,圆O的半径为r,点A和点B都在圆O外,点P为圆O上的动点,已知r=k·AO,连接PB与PA,则当PB+k·PA的值最小时,P点的位置如何确定?

图3 阿氏圆的示意图
经过前期的教学铺垫,教师可以让学生分析题意,有学生指出两条线段的最值问题可以转化成两点之间的线段来解决,如图3所示.本题的关键在于如何确定待定系数k与AP乘积的大小.此时,另一位学生指出,可以根据题目中给出的条件得到关系式PB+k·PA,然后可以将PA表示为PO+OA,其中PO为圆心O到点P的距离,OA为点A到圆心O的距离.因此PB+k·PA=PB+k(PO+OA),PA是圆O上的动点,所以PA的长度是固定的,即PA=2r.将其代入上式得PB+k·PA=PB+k(PO+2r).接下来,需要分析PB和PO之间的关系.由于点B在圆O外,所以PB的长度是固定的,即PB=2r.将其代入上式得PB+k·PA=2r+k(PO+2r).再确定k的值,使得PB+k·PA的值最小,就可以将上式化简为2r+k(PO+2r)=2r+k·PO+2kr,由题意可以发现,PO是圆心O到点P的距离,而我们知道,圆心O到圆上的任意一点的距离是固定的,即PO=r.将其代入上式得2r+k·r+2k·r=(2+k+2k)·r,然后只需要确定k的值,使得(2+k+2k)·r的值最小.由于r是圆O的半径,是固定的,所以只需要确定k的值即可,为了使(2+k+2k)·r的值最小,我们需要使k的值尽可能小.由于k是待定系数,可以取任意实数,所以我们可以取k=0这样,(2+k+2k)·r的值就达到了最小值.因此,当k=0时,P点的位置可以确定为圆O上与点A相对的点.
通过阿氏圆求最值的方法,学生可以更好地理解圆的概念,让圆的概念突破传统的题目设定的框架,阿氏圆的概念将几何图形与代数式结合了起来,有利于学生找到两者中的平衡关系,提升思维品质,从而更好地求解圆中最值问题[3].
综上所述,学生学习圆的最值问题具有重要性和意义,圆的最值问题涉及如何通过数学方法确定圆的最大值或最小值,如何通过建立数学模型、推理和计算,找到最优解.这种思维方式可以培养学生的逻辑思维、数学思维和问题解决的能力.学生掌握了圆的最值问题,不仅可以培养分析和解决问题的能力,还能够发展数学建模和抽象推广的能力,为学生的学习和未来的发展打下坚实的数学基础.

