思维导图在初中数学教学中的应用
曹育胜
(江苏省灌南县淮河路实验学校,江苏 连云港 222500)
数学的抽象性和逻辑性都很强,因此,在数学学习中,学生需要具备一定的逻辑思维能力和建构思维能力.在初中数学教学中,教师可利用思维导图培养学生的逻辑思维能力和建构思维能力,提升初中数学教学效果.
1 思维导图的内涵和应用价值
思维导图是一种结构化的思考工具,它是充分运用一系列图片、形状、色彩、逻辑符号和关键词等要素,构建的一套模拟人脑思考过程的思维方法.它借助图形、色彩等要素实现了抽象的数学思维可视化,将数学思维转化为直观、形象、有条理、有层次的演示图形,从一种提高初中学生记忆力的笔记方式发展成为一种激发创造性思维的思考方式.由此可以看出,思维导图能够帮助教师厘清教学思路,构建更加有序、全面的数学知识体系.思维导图运用在初中数学教学实践中的价值主要表现在两方面.
一方面,思维导图设计过程可以为初中学生创造一个数学知识的应用场景.它从条理性和层次性的维度上降低了学生自主思考的难度,有助于吸引、刺激学生自主学习数学的兴趣,提高学生独立思考的能动性和自信心.上述过程不仅可以培养学生自主进行课前预习的能动性及建构思维能力的创造性,还有利于培养学生在课堂教学中有侧重地理解相关的困惑或难点,更有助于学生在课后复习时回顾、盘点相关知识点,巩固和提升复习效果[1].
另一方面,思维导图的设计结果可以让初中数学教师了解学生的学习基础和认知水平,挖掘一些共性的难点和困惑,有利于教师在课堂教学时有针对性、有侧重点地讲解相关的知识难点或者容易混淆的概念.上述过程不仅提高了初中数学教师的教学效率和效果,也提升了初中学生的学习效率和效果,充分发挥了教学相长的优势[2].
2 初中数学教学运用思维导图的实践
本文以苏科版初中数学七年级上册第二章《有理数》为例,设计培养学生运用思维导图能力的教学方案,旨在强化思维导图在初中数学教学的实践运用,训练学生的逻辑思维能力和建构思维能力.
2.1 初中数学课前预习的优势和问题
初中数学教师通常都会让学生进行课前预习.初中数学课前预习有什么优势呢?课前预习不仅可以让学生提前梳理本节课的重点、难点,还可以让学生提前找出预习时发现的不理解或者容易混淆的定义、原理或公式推导过程的困惑等,更可以让学生在课堂教学时有侧重点地理解预习时遇到的困惑或难点,从而提高学生的学习效率和效果.课前预习不仅有助于初中数学教师在课前导入时摸清学生的认知水平和学习基础,掌握学生在预习过程中的一些共性的认知难点或者容易混淆的易错点,还有利于教师实时掌握教学重点和难点,有针对性地调整教学思路和计划,开展高效、务实的课堂教学.
然而,在教学实践中发现很多学生虽然提前预习了课程,但是课前预习的效果不是十分理想.课前预习不理想的主要问题集中表现在如下两个方面.一方面,学生在没有教师指导的情况下还不能较全面地梳理出所预习内容的逻辑框架,例如主次不分、逻辑不清或者错误等;另一方面,在课堂教学时,学生不是专心听讲,而是忙着记笔记、抄板书,呈现出一种被动式的、疲态的学习状态,甚至影响了听课节奏,降低了教学效果.
2.2 初中数学课前预习运用思维导图的实践
初中学生应当如何正确地开展数学课前预习呢?教师可引入思维导图法,指导学生按照基于思维导图的预习方法进行课前预习.例如,在学习“有理数与无理数”时,教师可引导学生将有理数和无理数的定义、分类等教学内容按照思维导图的教学方法,全面有序地引导学生进行课前预习.为了培养初中学生按照思维导图设计进行课前预习的自主意识,降低学生学习的难度,教师可将全班30名学生划分为6组学习小组,让每个学习小组的5名同学推选出可以协调和组织自己小组同学的组长.然后,每组小组长根据各组学生的特点进行分工,组织和协调各个组员进行课前预习,并设计思维导图.例如,小组组长负责统筹课前预习的思维导图设计的分工、合稿、复核和成果汇报等;2名小组同学合作,对有理数的概念、性质和推理等知识点进行逻辑梳理和关键词提炼,并整理、汇总和呈现出文字版的知识结构;另2名小组同学合作将文字版的知识结构进行可视化,设计成为图文并茂、逻辑清晰、层次分明的思维导图.由此,通过学生之间分工与合作,达到优势互补.在自主预习中,每组学生取长补短,群策群力,在合作预习中,提高了呈现预习成果的效率和效果,实现了共同成长,共同进步,共同提高.
2.3 初中数学课堂教学运用思维导图的实践
在课堂教学前,教师先让6个学习小组的代表分别来讲解各自小组按照思维导图方法得到的课前预习结果.在每个小组的代表讲解预习结果过程中,承担讲解的学生代表汇报了所在小组的预习成果,也一定程度上暴露了所在小组的学生在预习过程中存在的问题和不足.由此,教师间接了解了每组学生的学习基础和认知水平,结合上述学生呈现的学习基础和认知水平及发现存在的一些共性的难点和困惑,在课堂教学时,教师会有针对性地、有侧重点地讲解相关的知识难点或者容易混淆的定义等.
[有理数和无理数的定义区分]
如何区分有理数和无理数呢?定义是区分上述两种类型的数的关键.根据有理数和无理数的定义,可以将“能否转化为分数”作为衡量标准,用来区分有理数和无理数.
例如,π约等于3.141 592 6…,属于无限不循环的小数,无法转化为分数,因此π是无理数.再例如0.5可以转化为分数,它是有理数.还如-0.6也可以转化为分数,它也是有理数.
[有理数和无理数的逻辑分类]
正数、负数和0,以及自然数和分数等,上述类型的数是按照什么标准分类的呢?分类之后它们之间存在什么逻辑关系呢?不同的分类标准下是否会出现不同的分类呢?
一是将“是否可以转化为分数”作为衡量标准对数进行分类.在这种分类标准下,有理数和无理数是并列的不同类型的数,“可以转化为分数的数”为有理数,否则为无理数.分数属于有理数,整数可以看作是分子是整数本身、分母为1的分数,也归为有理数.那么,有理数涵盖了整数和分数.
二是将“数的正、负号”作为衡量标准对数进行分类.在这种分类标准下,有理数和无理数是并列的不同类型的数,有理数可以分为正有理数、0和负有理数.无理数可以分为正无理数和负无理数.
[有理数和无理数的思维导图]
在按照不同标准对有理数和无理数进行逻辑分类后,教师可按照不同衡量标准全面、有序地引导学生构建有理数和无理数的思维导图.
图1是按照定义对有理数和无理数进行分类的思维导图,从图1可以看出,思维导图全面地展示了有理数和无理数定义的区分重点及相互之间的分类、逻辑关系等.
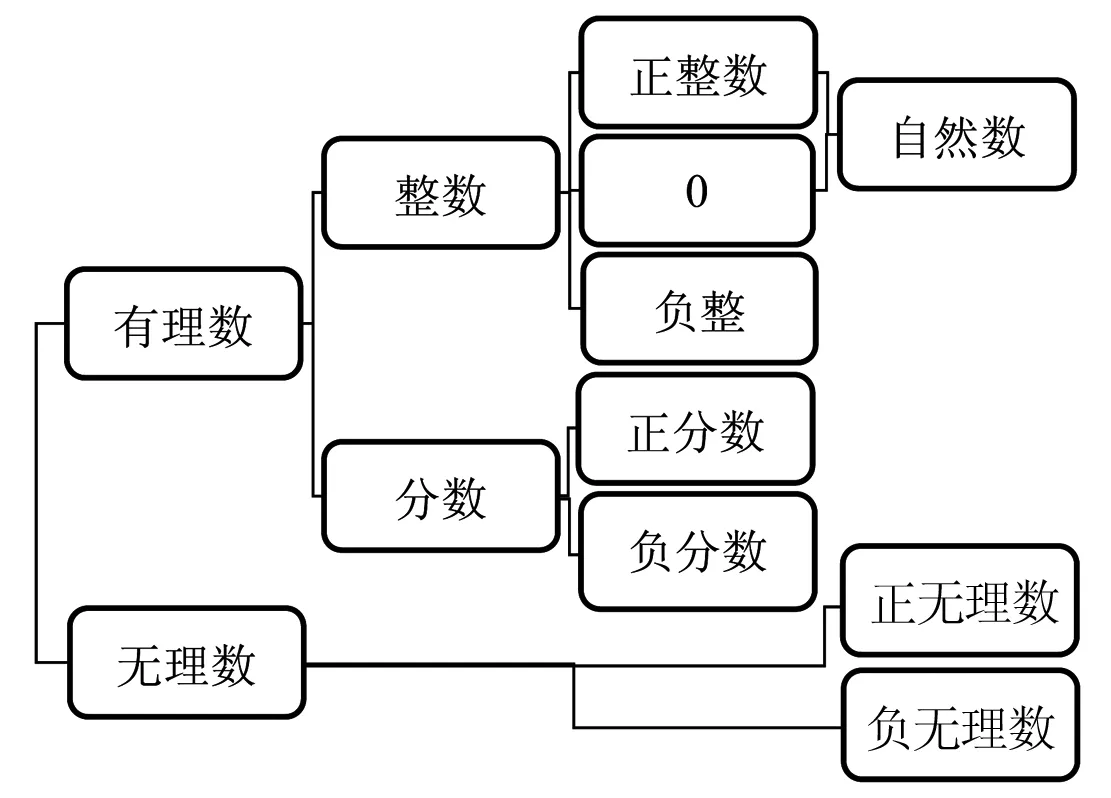
图1 有理数和无理数分类图
图2是按照“数的正、负号”对有理数和无理数进行分类的思维导图.从图2可以看出,思维导图可以全面地展示有理数和无理数的分类、逻辑关系及定义的区分重点.

图2 有理数和无理数分类图
上述思维导图设计成果的展示和教学,有助于初中学生在课堂教学中有侧重地理解困惑或难点,及时对自己设计的思维导图进行查漏补缺,然后进一步完善和优化.这种按照思维导图进行课前预习的学习实践活动,可以更快地提升学生设计思维导图的质量和效率.
2.4 初中数学课后复习运用思维导图的实践
在课前预习时,初中学生借助思维导图的设计梳理了有理数和无理数的相关定义及分类等,厘清了难点和容易混淆的知识点.在课堂教学时,学生也及时查漏补缺了课前设计的思维导图,有侧重地学习了相关的知识难点和重点.在课后复习时,学生经过不断地完善、优化各自所设计的思维导图,有助于学生全面、准确地回顾相关的知识框架、内在逻辑,理解和运用所学知识解答相关问题,从而更进一步巩固和提升了复习效果.
由此可以看出,思维导图设计方法在初中数学教学中具有重要作用.一是初中数学课前预习思维导图的设计不仅提高了初中学生独立的思考能力,还创造性地培养了学生的构建思维等逻辑能力;二是在初中数学课堂教学前每个学习小组代表展示课前预习思维导图设计结果,有助于教师发现学生在课前预习中存在的共性问题,评估学生目前的学习基础和认知水平;三是在初中数学课堂教学中,教师结合课前预习思维导图的设计结果,可以有针对性、有侧重点地讲解相关的知识难点或者容易混淆的定义等.学生结合课前预习思维导图的设计结果可以在听讲时进行思维导图的查漏补缺,充分发挥教学相长的优势;四是在初中数学课后复习时,完善思维导图的设计成果,有助于学生全面、准确地回顾相关的知识框架,理解和运用相关的知识来解答相关的题目,也有利于学生巩固和提升复习效果.总之,在初中数学教学中,思维导图的运用实践不仅培养了学生的逻辑思维能力和建构思维能力,还提升了学生的数学核心素养和教师的教学效果.

