基于运算本质一致性的结构化教学探索——《分数四则混合运算》教学

文|李柱俊

【教学内容】

苏教版六年级上册第75 页例1 和“练一练”，第76 页的第1～5 题。

【教学过程】

一、自觉提问，尝试计算

师：同学们，看到课题，你们想问什么？

生：什么是分数四则混合运算？（板书：是什么？）

生：分数四则混合运算怎么算？（板书：怎么算？）

生：它和整数、小数四则混合运算有联系吗？（板书：联系？）

师：会提问也一定爱思考，我们首先看看第一个问题：什么是分数四则混合运算？谁可以举例说明？

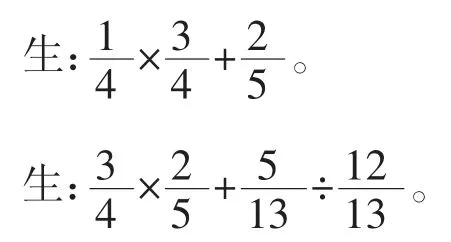
（教师巡视，收集按运算顺序做和运用乘法分配律简便计算的两种不同作品）

【设计意图：结合学生的学习心向，开门见山让学生根据课题提出问题，培养学生问题建构力的同时，也激发了学生学习的热情。】

二、自主研究，理解算理

1.多元计算，理法相融。

（1）小组探究

师：我们先来看看这位同学的计算（如下图），他是按怎样的顺序计算的？

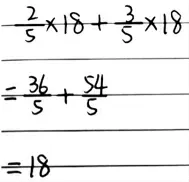
师：你们的得数和他一样吗？

师：先算乘法，再算加法，到底合不合理？（板书：运算顺序合理？）

师：数学是讲道理的学科，你能想办法证明吗？以小组为单位，每个小组至少选择两种验证方法。有困难的可以看看研究小贴士。

【设计意图：运算顺序的合理性是分数四则混合运算的核心要素之一，从问题出发，逆向而行，引领学生探究算法和算理之间的关系，指向的是在学习过程中运算能力这一核心素养的落实。】

（2）算理交流

●方法一：转化成小数

师：这是谁的研究成果？（如下图）说说你是怎样想的。

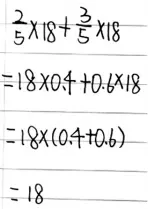
小结：将分数改写成了小数，得到相同的结果，证明了先算乘法的合理性。（板书：分数、小数）

●方法二：编题法

师：（如下图）这是通过编题来证明的，你能根据他编的题目说说为什么可以先算乘法吗？

小结：借助解题思路分析了先算乘法的合理性。

●方法三：把分数量转化成整数量

师：你能看懂这幅作品的想法吗？（如下图）

生：他是把分数表示的量用整数来表示，再进行计算的。（板书：整数）

●方法四：画图法

师：能看懂别人的做法是会学习的表现。这还有一位同学是画图解释的。（如下图）

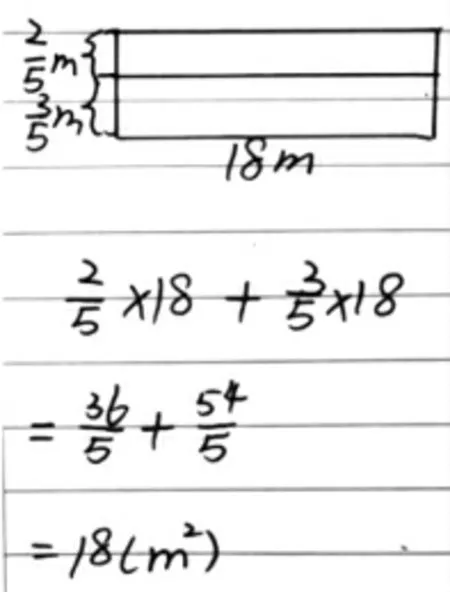
师：从他的图中你明白了为什么可以先算乘法吗？

2.引导比较，归纳算法。

师：观察几种不同的验证方法，都证明了什么？

师：看来按照这样的顺序计算是合理的（擦去合理后面的问号），这个运算顺序我们熟悉吗？

生：其实就和整数、小数的混合运算顺序是一样的。

小结：分数四则混合运算的运算顺序和整数、小数四则混合运算的运算顺序都是一样的。（板书：运算顺序一致）

【设计意图：运算顺序的一致性是分数四则混合运算的另一个核心要素，在对运算顺序合理性的询证过程中，学生感悟到其实分数四则混合运算的运算顺序是与整数、小数的混合运算顺序一致的。】

三、联通算理，优化算法

师：老师巡视的过程中，发现有同学是这样做的（如下图），猜一猜，他是怎么想的？

生：他运用乘法分配律进行了简便计算。

师：乘法分配律在分数混合运算中适不适用？你能不能结合编的题目解释算的是什么？

师：还有不同的吗？

师：谁还能结合这幅图来说说？

师：这几位同学结合解题思路都说清楚了先算括号里的加法也是合理的。是在做同一件事情，它们之间是相等的关系。18 可以变化成证明了什么？

生：乘法分配律也可以用在分数中。

师：原来，整数的运算律对于分数同样适用。（板书：运算律适用）如果是你，你会选择哪一种来计算？为什么？

生：第二种，因为更简便。

师：是的，在这里数字就是这么巧合，有时运用运算律可以使计算更简便。（板书：简便）

回顾：回头看看大家之前提出的问题，你现在知道怎样计算分数四则混合运算吗？

追问：分数、小数、整数四则混合运算之间有什么联系？

小结：分数、小数、整数四则混合运算的运算顺序都是一致的，运算律也适用于分数四则混合运算。

提问：课的开始同学们列举的两道分数四则混合运算，说一说分别是按照什么运算顺序计算的。

【设计意图：让学生对自己和他人的问题解决过程给出合理解释，提供不完全归纳发现运算律对于分数四则混合运算也同样适用，有助于学生养成讲道理、有条理的思维习惯，发展学生的推理意识和能力。】

四、巩固练习，强化规则

1.能简算的要简算。

（1）独立完成。

（2）核对、反馈。

（3）追问：明明是先算除法的，为什么转化成乘倒数后就一起算了呢？

（4）强调：在计算分数四则混合运算时，有时要边算边看能不能简便。

2. 在下面各数中间添上运算符号或括号，并计算出得数。

（1）说说你是怎么想的。

（2）追问：几道算式四个数都相同，为什么结果不同？

3.在下面各数中间添上运算符号或括号，使等式成立。

【设计意图：结合运算能力和推理意识的能力素养表现，基于分数四则混合运算的两大核心要素，设计了三道整体性、进阶性的习题，习题1 是基础题，习题2 是标准题，习题3 是挑战题。潜能生可不做挑战题，优等生可不做基础题，所有学生都要做标准题。】