抓住关键点渗透模型意识

文|孙保华（特级教师）

数学模型是根据特定的研究目的，采用形式化的数学语言，表征研究对象的主要特征和数量关系所形成的一种数学结构。小学数学课程中的数概念、关系、运算、图形、数据等都直接源于现实生活，是对现实模型数学化的结果，而当这些数学对象被用于解决现实世界的问题时，又需要借助具体的模型表达实际意义。通过建立这种数学与现实世界的双向联系，学生可以形成初步的模型意识。考虑到小学生年龄特征和认知能力，模型意识的发展应以渗透的方式为主。如何来渗透模型意识呢？笔者结合自己的教学实践，归纳总结了以下几个渗透的关键点。

一、联想拓展——一般性

数学模型是解决一类问题的基本数量关系结构。要让学生体会数学模型的一般性特征，一方面要从具体、形象的实例或现实情境开始，通过多次的抽象、概括，建立数学模型；另一方面，也要通过思维发散和联想加以拓展和推广，赋予所教内容的“模型”意义。因此，教师在引领学生经历模型的建构过程中，让学生进行分析、比较、抽象和归纳等，逐步逼近数学模型的本质特征，在认知过程中建立起一种统摄性、符号化的“模型”载体，感悟数学模型的一般性。

例如，苏教版五年级上册《用字母表示数》的教学，教师首先从学生的生活入手创设情境并运用情境图：买1 个排球60 元，买2 个排球要2×60 元，买3 个排球要3×60 元……买10 个排球要多少元？买100个排球呢？买a 个排球多少元？当学生得出了60a 元后，将情境图去掉，让学生用自己的语言表达60a 的含义，即60a 表示什么？可以表示买一个排球吗？可以表示买10 个排球吗？可以表示买100 个排球吗？这里，学生在教师的追问中感受到“60a”这一模型的一般性。即60a 表示“单价×数量=总价”。当学生建构了数学模型之后，教师又引导学生运用结构化的思维，寻找类似的数量关系。“60a 还可以表示什么？”学生认为可以表示1 小时行的路程，也可以是10 小时行的路程……这里60a 还可以表示“速度×时间=路程”。教师适时引导学生理解这两种模型的本质联系，使学生结构化地掌握这两种模型。因此，学生理解了“单价”表示“1 袋多少元”“1 吨多少元”等，“速度”表示“1小时行多少千米”“1 分钟行多少米”等，“单价”“速度”都表示1 份数，“数量”“时间”都表示有这样的几份（份数），“总价”“路程”则表示一共有多少份（总数）。于是，“每份数×份数=总数”更上位的数学模型自然产生。借助这样一个数学模型，赋予“每份数×份数=总数”更多的“模型”意义，引导学生进行联想寻找生活原型。例如“工程队每天修路120 米，共修了8天，一共修了多少米？”“春梅家庭农场一共有12 公顷土地，今年每公顷大约产粮9 吨，一共产粮多少吨？”等等。通过实际运用，“每份数×份数=总数”这一数学模型的一般性、包摄力和表征力才能彰显出来，让学生充分体验到了数学模型的魅力。

二、多元表征——简约化

在教学中，教师应该引导学生从日常生活或真实情境中发现问题和提出问题、建立数学模型，让学生学会用数学符号表征数量关系和变化规律。数学模型的表征是学生个性化的解读与理解，有助于学生对数学模型内涵的认知和清晰化，有利于模型的推广。因此在数学建模过程中，教师应不失时机地引导学生尝试用符号语言建构和表征模型，充分体现数学模型的简约化。

例如，苏教版四年级下册《乘法分配律》的教学。学生前期例举了各种类型的例子来证明乘法分配律的可靠性。如何简洁地表示出乘法分配律，于是教师设计了“你能不能用一个式子表示这一运算律？”这样的问题引导学生思考。学生通过探索认为可以用“（几+几）×几=几×几+几×几”来表示这一运算律。但有学生认为这样的表达不够清楚和简洁，用几来表示，可以是任何数，这样写体现不出左边和右边的联系，认为可以改成“（□+△）×○=□×○+△×○”来表示这一运算律。教师及时让学生说一说这样表示的理由，因为□代表括号里的第一个加数，△代表第二个加数，○代表括号外面的乘数，可以写成括号里的两个数都和括号外的数乘一次，再相加。最后有学生认为这样表示还不够简洁，又提出了用字母表示的方法“（a+b）×c=a×c+b×c”，用a 和b 代表括号里的两个加数，c 代表括号外面的乘数。教师设计了“你更喜欢哪一种”这一问题让学生来评价这三种方法，让学生体验到用字母来表征乘法分配律更简洁，更容易书写。鼓励学生用字母表达所发现的运算律，使学生意识到乘法分配律的一般性，并经历体验由文字表达到图形表达再到符号表达的转化过程。让学生经历用字母表达运算律的学习过程，不仅培养了学生的符号意识，也让学生感受到了数学模型表征的简约化。

三、适度变式——结构化

数学模型的共同点都是由原型结构抽象出数学结构。建立模型的过程，本质上就是“数学化”的过程，在学习中获得某种带有“模型”意义的数学结构的过程。因此在教学中，教师要引导学生对已建立的数学模型进行适度变式，结合解决实际问题的教学，设计“多题一解”和“一题多变”的练习，有助于学生感悟模型间的联系，强化对模型的结构认知，体会数学结构的整体性。

1.多题一解

（1）水果超市的苹果比香蕉多200 千克，卖出的苹果是卖出香蕉的2 倍，这时苹果和香蕉都还剩100千克，卖出香蕉多少千克？

（2）水果超市的苹果比香蕉多200 千克，卖出的苹果是卖出香蕉的2 倍，这时苹果还剩100 千克，香蕉还剩150 千克，卖出香蕉多少千克？

（3）水果超市的苹果比香蕉多200 千克，卖出的苹果是卖出香蕉的2 倍，这时苹果还剩150 千克，香蕉还剩100 千克，卖出香蕉多少千克？

学生汇报：设卖出香蕉x 千克，卖出的苹果2x 千克。（1）（2x+100）－（x+100）=200；（2）（2x+100）－（x+150）=200；（3）（2x+150）－（x+100）=200。发现学生不约而同地都选择了方程，因为这三道题的数量关系是一致的，都是“苹果的质量－香蕉的质量=200 千克”，这样列方程就使问题解决变得很简单。不管条件怎么变化，只要数量关系（数学模型）不变，方程的框架就不变。

2.一题多变

（1）一辆汽车从甲地到乙地，共行了9 小时，前4小时每小时行85 千米，后5 小时每小时行105 千米，甲地到乙地一共有多少千米？

（2）鸿燕服装公司要生产一批衬衫，前3 天每天做105 件，后4 天每天做120件，一共做了多少件？

（3）工厂要购买一些煤，第一批运进了8 吨，每吨售价800 元，第二批运进了4 吨，每吨售价700 元，两批煤共需多少元？

三个实际问题虽然情节不同，但数量关系（数学模型）是相同的，都是求“两积之和”。学生通过这样的情境变换训练，多角度分析、比较看清了这些实际问题的本质，都具有相同的数学结构，掌握不变的数量关系（数学模型），就能以“不变”应“万变”，有助于学生体会不同问题中所蕴含的相同本质，感悟原型间的联系，感受数量关系（数学结构）的魅力。

四、经历演绎——应用性

人的认识过程是一个由感性认识上升到理性认识、再由理性认识回到实践的循环往复、螺旋上升的过程。数学模型意识的渗透应充分关注模型的具体应用，要引导学生从具体的问题抽象提炼出相应的数学模型，再从形式化的数学模型出发，将数学模型还原为具体的数学直观或可以感触的数学现实，使已经构建的数学模型不断得到丰富。让学生经历演绎的过程来解决实际问题，深刻理解数学的包容性和应用性，进一步提升数学应用能力，同时有助于加深学生对模型的理解，增强其应用数学模型的意识，体会模型的价值。

例如，针对苏教版四年级下册《三角形的三边关系》的教学，教师设计了基础性、拓展性、综合性三个层次的练习。

1.基础性应用

下面每组题中的3 条线段能围成三角形吗？（单位：厘米）

（1）4，10，6；（2）9，8，7；

（3）4，10，5；（4）6，7，10。

通过出示四组数据的线段，让学生判断能否围成三角形并做出合理的解释，对三角形三边关系的特征进行一个基础性的巩固与应用。在这里大部分学生都能准确进行判断，部分学生从中体会到三角形任意两边之和大于第三边，其实只要最短两条边之和大于第三边就可以，同时推理能力也得到进一步的提升。

2.拓展性应用

已知两条线段的长度分别是4 厘米和9 厘米，寻找第三边。

（1）另有长度分别为5 厘米、6 厘米、7 厘米、13厘米的线段，其中能够与前两条线段组成三角形的线段有哪几条？（学生独立思考，小组交流结果）

（2）第三条线段还可以是哪些长度（取整厘米数）？它最长是多少厘米？最短是多少厘米？（小组合作找出第三条边的所有可能，说说你是怎么想的）

本题需要逆向思考，如果教师一下子就把题目完整地抛出来，学生解题存在一定的困难。所以教师把问题分为两个小问题，通过第一个问题的铺垫，给学生作为思考的阶梯，利用已有的知识（三角形任意两边之和大于第三边）进行演绎推理选取合适的第三条边，长度可以是6 厘米和7 厘米；第二个问题，学生除了对第一个层次中得出的两短边之和大于第三边的体会更加深刻外，还发现与要保证两边之和有关系，那么两边之差也同样存在关系，三角形中两边之差必定小于第三边，合情推理与演绎推理相互融合。所以有部分学生得出了两个关系式即：4+9>第三边边长，9-4<第三边边长，并由这两个关系式轻松推导出第三条线段长度的取值范围：5 厘米<第三条线段的长度<13 厘米，即第三条线段的长度可以是6、7、8、9、10、11、12 厘米，其中最长是12 厘米，最短是6 厘米。

3.综合性应用

从学校到少年宫有几条路线？走哪一条路最近？

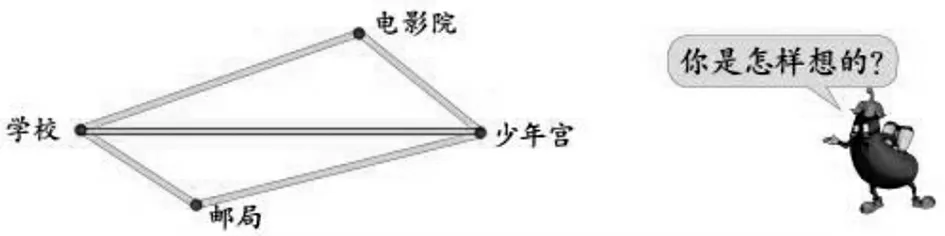
该练习的设计，将数学模型还原成具体的实际问题，让学生在解决问题的过程中加深对数学模型的理解。一方面让学生体会到通过探究得到的结论不仅可以解决数学上的问题，而且也能解决生活中的问题，使学生获得浓厚的学习兴趣与成就感，也为进一步渗透与培养模型意识打下良好的基础。另一方面，学生通过已有的知识（三角形的三边关系），又推出了一个新的结论：两点间线段最短。两个知识点得到了很好的融合。

数学模型不仅为数学表达和交流提供有效途径，也为解决现实问题提供重要工具，可以帮助学生准确、清晰地认识和理解数学的意义。我们要多措并举，以发展学生的模型意识为契机，渗透到知识的形成过程中，渗透到知识的应用中，渗透到学生思维过程中，从而更好地培养学生用数学的眼光来观察现实世界。