《铁链的长度》教学设计

文 高畅

【教学内容】

北京版六年级上册“数学百花园”。

【教学过程】

一、适当调节，轻松引入

视频播放飞夺泸定桥片段，红色教育进课堂，引出课题。

师：飞夺泸定桥不仅打开了红军长征的通道，还谱写了世界史上的战争奇迹。这场战役之所以这样惨烈，是因为它是在十三根铁链上完成的。你们看出来铁链是怎样连接而成的吗？用手比一比，就是由无数个铁环这样环环相扣。今天这节课我们就来一起研究铁链的长度。（板书课题）

二、创设情境，明确目标

（一）理解题意，揭示内容

师：这是其中一个铁环，通过观察知道了什么，还能想到什么？

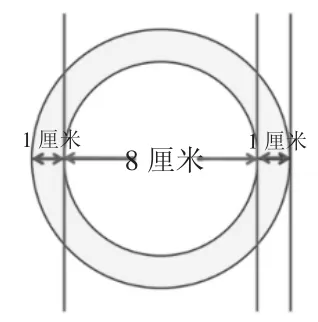
预设：外直径是10 厘米，内直径是8 厘米，环宽是1 厘米。

评价：同学们善于观察，描述得非常准确，挖掘出了隐藏的环宽。

（二）合理估算

过渡：那么100 个这样的铁环连接而成的铁链有多长呢？

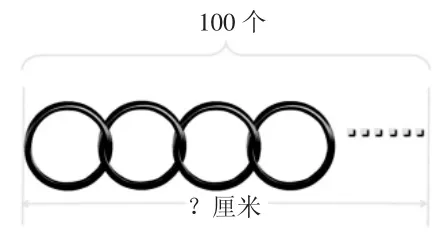
师：最长不会超过多少厘米？

预设：1000 厘米。

评价：你的空间感真好！

师：最短也不会少于多少厘米？

预设：800 厘米。

评价：分析得合情合理。

【设计意图：在估一估的过程中，培养学生的估算意识，能提高学生判断和选择的能力。对铁链长度的空间感、数感有整体感悟。在后面解决铁链长度的时候做到心中有数，便于自我反思规律结果的正确与否。】

三、团队学习，自主探究

（一）确定研究方法

师：那么100 个这样的铁环连接而成的铁链有多长呢？你打算怎么解决？

预设：从简单的开始研究。

引导：你和伟大的数学家华罗庚爷爷想到了一起，他说在解决数学难题时，我们要学会知难而“退”，退到最简单而又不失关键的地方。“退”就是从简单的开始研究，这样一来就化繁为简了。那我们从几个研究呢？

预设：从2 个开始研究。

评价：简单而又不失关键。

【设计意图：从简单关键处思考是化繁为简思想的本质，借用华罗庚的话引出这一数学方法，能提高学生对化繁为简思想的接受度，产生与名家数学思想共鸣的自豪感。给学生提供了一种解决探索规律问题的方向和策略，激发学生探索规律的兴趣和信心。】

（二）探究2 个圆环

师：现在形成铁链了吗？此时的长度？（动画演示）现在呢？此时铁链的长度是多少？请用手中学具，以小组为单位，研究一下2 个铁环连的铁链长度是多少。

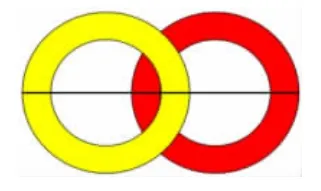
1.交流展示

预设：

（1）（假设法）我们组得到的是18 厘米，假设2 个铁环是分开的，那总长度也就是2 个10，减去重合的2 厘米，即2 个环宽，结果为18 厘米。（10×2-2）

评价：太喜欢他们的表达了，能边指边说，他们口中的这2 个环宽也可以说成是一个环扣。

（2）（分类1）从中间切开，第一个铁环少了1 厘米，第二个也少了1 厘米，就得到2 个9，所以是18 厘米。（10+8）

评价：用拆分的思想从环扣中间切开，很新颖。

（3）（分类2）第一个圆环10厘米，剩下的部分是8 厘米。

评价：特别喜欢同学们在不断地深入思考中求异、创新。

（4）（分类3）2 个铁环的内直径连在一起8×2=16 厘米，再加上2 个环环宽1×2=2 厘米，共18 厘米。

评价：他们能从别人的方法当中得到启发，真会倾听和思考。

2.总结归纳

师：太了不起了！简单的2 个铁环，大家想到了这么多种方法。接下来，咱们整体回顾一下这几种方法，请看大屏幕。

总结：第一种方法是假设2个铁环分开，这样总长度就是10×2，也就是2 个外直径的和，减2个环宽也可以说成是减去一个环扣。所以这种方法可以简单概括为“2 个外直径-一个环扣”。

总结：这种方法中10 就是铁环的外直径，8 表示的是剩下的长度。所以就是“一个外直径+8”。

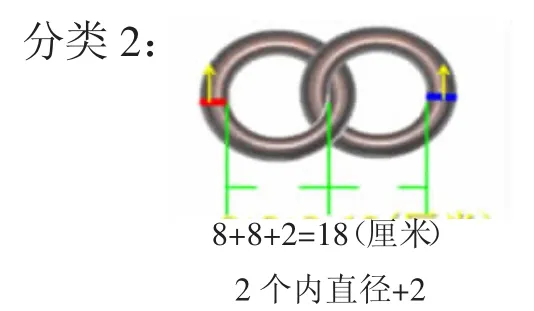
总结：这个方法中的2 个8其实就是2 个内直径，还剩下两边的环宽，所以是“8×2+2”。

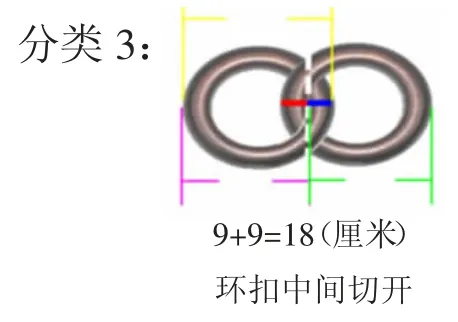
总结：这种方法就是把环扣从中间切开，让左右变成了相等的两部分。

【设计意图：借助手、纸质圆环、电脑动态显示等一系列学具和演示，将2 个环相扣的问题几何直观化。目的是让学生回到图中找依据，让直观学具和动态演示成为学生建构理解铁链连接处特点的有力抓手，帮助学生观察、理解环扣的结构特点。回顾学生观察结果，总结多种观察方法，能够启迪学生思路，拓展学生思维，将感性思维理性化、结构化，为下面解决铁链问题建模归纳做铺垫。】

（三）合作探究多个圆环，发现规律

1. 小组合作研究3、4、5……100 个圆环

引导：研究完2 个接下来怎么办？（研究3 个）一直研究下去吗？（发现规律之后就不用研究了）请大家看合作要求：

（1）小组内快速从四种方法中选一种，把算式写在《报告单》中。

（2）继续用你们选的这种方法，试着研究3 个、4 个……

（3）结合标注和算式，看看有什么发现。

（4）发现规律后，计算100 个铁环连接成的铁链的长度。

师：哪个组想分享发现的规律？是怎样发现的？给大家讲讲这个算式的意思。

预设1：3 个铁环有2 个连接处，1 个连接处少2 厘米，一共少4 厘米，30－4=26（厘米）；4 个铁环是40 厘米，连起来后有3 个连接处，每个连接处少2 厘米，则40-2×3=34（厘米）。结论是几个铁环铁链的长度为10n-2（n-1）。

评价：有理有据，条理清晰。就是n 个外直径-（n-1）环扣。

预设2：3 个铁环：还是把第一个当标准，也就是10 加上2 个8，10＋8＋8=26（厘米）；4 个铁环：同理，1 个铁环10 厘米再加上3 个8是10＋8×3。规律是10+8（n-1）。

评价：语言真准确，把第一个当标准这样分类就方便观察了。

总结：这种规律可以概括为1个外直径+8（n-1），把第一当标准。

预设3：两边都是环宽，再加上中间的8 厘米就是铁环的长度了1＋8×n+1。

预设4：3 个铁环：两边的铁环是9 厘米，中间的只剩下内直径8 厘米，9+8+9=26（厘米）；4 个铁环：两边的是9 厘米，中间2 个是8 厘米，9＋8＋8＋9=34（厘米）；100 个铁环：9＋8×98＋9=802（厘米）。规律是9+8（n-2）+9。

总结：你最喜欢哪一种，为什么？你最容易理解的就是最适合你的。

【设计意图：化繁为简、层层深入地去探究，产生思维的碰撞，在合作的过程中逐渐抽丝剥茧总结出规律，并应用规律顺利解决问题，目的是让学生真正经历化繁为简的过程，积累探索规律的经验，感悟化繁为简方法的优点。而多种方法的交流，发展了学生的数学推理、分析、表达能力，更能拓宽学生思维，提高学生解决问题的灵活性，发展创新个性化数学思维，让学生在解决问题的过程中深刻感悟，解决同一个问题的多种策略。】

2.回顾过程，总结方法

师：回顾研究过程，我们怎样解决铁链长度这个问题的？

生：利用化繁为简的方法，从最简单的开始，通过对2 个、3 个、4 个铁环相连的图形进行观察、分析、推理，最终归纳出了规律，再利用规律解决问题。

师：你觉得今天的学习对以后解决复杂问题有什么帮助？

生：遇到难题别着急，先从简单的开始研究。

总结：运用这些学习方法可以帮助我们解决很多问题，比如摆小棒问题、图形递增问题、曲线累加问题、桌椅问题……

【本文为“第十五届全国小学教学特色设计论文大赛”获奖作品】