基于超螺旋滑模控制的LCL三相逆变器离网扰动抑制策略

晋秉义,于 凯,李 强,张 伟

(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012;2.吉林市桔凯科技有限责任公司,吉林 吉林 132012;3.国网四川省电力公司绵阳供电公司,四川 绵阳 621000)

0 引 言

近年来随着电网规模的迅速扩大以及对电力需求和可靠性的要求不断提高,传统电力系统技术难以解决运行控制一致性问题。因此分布式发电(Distributed Generation,DG)、微电网(Micro-Grid)已经成为世界各国的研究重点。在我国分布广泛的分布式发电单元接入微电网已逐渐成为电力系统的重要发电方式之一[1],因其具备较高的灵活性和可控性,使微电网在维持电网的稳定性和可靠性方面发挥重要作用[2]。微电网在孤岛模式下运行时,由于分布式发电系统存在间歇性、负载之间的功率差异以及其他不确定因素,存在诸多不确定性和外部扰动,电压和频率可能会出现畸变,从而影响微网系统稳定性和系统运行[3]。

离网运行过程中会受到若干不确定性的影响,系统中各电气量也会随之产生波动,从而偏离其设定的参考值使系统误差增大。在滤波电容电感以及内部阻抗实际设计中会出现细微偏差从而偏离额定值,随机变量参数越多对系统的输出结果影响越大,因此系统控制方法要对于滤波参数的不确定性能有抗干扰能力;系统运行过程中多用户频繁投切负载或者存在大功率用电设备的投切会导致三相电压电流突变,如果系统不及时恢复稳定会影响用电设备正常运行,而突变超过一定的限值,则会造成电气故障;分布式发电设备由于其自身不稳定、可靠性不高以及运行经验等因素,在检修切除或遭遇自然灾害发生损坏时会影响整体系统的直流电压输入。

对于孤岛微电网来说,控制系统的主要目标是在系统正常运行或遭遇较大的负荷扰动时,均可维持电压、功率在其额定值或参考值附近。微电网在孤岛模式下需要一种精确的控制来抑制系统的不确定性扰动和提升系统的动态响应能力,文献[4-5]使用模型预测控制抑制三相逆变器扰动,采用扰动观测器来简化预测模型,该方法无需系统内环从而拥有更好的鲁棒性和动态响应。但模型的精确度对模型预测控制的影响较大,需要极高的准确度,并且建模过程复杂,计算量大,不能满足实时控制的系统要求。

另一种控制思路是改进下垂控制环的方法[6-8]来实现系统扰动抑制和动态特性提升。文献[6]提出一种新型的下垂控制方法,在传统下垂内外环控制中加入动态虚拟阻抗反馈以及在传统功率控制环中引入积分控制的方法,并使用PI控制器修正下垂系数,提升了系统的动态稳定性;文献[8]提出了一种新型并联逆变器负荷控制器,通过改进下垂方程,在传统的下垂控制方程中引入导数和积分环节提升系统的动态响应和系统可控能力。

滑模控制(Sliding Mode Control,SMC)是一种动态响应快,抗外部扰动以及鲁棒性强的控制方法,尤其适用于易受到外部扰动和参数不确定的情况,但抖振现象是滑模控制最大的缺点,会影响系统稳定运行甚至损坏仪器。而高阶滑模控制在保留了传统滑模控制优点的基础上可以抑制抖振现象,同时除去了相对阶的限制并提高了系统精度[9]。在文献[10]中讨论了几种不同的高阶滑模控制方法例如超螺旋算法(Super-Twisting Algorithm,STA)、漂移算法、次优化算法和收敛算法,均可以提升系统的动态响应和谐波抑制能力,在上述几种算法中,STA在计算中所需已知信息少,只需要已知滑模变量的值就可以计算,结构简单并且计算速度较快,因此STA拥有较强的优势,可以消除参数不确定性和外部扰动带来的影响。文献[12]在三电平逆变器与三相并网逆变器电压外环和功率跟踪环中加入超螺旋控制,并且在电压调节器中加入可开关式高增益观测器防止外部干扰影响控制性能,该方法对比普通滑模控制拥有较强的抗扰能力和更快的瞬态响应;文献[14]提出一种新型的鲁棒非线性超螺旋控制器,通过将STA和传统滑模控制相结合的方式设计控制器,针对单相逆变器的分布式电源,同时考虑孤岛和并网两种运行情况,均可保证系统在各种负载情况下的稳定性和鲁棒性。

在上述方法中,预测控制、改进下垂控制和滑模控制均可提升系统的动态响应和鲁棒特性。超螺旋滑模控制方法在逆变控制中体现出较强的优势,针对传统PI控制的LCL三相逆变器负载扰动抑制能力较弱以及电压参考跟踪速度慢的缺点,本文将利用超螺旋滑模控制方法的优异性能,设计三相逆变器的内外环。在dq坐标系下,基于内模原理分别设计系统内外环STA控制器,并根据Lyapunov函数证明系统的稳定性,在不同的滤波参数条件下验证系统的鲁棒性能,仿真结果证明了本方法对参数不确定性具有较强的鲁棒性;本文提出的控制方法对比传统的PI控制,在不同工况下的孤岛半实物实验结果表明,该方法可将波动抑制在半个工频周期内,可以有效抑制负载突变引起的干扰并提升响应速度。

1 离网型逆变器的拓扑结构与控制策略

1.1 主电路拓扑与数学模型

图1为LCL型三相逆变器离网电路模型。其中,Vdc为直流源电压;V1～V6为三相桥的6个IGBT开关管,忽略滤波电感和电容的电压损失,L1、C、L2构成三相LCL型离网逆变器的滤波结构;R1,R2分别为逆变侧和负载侧等效电阻;u1x为逆变器输出的未经过滤波的电压;i1x为逆变器侧电流;uCx为滤波电容电压;i2x为负载侧电流;Rx为三相负载,x=a、b、c。

图1 三相LCL型孤岛逆变器拓扑Fig.1 Topology of three-phase LCL islanded inverter

假设主电路拓扑结构为三相平衡负载且开关器件均为理想元件,根据KCL和KVL方程得到abc三相静止坐标系下的电压电流方程:

(1)

公式中:uk为负载电压,k=a、b、c

由于同一时刻相同桥臂仅有一个开关管开通,记开通时为1,关闭时为0;设三相逆变器的上桥臂的三个IGBT(V1,V3,V5)的开关状态为δa1、δb1、δc1,下桥臂的三个IGBT(V2,V4,V6)的开关状态为δa2、δb2、δc2,开关状态满足下式:

δk1+δk2=1

(2)

假设δk=δk1=1-δk2,逆变器输出线电压与直流电压源Vdc的关系为

(3)

根据abc三相静止坐标系下的电压电流方程,得到LCL三相逆变器的数学模型如图2所示。

由于在abc三相静止坐标系下控制量均为交流量,且缺少零序分量以及控制量复杂,因此通常将三相系统变换到两相系统分析。考虑到控制器对直流量分析时可以减轻控制器的复杂程度,并且可以对有功功率和无功功率进行单独控制,因此本文考虑使用Park变换将abc三相静止坐标变换到dq两相旋转坐标系下,3s/2r的坐标变换公式如下:

(4)

公式中:θ为d轴与相位参考轴的夹角。将公式(1)、公式(3)和公式(4)化简得到dq坐标系下的电压电流方程

(5)

(6)

(7)

公式中:w为三相电压的基波角频率。由公式(5)、公式(6)和公式(7)可以看出dq轴状态量相互耦合,这会影响闭环控制的电流跟踪效果[15]。为了消除耦合量对双环输出的影响,通常在双环PI控制器中引入前馈解耦控制从而保证dq轴的单独控制,这将增加大量微分运算和其他控制参数,导致系统运算复杂,系统整体性能将会受到每个参数准确性的影响,难以达到理论效果。dq坐标系的数学模型控制框图如图3所示。

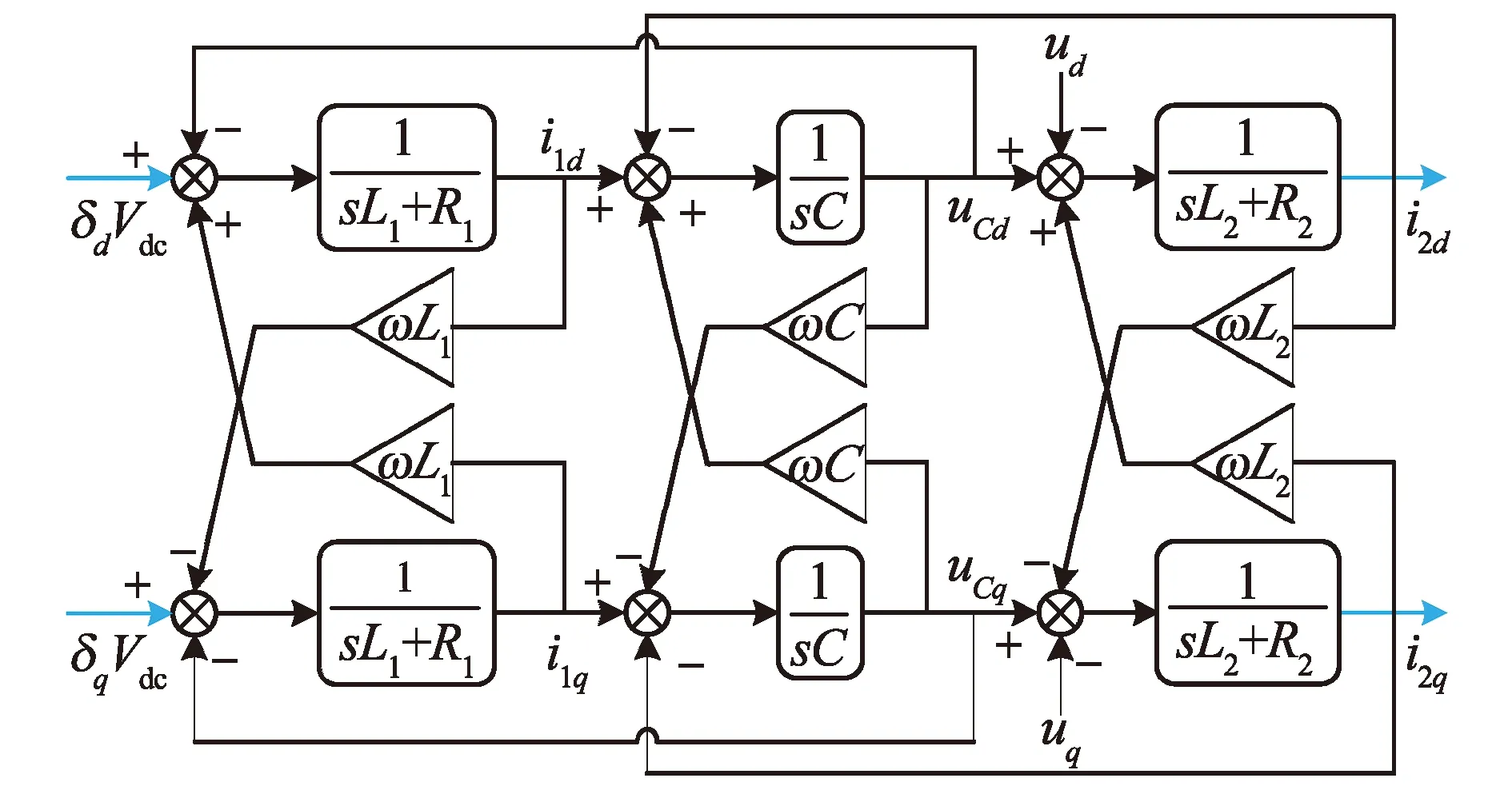
图3 LCL型逆变器dq坐标系控制框图Fig.3 Dq coordinate system control block diagram of LCL inverter

1.2 功率环控制

系统的功率外环采用下垂控制方法,根据系统的输出电压和电流计算电压参考。下垂控制器使用dq旋转坐标系的平均法计算,通过输出侧在dq轴采样的电压电流计算三相有功功率和无功功率

(8)

本文考虑逆变器等效输出阻抗阻性远大于感性,因此考虑使用阻性下垂方程,下垂方程的电压参考和频率参考的计算如下:

(9)

公式中:V、ω、P和Q分别为逆变器输出电压幅值参考、角频率参考有功功率和无功功率;kp和kq分别为有功下垂系数和无功下垂系数,Vref、ωref、Pref、Qref分别为额定电压幅值、额定角频率、额定有功功率和额定无功功率。dq坐标系下的坐标转换公式为

(10)

根据公式(4)得到dq坐标系下的电压,三相逆变器阻性下垂控制的控制框图如图4所示。利用dq轴的输出电压和电流计算三相有功和无功功率,并使用下垂方程式计算dq轴的参考电压用于电压外环计算。

图4 下垂控制策略框图Fig.4 Block diagram of droop-control strategy

2 双环控制策略

2.1 超螺旋算法

首先给定二阶系统如下

(11)

公式中:φ(t,x)和g(t,x)为包含时间t,变量x和控制函数u的有界未知函数,边界值满足:

(12)

公式中:F、Γmin、Γmax为正常数,在满足边界值条件下的滑模变量s(t,x)的微分包括:

(13)

本文使用的STA控制器如下[16,17]。

(14)

公式中:s为滑模变量;l和a分别为待设计的控制参数;sign(s)为符号函数。本文为了进一步减少抖振,通过将超螺旋控制器中的不连续的符号函数sign(s)替换为连续的tanh(s)函数,换句话说,tanh(s)函数被用作符号函数的近似值[18]。

(15)

(16)

通过公式(16)可以看出滑模量s及其导数将在有限时间内收敛至0且出现的两个开关函数都不会影响系统的滑模特性。λ和α满足边界条件(12)的限制,那么滑模量s在有限时间内稳定的充分条件为[19]

(17)

2.2 双环设计

2.2.1 电容电压外环

由于电感电流环的控制带宽远大于电容电压环的控制带宽,因此可单独设计双环的控制结构。

首先对电容电压外环的滑模变量定义如下:

(18)

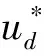
(19)

对公式(18)求一次微分并联立公式(19)可得:

(20)

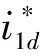
(21)

公式中:μv(svd)和μv(svq)分别为电压滑模控制器;C0为滤波电容C的额定值。

根据公式(16),μv(svd)和μv(svq)可以写为

(22)

公式中:λvd、λvq、avd、avq分别为大于0的比例积分系数。根据公式(20)和公式(21)得到滑模变量svd和svq的动态方程

(23)

公式中:ΔC为滤波电容的不确定量,ΔC=C-C0。因此ΔC为有界量,则存在两个正常数Cvn1和Cvn2满足约束条件:

(24)

根据公式(17),滑模变量svd和svq能够在有限时间内收敛于滑模面svd=dsvd/dt=0和svq=dsvq/dt=0的充分条件是[19]

(25)

2.2.2 电感电流内环

对电感电流内环的滑模变量定义如下:

(26)

(27)

公式中:μi(sid)和μi(siq)分别为电流滑模控制器;L10为滤波电感L1的额定值。

根据公式(16),μi(sid)和μi(siq)可以写为

(28)

公式中:λid、λiq、aid、aiq分别为大于0的比例积分系数。根据公式(5)、公式(26)和公式(27),滑模变量svd和svq的动态方程为

(29)

公式中:ΔL1为滤波电感的不确定量,ΔL1=L1-L10。因此ΔL1为有界量,存在正常数L1n1和L1n2满足约束条件:

(30)

根据公式(30),滑模变量sid和siq能在有限时间内收敛于滑模面sid=dsid/dt=0和siq=dsiq/dt=0的充分条件是[19]:

(31)

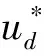
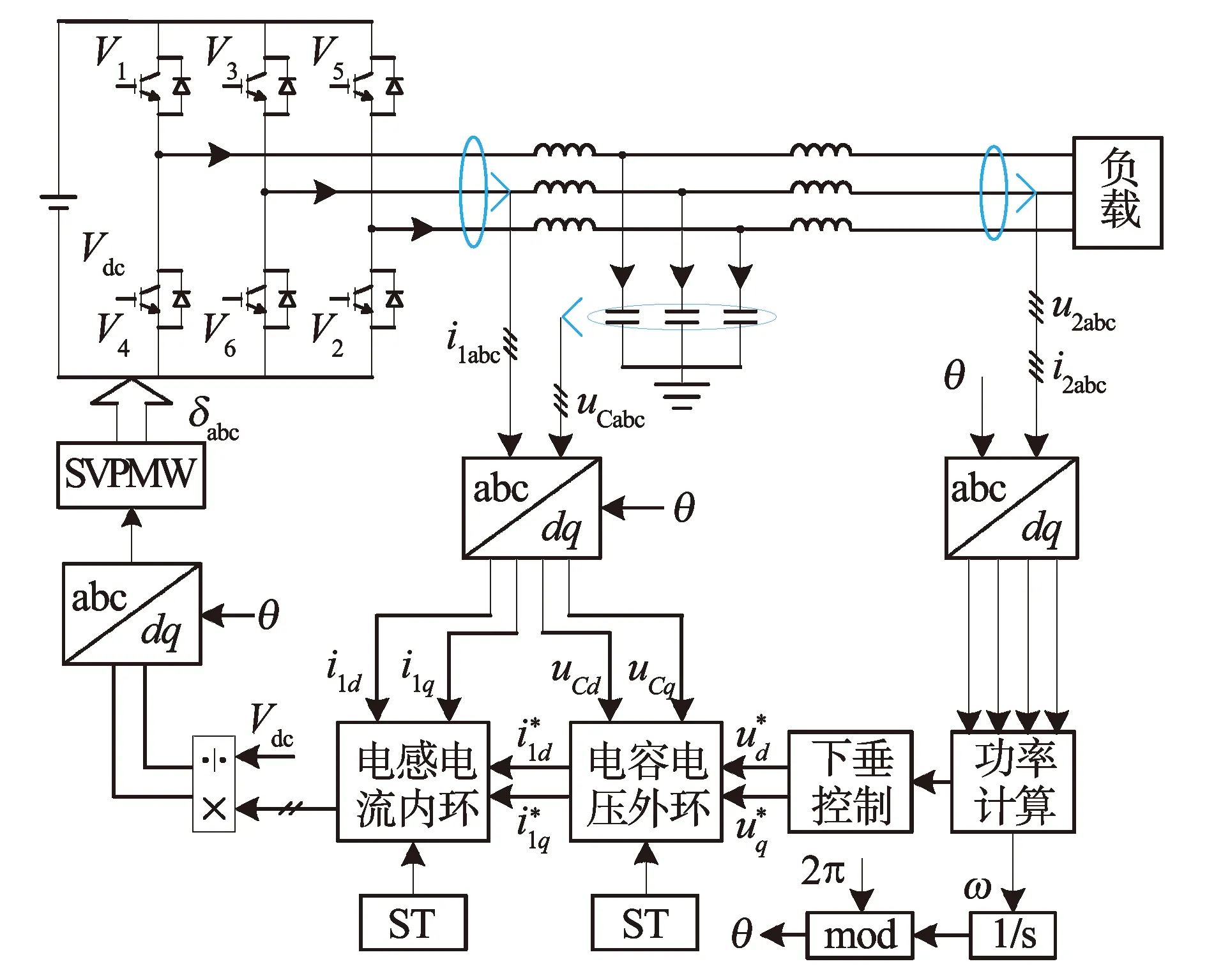
图5 基于STA的三相逆变系统扰动抑制策略整体控制框图Fig.5 Overall structure block diagram of disturbance rejection strategy for three-phase inverter system based on STA

观察超螺旋双环控制方程公式(21)及公式(27),源自于超螺旋控制方法的本质,电压环设计中包含输出电流i2d,电流环设计中包含uCd,作为前馈项可以提升系统的抗扰动性能、参考变化响应,对比传统滑模控制,“前馈”量的引入会使超螺旋控制增益μv(sv)和μi(si)变小,在控制系统中充当精确调整的作用,并且由于超螺旋算法的有限时间收敛特性,将不会影响系统到达稳态的响应速度。

2.3 稳定性分析

为证明本文基于STA的双环控制系统稳定性,选择公式(32)作为电压环的Lyapunov候选函数[20]

(32)

对公式(32)求微分并联立公式(18)～公式(22)可得:

(33)

当滑模变量svd>0时,双曲正切函数tanh(s)>0,则有dRvd/dt<0,反之svd<0时,tanh(s)<0,则dRvd/dt>0,因此Lyapunov函数RV(sv)正定且关于时间的一阶导数负定,证明滑模变量svd可以渐进收敛至0,即证明本文提出的基于STA的电压环控制器渐近稳定,同理可证明电流环的稳定性。

2.4 鲁棒性分析

在分布式发电系统中会出现难以预测的测量噪音、系统内部的电磁场辐射感应,器件导线间的分布电容、分布电感引起的耦合感应以及滤波元件实际参数与额定参数之间的误差,会对整体系统稳定性产生影响,考虑到多种不确定性,将电压外环的滑模变量(23)修改为如下

(34)

公式中:ξ为系统的内外部扰动之和。则公式(33)可以修改为

(35)

根据Lyapunov稳定性条件,只要λv和αv参数合理选择即可实现函数RV(sv)对时间的一阶导数负定,本文提出的基于STA的双环控制器拥有较强的鲁棒性。

3 仿真及实验

3.1 鲁棒性能仿真

仿真基于PLECS平台,验证本文提出的基于STA控制方法对系统滤波参数的不确定性具有鲁棒性,仿真与实验平台系统参数设计如表1所示。

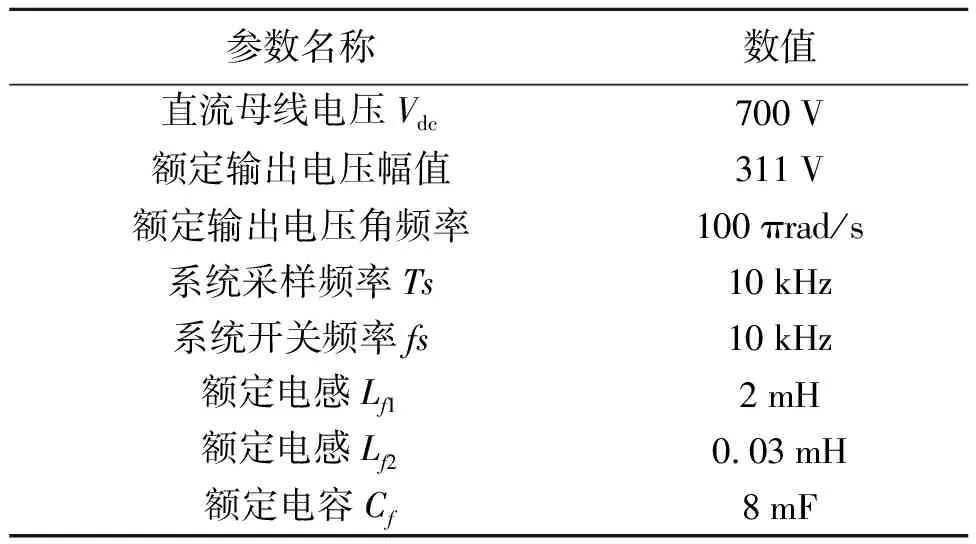
表1 基于STA的三相逆变器鲁棒性仿真测试参数

图6为在相同控制参数情况下的三种不同工况下的鲁棒性仿真结果,额定功率为3 kW,其中图6(a)中工况Ⅰ对应为额定滤波参数的A相输出电压波形;工况Ⅱ为1.5倍额定滤波参数;工况Ⅲ为2倍额定滤波参数。输出有效值作为本方法的控制精度参考,通过图6(a)可以看出三种工况下的A相电压和电流波形没有出现任何波动,系统并未受到滤波参数扰动带来的影响,且输出电流可以快速跟踪负载投切的变化。观察图6(b),随着滤波参数变化系统输出电压有效值出现较小偏差值约为0.22 V(工况Ⅱ),当2倍额定滤波参数时出现约1.2 V的电压波动,在约1.2个额定周期(24 ms)后到达稳态。仿真结果表明即使系统出现两倍的滤波参数扰动,对系统输出电压也仅会产生较小影响。以上仿真结果证明了本文提出的基于STA的三相离网逆变系统对滤波参数扰动具有较好的鲁棒特性。

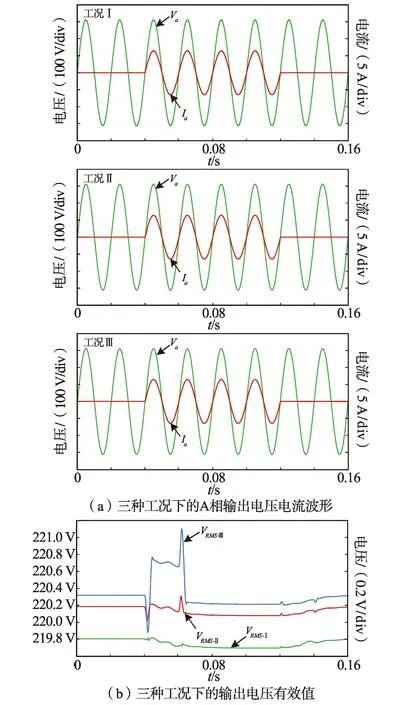
图6 滤波参数不确定性鲁棒性仿真Fig.6 Robust simulation results of filter parameters uncertainty

3.2 负载突变实验对比

为进一步验证本文使用的STA控制方法的抗干扰能力和响应速度,搭建了如图7所示的三相LCL逆变器系统实验样机。直流电源采用Chroma 62150H-1000S,电压和电流信号分别由LEM LV25-P电压霍尔、HLSR 32-P电流霍尔采样;通过瑞士Plexim GmbH公司开发的RT Box、PLECS仿真软件和PC进行验证。

图7 三相LCL逆变器实验平台Fig.7 Experimental platform of three-phase LCL inverter

图8和图9为两种控制方法的负载投切A相电压、电流、有功和电压有效值的实验波形,观察图8(a),在t1时刻投入负载,ST控制的输出电压和电流能迅速达到稳态值6.19 A,但PI控制的电压电流波形存在波动(峰值电压从311.5 V降低至298.9 V),约一个周期后趋于稳定(约20 ms)。图8(b)中使用ST控制的输出电压有效值最大波动仅为0.3 V,几乎不存在电压波动和功率波动,而PI控制方法电压有效值偏差达到约10 V,且需要约一个周期才能过渡到稳态。

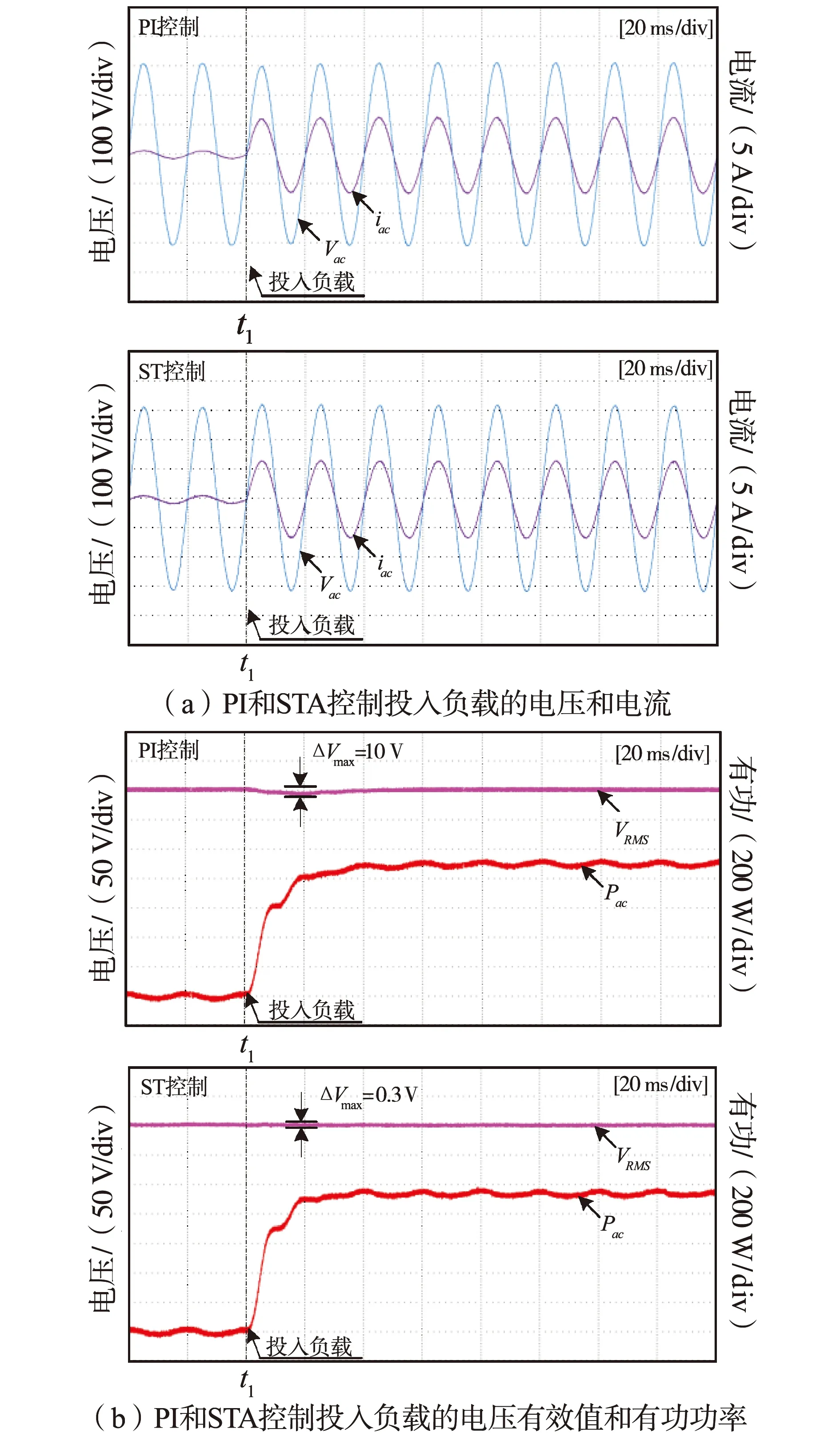
图8 三相逆变器扰动抑制策略投入负载对比实验Fig.8 Experimental results of load input comparison of disturbance suppression strategy in three-phase inverter

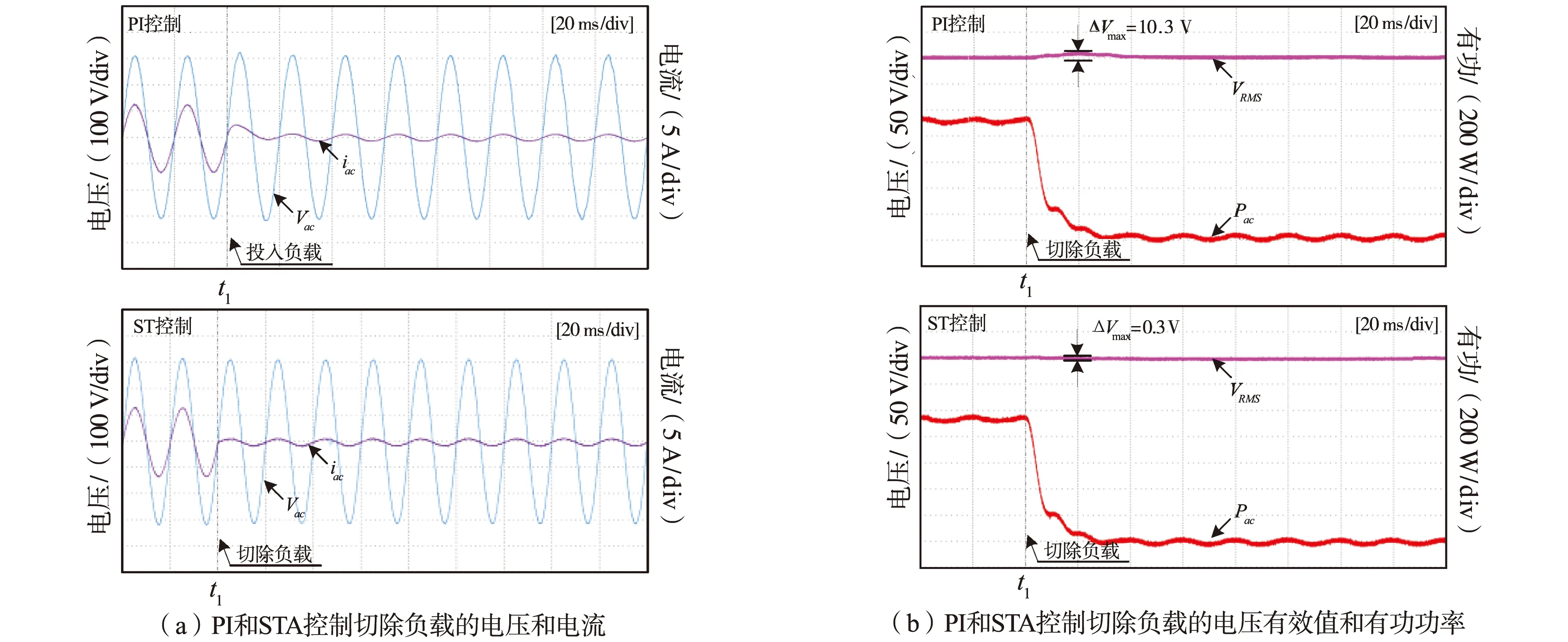
图9 三相逆变器扰动抑制策略切除负载对比实验Fig.9 Experimental results of load removal comparison of disturbance suppression strategy in three-phase inverter

对比图9(a),在负载切除时,PI控制的输出电压电流存在一个周期(约20 ms)的波动,ST控制的输出电压和电流可以快速过渡到稳态,无明显电压电流过冲。在图9(b)中PI控制的电压有效值在负载切除后存在约10.3 V的电压波动,而ST控制的电压有效值波动仅0.3 V。通过负载投切的对比图,本文提出的基于ST控制的三相逆变系统在负载投入和切除的瞬间,在孤岛工况下具有良好的动态响应过程并可以抑制系统负载扰动引起的变化。

3.3 参考突变对比

图10和图11为两种控制方法的参考突变A相实验对比。观察图10(a)的输出电压电流波形,在t1时刻参考电压突降30 V时,本文提出的ST控制的电压电流可以迅速跟踪电压参考,而传统PI控制的电压电流波形虽然可以跟踪电压参考变化,但要经过约2个周期(40 ms)才达到稳态,动态过程较长,同时存在跟踪误差。对比图10(b)的输出电压有效值和有功功率可以发现,PI控制经过约2个周期(40 ms)跟踪上电压参考变化,而ST控制有功功率波动很小且能在一个周期内(20 ms)快速跟踪电压参考变化。

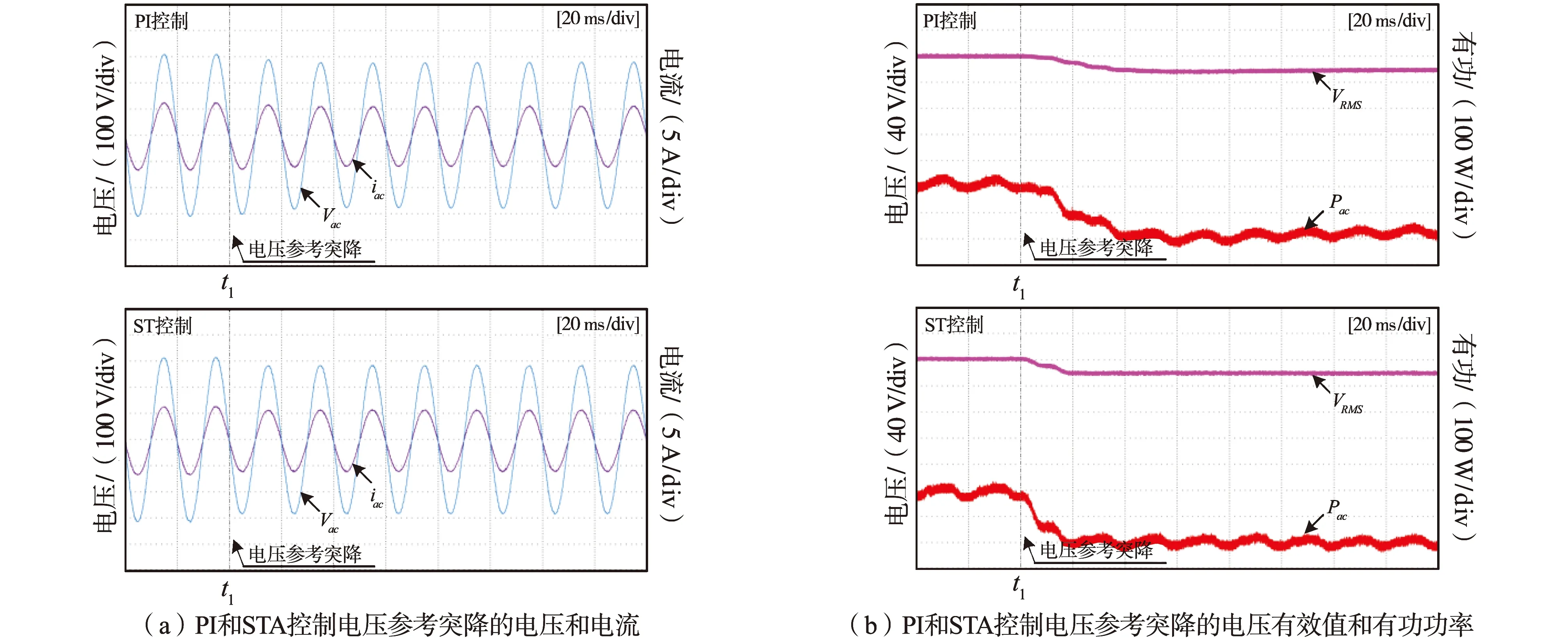
图10 三相逆变器扰动抑制策略电压参考突降对比实验Fig.10 Comparative experimental results of voltage reference drop for disturbance rejection strategy in three-phase inverter

图11 三相逆变器扰动抑制策略电压参考突升对比实验Fig.11 Comparative experimental results of voltage reference jump for disturbance rejection strategy in three-phase inverter

通过观察图11(a)可以看出,当参考电压突然恢复至额定电压参考时,PI控制输出的电压电流波形约经过约2个周期(40 ms)后才跟踪上额定电压,本文提出的基于ST控制的输出电压电流可以实现零误差跟踪参考电压。图10和图11实验结果表明,参考电压变化对本文提出的基于ST控制的三相逆变系统几乎无影响,几乎可以消除跟踪电压参考的过程,对比传统PI控制方法,在实际应用中可以减少系统电压电流以及功率波动,提升系统稳定性。

4 结 论

本文从内模控制基本原理出发,在dq坐标系设计超螺旋滑模控制数学模型,由于控制器中引入了输出电压和电流作为前馈变量,可以有效改善系统响应速度和抗干扰能力。通过与传统PI控制对比,证明了本文提出的扰动抑制方法对滤波参数的不确定性具有较好的鲁棒特性;此外在负载突变和电压参考突变实验中验证了本文提出的基于超螺旋滑模控制的离网扰动抑制策略的有效性,电压电流的动态变化过程可以快速跟踪负载或电压参考的变化,并可以有效抑制各种扰动带来的系统波动。