基于改进的AHP-CRITIC综合权重计算法的多元用户用能行为特性刻画及评价方法

朱 辉,闫腾飞,丁 一,程晓艳,盛耀龙,陈海鹏

(1.国网山东省电力公司聊城供电公司,山东 聊城 252000;2.东北电力大学电气工程学院,吉林 吉林 132012)

0 引 言

目前电力市场不断发展,电力用户在能源交易市场中的市场主体地位日益提高。因此,电力企业需要更好地了解和掌握工业用户用电规律,以提高其服务水平和市场竞争力[1]。与此同时,在综合能源系统快速发展的环境下,电力消费主体的多元化程度越来越高,对于生成用户用能行为画像的数据分析算法也提出了更高的要求[2-3]。随着智能量测终端的大量投用使用,工业用户用能数据得以实时采集,从而可以通过多元量测数据更准确地描述工业用户用能习惯与行为特性[4]。利用多元量测数据生成的“工业用户用能画像”可以再现工业用户用能的全貌,并为优化工业用户能源结构、挖掘工业用户需求特证、提高工业用户科学用能水平奠定基础条件。

用户画像是根据用户生活习惯、社会属性和消费行为等信息抽象出的一个标签化的用户模型,为了生成精细、智能与全面的用能画像,需要建立全面、客观的用户用能评价体系[5]。

针对多元用户的用能评估体系,国内外均有相关研究。文献[6]评估体系从技术性、经济性以及可靠性等多个层面展开构建;文献[7]从电压、负荷和综合三类维度构建评估指标,用以描述重要电力客户的用电状态。目前建立用户用能评价体系通常选取与电力相关联的指标建立。然而,在“碳达峰,碳中和”的背景下,有关用户低碳用能指标的用户用能评价体系相对欠缺。

确定用户画像是一个复杂的多目标决策问题,需要采用层次分析法(Analytic Hierarchy Process,AHP)、模糊综合评价、熵权法以及基于指标相关性的客观指标权重确定法等一系列方法来生成用户画像;在文献[8]中,采用层次分析法确定指标权重并计算综合用能指数,生成了工业用户多维用能画像;文献[9]构建电力用户的标签体系,并计算不同标签的权重,实现了用户画像的生成。使用层次分析法确定指标权重,主要采用多个专家打分确定标签权重,但但这种方法存在着赋权结果主观性较强、实用性较低的问题[10];文献[11]采用层次分析法和熵权法计算变压器状态评价体系中不同指标的综合权重;文献[12]采用客观权重赋权法对各项指标进行加权计算,从而实现用户综合用能画像,但在该文献中,只考虑客观因素时各指标权重的差异并不明显,无法足以体现出不同类型工业行业用户的用能特点。

针对上述问题,本文提出一种多层的工业用户用能评价体系,该体系从用电负荷水平、用电低碳指标、用电稳定性、用电互动能力以及用热/冷特性这六个维度综合评价用户用能水平,并且采用改进的AHP-CRITIC综合权重计算法对工业用户用能进行组合赋权,最终生成考虑用户用能特性的多元用户用能画像。本文基于四种工业用户用能数据完成算例分析,结果表明,本文提出的方法可以展现不同类型工业用户用能的差异性,从而帮助不同类型工业用户进行针对性的用能管理与服务政策。

1 多层用户用能评价体系建立

根据对国内外大型能源用户用电评价指标的广泛调研分析,并结合"双碳"目标本文构建了含有电负荷水平、用能低碳性、用电稳定性、用电互动性、用热(冷)特性等指标的工业用户用能特性评价体系,从而实现对不同工业用户用能特性的全面刻画,构建的工业用户用能评价体系如图1所示。

图1 针对工业用户的多元用户用能评价体系Fig.1 Multi-user energy use evaluation system for industrial users

1.1 用电负荷水平L1

用电负荷水平指的是工业用户在某个时间段内所需的用电量,包括日平均负荷、日负荷率、峰时耗电量以及谷电系数四个二级指标,作为反映工业用户负荷情况的评价指标[13]。

1.2 用电低碳性L2

用电低碳性指标反映了工业用户在可再生能源消纳和能源低碳转型方面的能力,主要包括清洁能源占比、减排率、余能利用率、电能替代水平以及废气达标水平五个二级指标[14]。

1.3 用电稳定性L3

在评估用户用电稳定性时,需要考虑电负荷变化幅度、趋势和波动等因素,最终选取日峰谷差、细节波动和日负荷波动率等指标来评估用电稳定性。

1.4 用电互动能力指标L4

用电互动能力是指在电力市场供需平衡背景下,对用户电负荷参与需求响应的潜力评估,主要包括调峰能力和需求响应潜力两个二级指标。

1.5 用热(冷)特性L5

在描述热(冷)负荷特性时,需求考虑其负荷水平和负荷稳定性。基于此,用热(冷)特性指标主要包括日平均负荷、日负荷率、峰时用能率以及日峰谷差四个二级指标[15]。

2 改进的AHP-CRITIC综合指标权重的计算

2.1 主观权重计算-FAHP法

模糊层次分析法(FAHP)是一种综合模糊数学和层次分析法的权重计算方法,在处理复杂评价系统中具有广泛应用。相对于传统的层次分析法(AHP),FAHP在处理涉及大量评估指标的项目时,能够更好地保证评价过程的一致性。通过引入模糊数学理论,FAHP能够处理评估指标的模糊性和不确定性,从而有效解决指标权重的一致性问题[16]。该方法的优点在于结合了模糊数学的灵活性和层次分析法的结构化特征,提高了评价结果的可靠性和准确性。

2.2 FAHP流程

2.2.1 层次结构模型

为了确定评价指标权重,首先确定评价体系的决策目标并且分析影响因素,接着构建层次化结构模型,最后从用电负荷水平、用电低碳性、用电稳定性、用电互动性、用热(冷)特性五个方面建立多层用户用能评估体系。该体系包括评估结果输出层、中间层和决策层。评估结果输出层的目标是多元用户用能水平综合得分。中间层涉及评价因素之间的关系。决策层确定系统的总目标,方案层表示用户各子指标的状态值。评价指标体系B由n个指标组成,即B={B1,B2,...,Bn}。每个指标Bi可能包含s个子指标,即Bi={Bi1,Bi2,…,Bis}。通过FAHP方法确定权重,准确评估用能水平。

2.2.2 模糊互补判断矩阵的构造

通过采用一致矩阵法,FAHP确定了各个子指标的相对权重。该方法通过各指标之间的比较,利用相对尺度降低了对不同指标之间比较的困难。逐层计算指标元素的相对重要性,并构建模糊互补判断矩阵。

(1)

公式中:mij为指标因素Bi与指标因素Bj对比的相对重要性。根据参考文献[16],给出了不同相对重要程度下矩阵元素的取值标准如表1所示。

表1 判断矩阵取值标准Tab.1 Judgement matrix value criteria

2.2.3 一致性测试与调整

逻辑一致性确保了一致性指标权重的准确性,以确保对指标重要性的判断没有矛盾。在文中,使用指数γ值的大小作为判断矩阵一致性程度的依据。γ的值越大,则一致性越差[16]。指数γ的计算为

(2)

2.2.4 一致性测试与调整的流程

1)设阈值σ并且与γ指数进行比较,若σ小于指数γ则需要调整矩阵M;

2)建立权重判断矩阵

(3)

3)计算M和M(k)之间的关联程度:

(4)

4)根据最小值原理a(k1)=min{a(1),a(2),…,a(n)},确定加性一致性矩阵Mk1,该矩阵与模糊互补矩阵M最接近,并表示为M*;

5)计算偏差矩阵Q=(qij)n×n:

(5)

6)根据偏差矩阵Q的结果,调整判断矩阵M的一致性。若bst>0,则令M′st=Mst-λ,M′ts=Mts+λ;反之令M′st=Mst+λ,M′ts=Mts-λ。调整系数λ取值为0.05。将调整后的矩阵M′作为新的模糊互补判断矩阵M,并返回到步骤1进行下一轮计算。

2.2.5 单层指标排序

单层指标排序是根据本层各指标的重要性对其进行排序,计算出权重向量w。

1)求和:将判断矩阵M的每一行相加

(6)

2)计算单层指标的权重向量W=(w1,w2,…,wn)T,权重向量W中的元素wi为

wi=(ai+0.5n-1)/n(n-1);

(7)

通过以上步骤,可以得到本层次指标的权重向量wi,用于衡量各个指标的重要性。

2.2.6 多层指标总排序

多层指标总排序是指对评价系统中所有子指标相对于目标层的重要程度进行综合权重计算。通过逐层比较和权重推导的过程,从顶层到底层逐步确定每个指标在整个评价体系中的重要性,最终得到每个指标的权重向量。从顶层到底层的权重向量为

W(s)=W(s)W(s-1),…,W(3)W(1)

(8)

根据专家经验,我们构建了多层用户用能综合评价指标体系的模糊互补判断矩阵,并利用Matlab成功计算了子指标的权重信息。然而,FAHP方法在评估指标相对重要性时只考虑了优劣关系,未考虑具体情况的重要性程度。因此,对于比较不同指标的绝对重要性,需要采用CRITIC方法。

2.3 客观权重计算—CRITIC法

CRITIC法是一种能够确定指标客观权重的方法,它综合了指标内部变异大小和指标间的冲突性来确定权重[17]。通过综合这两个方面的因素,CRITIC法可以有效地确定指标的客观权重,从而提高决策结果的准确性。

1)原始数据无量纲化处理。对原始数据按公式(9)、公式(10)进行处理。

正向指标:

xij=[x′ij-min(xj)]/[max(xj)-min(xj)]

(9)

逆向指标:

xij=[max(xj)-x′ij]/[max(xj)-min(xj)]

(10)

公式中:xij为标准化值;x′ij为变量j的初始值;max(xj)为指标j的最大值;min(xj)指标j的最小值。

2)单独考虑每个指标生成的向量,得到标准差向量σj。

(11)

3)计算两个指标之间的线性相关系数Rij。

Rij=cov(x′i,x′j)/(σi,σj),i、j=1,2,…,n

(12)

公式中:Rij为指标i与指标j的相关系数;δi为指标i的标准差;δj为指标j的标准差;n为指标数。

4)计算信息量。计算指标i包含的信息量Ci

(13)

5)根据公式(14)进行权重归一化处理。

(14)

2.4 指标综合权重的计算

FAHP法在一定程度上存在主观局限性,而CRITIC法则无法根据实际情况提供适合的主观偏向,且过于依赖原始数据,具有较大的客观局限性。因此,在这种情况下,需要进行组合赋权的方法。为了使指标的综合权重尽可能的接近主观权重与客观权重,不偏向任意一项,使用FAHP-CRITIC法确定指标的综合权重为

ω综合=βω主观+(1-β)ω客观

(15)

公式中:β为相对重要程度参数,范围在0-1之间。在经过专家咨询后,确定β值为0.618。使用FAHP方法计算指标的主观权重,并使用CRITIC方法计算指标的客观权重,然后应用公式(15)计算各个指标的综合权重。

3 算例分析

为了验证本文方法的适用性与可靠性,选取东北某典型工业园区4家不同行业大工业用户用电数据,不同工业用户的基本信息如表2所示。在Matlab R2018b环境下,以内存为16GB和Inter i5处理器的PC为平台进行仿真分析。以清洁能源占比L21、减排率L22、余能利用率L23、电能替代水平L24以及废气达标水平L25,5个二级指标为例,利用FAHP-CRITIC算法计算各指标的主观权重、客观权重、综合权重等参数,进而计算不同行业工业用户用能特性的各评价指标的综合权重,最终得到不同行业工业用户的用能特性画像。基于FAHP-CRITIC综合权重计算法刻画不同行业工业用户的用能特性画像流程如图2所示。

表2 不同行业工业用户基本信息Tab.2 Basic information of industrial users in different industries

图2 FAHP-CRITIC综合权重计算法流程图Fig.2 Flow hart of FAHP-CRITIC comprehensive weight calculation method

3.1 基于FAHP的主观权重

根据表1中的判断矩阵取值标准询问相关专家的意见,对二级指标L21—L25进行两两比较,构造模糊判断矩阵ML2:

一致性检验。将一致性指数设定阈值预设为0.01,利用公式(2)计算模糊判断矩阵ML2的检验系数δ=0.0833。由于δ>λ,需要进行一致性调整。利用公式(3)～公式(5)计算偏差矩阵QL2对判断矩阵ML2进行调整,在调整9次后,得到检验系数小于一致性指数设定阈值的判断矩阵M′L2为

根据公式(6)与公式(7)计算二级指标L21～L25对低碳用能指标的主观权重值:αL21=0.232 5、αL22=0.215 0、αL23=0.180 0、αL24=0.217 5、αL22=0.155 0。

3.2 基于CRITIC的客观权重

指标L21～L25的原始数据如表3所示,指标原始数据的计算方法包括邀请4位专家评分、统计相关数据以及查阅相关标准。根据公式(9)～公式(10)对原始数据进行无量纲化处理,得到标准化矩阵S:

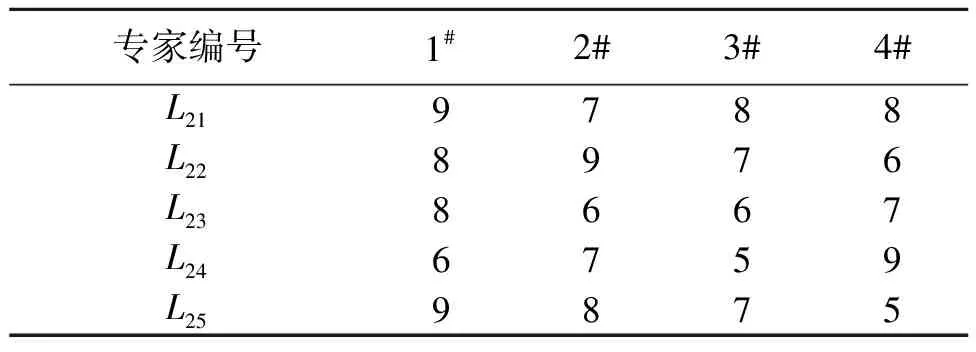
表3 低碳用能二级指标的评分结果

计算标准化矩阵S各行向量的标准差,利用公式(12)计算各个指标之间的相关系数,得到相关矩阵R:

利用公式(13)计算各指标包含的信息量:μ21=1.416 4、μ22=1.723 0、μ23=1.377 8、μ24=1.623 5、μ25=0.123 2。由公式(14)得到客观权重值:β21=0.202 2、β22=0.246 0、β23=0.196 7、β24=0.231 8、β24=0.123 2。

3.3 基于组合赋权的综合权重

利用公式(15)计算清洁能源占比L21、减排率L22、余能利用率L23、电能替代水平L24以及废气达标率L25等指标的综合权重值,结果如表4所示:

表4 基于FAHP-CRITIC的综合权重Tab.4 FAHP-CRITIC based composite weights

基于上述方法,计算出各用户用能特性评价指标的综合权重,以及其他用户各用能特性评价指标的综合权重。具体结果请见图3

图3 各用户综合权重系数对比图Fig.3 Comparison chart of comprehensive weight coefficient of each user

3.4 用户用能评价主观权重、客观权重、综合和权重计算结果对比分析

为了提高服务质量并保持市场竞争力,电力企业需要更为深入地掌握各行业的用电规律。本文通过对主观权重和客观权重的详细分析,揭示了不同行业在多元用户用能行为上的特点和差异。计算结果见图4、图5。

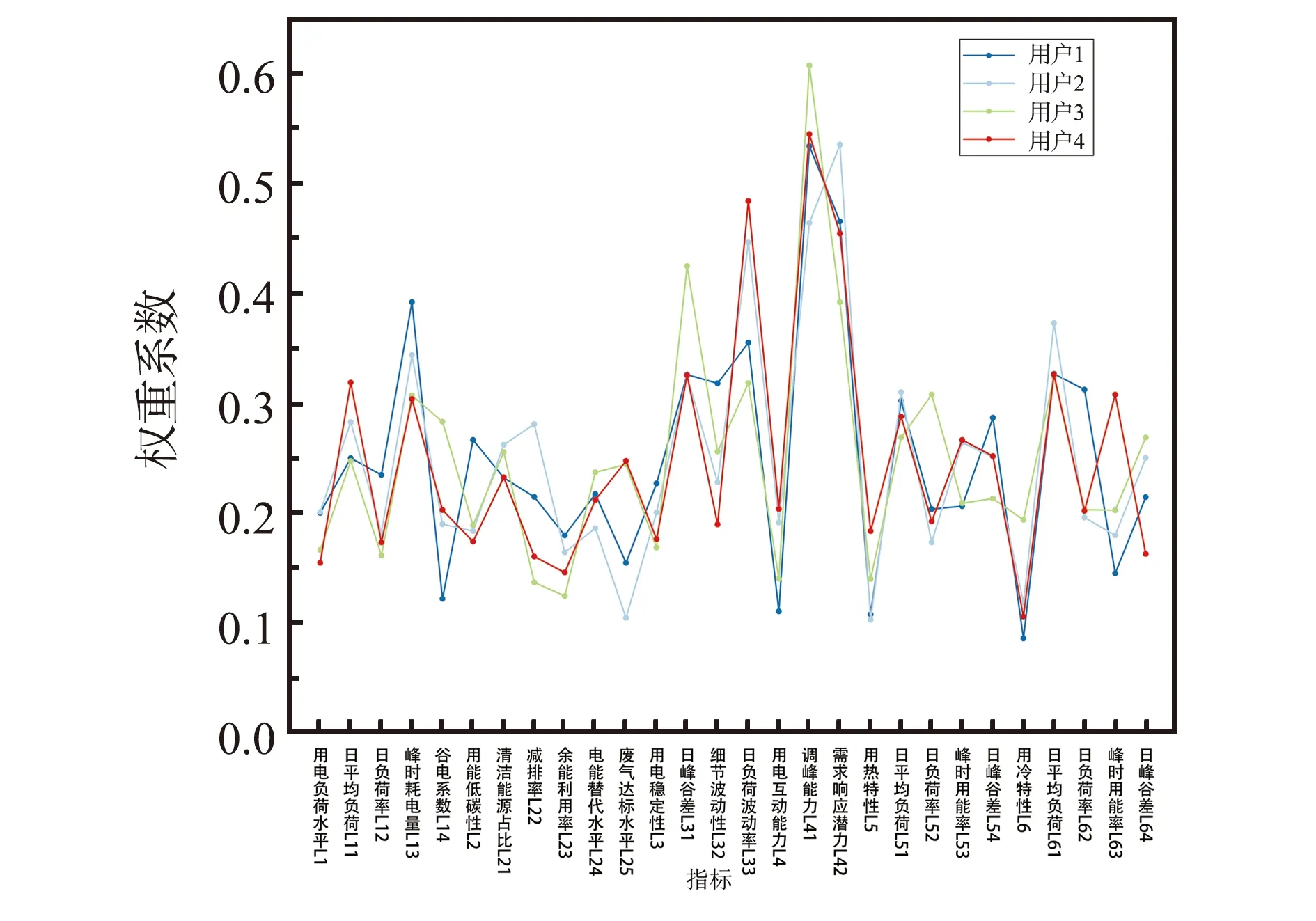
图4 各用户主观权重系数对比图Fig.4 Comparison chart of subjective weight coefficient of each user

图5 各用户客观权重系数对比图Fig.5 Comparison chart of objective weight coefficient of each user

结合图3、图4、图5,在电子制造业(用户1)中,峰时耗电量L13的主观权重达到了0.392 3,显示出较高的电力需求,但其客观权重为0.233 7,表明实际需求略低。通过综合权重0.331 7,用户1可以得到了更为准确地反映该行业真实需求的权重。对于汽车制造业(用户2),其日负荷波动率L33的主观权重为0.446 5,表明其对电力需求的不均匀性关注,但客观权重稍微低一些,为0.384 5。然而,综合权重0.422 8为用户2提供了一个全面的视角,准确地揭示了这一行业的电力需求。在金属加工机械制造业(用户3)中,其调峰能力L41的主观权重为0.607 7,显示了较高的需求,但客观数据稍低,为0.523 9。这种差异通过综合权重0.575 7得到了平衡,从而更真实地展现了该行业的需求。化学材料制造业(用户4)对于日负荷的稳定性有高度关注,这从其日负荷波动率L33的主观权重0.484 3就可以看出,但客观权重为0.353 9,与主观权重存在差异。最终,综合权重0.434 5全面地揭示了该行业在生产中的日负荷稳定需求。由此可见,使用的FAHP-CRITIC综合权重计算法与传统的仅基于主观或客观权重的计算方法相比,具有明显优势。它结合了两者的优点,既能反映用户的偏好,也能与实际情况相符,避免了仅依赖单一视角可能出现的偏见和误差。更重要的是,FAHP-CRITIC方法提供了一个更全面、更深入的视角,使得用能行为特性的分析更为准确和细致。

综上所述,各行业虽然在多数电能使用指标上的主观和客观权重都相差不大,但在某些关键指标上确实存在差异。这些差异揭示了不同行业在多元用户用能中的特定需求和偏好,为多元用户制定更为精准的能源策略提供参考。同时,本文提出的FAHP-CRITIC方法也为工业用户提供了一个深入而详细的工业用户用能行为分析工具。随着新型电力系统和电力市场的进一步发展,这种深入了解和分析将为工业用户提供更为强大的决策支持,帮助其更好地应对未来的挑战。

3.5 不同行业工业用户用能特性画像分析

为比较不同行业工业用户的用能特性,本文将用户用能特性各评价指标的权重作为多维度指数,形成不同用户的用能特性画像如图6所示。

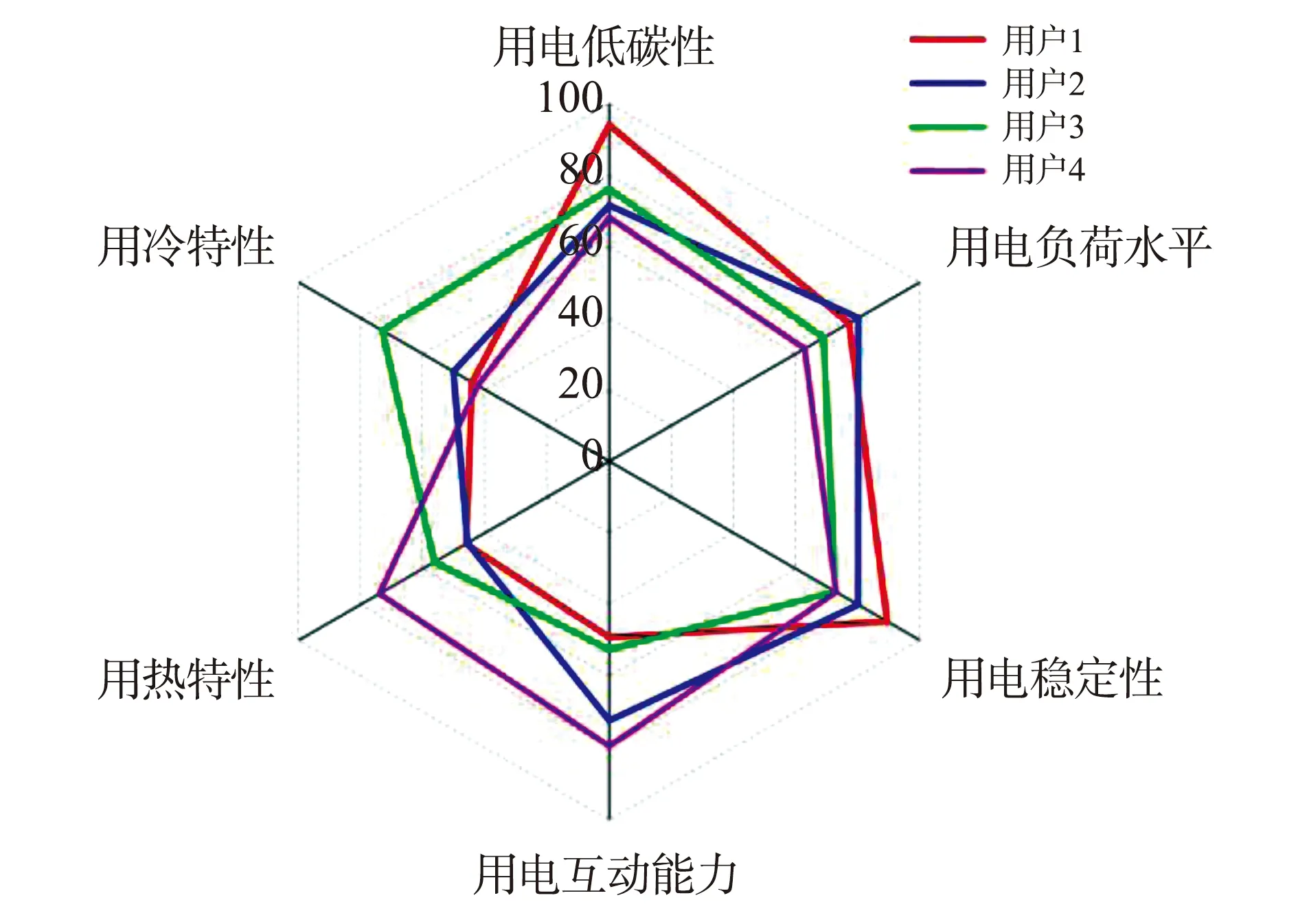
图6 不同行业工业用户用能特性画像Fig.6 Profiling the energy use of industrial users in different sectors

从图6中可以看出,大部分的工业用户注重用能的低碳型与稳定性,其中,用户1在低碳用能与用电稳定性方面的指数高于其他用户。但是在用电互动能力方面,用户1的指数最低,这是因为用户用能越稳定,其负荷曲线越平缓,可转移的负荷越少,进而导致用户的用电互动能力越弱。从图6中还可以看出,用户3在用冷特性方面表现的最好,用户4在用热特性方面表现的最好。此外,根据行业用能画像的结果,电力公司可以按照用户在不同用能特性方面的表现为用户提供个性化的用能服务。

根据不同行业用能特性评价指标的综合权重与用能画像,计算各行业的综合用能得分(百分制),如图7所示。从图7中可以看出,用户1的综合用能得分最高,用户4的综合用能得分最低,其余用户的综合得分介于用户1、2之间。其中,用户1的综合用能得分达到76.676,这是因为用户1在用能低碳性与用能稳定性两方面相对于其他用户具有突出的评分表现。此外,用户可以依据综合用能画像与得分提出用能改进方向,如用户4,尽管在用热特性与用电互动能力方面指标评分较高,但其综合用能得分最低,因此需要加强用能的低碳性与稳定性。

图7 不同行业工业用户综合用能得分Fig.7 Comprehensive energy use scores for industrial users in different sectors

4 结 论

本文提出一种基于改进的AHP-CRITIC综合权重计算的多元用户用能行为特性画像及评价方法。在考虑指标的可获取性的前提下,该方法从用电负荷水平、用电低碳性、用电稳定性、用电互动能力和用热/冷特性六个指标对用户用能水平进行分层评估。同时,构建含有低碳用电指标的用户综合用能评价体系,运用主观与客观权重计算法相结合的综合权重计算法得出指标权重,进而确定工业用户用能指标权重,生成考虑多元用户用能特性的工业用户用能行为特征画像。该方法着重体现工业用户对不同能源的消费特点,同时可以分析工业用户用能特征。算例分析结果表明,本文提出的方法能够深度挖掘用户用电特征,并且生成实用性较强的用户用电行为画像,为各工业用户在用能方面提供意见与改进方案。