振动能量收集系统的输出功率优化设计与分析

许冠华,赵新龙

(浙江理工大学信息科学与工程学院,浙江 杭州 310018)

振动能量收集技术是将自然界中的或人为产生的机械振动能转换成可用的电能的过程,常用的技术有电磁式、静电式与压电式[1-4]。其中,压电式振动能量收集技术具有比其他二者更大的能量密度[5],兼有绿色无污染、结构简单等特点[6-7]。近年来,无线传感器网络对小规模、便携式和可再生能源提出了更大的需求[8-10],研究人员们期望用压电振动能量收集技术来取代日渐暴露出更多问题的传统电化学电池[11-12],以延长无线传感器的使用寿命[13]。如何进一步提升用来俘获振动能量的压电能量收集器(Piezoelectric Energy Harvester,PEH)的机电转换效率,成为了一个亟待研究人员们解决的问题。

为了提升PEH的转换效率,Shad Roundy等[14]发现当悬臂梁的形状由矩形向三角形靠拢时,悬臂梁轴向的应力分布会更加均匀,但由于三角形悬臂梁末端无法连接质量块,故提出利用梯形悬臂梁来代替传统矩形悬臂梁以提升能量转换效率。Hai Wang等[15]设计了一个具有六段折叠梯形梁结构的PEH,该结构具有更低的谐振频率和距离更近的谐振峰,从而具有更好的电学输出特性,但该PEH的体积太大,不适合用于微小无线传感器中,且当振动频率大时,各段梯形梁容易发生碰撞。Pradeesh等[6]则探究了压电材料与质量块在悬臂梁上不同的放置方式与放置位置对PEH输出特性的影响,结果表明在质量块的质量不变时,质量块的材料与体积对PEH的输出功率与谐振频率无显著影响。还有很多学者期望改变悬臂梁的几何结构来改善PEH的输出特性,Annapureddy Rami Reddy等[16]设计了一种带有梯形空腔的悬臂梁,实验表明该结构的输出电压比带有矩形空腔的和无空腔的悬臂梁的输出电压分别增加了97.5%和108%,但该种梁制作工艺比较复杂,成本较高。Zhongjie Li等[13]在PEH的矩形悬臂梁中引入了旋转关节,通过有限元分析和实验发现,嵌入旋转关节可降低PEH的刚度,使谐振频率降低,使输出电压提升了2.83倍,但该PEH选用的是传统的矩形悬臂梁,应力分布不均,没有使输出最大化。

综合以上研究中出现的问题,为了进一步优化电学输出特性,本文提出了一种在梯形悬臂梁的自由端进行切口的方案,利用COMSOL Multiphysics进行有限元仿真,研究带有特定形状切口的PEH的谐振频率、悬臂梁末端位移、输出电压频率响应、最大输出功率和最优负载,研究当PEH具有特定形状切口时,能否改善其电学输出特性。

1 结构理论分析

梯形悬臂梁的俯视图如图1所示。假设弹性支撑梁的厚度为2a,杨氏模量为Eb,压电层的厚度为b,杨氏模量为Ep,梁长为L,固定端的宽度为ws,自由端的宽度为wf,沿梁伸长方向x距离处的梯形悬臂梁的宽度为wx,则wx可表示为

图1 梯形悬臂梁结构示意图Fig.1 Schematic diagram of trapezoidalcantilever beam structure

(1)

根据牛顿第二运动定律,建立如图2所示的基于振动梯形梁的集总参数理论模型。

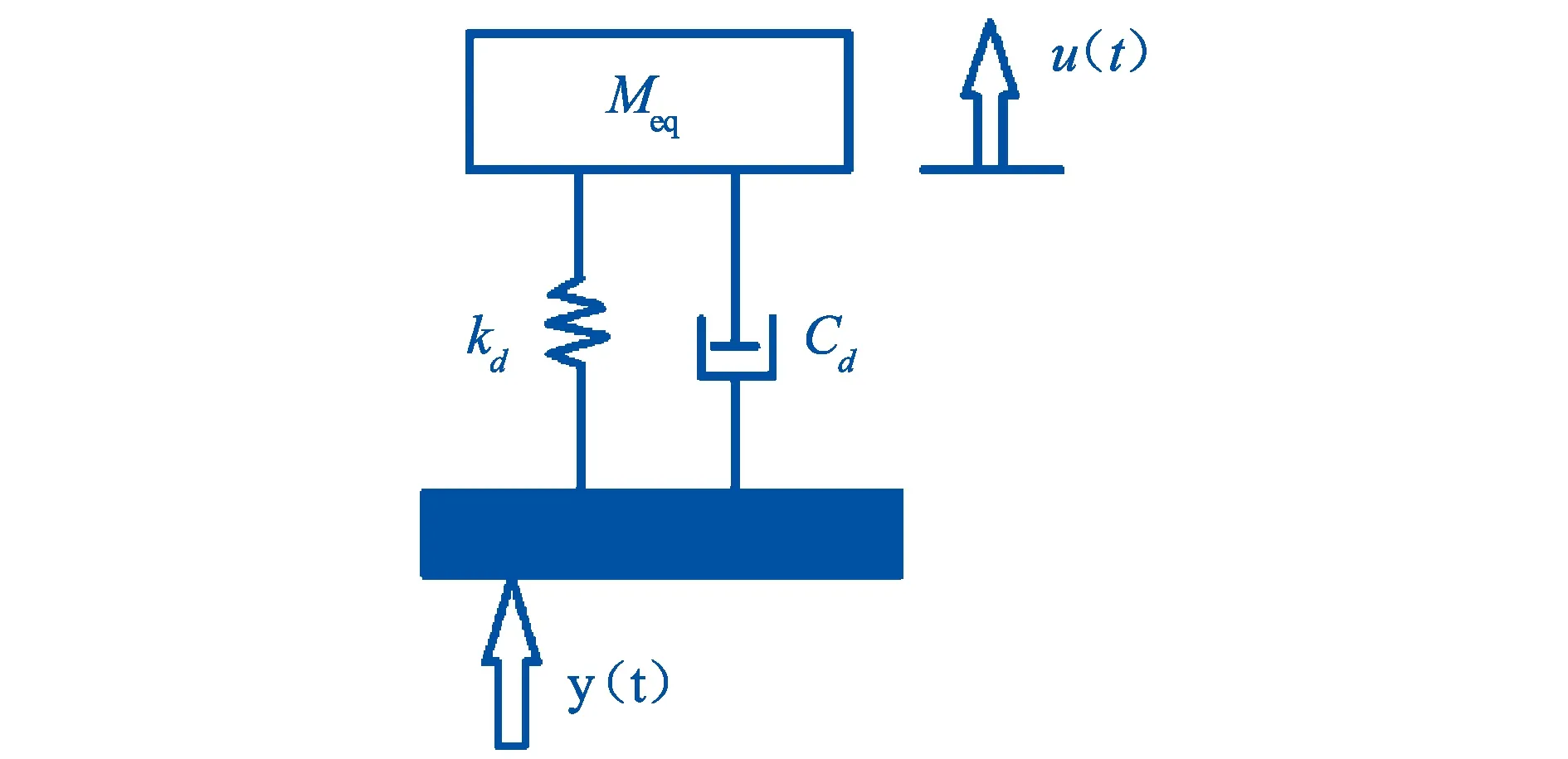
图2 基于振动梯形梁的集总参数理论模型Fig.2 Theoretical model of lumped parameters based on vibrating trapezoidal beam

描述系统运动的微分方程为

(2)

公式中:y(t)为外界输入的振动信号;u(t)为质量块的位移;Meq为等效质量;Cd为压电梁的阻尼系数;kd为等效弹簧的弹性系数。等式两端同时作拉普拉斯变换得到

s2MeqU(s)+sCdU(s)+kdU(s)=Y(s)

(3)

则等效系统的传递函数为

(4)

系统的固有频率亦即特征频率为

(5)

公式(5)说明可以通过改变等效质量的大小来改变系统的固有频率,使其更接近于环境振动频率。系统的阻尼因子为

(6)

对整个悬臂梁-质量块系统进行力学分析,可以得到结构的固有频率为

(7)

在加速度a(t)下,支撑梁和质量块的交界点沿z轴方向的位移为[17]

(8)

结合材料力学的知识可以得到支撑梁上的最大应力σmax发生在固定端处,且最大应力为

(9)

2 新型结构设计

将固定端长度为20 mm,自由端长度为8 mm,长度为20 mm,厚度为0.2 mm的等腰梯形梁记为0#梁。本文提出了一种在0#梁自由端作特定形状切口的方案,该切口在0#梁自由端的中心位置,切口尺寸为3.2 mm×5 mm,面积为16 mm2,将带有切口的梁记为1#梁。之后在0#梁和1#梁固定端中心位置的上表面粘结一片长p=8 mm,宽q=4 mm,高b=0.1 mm的压电陶瓷,并设其杨氏模量为Ep。0#梁和1#梁各处的具体尺寸如图3所示。

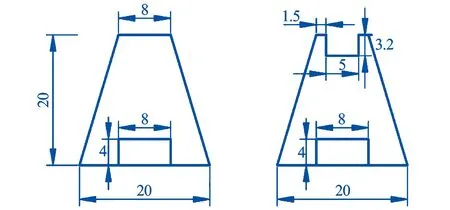
图3 0#梁和1#梁的示意图Fig.3 Schematic diagram of 0# and 1# beams

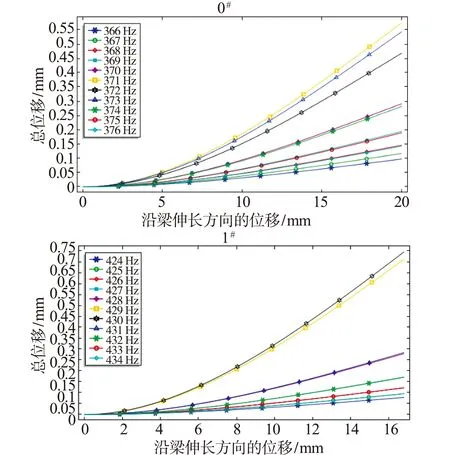
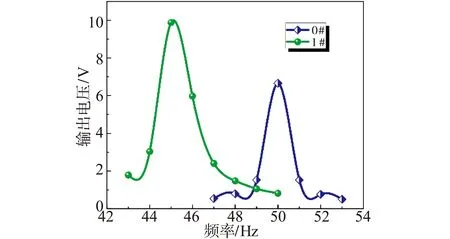
0#单晶压电悬臂梁在沿梁的伸长方向上按横截面的类型不同总共可以被分成2段:第一段,0

当0

(10)

第一段的惯性矩I1可以表示为

(11)

当q≤x

(12)

故对于固定端贴有压电陶瓷的0#梁,惯性矩方程为

(13)

当0

(14)

压电陶瓷区域下悬臂梁的应力

(15)

取

σ1(x)=max{σ1,1(x),σ1,2(x)}

(16)

则应变

(17)

其中,若σ1,1(x)>σ1,2(x),则取i=p;若σ1,1(x)<σ1,2(x),则取i=b。

当q≤x

(18)

即对于固定端贴有压电陶瓷的0#梁,其应变方程可写为

(19)

1#单晶压电悬臂梁在沿梁的伸长方向上按横截面的类型不同总共可以被分成3段:第一段,0

(20)

(21)

众所周知,PEH产生的输出电压与其应变成正比[18]。整个系统的输出电压[19]可表示为

(22)

公式中:ω为振动圆频率;t为时间;φ为相位差;ε33为介电常数;N为常数。当给定PEH一正弦激励y(t)=Asinωt时,悬臂梁末端的质量块会发生振动,压电材料的输出功率Pd为[20]

(23)

为了将输出功率最大化,驱动PEH的正弦激励的频率ω应该和系统的固有频率ωn相匹配,即最大输出功率发生在ω=ωn时,此时有

(24)

3 有限元仿真分析

利用有限元仿真软件COMSOL Multiphysics对PEH进行仿真。设置弹性支撑梁的材料为铜,压电材料为PZT-5H(锆钛酸铅压电陶瓷),质量块的材料为PMMA(亚克力),相关零部件的尺寸和部分性能参数如表1所示。采用映射法和扫掠法进行网格划分,将压电陶瓷下表面的电势置零。

表1 各部件尺寸和性能参数

0#PEH和1#PEH的前三阶谐振频率如表2所示。结果表明,在梯形梁自由端切口的方案可以降低PEH的谐振频率,使其能更好地工作在低频振动的环境中。从表中还可以得出,两种PEH的前二阶谐振频率数值相差较大,这使得它们可以工作在某个低频振动环境中而不受自身谐振频率特性的干扰。

表2 0#PEH和1#PEH的前三阶谐振频率(Hz)

为0#PEH和1#PEH施加沿z轴方向上的加速度大小为1 g的正弦激励,在各自一阶谐振频率±5 Hz的范围内研究沿梁伸长方向上各点的位移情况。选取梁上表面中轴线为路径,可以绘制出如图4所示的梯形梁中轴线上所有点的位移图。从图4中可以得出,0#梁和1#梁的最优位移曲线都发生在各自的一阶谐振频率处,各梁的最大位移都发生在梁的自由端。其中,0#梁的最大末端位移为0.58 mm,1#梁的最大末端位移为0.75 mm,较0#梁提升了29.3%。

图4 0#梁和1#梁沿轴向的位移图Fig.4 Displacement diagrams of 0# beams and 1# beams along the axial direction

在各模型的一阶谐振频率处研究加速度相关性,设定加速度的变化范围为0.25～2 g,在此过程中计算各模型的输出电压与输出功率,其结果如图5所示。从图5中可以看出,输出电压和输出功率都与加速度呈正相关,其中输出电压与加速度之间还是线性增加的关系。

图5 0#PEH和1#PEH在一阶谐振频率下的加速度相关性Fig.5 Acceleration correlation of 0# PEH and 1# PEH at the first resonant frequency

为整个PEH施加一个沿z轴方向的加速度大小为0.5 g的正弦激励,在各PEH的一阶谐振频率±5 Hz的范围内研究其输出电压的频率响应,结果如图6所示。从图6中可知,0#PEH和1#PEH的输出电压峰值都出现在其各自的一阶谐振频率处,1#PEH的最大输出电压为9.88 V,比0#PEH的输出电压增长了48.3%。

图6 0#PEH和1#PEH的输出电压频率响应曲线Fig.6 Output voltage frequency response curves of 0# PEH and 1# PEH

在各模型的一阶谐振频率处研究负载相关性,设定负载电阻的变化范围为1 kΩ到100 MΩ,在此过程中计算各模型负载电阻两端电压和输出功率,其结果如图7所示。结果表明,随着负载电阻的增大,负载两端电压整体呈现增大的趋势,值得注意的是,负载电压曲线的斜率从0开始增大,随后又逐渐变成0,最终趋于一个稳定的电压值。而输出功率曲线整体先增大后减小,在波峰两侧,功率曲线呈对称分布。随负载电阻的增大或减小,输出功率都将趋向于零,这与电路分析中的相关理论所得到的结论是一致的。其中,0#PEH和1#PEH的最大输出功率分别为6.23 μW和9.46 μW,1#PEH的最大输出功率较无切口的0#PEH提升了51.8%。因此,由阻抗匹配理论知,1#PEH的最优化阻抗约为2.2 MΩ,即该种情况下系统的最佳负载为2.2 MΩ。综上分析,可以确定在梯形悬臂梁自由端作特定形状切口可以有效改善PEH的电学输出特性。

图7 0#PEH和1#PEH在一阶谐振频率下的负载相关性Fig.7 Load correlation of 0# PEH and 1# PEH at the first resonant frequency

4 结 论

本文通过理论模型分析和COMSOL Multiphysics有限元仿真方法分析了一种在梯形悬臂梁自由端作特定形状切口的方案,得到了其模态分析、挠度分析、输出电压频率响应、最大输出功率和最优负载。分析结果表明,在梯形悬臂梁自由端作1#切口的方案可以提升PEH的电学输出特性,在该种切口条件下:一阶谐振频率较不切口时降低了10.3%,使其能更好地工作在低频振动环境中;当外界正弦激励的频率为45 Hz,加速度为0.5 g时,1#PEH的最大输出功率达到9.46 μW,比无切口的压电能量收集器提升了51.8%。