音圈直线电机滑模变结构控制方法

张鑫宇,吴忠实,周淼磊

(吉林大学通信工程学院,吉林 长春 130022)

0 引 言

音圈直线电机是一种典型的永磁电机执行器,其输出力的大小由通电导体的电流大小决定,受力方向由通电导体的电流方向决定[1]。音圈直线电机具有纳米级的定位精度,结构相对简单,并且其工作时不需要柔性铰链等复杂的装置进行传动,因此广泛应用于小行程、高频率和高精度的重复定位领域[2-5]。但是其本身存在着非线性特性,这一特性对其定位精度产生了严重影响[6]。

为了消除非线性特性对音圈直线电机定位精度的影响,实现高精度定位控制,研究人员对其进行了大量的研究。电子科技大学的高椿明[7]等提出了一种基于扰动观测器(DOB)的H∞控制方法,实验结果表明提出的控制方法增强了系统的鲁棒性。张武军等[8]设计了一种结合模糊预测补偿器的PID控制方法,并将该算法应用在一自由度音圈直线电机上,实验结果表明提出的控制算法可将误差控制在15 μm的以内。台湾淡江大学许春飞等[9]使用PD控制并结合自学习模糊逻辑控制器,设计了一种复合控制方法,实验结果表明所提出的混合控制器在音圈直线电机载荷发生变化时也具有良好的跟踪性能。陈子印等[10]针对具有参数不确定性的音圈电机驱动的指向镜系统,设计了一种自适应动态面控制方法,为了减小滤波误差,基于系统的跟踪误差构建了补偿环节,仿真结果证明了所设计控制器的有效性。文献[11]中将扩张状态观测器和积分器与传统的复合非线性反馈控制相结合,提出了一种改进的复合非线性反馈控制方法,实验结果表明所提出的控制方法提高了系统的稳态精度和抗扰性能。北京航空航天大学张立佳等[13]基于BP神经网络提出了一种可以在线整定参数的神经网络PID控制器,并应用在音圈电机直驱阀上,仿真结果表明所提出的控制方法具有良好的控制性能。华东交通大学高莹[13]将径向基神经网络自抗扰控制应用到音圈电机中速度控制中,实现了自抗扰控制器参数的自适应调节。研究结果表明,相比于PID控制,提出的径向基神经网络自抗扰控制有效提高了系统的鲁棒性和响应速度。文献[14]提出一种模型参考自适应控制器,进一步提高了系统控制精度,并降低了控制器设计过程中对于系统模型的依赖。文献[15]提出一种将有限时间控制与自适应滑模控制相结合的鲁棒有限时间自适应控制器(FAC),同传统的滑模控制相比跟踪精度提高了19.8%。上述对音圈直线电机设计的控制策略均能取得良好的控制效果,但未从物理特性的角度考虑影响音圈直线电机定位精度的非线性因素。

因此,本文依据音圈直线电机的物理特性,根据牛顿第二定律推导音圈直线电机的机理模型,并采用最小二乘方法对其参数进行辨识。为了提高音圈直线电机的定位精度,通过摩擦力测试得到了音圈直线电机系统的等效非线性项参数,设计了一种含有等效非线性控制项的滑模变结构控制器以补偿音圈直线电机的非线性摩擦特性。最后通过实验验证了本文所提出控制方法的有效性。

1 音圈直线电机模型

为了建立音圈直线电机的模型以及设计有效的控制方法,本节首先对音圈直线电机的非线性摩擦特性进行测试,得到输入信号与摩擦力的关系。然后,运用牛顿第二定律推导音圈直线电机的机理模型,最后采用最小二乘法[16-17]对模型未知参数进行辨识。

1.1 音圈直线电机摩擦测试

摩擦力测试的方法为:输入的电流信号为正弦形式,位置信号的具体数值可由光栅测量得到,对得到的数据进行求导可以得到音圈电机运动的速度。通过Copley驱动器驱动音圈直线电机进行测试,摩擦力测试结果如图1所示:图中记录了输入电流和输出速度随时间变化的值。

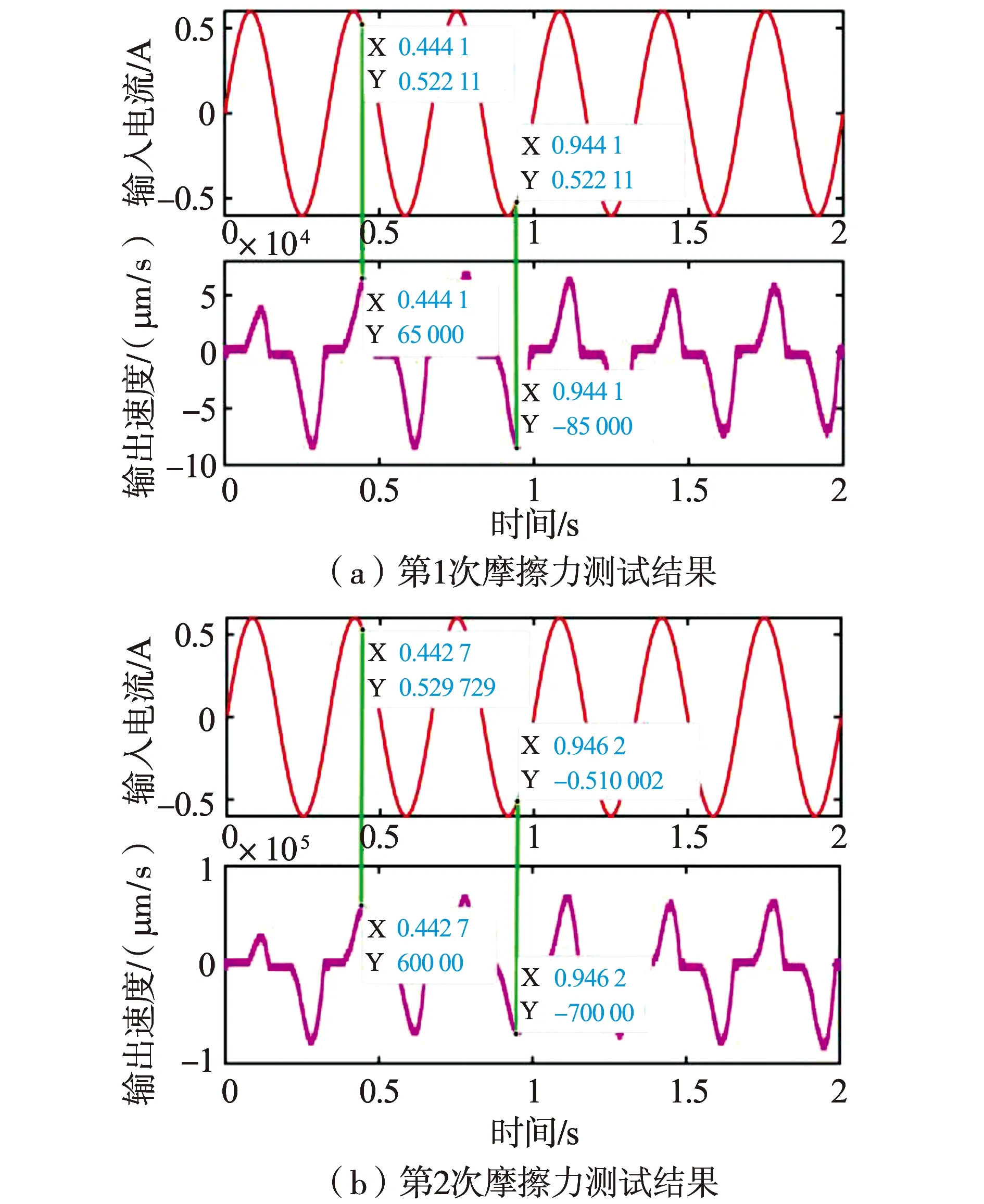
图1 音圈直线电机摩擦力测试图Fig.1 Voice coil linear motor friction test diagram

图1为两次摩擦力的测试结果。由图1可知此时电流指令最大约为0.53 A。通过电流的大小可以间接推导出摩擦力的值,根据牛顿第二定律可得音圈直线电机的非线性摩擦为有界值。

1.2 音圈直线电机机理模型

音圈直线电机是一类典型的电磁执行器,其原理为线圈动子在永磁体中通电后,会受洛伦兹力作用并产生垂直于线圈平面方向的运动。因此,由牛顿第二定律和洛伦兹力方程可得动子在磁场中的受力和运动速度为

(1)

(2)

公式中:F为动子在磁场中受到的力;m为动子质量;x为动子位置;c为系统阻尼系数;v为动子的运动速度。

通过安培定律可得:

F=BiL=Kt·i

(3)

公式中:Kt为力常数;B为磁感应强度;i为通过线圈电流;L是在线圈的磁场内导线垂直于磁感线的长度。

结合公式(1)与公式(3)并进行拉普拉斯变换得到系统的传递函数G(s)为

(4)

公式中:X(s)为系统输出的位置信号;I(s)为系统输入的控制电流指令。

1.3 音圈直线电机模型最小二乘辨识

为更加全面的描述音圈直线电机系统的性能,选取的激励信号应使音圈直线电机的运动尽可能的遍布整个行程。采用表1所示的正弦信号激励音圈电机。

表1 输入信号幅值频率表Tab.1 Input Signal Amplitude and Frequency Table

忽略音圈直线电机的非线性影响,当输入为

Yu=Amsin(ωt)

(5)

输出为

Yy=Aysin(ωt+φ)

(6)

则有:

Yy=[sin(ωt)cos(ωt)][Aycos(φ)Aysin(φ)]

(7)

使用最小二乘方法辨识参数,令θ=[c1c2]T设计目标函数J(θ)如下:

J(θ)=(Yy-Ψθ)T(Yy-Ψθ)

(8)

对上式求导并令其导数为0,可得:

(9)

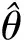
(10)

其中:

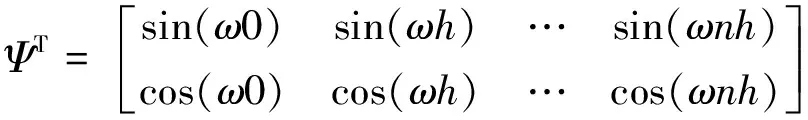
(11)

由此可得:

(12)

(13)

输入电流信号如公式(5)所示,当输入信号相移为0时,可以得到音圈直线电机系统的相频特性φe和幅频特性M的值,表达式为

(14)

(15)

其中:c1、c2的值由公式(10)得到,因此可通过上式得到φe和M的值。

2 音圈直线电机滑模变结构控制

由本文的建模部分可知:此音圈直线电机的传递函数模型部分为二阶系统,非线性特性主要表现为非线性摩擦,由摩擦力测试部分可知系统中存在的摩擦力是有界的并且可根据测试的最大输入电流计算得到。本文针对系统特性,设计一种滑模变结构控制方法,以达到精密定位这一控制目标。滑模变结构控制[18-19]是一种应用广泛的控制方法,常被用于微纳定位系统的控制。本文分别对系统的线性部分和非线性部分进行设计,即针对系统存在的非线性摩擦特性设计等效非线性控制项,对已建立的传递函数模型设计等效线性控制项。具体设计过程如下文所示。

2.1 音圈直线电机滑模变结构控制器设计

2.1.1 滑模变结构控制器等效线性项设计

由前文可知通过机理建模建立的音圈直线电机的传递函数模型如公式(4)所示。针对此模型进行控制器的等效线性控制项设计,控制原理图如图2所示:

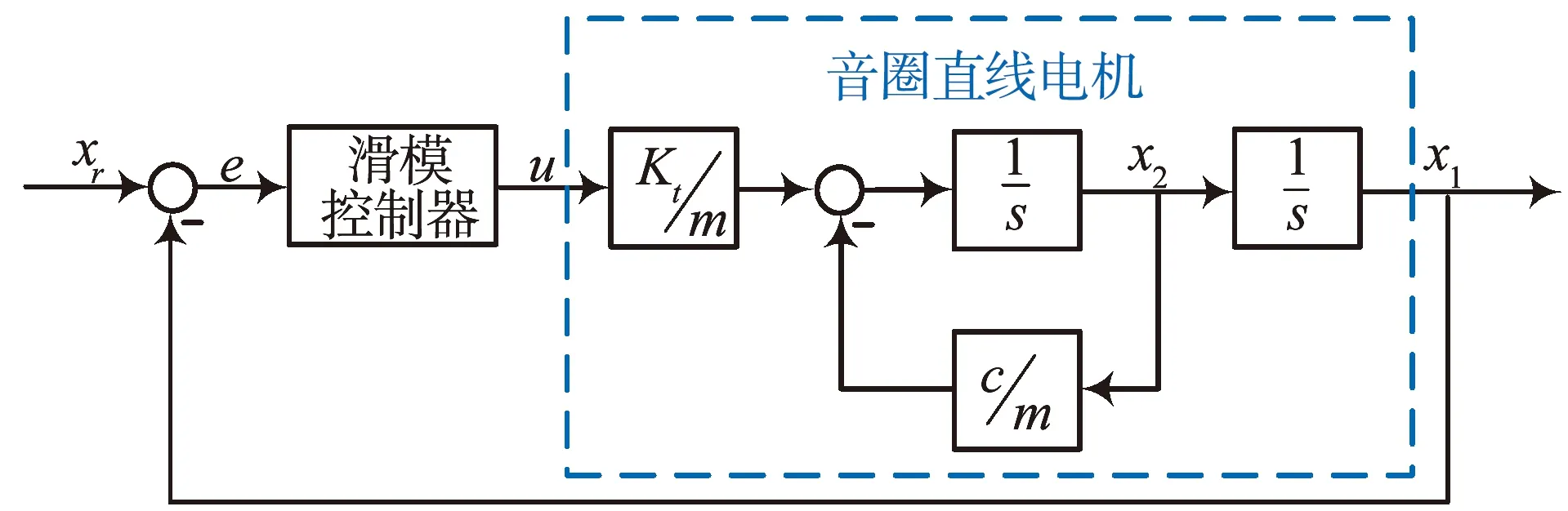
图2 音圈直线电机滑模控制原理图Fig.2 Sliding mode control block diagram for voice coil linear motor

将系统传递函数转换成状态空间方程为

(16)

公式中:x1为位置;x2为速度v;d为有界干扰。定义误差为

e=xr-x1

(17)

公式中:xr为期望输入信号。选取滑模面

(18)

公式中:k1、k2、k3分别为设计的正参数,对公式(18)求导后可得:

(19)

其中:

(20)

(21)

(22)

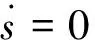
(23)

2.1.2 滑模变结构控制器等效非线性项设计

一般而言,滑模控制等效非线性项参数D的选取要大于外部干扰d才能抵消外界干扰对于系统稳定性的影响。音圈直线电机的主要非线性为摩擦力,根据牛顿第二定律有:

IKt-Cv-Ff=ma

(24)

公式中:Kt为力常数;C为阻尼系数;Ff为摩擦力;a为音圈直线电机的加速度。通过摩擦力测试可知,当速度信号在峰值处a=0,这时为静摩擦和滑动摩擦进行转换的时刻,Cv近似等于零,即IKt=Ff。由图1的测试可知输入信号的最大值为0.53 A,通过重复实验推得非线性摩擦为有界值,则可得外部干扰d为有界值。

设计等效非线性控制项为

(25)

因为当D的选取大于外部干扰d时,才能使得系统稳定,即(D/Kt)>0.53,下文将以实验说明此参数化方法具有实际工程意义。

在公式(23)上加等效非线性控制项usw可得:

(26)

公式中:k1、k2、k3,D分别为设计的正参数,sign(s)的表达式为

(27)

当系统趋近于切换面时,因为控制律中存在符号函数sign(s),这会使得系统随时间变化呈现出开关特性。该控制特性可以迫使系统沿规定的状态轨迹作小幅度、高频率的上下运动即会出现抖振问题。为了解决这一问题,本文选取合适的边界层系数,并使用饱和函数[20]替代符号函数来解决输出存在抖振的问题,控制律公式(26)变为

(28)

其中:

(29)

公式中:k为可调的边界层系数,当系统趋近于滑模面且s/k在正负1之间时,sat(s)为比例可导函数,使得滑模变结构的等效非线性控制项usw不会频繁的在正负之间切换,有效避免了系统产生不必要的高频振荡。

2.2 音圈直线电机滑模变结构控制稳定性分析

结合建立的线性模型和前文设计的控制律,进行稳定性分析,设计李亚普洛夫函数为

(30)

由上式可知,V>0对V求导有:

(31)

将公式(18),公式(19)带入上式得:

(32)

将公式(22)带入上式得:

(33)

把u带入公式(33)可得:

(34)

上式左侧为k3s,所以上式继续化简为

(35)

3 实验与分析

本节通过实验来验证所建立模型和设计控制器的有效性。实验使用PID控制来与本文提出的控制方法作对比。

3.1 音圈直线电机实验平台介绍

音圈直线电机实验平台原理图如图3所示,图4为音圈直线电机、驱动器以及电机控制器的实物照片图。该音圈直线电机的型号为:LC87-56-00A。驱动器为Copley驱动器,型号为:ACJ-055-09。

图3 音圈直线电机实验原理图Fig.3 Block diagram of voice coil linear motor experiment

图4 音圈直线电机实验平台Fig.4 Voice coil linear motor experimental platform

控制器为日本艾安得公司生产的AD5436。位置反馈选用高精度光栅尺,型号为MS15,除此之外,实验台还配备了高精度隔振台抑制外界环境干扰,型号为J02-1809。

3.2 最小二乘法辨识模型

利用最小二乘法对传递函数参数进行辨识,得到模型的传递函数如公式(36)所示。对得到的传递函数模型进行幅频与相频拟合实验,实验结果图如图5～图8所示:

图5 传函幅值实验与拟合图Fig.5 Transfer function amplitude experiment and fitted plot

图6 传函幅值误差图Fig.6 Transfer function amplitude error plot

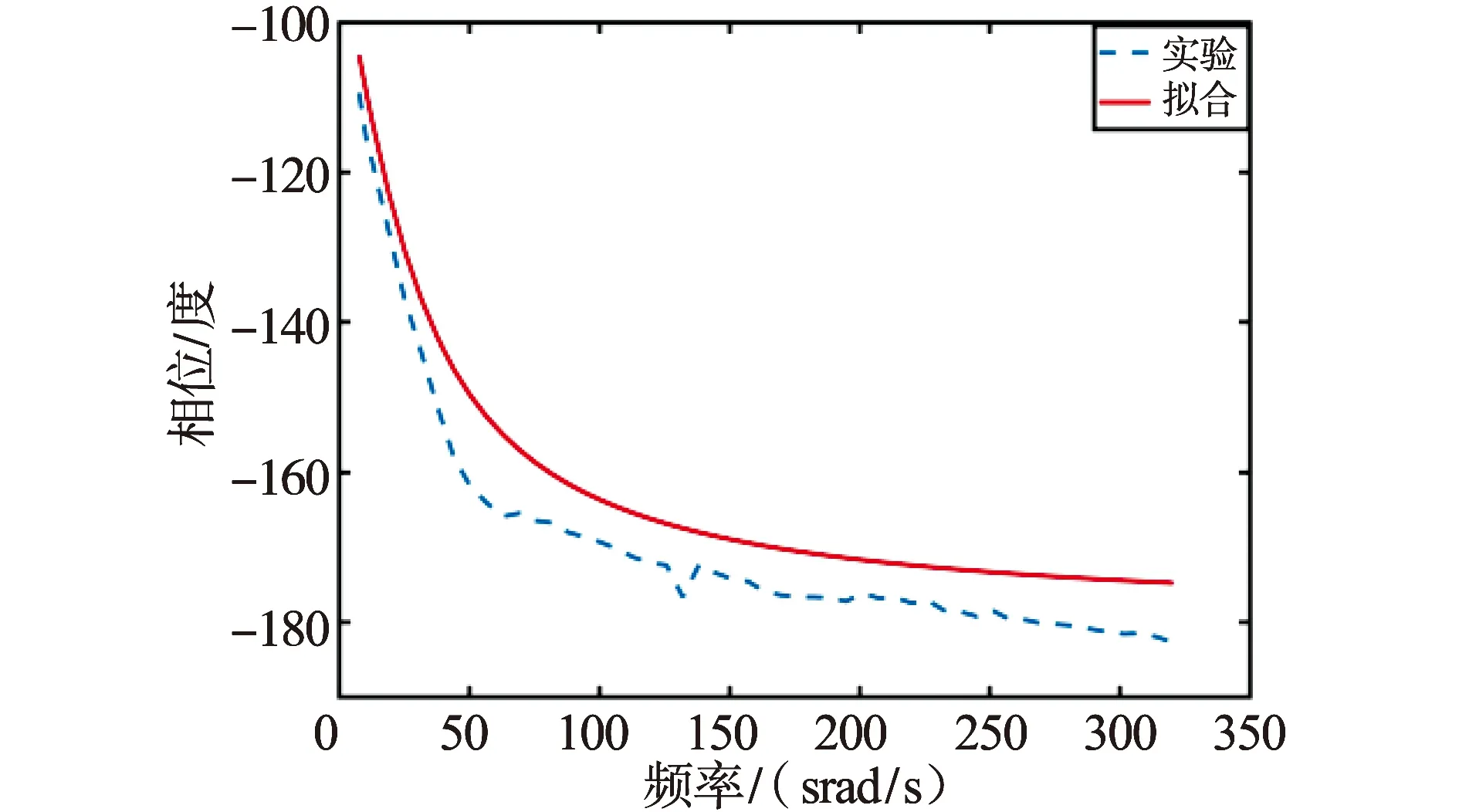
图7 传函相位实验与拟合图Fig.7 Transfer function phase experiment with fitted plot

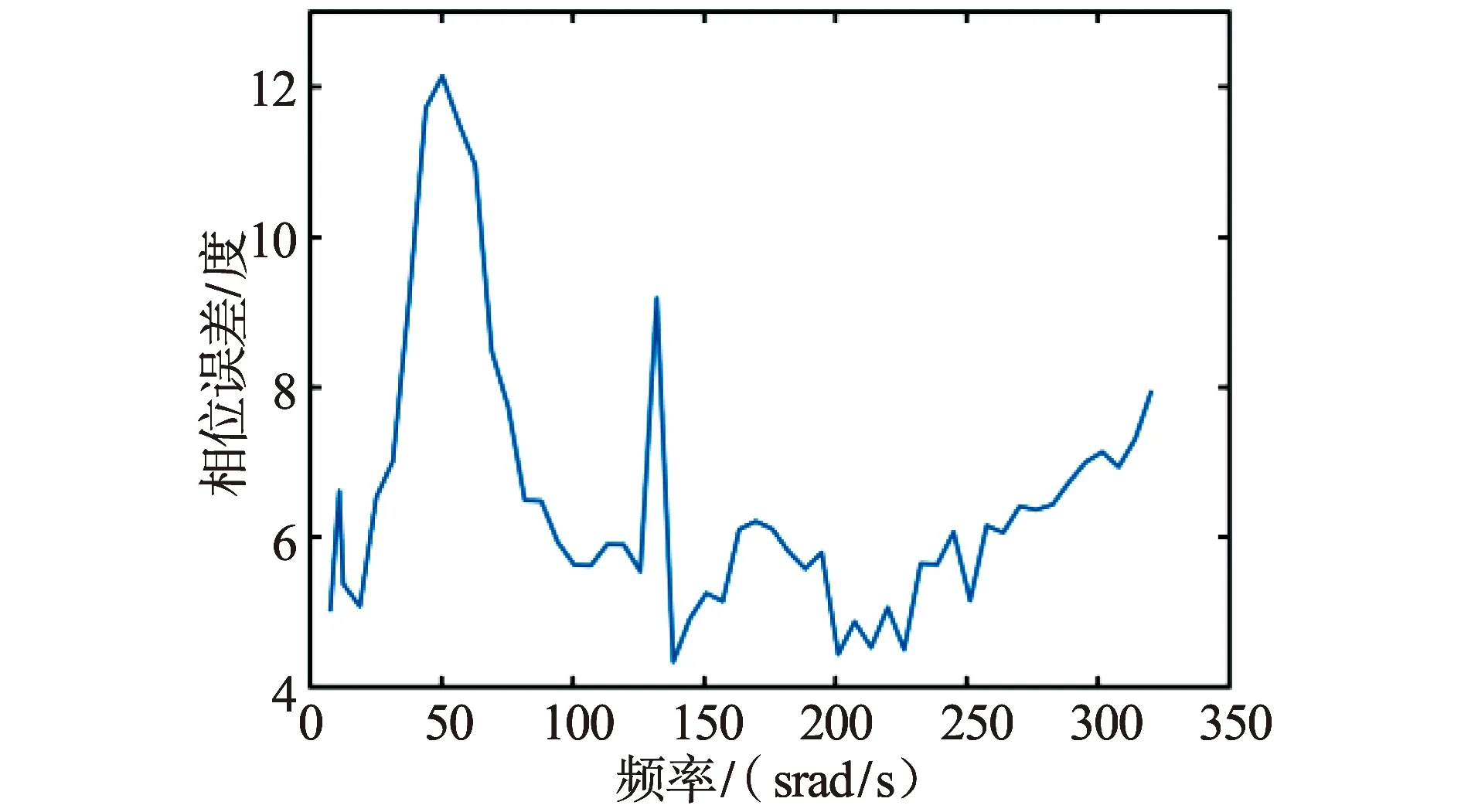
图8 传函相位误差图Fig.8 Transfer function phase error plot

(36)

实验结果表明,本文建立的传递函数模型能准确拟合音圈直线电机系统实际输出,精确的描述系统的频率响应特性。由实验结果计算得,相位误差和幅值最大误差率分别为5.583 8%和8.114 4%,误差在可接受范围内。

3.3 音圈直线电机滑模变结构控制实验

在如图4所示的实验台上进行了轨迹跟踪实验,实验结果如图9～图15所示。由公式(36)和2.1.2小节的分析,本文设计等效非线性项参数D=6 897 410.85。指令信号分别为:5 mm全行程连续步进信号,5 mm单步往返以及3 mm行程3阶S曲线,其中3阶S曲线中速度为6 mm/s,加速度为500 mm/s2,加加速度为100 000 mm/s3。

图9 全行程连续步进信号跟踪图Fig.9 Full-stroke continuous stepping signal tracking diagram

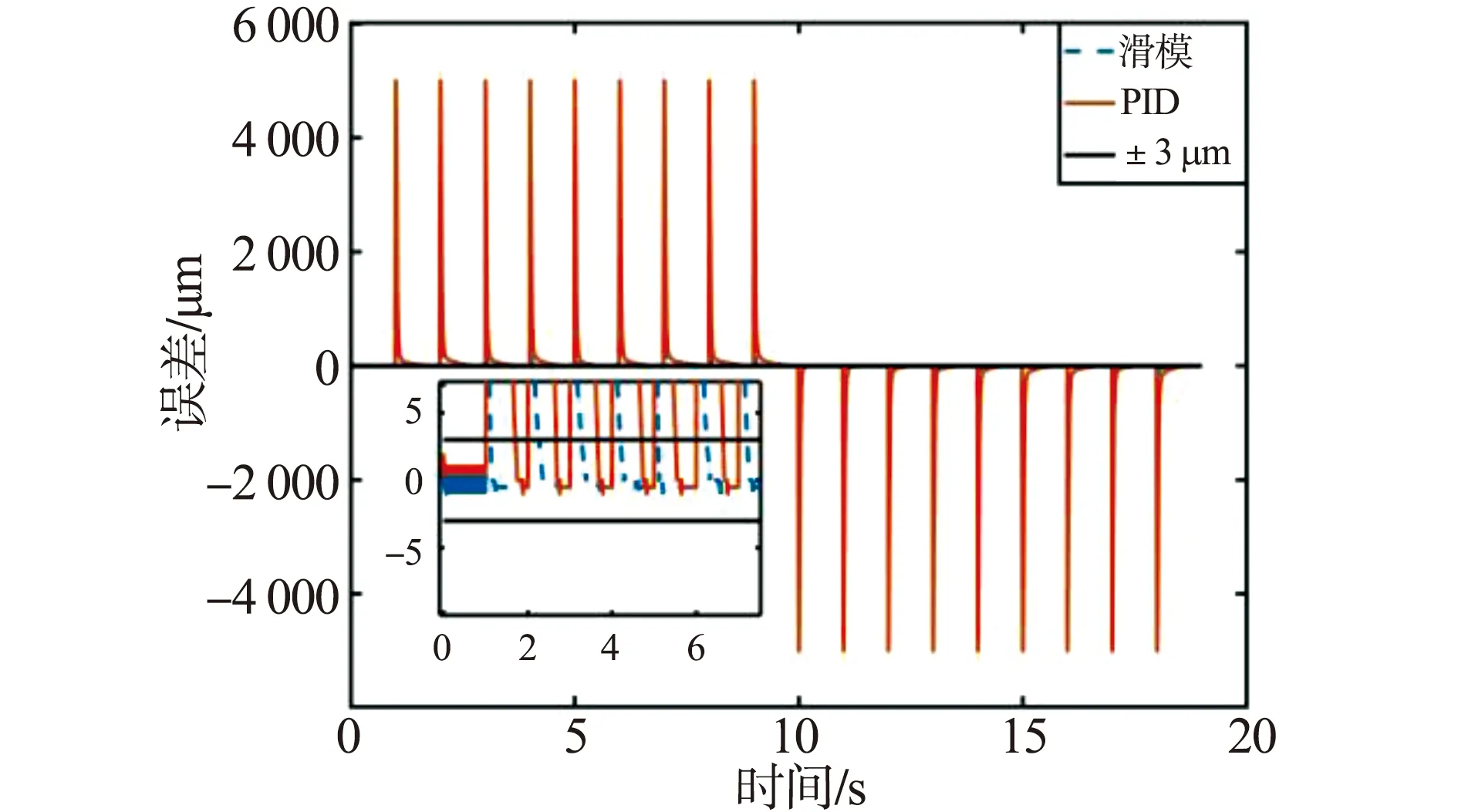
图10 全行程连续步进信号跟踪误差图Fig.10 Full-stroke continuous stepping signal tracking error plot

图11 5 mm单步往返信号跟踪图Fig.11 5 mm Single-step round trip signal tracking diagram

图12 5 mm单步往返信号跟踪误差图Fig.12 5 mm Single-step round-trip signal tracking error plot

图13 3阶S曲线跟踪图Fig.13 3rd-order S-curve tracking diagram

从实验图9至图15以及控制对比表2得出,在全行程5 mm连续步进阶跃指令下,滑模变结构控制方法的调节时间最长为600 ms,最短为70 ms,定位精度小于1 μm,稳态可达0.5 μm,PID控制方法调节时间最长为987 ms,最短为220 ms,定位精度小于1 μm,稳态可达0.5 μm。在全行程5 mm连续步进阶跃指令中,相较于传统的PID控制本文设计的滑模变结构控制方法的稳态性能和动态性能均有所提升;在5 mm单次往返指令中,所设计的滑模控制与PID控制使误差进入正负1 μm区间的调节时间分别为110 ms和854 ms,稳态误差均为0.5 μm;在3 mm的3阶S曲线指令中,所设计的滑模变结构控制与PID控制的最大误差分别为8 μm和58 μm,稳态误差分别为2 μm和10 μm。表2中的匀速段是指在3阶S曲线指令下,速度达到目标值且保持不变的一个时间段,很多的运动台都需要运动机构在匀速段达到相应指标,所以匀速段的相关指标是描述一个运动机构的重要指标之一。如图15所示,本文规划的3阶S曲线下对应的匀速段时间为0.108 7 s至0.501 7 s。表2列举了匀速段对应的位置最大误差、速度调节时间、速度最大误差的指标。由误差图14可知所设计的滑模变结构控制与PID控制在匀速段位置最大误差分别为6 μm和27 μm。由图15可知匀速段速度最大误差分别为0.729 3 mm/s和1.493 2 mm/s,所设计的滑模变结构控制在匀速段速度调节时间为127ms,PID控制在匀速段不能进入到速度终值的正负5%内。

表2 S曲线信号滑模变结构控制与PID控制对比表

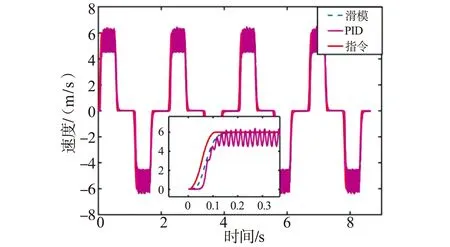
图15 3阶S曲线速度跟踪控制图Fig.15 3rd-order S-curve speed tracking control diagram

由上述分析可知,相比于传统的PID控制方法本文所设计的滑模控制器能够取得更好的控制效果,这是由于音圈直线电机系统中,存在不可忽略的非线性扰动,如非线性摩擦,所以提出控制方法的实验结果要明显优于传统的PID控制所得的实验结果。

4 结 论

为了消除非线性摩擦特性对音圈直线电机系统定位精度的影响,本文通过机理建模的方法建立系统的传递函数模型,采用最小二乘法辨识系统模型的参数。通过实验结果计算可得:模型幅值最大误差率为5.583 8%,模型相位最大误差率为8.114 4%。结果表明本文建立的模型可以准确地描述音圈直线电机的特性。为了达到精确定位精度的要求,基于已建立的音圈直线电机系统模型和摩擦力测试得到的非线性摩擦项,设计了线性等效控制项和非线性等效控制项,提出了一种滑模控制等效非线性控制项的参数设计方法。此外,根据采用李亚普洛夫稳定性理论证明了系统的稳定性。轨迹跟踪实验结果表明,提出的控制方法,有效的消除了非线性摩擦对音圈直线电机性能的影响。从实验数据还可以看出,相比于PID控制提出的控制方法具有更好的控制性能。本文提出的控制方法不但可以应用于音圈直线电机的轨迹跟踪控制,还可以应用到其他微纳米定位系统中。