基于数据驱动的风电机组变桨系统故障诊断与健康状态预测研究

尹子康,林忠伟,2,吕广华,李东泽

(1.华北电力大学控制与计算机工程学院,北京 102206;2.新能源电力系统全国重点实验室,北京 102206)

0 引 言

由于风的随机性,风电机组频繁的变桨动作导致变桨系统故障频发[1]。变桨系统作为风电机组实现风速调节和风机保护的重要装置,其故障主要表现为桨叶无法正常调节、桨叶无法停止转动、桨叶调节速度变慢或变快、桨叶转动角度偏差等[2]。这些故障会导致风电机组发电效率下降,甚至会对风电机组的安全运行造成严重影响。因此,变桨系统的保护和维护,以及及时检测和修复故障等问题受到了国内外众多学者的关注。

文献[3]提出了一种基于应变的自动操作模态分析算法,跟踪风电机组在运行条件下的长期动态行为,观察到由于叶片质量不平衡和塔振或塔后涡激励引起的基频和1f、3f激励频率的变化;文献[4]提出了一种基于气动力矩分析的叶片结冰和桨距角不平衡故障检测分析。该方法的主要优点是可靠性较高,但需要对系统进行深入的物理分析和建模,计算量大;文献[5]提出了一种基于自适应经验小波变换的提取行星齿轮相关振动成分,并通过包络谱识别故障特征的故障诊断方法;文献[6]提出了一种利用测量的信号纠正风力发电机转子桨距不平衡的新算法,不需要关闭发电机可以迭代地重新平衡转子。这种方法的优点是实时性好,但需要高效的传感器和通信技术;文献[7]提出了一种基于雷达风场重构和风条件聚类的数据驱动方法;文献[8]提出了一种应对现代风力发电机组桨距执行器故障的策略,通过合适的比例残差检测故障,并利用剩余的发电机扭矩和偏航执行器进行分布式控制。该方法的优点是实现相对简单,但当历史数据的质量和数量不高时会存在误差。

针对上述的故障诊断和故障预警的物理模型研究、统计模型分析、传感器和物联网技术的不足[9]。本文以风轮不存在质量不平衡为背景,利用GH-Bladed风机仿真软件仿真桨叶零位偏移故障,研究零位偏差对叶轮转速、叶根弯矩的影响,搭建桨叶零位偏差判定模型。机器学习和深度学习是当前故障诊断预警领域使用最多的方式[10]。本文基于神经网络技术,分析机组实际运行SCADA历史数据,完成变桨故障特征提取和数据分析处理,训练改进神经网络模型,构建AT-LSTM变桨健康状态预测模型。

1 风电机组变桨系统

变桨系统是风力发电机组中非常关键的一部分,其主要作用是通过调节叶片的桨距角来控制风对叶片的攻角,进而控制发电机输出功率,实现风电机组对风能的转换和最大化利用。

在风电机组正常运行过程中,变桨系统根据风速、输出功率以及发电机转速来改变叶片的桨距角,调整叶片与风能的接触面积,实现控制输出功率的目的[11],正常运行机组输出功率随风速变化曲线,如图1所示。

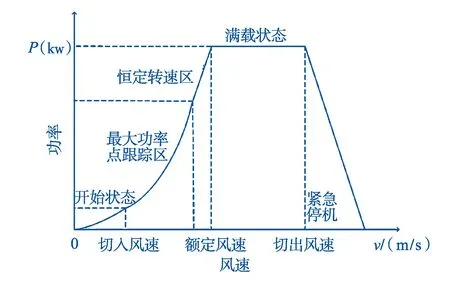
图1 风电机组输出功率-风速关系图Fig.1 Relation between output power and wind speed of wind turbine

当环境风速大于零且低于风力发电机组的切入风速时,风电机组进入开始状态,机组的状态将从停机转变为启动,风轮在风的作用下开始旋转。

当风速大于切入风速且小于额定风速时,风力发电机将开始进行并网发电,并将叶片角度设置为最小的桨距角。控制系统通过控制发电机转速来跟踪当前风速的变化,使风电机组处于最优风能状态[11-12];随着风速增大,发电机转速达到最大允许转速,由发电机系统控制发电机扭矩实现发电机转速进入恒定状态提升功率输出。

当风速处于额定风速和切出风速之间时,变桨系统和发电机系统配合主控制器分别控制桨距角及发电机转速,叶片的桨距角逐渐变大,降低桨叶中的扭矩,从而减少发电机组的输出功率,保证输出功率维持在额定功率值附近,发电机转速维持在同步转速附近,进而切入电网进行发电。

当风速高于切出风速时,机组需要紧急制动停机,期间完成顺桨指令将输出功率缩减为0并脱离电网,确保机组安全停运。

2 风电机组变桨系统桨叶零位校准

桨叶零位校准是一种用于修正风电机组变桨系统中机械侧故障的方法。当桨叶转动不均衡时,风电机组就会出现振动、噪音和效率降低等问题[13]。桨叶零位校准通过重新校准桨叶的角度来解决这些问题,使桨叶在风的作用下桨叶在平衡状态下运行,从而提高风电机组的效率和稳定性。桨叶零位偏差通常由桨叶安装不当、桨叶受损或桨叶零位校准不准确等原因引起的桨叶不平衡现象[14]。当桨叶处于不平衡运行状态时,其主要表现为转子不平衡,通过对转子不平衡现象的分析我们可以对桨叶零位偏差做出诊断。

本文采用GH-Bladed仿真软件对风电机组运行过程中桨叶零位偏移故障进行仿真,仿真采用GH-Bladed内置的2 MW陆上风电机组作为仿真机组模型,其机组参数如表1所示。

表1 仿真机组参数表Tab.1 Parameter table of simulation unit

由表1可以看出:仿真机组切入风速为4 m/s,切出风速为25 m/s,额定风速11.5 m/s。桨叶零位偏移故障是由于风电机组某一叶片初始位置偏移产生的。为应尽可能避开变桨控制过程,从而尽可能降低机组正常变桨控制过程中桨距角变化对实验结果的影响,仿真设置机组运行的平均风速区间从5-15.5 m/s变化,每段风速区间间隔为0.5 m/s,每段区间仿真时长600 s。仿真获取桨叶零位偏差角度从-5°～5°的转子转速、风速、叶根弯矩和机舱轴向加速度信号。桨叶零位偏差角的调整由于GH-Bladed软件故障仿真限制,采用每次增加1°的方式进行仿真。

2.1 桨叶零位偏差对机组参数的影响

对比桨叶零位发生正向偏移和反向偏移时,不同平均风速下风电机组转子转速的变化情况,如图2和图3所示。图中横坐标为仿真时间,纵坐标为风电机组转子转速,观察实验结果可以发现,当风速低于额定风速11.5 m/s时,随着机组桨叶零位偏差角的增大,机组在发生转速变化的时候其转速由于桨叶偏差的存在有明显的下降,造成转速下降的原因是由于桨叶零位偏差会使偏差叶片的桨距角增大,根据公式(1)可知,当桨叶出现零位偏移时,风机叶片的翼型攻角变小,导致风机转速下降。

图2 桨叶零位正向偏移时不同风速输入下的转速对比Fig.2 Comparison of rotor speed under different wind speed input when the blade zero position is shifted forward

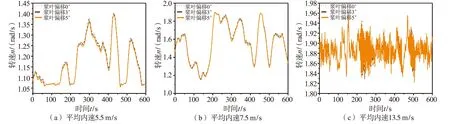
图3 桨叶零位反向偏移时不同风速输入下的转速对比Fig.3 Comparison of rotor speed under different wind speed input when blade zero reverse offset

θat=φ-θ0

(1)

公式中:θat为叶片翼型攻角;φ为入流角;θ0为桨叶零位偏差角度。

但当风机达到额定转速后机组变桨系统开始工作,风机的转速变化情况,如图2(c)和图3(c)所示。在平均风速为13.5 m/s时,由于变桨调节,零位偏差角度对风机转速的影响降低,风机的转速会在额定转速上下波动。

另一方面,对比了风电机组叶根弯矩Mx的变化情况,在平均风速为5.5 m/s和7.5 m/s时,风机叶片桨叶零位的正向偏移会导致偏差叶片的叶根弯矩波动幅度下降,如图4所示,可以观察到,当偏差角度越大时,其下降的幅度越明显;而当机组存在负偏差时,叶根弯矩受偏差的影响如图5所示,由于负偏差会使叶片真实的桨距角偏小,根据公式(1)分析可得,负偏差的存在会导致翼型攻角变大,从而导致叶根弯矩变化幅度随负偏差的角度增大而增大。

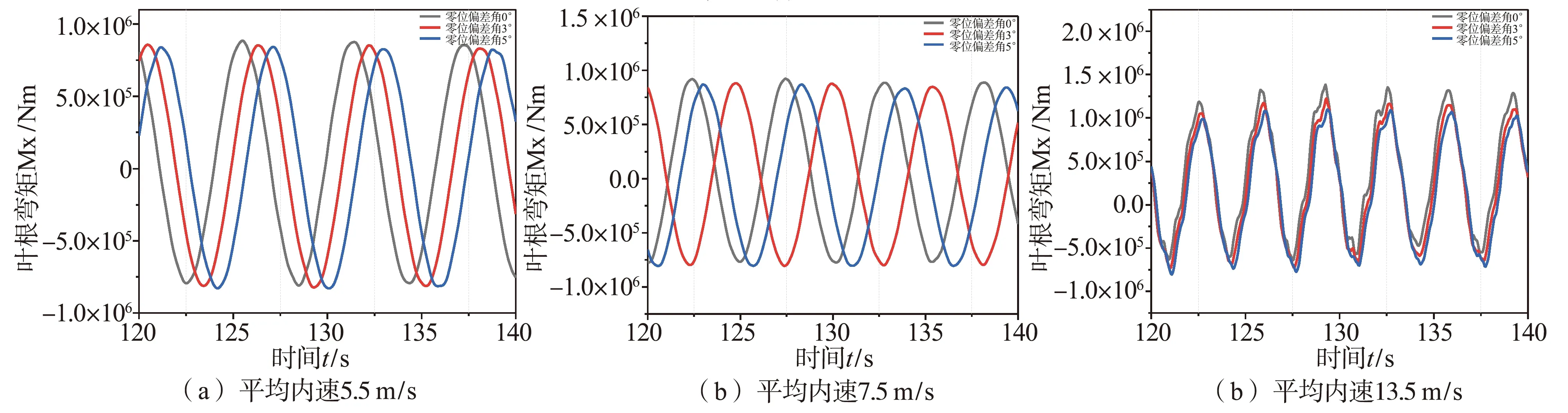
图4 桨叶零位正向偏移时不同风速下叶根弯矩对比Fig.4 Comparison of blade root bending moment under different wind speed when blade zero position is shifted forward

图5 桨叶零位反向偏移时不同风速下叶根弯矩对比Fig.5 Comparison of blade root bending moments at different wind speeds when blade zero reverse migration occurs

2.2 桨叶零位偏差故障识别诊断

桨叶零位偏移是一种机组叶片不平衡故障,在周期性响应的假设下,分析3叶片机组运行中的转子不平衡状态。当桨叶处于不平衡状态时,机舱轴向加速度信号经过FFT(傅里叶变换),可以检测到其他谐波分量,图6仿真记录了桨叶零位发生正向偏移时,平均风速为10 m/s下,机舱轴向加速度信号经过FFT(傅里叶变换)后的频谱。图6中分别标注出了1P(1/3风轮旋转频率)、1ST(一阶塔架固有频率)和3P(三倍风轮旋转频率)处幅值点,其中1P谐波最突出,因此转子不平衡的检测和校正可以基于1P谐波的测量分析展开。

图6 平均风速为10 m/s时不同偏移角度下机舱轴向加速度频谱图Fig.6 Spectrum diagram of axial acceleration of the engine room at different offset angles when the average wind speed is 10 m/s

分析当风电机组出现不同桨叶零位偏移角时,轴向加速度信号经过FFT,1P、1ST和3P处幅值随风速的变化情况。由图7所示,对比发现1ST和3P处幅值随风速的上升,整体波动较小,受桨叶零位偏移的影响也较小,而1P处幅值受桨叶零位偏移的影响比较明显,在高风速段,其幅值快速上升。此外还注意到,随着桨叶零位偏差角的增大,1P幅值开始快速爬升的平均风速节点不断前移,从图7(a)中可观察到,在桨叶零位未发生偏移时,平均风速大于13 m/s后1P幅值快速爬升,而图7(d)中,平均风速大于11 m/s后1P的幅值就出现了快速爬升的情况。另一方面,在相同风速下,当机组存在桨叶零位偏移时,其1P谐波的幅值随零位偏移角度的增大而增大,对比图7(b)、图7(c)和图7(d)发现这种现象在高平均风速的情况下更加明显。

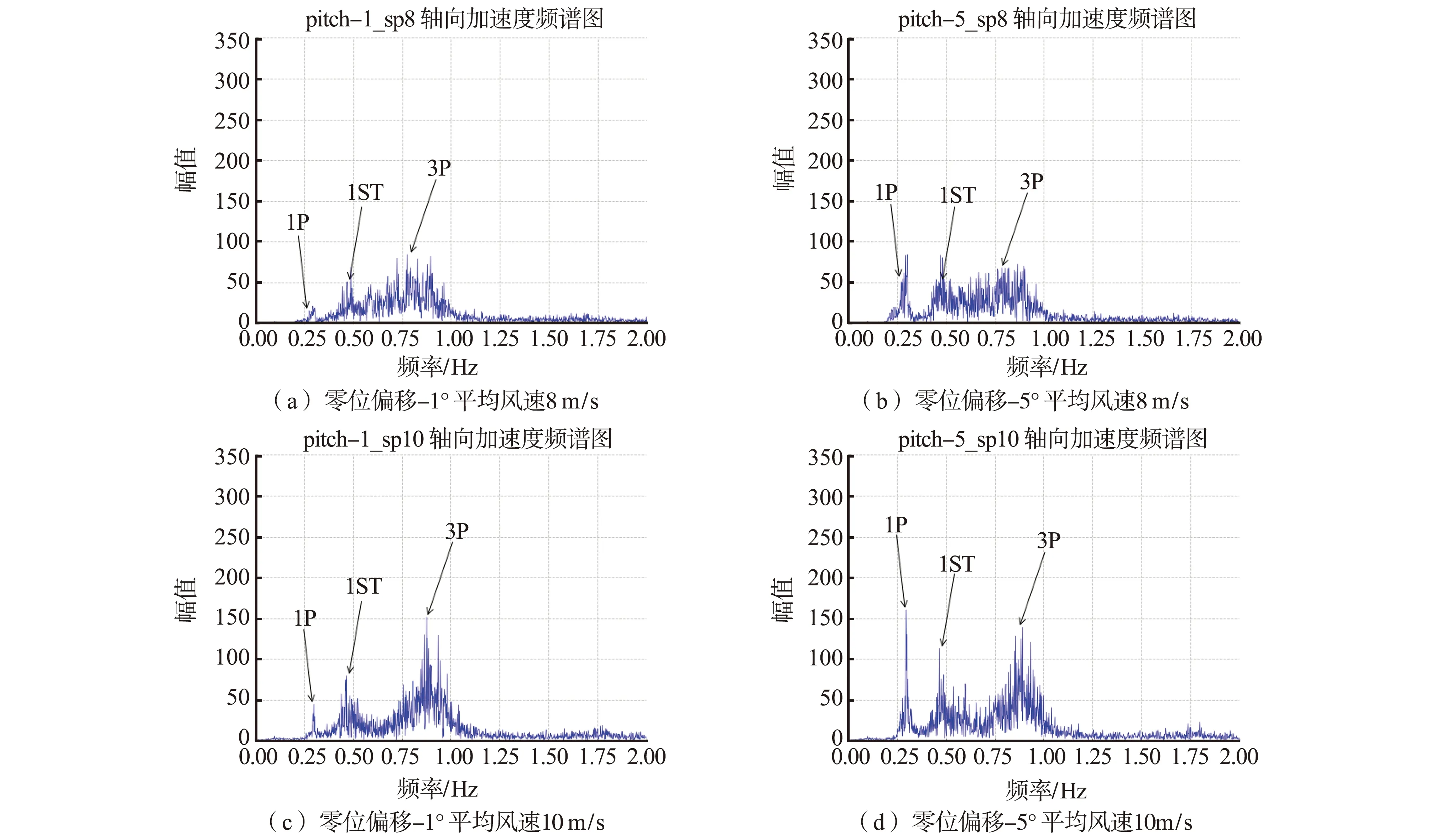
图7 不同桨叶零位偏移角度下轴向加速度频谱幅值变化Fig.7 Changes of spectral amplitude of axial acceleration under different blade zero offset angles

图8 桨叶零位偏差判定曲线图Fig.8 Curve diagram of blade zero deviation determination

判断风电机组桨叶零位偏移角度前,需要先判断机组发生的是正向偏移或是反向偏移,上文仿真对比了桨叶零位正向偏差时和反向偏差时偏差角对风电机组叶根弯矩的影响。考虑当机组存在正向偏差时,叶根弯矩随着偏差角度的增大而减小,而当机组存在反向偏差时,机组叶根弯矩随着偏差角度的变化趋势相反,随着偏差角度的绝对值增大,机组真实的桨距角变小导致叶根弯矩增大。基于这个结论,可对比诊断目标机组和标准机组不同风速下叶根弯矩的变化情况对机组发生桨叶零位偏移的方向做出判别,在确定机组偏移的方向后下一步需要进一步量化机组偏移的角度。

经过对不同工况下机舱轴向加速度信号傅里叶变换(FFT)后的频谱分析后提出了通过计算1P频率和3P频率处的幅值比θ,以平均风速为横坐标,幅值比θ为纵坐标,拟合桨叶零位偏差判定曲线,判定图如8所示。

实际工程应用时,可预先构建目标机组参数模型,通过多工况仿真拟合桨叶零位偏差判定曲线。然后通过传感器获取机组的机舱轴向加速度、风轮转速和风速等相关参数变量,计算机组运行的平均风速和平均风轮转速,再利用转速信号计算风轮旋转频率,获取1P幅值和3P幅值之比θ,以平均风速为横坐标,拟合出的θ作为纵坐标。在判定图上描出预警点。操作员可依据预警点所在的区间大致判断出桨叶零位偏差值。

3 风电机组变桨系统健康状态预测

在风电机组变桨系统故障诊断预警研究中,神经网络模型可以作为一种有效的故障诊断预警工具。通过使用大量的历史故障数据训练神经网络模型,得到一个比较高的诊断准确率。神经网络算法由于其强大的复杂非线性关系建模和处理大量数据的能力,近年来被广泛的应用于故障诊断和故障预警的相关研究中。不过,神经网络模型也有一些缺陷,如训练过程需要大量的数据和时间,模型的泛化能力可能不足等。

因此,在应用神经网络模型时,需要考虑到这些因素,本文考虑建立一种添加注意力机制的改进循环神经网络模型,通过准确率、召回率和F1-score等指标作为模型评价指标并与基础神经网络模型对比实验说明改进模型在故障诊断预警能力上的提升。

3.1 AT-LSTM模型

风电机组变桨系统发生故障时,不仅可以通过当前时刻的特征数据反映,而且还能通过当前时刻之前的一段时间的特征数据变化反映。针对这一现象,本文使用LSTM来反映一段时间内特征数据与风电机组变桨系统故障之间的内在联系。但是,由于LSTM对所有信息进行无差别压缩,从而忽略特征之间的相关性和输入信息的时间差异[15]。因此,本文在LSTM基础上,引入注意力机制。注意力机制是一种资源分配机制,可自适应地为输入信息分配注意力权重,以评估不同输入对期望输出的贡献率,并突出重要输入信息的影响[16-17]。在机器翻译[18]、语音识别[19]等领域,注意力机制已在许多不同的应用中被证明是有效的。

3.1.1 LSTM模型

长短期记忆(Long Short-Term Memory,LSTM)是一种递归神经网络(Recurrent Neural Network,RNN),主要用于处理序列数据,如时间序列数据或自然语言文本。相较于传统的RNN,LSTM可以更好地捕捉长期依赖关系,避免了梯度消失的问题。

LSTM网络结构如图9所示,整个网络内部结构由门结构组成,具体由sigmoid函数、tanh函数和逐点相乘相加的结构实现。在遗忘门中,以前一时刻输出ht-1和当前时刻输入数据xt作为输入,通过一个激活函数sigmoid和偏置,输出结果为ft。结果为0～1之间,0代表信息全部丢弃,1代表信息全部保存,0～1之间代表前一时刻状态信息通过的比重。

图9 LSTM神经网络结构图Fig.9 LSTM neural network structure diagram

ft=σ(Wf·[ht-1,xt]+bf)

(2)

公式中:σ为sigmoid函数;bf为遗忘门偏置。

在输入门中,LSTM网络将前一时刻输出ht-1和当前时刻数据输入xt,通过计算得到it及通过暂时状态ĉt。通过利用遗忘门结果和输入门暂时状态信息更新网络单元状态信息ct。

it=σ(Wi·[ht-1,xt]+bi)

(3)

(4)

(5)

公式中:σ为sigmoid函数;Wi、Wc分别为输入门权重;bi、bc为输入门偏置。

在输出门中,LSTM网络以前一时刻输出ht-1和当前时刻输入数据xt作为输入,通过一个激活函数sigmoid和偏置得到ot,并结合当前单元状态ct,利用tanh函数得到最终输出ht。

ot=σ(Wo·[ht-1,xt]+bo)

(6)

ht=ot·tanh(ct)

(7)

公式中:σ为sigmoid函数;Wo为输出门权重;bo为输出门偏置。

以上公式中权重和偏置会一般采用循环神经网络的训练算法,通过计算单元输出值和误差项,不断更新权重和偏置。通过以上方式,LSTM模型以链路结构形式,基于门结构控制形式将时序数据顺序传递,完成对海量信息的挖掘。

3.1.2 注意力机制

注意力机制旨在帮助网络专注于给定输入中最重要的信息。其背后的基本思想是根据需要多少注意力为输入数据的不同部分分配权重。然后网络使用这些权重来确定哪些信息需要更多关注,哪些信息应该忽略,使网络能够动态地关注输入中最重要的信息,从而提高其整体性能。

神经网络编码-解码是指使用神经网络实现数据的编码和解码的方法。具体地说,编码器会对原始数据进行压缩,以便以更高效的方式存储和传输数据,而解码器则会还原被编码的数据。使用神经网络编码-解码,可以用于降维、数据去噪、模型压缩等任务。神经网络比较典型的编码-解码框架是Encoder-Decoder(编码-解码)模型框架,其详细结构如图10所示。

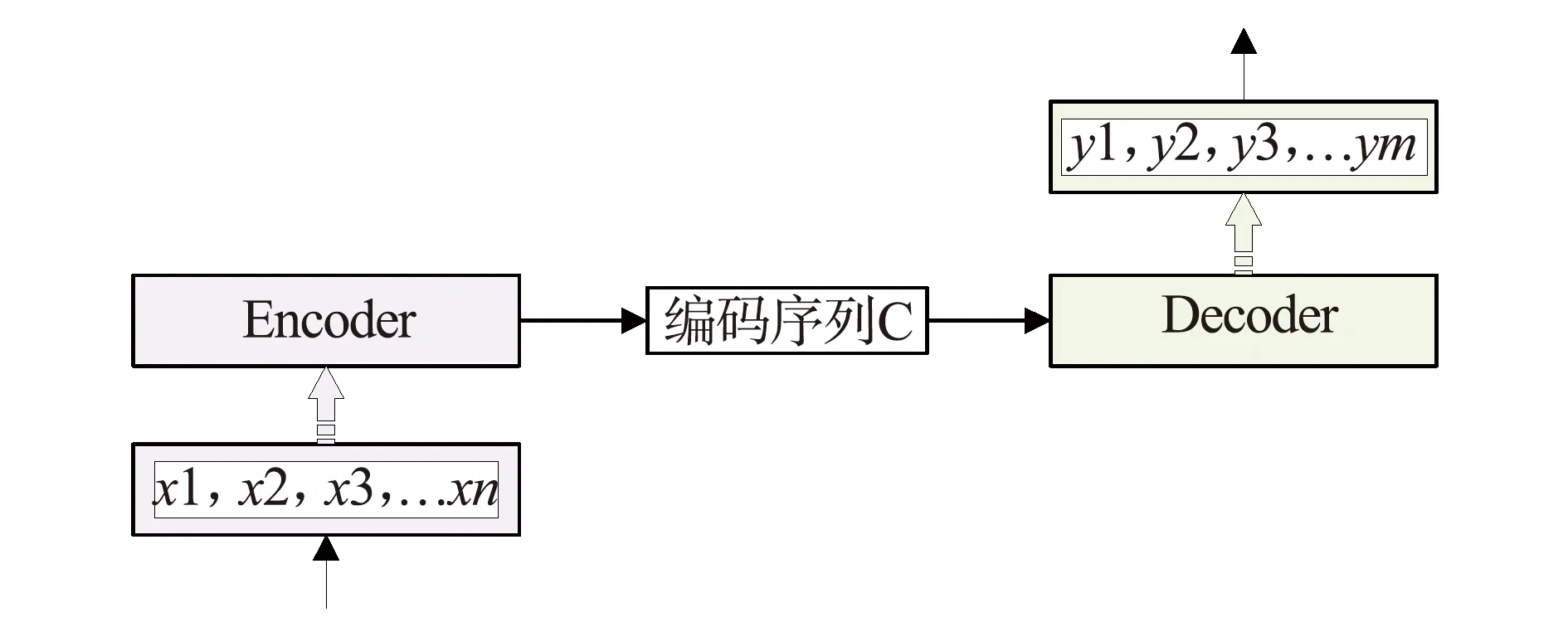
图10 Encoder-Decoder(编码-解码)模型框架Fig.10 Encoder-Decoder model framework

本质上其是一种End-to-End的学习框架,输入信号经过编码层(可以由RNN、LSTM、GRU和CNN等不同的网络层组成)将输入序列编码加工成一个固定长度的向量,解码则是将之前生成的向量转化成输出序列的过程[20]。可以用数学过程简单的描述神经网络编码-解码的过程。

X=(x1,x2,x3,…,xm)

(8)

Y=(y1,y2,y3,…,ym)

(9)

C=f(x1,x2,x3,…,xm)

(10)

yi=g(C,y1,y2,…,yi-1)

(11)

其中,公式(10)为Encoder过程,公式(11)为Decoder过程。从数学表示式子中不难发现,固定向量C作为信号传递的中间项,其传递过程中微小的权重变换都会导致传递的信息不同。

根据注意力机制的工作原理可以构建如公式(12)的数学模型。

(12)

公式中:αi为相关度;q为特征条件;xi为输入向量第i条信息。

图11总结了注意力机制工作的过程,在第一步,特征查询条件和输入信号进入神经网络编码层S,编码层将信号xt映射到ht,公式(13)反应了这个映射的过程。

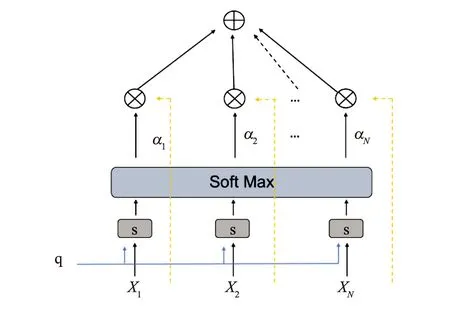
图11 注意力机制工作原理图Fig.11 Working principle of attention mechanism

ht=f1(ht-1,xt)

(13)

公式中:f1为非线性激活函数;ht为t时刻的隐藏状态,本文构建的故障预警模型为添加注意力机制的改进LSTM模型,所以模型编码层和解码层均为LSTM网络层,下面解释均以LSTM网络层来说明。对于某一个特征序列x=(x1,x2,x3,…,xN)T,该序列通过LSTM网络层后,其隐藏状态和单元状态可用公式(14)表示。

βt=vTtanh(W1·[ht-1,Ct-1]+W2x)

(14)

(15)

at=(α1x1,α2x2,α3x3,...αNxN)T

(16)

其中,向量v、向量W1和W2为学习参数,向量βt表征了第t个输入的重要性,如公式(15)每个参数的重要性被softmax函数归一化为权重αt,它表征了第t个特征序列应该投入多少注意力的得分,然后利用公式(16)计算新的特征序列作为LSTM神经网络模型的输入,理论上,新的特征输入序列对故障特征的表示能力更强。

3.2 数据预处理

本文以某风场2020年7月1到2020年8月24日E10机组运行SCADA数据,数据采样频率为1分钟,已明确机组于2020年7月发生变桨故障并于7月9日停机检修,故将检修前机组运行数据作为故障数据,检修后数据作为正常运行数据。其中故障数据11 138条,正常运行数据11 461条。

3.2.1 特征量选取

SCADA数据涉及多个变量,如风速、功率发电机转速,线电压等,但是,并不是所有的变量都对模型有用,某些无关的特征可能导致欠拟合,使得故障检测性能下降[21]。所以,使用皮尔逊相关系数计算每个变量之间的相关性,如公式(17)所示。

(17)

由于本文关注变桨系统的故障问题,而变桨控制主要控制叶片的角度来实现,因此在特征提取时,关注各变量和叶片角度变化的相关性情况,变量相关性热力图如图12所示。

图12 特征量相关性热力图Fig.12 Correlation heat maps of characteristic quantities

通过热力图颜色深浅程度和相关性系数的绝对值分析比较完成对原始数据的相关性分析,提取了机组和叶片角度相关性最强的13个特征数据作为故障诊断预警模型的输入特征,其特征参数表如表2所示。

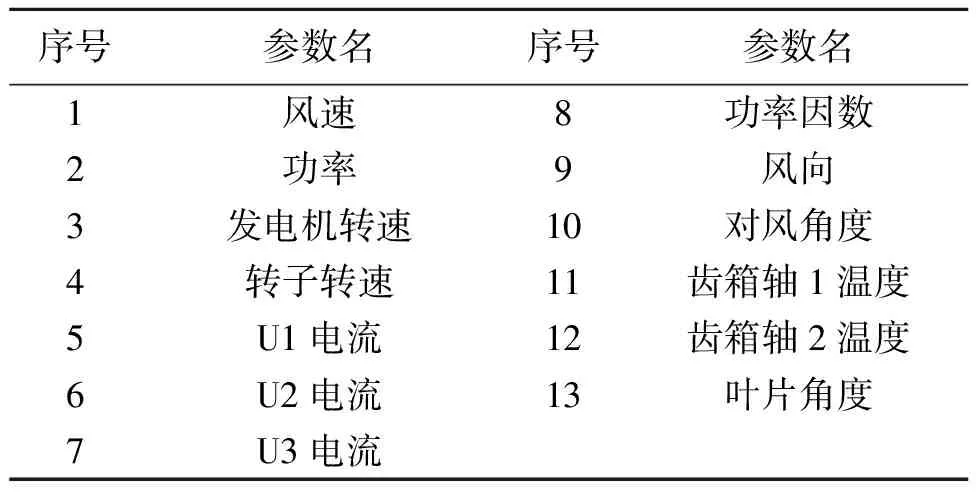
表2 特征参数表Tab.2 Feature parameter table

3.2.2 数据归一化

数据归一化是指将不同取值范围的特征转换为同一尺度的过程。上文通过特征提取获取了13个特征的风电机组SCADA数据,每个特征代表一列时序数据,而不同特征变量采用的单位和量纲不同,直接作为神经网络模型输入会造成模型中神经元饱和,产生梯度消失或者梯度爆炸的问题,从而使模型的收敛速度变慢,训练难度加大。因此在输入神经网络模型之前需要进行归一化处理。本文采用最小-最大归一化的方式将特征值缩放到[0,1]的范围内,如公式(18)所示。

(18)

公式中:xmin为样本最小值;xmax为样本最大值。

3.2.2 数据切片

数据切片是指将数据集按照一定的规则分成多个子集的过程。数据切片通常用于数据挖掘和深度学习中的交叉验证和训练测试集划分。通过多次交叉验证,可以评估模型的性能并选择最优的模型参数。在进行模型训练的数据集划分时,将数据集划分为训练集和测试集两部分,其中训练集用于模型的训练和参数调优,测试集用于评估模型的性能。常用的数据切片方法包括随机切片、分层切片等。

本文实验数据为时序数据,因此采用滑动窗口的方式做分层切片,由于期望诊断预警模型具有一定的预警能力且尽可能保留数据多样性,因此考虑以60为滑动窗口的大小,滑动步长为1。滑动窗口模型如图13所示。

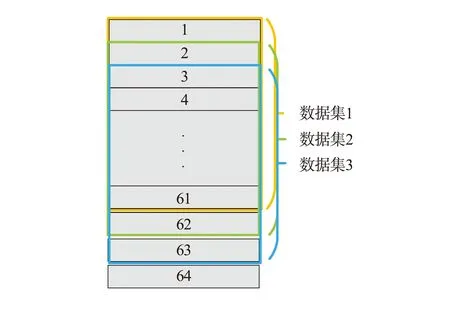
图13 滑动窗口示意图Fig.13 Schematic diagram of sliding window

滑动窗口的大小为60,表明故障预警模型每次的输入数据为当前时刻下前60分钟的全特征数据;滑动步长为1,表明模型每分钟更新一次输入数据集。

3.3 构建健康状态预测模型

通过网络学习设备状态的时序特征,从而实现对设备状态的故障诊断预警。模型采用滑动窗口和多层AT-LSTM网络等技术,以进一步提高模型的准确性和稳定性。基于AT-LSTM神经网络模型结构如表3所示。

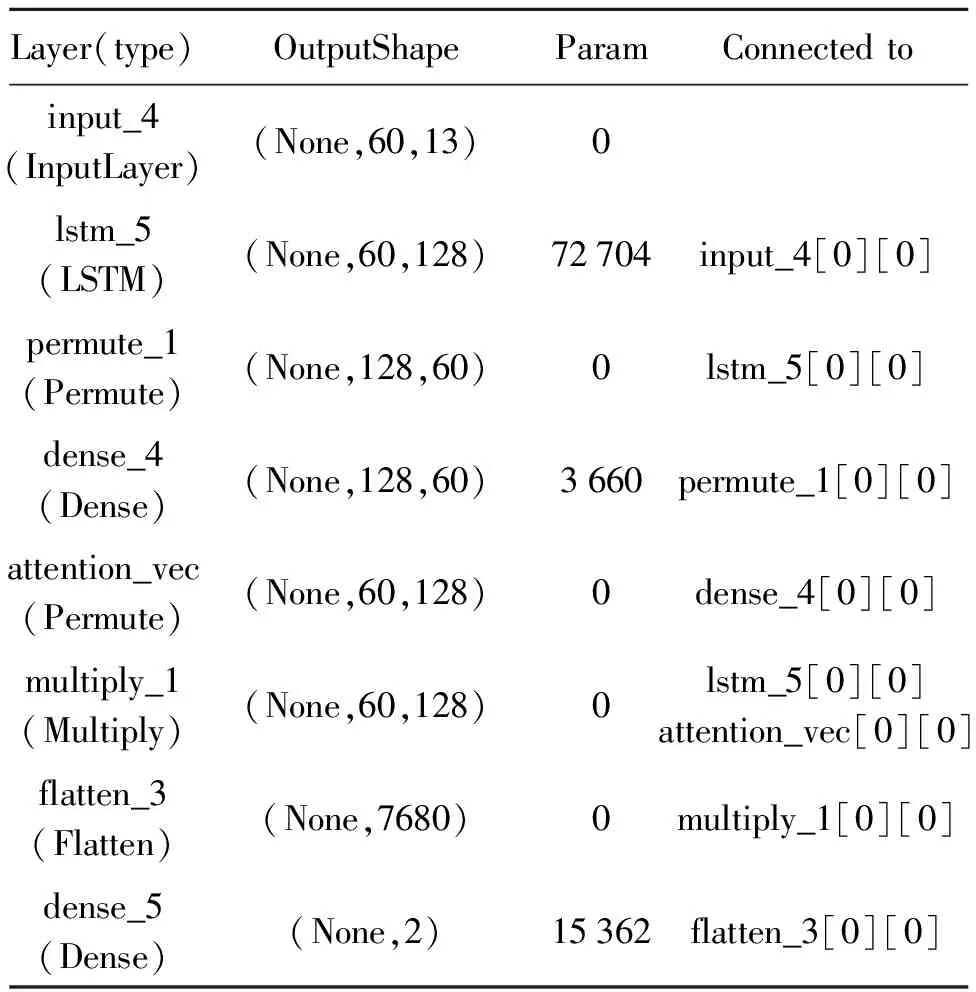
表3 AT-LSTM神经网络模型结构表Tab.3 AT-LSTM neural network model structure table

基于滑动窗口的切片方式,将完成归一化之后的特征数据构造成为shape为(None,60,13)的三维数据,其中第一个维度表示进入模型的训练集的数量,在输入层可以不用定义,第二个维度和第三个维度表示模型训练数据集的特征为60×13的张量。利用LSTM神经网络层构建Encoder(编码层)和Decoder(解码层),在编码层后通过Permute层添加注意力机制,然后将三维shape展成二维的Flatten层,最后通过Dense全连接层输出。

由于建模的目标实质上是解决一个二分类问题,因此选择Adam作为网络模型的优化求解器,模型的学习率为0.000 01,选择较小的学习率是为了使神经网络模型训练趋向稳定,尽可能避免无法收敛导致模型学习能力下降的情况。另一方面,由于故障诊断预警模型的输出是对于故障发生概率的预测结果,因此在选择激活函数时,以softmax作为激活函数对于本模型来说是比较合适的选择。在完成基本的建模操作以后,取故障数据集和正常运行数据集的前80%作为模型训练集数据,后20%作为测试集数据,输入当前时刻下的特征数据集,预测下一个输入周期机组处于故障运行状态或是正常运行状态实现故障预警。

3.4 健康状态预测模型评价

对比了改进后的AT-LSTM神经网络模型、循环神经网络(RNN)模型和基础LSTM神经网络模型,从多个分类模型指标出发,分析增加注意力机制对神经网络模型带来的提升。构建基本RNN神经网络模型和LSTM神经网络作为实验对照组,在相同训练集和测试集的输入下,其中,故障运行样本个数为2 208、正常运行样本个数为2 281。对比不同健康状态预测模型的f1-score等指标情况,如表4示,其中,macro avg(宏平均)为所有类的F1算术平均,weighted avg为每个类别样本数量占总样本的比例。除了对模型预测指标的分析,通过对预测模型的ROC曲线对比,也能更直观的体现出添加注意力机制之后改进模型预测性能更加优秀,三个模型的ROC曲线如图14所示。

表4 不同模型故障诊断评价参数对比

图14 不同模型ROC曲线对比图Fig.14 Comparison of model ROC curves

改进后的AT-LSTM神经网络模型具有更加优异的分类准确率和较低的预测样本遗漏比率,分类器真正例率较高,在各种阈值下具有较好的表现,分类预测的性能也优于对照模型。训练好的故障诊断预警模型可实现基于风电机组变桨系统健康状态的有效监测和提前预警,由于训练时采用的数据集长度为60,训练所用的数据集为风电机组1 min的运行数据,因此故障诊断预警模型能有效预测机组1 h后的变桨系统健康状态,实现机组故障的提前预警。

4 结 论

聚焦风电机组桨叶零位偏移故障,从理论上论证分析了桨叶零位偏移产生的风电机组转子不平衡现象和机舱轴向加速度信号1P谐波幅值之间的联系,继而使用GH-Bladed风机仿真软件对桨叶零位偏移角度从-5°到5°变化情况进行仿真,通过设置不同的平均风速条件,对比分析不同工况下桨叶零位偏差对转速、叶根弯矩和1P幅值的影响,提出计算1P幅值和3P幅值之比并将其拟合为桨叶零位偏差判定曲线图。利用风电机组SCADA历史数据,考虑基于AT-LSTM改进神经网络构建变桨系统故障诊断预警模型,模型的主要目标在于依据已查明故障节点的SCADA历史数据训练出适用于对应风电机组的故障诊断预警模型。从多项分类指标出发将AT-LSTM模型、RNN模型和LSTM模型进行对比,添加注意力机制后的AT-LSTM神经网络模型具有更好的分类预测能力。AT-LSTM模型由于添加注意力机制,可以自动地关注输入序列中最重要的部分,加强了模型对于长期依赖关系的建模能力,具有较好的鲁棒性且适用性广泛。