基于MATLAB/Simulink仿真的永磁同步电机新型超螺旋二阶滑模转速控制
胡启国, 王泽霖*, 胡豁然
(1. 重庆交通大学机电与车辆工程学院, 重庆 400074; 2. 国网重庆市电力公司信息通信分公司, 重庆 401120)
永磁同步电机(permanent magnet synchronous motor,PMSM) 较其他电机具有体积小、效率高、功率密度大等优点[1],且随着高级永磁材料的快速发展,其已被普遍应用于新能源汽车、工业制造等领域。在PMSM矢量控制系统中,转速外环控制是较为关键的控制环节,传统的转速外环控制一般采用比例积分(proportional integral,PI)控制,但该方法不仅动态响应能力弱,且对系统内外扰动的自适应性较差。为此,取代PI转速控制,设计一种拥有强鲁棒性与收敛性的转速控制方法变得至关重要。
滑模控制技术凭借其结构简单、响应快、鲁棒性强[2]等特点,已逐步取代PI控制技术,并在PMSM转速控制领域广泛应用,但滑模控制容易使系统产生抖振,也成为其一大缺点。为了削弱滑模抖振,改善滑模运动的动态品质,通常采用趋近律方法[3]设计滑模转速控制器。然而,趋近律参数的设定较为严谨,一旦参数值选择不当,依然会引起较大的信号抖动,因而该方法不能够从根本上解决抖振问题。近些年来,高阶滑模控制技术不断吸引着众多学者的目光,此技术与趋近律滑模等一阶滑模控制相比,进一步加强了系统鲁棒性且能够很好地抑制抖振,从而在滑模控制中逐渐占据主导地位。超螺旋算法[4]由于不需引入新控制变量,输出连续且可大幅度减小抖振,因此在高阶滑模中被普遍采用。王朕等[5]向超螺旋算法中引入自适应律,设计了自适应超螺旋转速滑模控制器,更好地抑制了PMSM转速超调。金爱娟等[6]基于原有超螺旋算法,引入自适应比例项和积分项,搭建了改进的超螺旋滑模转速控制器,更进一步提高了PMSM系统的收敛速度。程涛等[7]采用饱和函数代替原超螺旋算法中的开关函数,设计了改进的超螺旋滑模转速控制器,进一步抑制了PMSM转矩抖振。
文献[5-7]在原有超螺旋算法基础上做了相关改进,并用于PMSM转速控制,取得了较好地控制效果,但针对超螺旋算法的改进均偏于局限,未能全面的考虑超螺旋算法的不足。鉴于此,为更好地改善超螺旋算法,从收敛速率、控制精度及抖振等多方面考虑,对传统超螺旋算法做出进一步改进,提出一种新型超螺旋算法,包括设计了变指数取代原算法中非线性项的常指数以改善算法收敛性能,引入分数阶微积分取代整数阶以提高算法计算精度,设计变边界层非线性指数函数代替开关函数以削弱系统抖振。最后,结合新型超螺旋算法,设计PMSM新型超螺旋二阶滑模转速控制器,并进行仿真对比分析,过程中采用鲸鱼算法优化控制参数,结果证实了所提方案的可行性。通过此项设计研究可为PMSM控制系统的动稳态性能改善提供一份参考。
1 PMSM数学模型
相较于内置式PMSM,表贴式PMSM制造成本低、电流响应快且转动惯量小。因此,以表贴式PMSM为研究对象,忽略定子铁芯饱和及其他各种损耗等,建立电机定子电压方程、电磁转矩方程与运动方程[8]分别如式(1)、式(2)与式(3)所示。
(1)
式(1)中:ud、uq与id、iq分别为d-q轴坐标系,即两相旋转坐标系下的定子电压与电流;Rs为定子相电阻;Ld、Lq分别为d-q轴坐标系下的电感,且Ld=Lq=Ls,其中Ls为定子等效电感;ωr为转子角速度;ψf为永磁体磁链;t为时间。
Te=pnψfiq
(2)
式(2)中:Te为电磁转矩;pn为电机的极对数。
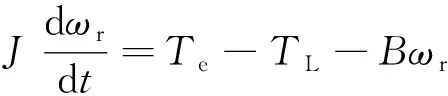
(3)
式(3)中:J为转动惯量;TL为负载转矩;B为黏滞摩擦系数。
2 新型超螺旋二阶滑模转速控制器设计
2.1 超螺旋算法理论
超螺旋算法的最大特点即为系统状态是在有限时间内以螺旋式地运动轨迹围绕着原点向其收敛。该算法的基本结构[9]可表示为
(4)
式(4)中:s为滑模变量;y为中间变量;sgn为开关函数;KP、KI为滑模增益,且KP> 0,KI> 0;ρ1、ρ2为干扰项。
2.2 超螺旋算法改进


(5)
由式(5)可知,函数g(s)的值域为(0,1),指数值将在此范围内进行调整。将式(5)代入式(4),可得改进后的非线性项变为|s|g(s)。当|s| > 1时,系统状态离滑模面较远,此时|s|g(s)值较大,可有效地加快系统状态的趋近速率,较大地缩短趋近时间;当|s| ≤ 1时,系统状态离滑模面较近,此时|s|g(s)值较小,能够保证系统状态较为平滑地切入滑模面,增强其稳定性。
为能更好地提高超螺旋算法的控制精度,采用分数阶控制法代替传统超螺旋算法中的整数阶控制。分数阶理论自诞生起在各工程领域均得到了实际应用,并已通过实验证明了该理论的有效性和实用性,它可准确地描述问题的基本现象[10],解得的结果与实际情况更相符,从而赢得了越来越多的关注。常见的分数阶主要有Riemann-Liouville式、Grunwald-Letnikov式与Caputo式,其中,针对本文情况,选用Caputo式分数阶[11],其通用表达式为
(6)
为更进一步地减小系统抖振,增强系统运行时的平稳性,设计一种边界层可变的非线性指数函数,以取代传统超螺旋算法中的开关函数。所设计函数可表示为
(7)
式(7)中:γ为常数, 0<γ< 1;δ为常数,δ> 0;|δtanh(s)|为边界层。
综上所述,将式(5)、式(6)与式(7)代入式(4)中,可得新型超螺旋算法为
(8)
式(8)整理后也可变成式(9)所示形式。
(9)
式(9)中:ρ为干扰项。
2.3 有限时间收敛验证
现对新型超螺旋算法的有限时间收敛性进行证明。对于式(8),忽略扰动量,取向量

(10)
对式(10)求α阶导,得
(11)
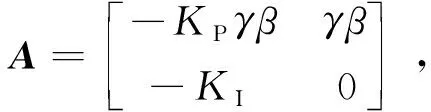
Δ2+γβKPΔ+γβKI=0
(12)
因KP、KI> 0且通过证明可得γβ> 0,则对于任意的正定矩阵Q,必定存在一正定矩阵P,满足于方程ATP+PA= -Q,据此可取Lyapunov函数为
V=ζTPζ
(13)
对式(13)求α阶导,得

(14)
由于函数V为二次型正定函数,则有

(15)

由式(15)可得
(16)
同样可得
(17)
结合式(14)可推得
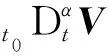
≤-λmin(Q)‖ζ‖2
(18)
综合式(17)与式(18),最终可得

(19)
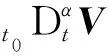
2.4 超螺旋算法验证
为更进一步验证所提新型超螺旋算法的可行性,现引入典型的带有建模不确定和外部干扰信号的二阶非线性系统为被控对象,该系统表示为
(20)
式(20)中:x1和x2为系统状态变量;x= [x1,x2]T;f(x,t)为连续函数;Δf(x)为系统的建模不确定项;d(t)为外部的干扰信号;u(t)为控制输入,通过控制器u(t),对二阶非线性系统进行平衡控制,状态变量渐进收敛到零。
分别用传统超螺旋算法和新型超螺旋算法设计控制器u(t)。
令s为
s=x2+cx1
(21)
结合式(4)、式(21),得采用传统超螺旋算法设计的控制器u1(t)可表示为

cx2-f(x,t)-Δf(x)-d(t)
煤矿机电自动化技术的广泛应用是提高煤矿开发利用效率的重要保障,也是减少机械故障,提高煤矿生产安全性和可靠性的重要措施。煤矿机电自动化技术在煤炭传送系统、矿井提升机、牵引采煤机和矿井监测系统中得到了一定的应用。随着机电自动化技术的不断发展,煤矿机电自动化在煤矿生产中占据的地位也越来越重要,对促进煤矿机电设备向智能化发展有着积极的促进作用。
(22)
同理,结合式(9)、式(21),得采用新型超螺旋算法设计的控制器u2(t)为

cx2-f(x,t)-Δf(x)-d(t)
(23)
对式(22)、式(23),令
(24)
利用MATLAB分别搭建式(22)、式(23)所示控制器模型,仿真后得u1与u2的响应曲线如图1所示。

图1 控制器响应曲线Fig.1 Curves of controller response
由图1可以看出,相较于u1曲线,u2曲线进一步降低了初始超调,更加平缓了收敛后的曲线波动。由此表明,新型超螺旋算法在收敛性及稳定性等方面均优于传统超螺旋算法。
2.5 滑模转速控制器设计
采用新型超螺旋算法,设计PMSM新型超螺旋二阶滑模转速控制器。具体如下。
(25)

结合式(3)、式(9)与式(25),可得
(26)

(27)
3 仿真分析
利用MATLAB/Simulink对设计的PMSM新型超螺旋二阶滑模转速控制器进行仿真分析,同时与采用传统超螺旋算法及指数趋近律设计的滑模转速控制器相比较。其中,采用传统超螺旋算法设计的超螺旋二阶滑模转速控制器的控制律[12]可表示为
(28)
式(28)中:s=eωr。
采用指数趋近律设计的指数趋近律滑模转速控制器的控制律[13]可表示为
(29)
结合id= 0定子电流控制策略与逆变器空间矢量脉宽调制(space vector pulse width modulation,SVPWM)技术,利用MATLAB/Simulink搭建PMSM滑模转速矢量控制系统模型,其控制框图如图2所示,该控制系统为转速电流双闭环控制系统。其中,电流环控制器采用PI控制器,转速环控制器采用滑模控制器,且滑模控制器的控制律分别采用式(27)~式(29)所示形式。

为id、iq的给定值;uα、uβ与iα、iβ分别为α-β轴坐标系,即两相静止坐标系下的定子电压与电流;θr为转子位置角;udc为直流电压;iABC为定子三相电流图2 PMSM滑模转速矢量控制系统框图Fig.2 Diagram of PMSM sliding mode speed vector control system
仿真前,设定PMSM参数如表1所示。电流环PI参数设为:kP= 60,kI= 6 000。采用寻优能力强的鲸鱼优化算法[14](whale optimization algorithm,WOA)对指数趋近律滑模转速控制器参数,即式(29)中c、ε、k,传统超螺旋二阶滑模转速控制器参数,即式(28)中KP、KI以及新型超螺旋二阶滑模转速控制器参数,即式(27)中KP、KI、k1、k2、k3进行寻优整定。
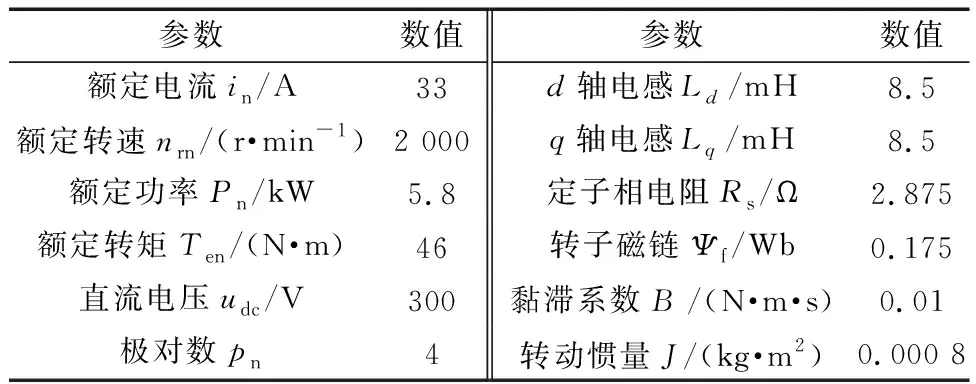
表1 PMSM参数Table 1 PMSM parameters
采用分段混沌映射法[15]初始WOA种群,并设定种群数量S= 100,最大迭代次数M= 100,适应度函数选用时间乘以误差绝对值积分(integrated time and absolute error,ITAE)指标,可表示为

(30)
以上述待优化参数为设计变量,以ITAE指标为适应度函数,在MATLAB中利用WOA对ITAE进行20次仿真求解,并将20次仿真中每次迭代求得的最优参数值的平均值随迭代次数的变化曲线绘制于图3,同时将其最终迭代得到的最优参数值的平均值如表2~表4所示。

表2 指数趋近律滑模转速控制器Table 2 Exponential reaching law sliding mode speed controller

表3 传统超螺旋二阶滑模转速控制器Table 3 Traditional super twisting second order sliding mode speed controller

表4 新型超螺旋二阶滑模转速控制器Table 4 New super twisting second order sliding mode speed controller
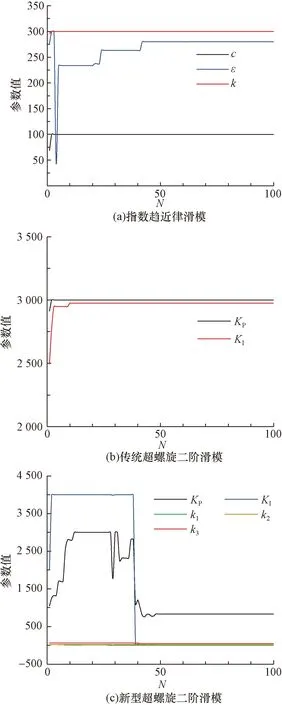
图3 平均参数优化曲线Fig.3 Curves of average parameter optimization
设定PMSM仿真工况如下:仿真时长0.8 s,采样时间1×10-5s。负载转矩TL初始为2 N·m,在0.2 s升至5 N·m,在0.5 s升至7 N·m;期望转速nr*初始为1 000 r/min,在0.3 s升至1 500 r/min,在0.6 s降至1 200 r/min;电机参数Rs、Ψf、Ls在0.4 s分别升至1.5Rs、1.5Ψf、1.5Ls,在0.7 s分别升至2Rs、2Ψf、2Ls。
图4为分别采用指数趋近律滑模、传统超螺旋二阶滑模以及新型超螺旋二阶滑模转速控制器的PMSM转速响应曲线。根据图4(a)可得,在初始时刻、0.3 s与0.6 s,转速因发生阶跃变化而产生超调。其中,对于指数趋近律滑模转速控制器,其转速超调分别约为74.4 %、23.7 %、55.0 %,调节时长分别为0.071、0.077、0.082 s;对于传统超螺旋二阶滑模转速控制器,其转速超调分别约为35.1%、9.5%、11.1%,调节时长分别约为0.037、0.043、0.044 s;对于新型超螺旋二阶滑模转速控制器,其转速超调分别为18.2%、1.1%、6.9%,调节时长分别为0.033、0.023、0.033 s。

图4 PMSM转速响应曲线Fig.4 Curves of PMSM speed response
在0.2、0.5 s与0.4、0.7 s,转速因负载与电机参数变化而产生短暂下降。其中,对于指数趋近律滑模转速控制器,其转速下降幅度分别约为9.3%、4.2%与11.5%、6.0%,恢复时长分别为0.039、0.054 s与0.089、0.085 s;对于传统超螺旋二阶滑模转速控制器,其转速下降幅度分别为0.5%、1.4%与1.4%、3.3%,恢复时长分别为0.026、0.019 s与0.013、0.038 s;对于新型超螺旋二阶滑模转速控制器,其转速下降幅度分别为0.2%、0.8%与0.6%、1.6%,恢复时长分别为0.006、0.018 s与0.008、0.027 s。
在稳态阶段,指数趋近律滑模转速控制器下的转速跟踪误差(实际转速与期望转速间的差值)约为±5 r/min,传统超螺旋二阶滑模转速控制器下的转速跟踪误差为±3 r/min,新型超螺旋二阶滑模转速控制器下的转速跟踪误差为±1 r/min。
对比以上各项指标,结果表明:与指数趋近律相比,采用超螺旋算法设计的滑模转速控制器降低了转速超调,减小了转速在受扰时的下降幅度,缩小了转速稳态跟踪误差。其中,相比传统超螺旋算法,采用新型超螺旋算法设计的滑模转速控制器更进一步地减小了转速超调、转速下降幅度及转速稳态跟踪误差。
根据以上所得结果可知:较之于指数趋近律滑模转速控制器,超螺旋二阶滑模转速控制器明显提高了系统收敛速率、抗电机参数摄动与负载扰动能力,减弱了稳态抖振。其中,与传统超螺旋相比,新型超螺旋二阶滑模转速控制器进一步改善了系统收敛速率、抗内外扰动能力与稳态抖振。
4 结论
从改善传统超螺旋算法收敛速率、控制精度及抖振等多方面出发,设计了一种新型超螺旋算法,提出了一种PMSM新型超螺旋二阶滑模转速控制器,通过在MATLAB/Simulink中与指数趋近律滑模转速控制器和传统超螺旋二阶滑模转速控制器做对比仿真,得到以下结论。
(1)与传统超螺旋算法相比,新型超螺旋算法在收敛性及稳定性等方面得到了改善。
(2)与指数趋近律滑模转速控制器和传统超螺旋二阶滑模转速控制器相比,新型超螺旋二阶滑模转速控制器更进一步地增强PMSM系统的收敛性与抗扰性,抑制了系统抖振。

