某制冰洁净车间气流组织的数值模拟及优化设计

戴志海, 谢东*, 王汉青, 杨红波

(1. 南华大学土木工程学院, 衡阳 421000; 2. 南华大学建筑环境控制技术湖南省工程实验室, 衡阳 421000; 3.中南林业科技大学土木工程学院, 长沙 410004; 4.广州冰泉制冷设备有限责任公司, 广州 511400)

制冰洁净车间中,病毒细菌会附着于空气中的悬浮颗粒物上,再通过依附于冰块进行传播,食品生产过程中暴露在含有超标颗粒污染物的生产环境,这将对人们的卫生安全造成威胁。因此,当局部触发性污染物出现时,快速的去除污染物,减少食品暴露在污染环境中的时间,保证生产环境的洁净度,这有利于保证人民的食品健康安全,也是当前的重要课题。

近年来针对洁净室和室内污染物的研究逐年增多。宋业浩[1]、赵金亮等[2]、韩何[3]分别以国际标准化组织(International Organization for Standardization,ISO)5级和ISO6级洁净室为研究对象,在上送下回、上送单侧下回风和双侧下回风3种回风方式下进行数值模拟,以流线平行度和风速为指标,指出上送下回的气流优于上送测回;在ISO6级洁净室内,上送单侧回形式,会出现明显涡流,而上送双侧回形式,涡流不明显,气流效果更佳;在ISO5级洁净室内,单侧回形式无法完全达到单向流的要求,而双侧回形式的气流均匀性好,完全能达到单向流的要求。周俊杰等[4]以垂直单向流洁净室为研究对象,以流线平行度为指标,通过模拟分析得出FFU布置率为80%时满足垂直单向流洁净室的设计要求。郭雨洁等[5]和李晓敏等[6]分别对地下超市和地铁站内的气流组织进行数值模拟,分析了速度场和温度场,得出地下超市和地铁站的速度场和温度场的分布规律。综上可知,上述研究仅关注速度场,未考虑颗粒物分布。刘莉等[7]通过CFD对室内颗粒污染物的分布情况进行模拟分析,指出地面污染物浓度过高时会对整个洁净室产生影响。李云广等[8]针对孔板送风的非单向流流洁净室,对15～70次不同换气次数条件下污染物扩散进行数值模拟分析,得出换气次数为55次时,洁净室排污效果最佳,继续增大换气次数对室内污染物分布状况没有明显改善。刘瓅等[9]以非单向流洁净室研究末端形式、回风口位置、换气次数3个因素对室内颗粒污染物的影响,结果表明,回风口应该优先布置于房间角落,有利于提高房间平均洁净度;末端形式时影响局部颗粒物浓度的显著性因素,换气次数是影响室内平均浓度的显著性因素。

大量研究表明,CFD(computational fluid dynamics)方法是对洁净室探究的有效工具,对于单向流和以散流器为送风口的传统的上送下回的形式已有丰富的研究,但对于特殊空调系统的研究尚鲜见报道。鉴于此,以某低温制冰洁净车间为研究对象,为了探究洁净风柜不同的布置方式、送风角度、换气次数对污染物排除速率和温度均匀性的影响,建立三维物理模型进行数值模拟,选生产区域为需要优化的微环境[10],通过对比模拟,选取最佳布置方案,再通过单因素模式实验解析不同影响因素对污染物去除速率和温度均匀性的影响,寻求污染物排除速率和温度均匀性的平衡,最终确定最优的排布方案和运行工况,实现对洁净车间生产区域内微环境的优化,提高微环境内污染物的去除速率和温度均匀性,为后续洁净车间的运行设计和研究提供了模型参考和理论支持。

1 模型建立

1.1 几何模型的建立

对洁净车间内部进行气流组织模拟分析,该洁净车间为低温十万级洁净车间,设计温度为-10 ℃,车间内制冷系统与洁净系统相互独立,冷源为车内顶部吊顶冷风机,洁净风柜(FFU)对室内空气进行循环过滤,以此实现对车间内温度场和污染物浓度的控制。

以 1∶1 的车间尺寸建立数字模型,车间几何模型如图1所示,车间内各物品尺寸如表1所示。

表1 车间几何模型参数Table 1 Geometric model parameters of workshop

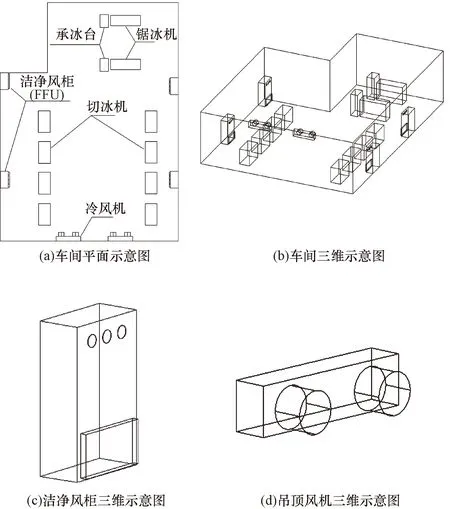
图1 车间模型示意图Fig.1 Schematic diagram of the workshop model

1.2 控制方程

采用连续相气流流场和颗粒相耦合的方法进行数值模拟,气流场采用室内气流流场效果较好的Realizablek-ε湍流模型计算,计算公式为

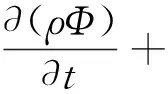
(1)

式(1)中:ρ为气体密度;Φ通用变量,可表示速率分量u、v、w和热力学温度T等求解变量;t为时间;为梯度;K为广义源项。

对颗粒相的计算采用离散相颗粒模型DPM(discrete phase model),该方法是在拉格朗日法的基础上建立的,因此可以追踪颗粒的运动轨迹,可以计算两相耦合和单相耦合问题。

1.3 边界条件与喷口模型简化

1.3.1 喷口模型简化

本次模拟研究为了使模拟结果更加精确,将车间模型和洁净风柜的球形喷口模型拆分成两个独立的模型,由于风柜内部风管到各个喷口的距离一直,故将风管段进行了简化缩短。

球形喷口由执行机构、球形装饰圈、喷口及壳体组成,结构示意图如图2所示。本次模拟研究为了便于生成高质量的网格,将球形喷口的球星装饰圈和壳体忽略,仅保留了流体区域,得到的球形喷口简化模型的喉部曲率与实际球形喷口一致,球形喷口简化结构如图3所示。

图2 喷口结构示意图Fig.2 Schematic diagram of nozzle structure

图3 简化喷口模型Fig.3 Simplified nozzle model

受球形喷口结构和风管阻力的影响,喷口出流断面的流速并不均匀,故将球形喷口边界参数导入后,明显提高了本次模拟的准确性。

1.3.2 边界条件设置参数汇总

本次模拟研究中,吊顶冷风机的送风口、洁净风柜的送风口均采用流速入口,而由于压力入口和自由出流无法同时使用,又要保证风口流量的准确性,故将吊顶冷风机的回风口和洁净风柜的吸风口设为速度出口。

洁净风柜的净化率为99.99%,故近似认为洁净风柜送风认为是无尘新风;车间内墙面全为保温钢板,故将其是为绝热表面。

气溶胶散发源将其布置于生产区域内(x=9 m,y=8 m,z=1.2 m),其物性参数为:直径为0.5～10 μm,平均粒径为1.0 μm,强度为1×10-4kg/s,释放时长为1 s。边界条件具体参数设置如表2所示。

表2 边界条件设置参数Table 2 Setting parameters of boundary conditions

1.4 网格无关性验证

在有限的计算资源前提下保证计算速率和准确性,建立了网格数分别为9×105、17×105、25×105、35×105和55×105的网格进行网格无关性验证。在流场中心取一条垂直直线(x=8 m,y=15 m),得到其稳态状态下的速率分布,如图4所示。

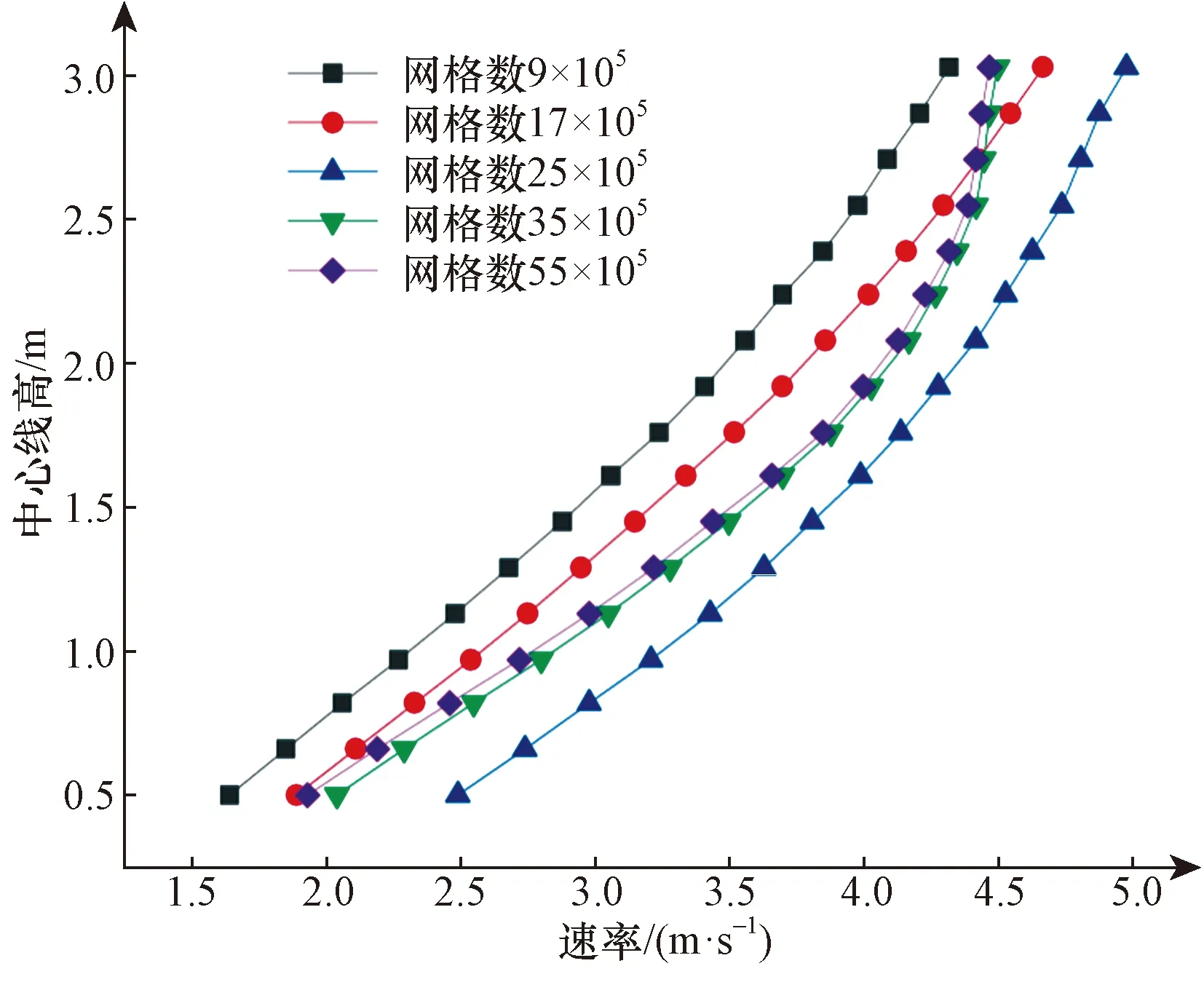
图4 5种不同网格数量下空间的中心线高变化速率分布Fig.4 Distribution of high change rate of center line in five different grid number Spaces

从图4可以看出,在5种网格空间中,网格数为9×105、17×105和25×105的速率分布与35×105的相比有较大的差距,但网格数为35×105的速率分布与55×105的速率分布结果相比差距很小,最大偏差为2.1%。因此网格数为35×105的网格敏感性已经达标,最终选择35×105网格数作为全局网格划分方案的参数。

2 评价指标

(1)残留率[11-12]。洁净车间对局部触发的气溶胶污染物的短时间内的去除速率,设定1 s内由局部触发的气溶胶污染物,在1 min内气溶胶污染物在车间内的残留率的变化情况。

(2)温度均匀性[13]。将洁净车间分为两个矩形区域,将布置了切冰机和洁净风柜的矩形区域定为生产区,而另一个矩形区域为非生产区;生产区域内的温度稳定性对于产品质量的影响非常大,通过主要工作区域内的1 m水平面上均匀选取60个样本点的温度值的标准差来评价生产区域内的温度均匀性。

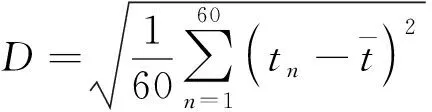
(2)

3 洁净车间通风布置方案研究

3.1 布置方案拟定

所研究的对象为实际运行的制冰车间,冷风机管道位置固定,只考虑对车间内的4个洁净风柜的布置,选取3种布置方式作为仿真对象,将其拟定为3个布置方案,3种布置方案的几何物理模型如图5所示。

3.2 模拟结果与分析

3.2.1 车间的颗粒物弥散分析

洁净车间内颗粒从污染源散发出来后60 s内的颗粒弥散过程如图6所示。当颗粒喷出5 s时,颗粒仅随气流运动到污染源下方,扩散性不强,颗粒团处于聚集状态。当颗粒喷出10 s时,小部分粒子滞留于散发源附近,但绝大多数颗粒分成三股粒子流,分别从切冰机的空隙间穿过并流入侧方的两个洁净风柜的回风口。当颗粒喷出15 s时,大多数的颗粒随空气流入洁净风柜的回风口被捕捉过滤,剩余颗粒随着气流向洁净室上方运动。当颗粒喷出20 s之后,颗粒物随着室内流场扩散到整个洁净室,颗粒物浓度随时间匀速下降。

不同颜色散点代表颗粒物滞留时间图6 不同时刻颗粒物弥散图Fig.6 Dispersion diagram of particles at different times

图7为颗粒物残留率随时间的变化关系。3种排布方案中,方案A在60 s时的残留率最低,方案A在60 s时的残留率为5.7%,其后依次是方案B、方案C,残留率依次为19.5%、65.4%。随着颗粒物的释放,在t=1 s时颗粒物残留率浓度达到峰值,并且会在峰值维持一段时间。

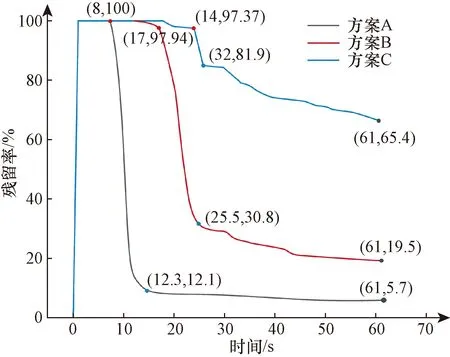
图7 不同排布方案60 s内颗粒残留率Fig.7 Particle residual rate within 60 s in different arrangement schemes

60 s的时间内,3种排布方案的颗粒物的残留率均存在一段陡降区间,这是由于颗粒物从释放源释放出来后处于一种聚团状态,初始时段大量颗粒物随着气流移动进行小规模的扩散,又由于洁净风柜的回风口位于洁净室的下方区域,洁净室下方空间的气流主要是流向洁净风柜的回风口,故一大部分颗粒在释放后就在较短时间内被洁净风柜捕集过滤,这一现象在文中定义为“一次去除”。方案A的颗粒物“一次去除”发生的时间最短,“一次去除”时间点为8 s,方案B、方案C的“一次去除”时间点分别为17、24 s。方案A、方案B、方案C颗粒物残留率发生“一次去除”后的残留率分别为12.1%、30.8%、84.1%。洁净风柜的回风口位置对于“一次去除”起到至关重要的影响,颗粒物发生“一次去除”的时间点越早,颗粒物扩散的范围就越小,“一次去除”的效率越高。

3.2.2 温度场分析

图8为不同排布方案生产区域z=1.2 m水平面上的平局温度和温度标准差。可以看出,3种排布方案在相同能耗条件下,方案A、方案B、方案C的平均温度分别为263.53、263.92、263.63 K,其中方案A的平均温度最低;方案A、方案B、方案C的温度标准差分别为0.244、0.252、0.343,方案A的温度标准差是最小。

图8 不同排布方案生产区域z=1.2 m的平均温度和温度标准差Fig.8 Average temperature and standard deviation of z=1.2 m in production area with different arrangement schemes

3.2.3 布置方案选定

综合上述结果分析,选择方案A为最终布置方案。从颗粒物残留率角度,方案A对生产区域内随机触发颗粒物的“一次去除”效率和60 s内的去除效率均是最高,“一次去除”效率高出其余方案18.7%,60 s内的去除效率高出其余方案13.8%;从温度场的角度,方案A的平均温度和温度标准差最低,平均温度和温度标准差相较于其余方案降低了0.1 K和0.01,工作区域的温度最低,温度均匀性最好。在相同能耗的条件下,方案A对生产区域内随机触发的污染物去除速率最快,降低了冰块生产过程中暴露在颗粒污染物下的概率;方案A生产区域内的平均温度更低,可降低供冷能耗,节约运行成本;方案A的温度均匀性更优越,对食品生产质量有显著提升。

4 不同送风工况工作特性研究

4.1 单因素模拟

通过改变洁净风柜送风角度和换气次数在洁净室模型内进行单因素模拟分析,模拟工况如表3所示。

表3 模拟方案Table 3 Simulation scheme

4.2 各因素对颗粒物残留率的影响

进行单因素模拟,得到各因素中颗粒物残留率随时间变化的关系如图9所示。可以看出,出口送风角度对颗粒物残留率的影响非常大,随着出口送风角度的增加,颗粒物的残留率呈现一种先减后增趋势,当出口角度达到45°时颗粒物残留率最低,“一次去除”效率为81.9%,颗粒物残留率为5.7%;随着换气次数的增加颗粒物残留率呈现不断降低的趋势,当换气次数为30次/h时,颗粒物残留率最低,“一次去除”效率为99.36%,颗粒物残留率为0.43%。因此在单因素实验中,选择送风角度45°,换气次数30次/h作为颗粒物去除速率的最优组合。

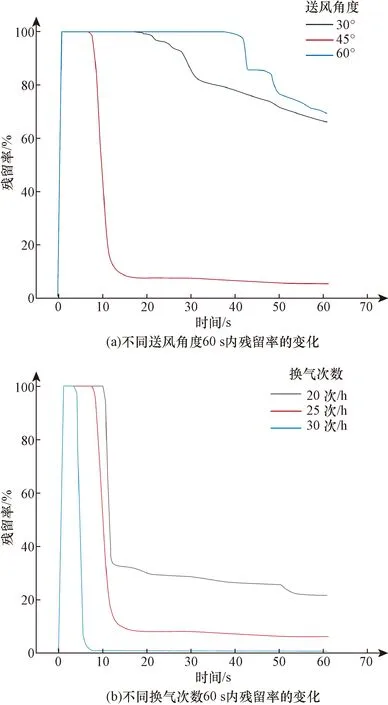
图9 各因素下颗粒物残留率60 s内的变化Fig.9 Variation of particulate matter residual rate within 60 s under various factors

4.3 各因素对温度均匀性的影响

通过单因素模拟,对各因素下生产区域z=1 m水平面上均匀选取60个温度值,结果如图10所示。由图10模拟结果可知:随着出口送风角度的增大,生产区域内的平均温度越小,且编号1～20的测点的温度值绝大部分是高于平局温度,各测点的温度波动性变化不大;随着换气次数的在增大,生产区域内的平均温度越小,当换气次数为20次/h和30次/h是,各测点的温度波动性显然小于换气次数为25次/h时的情况。

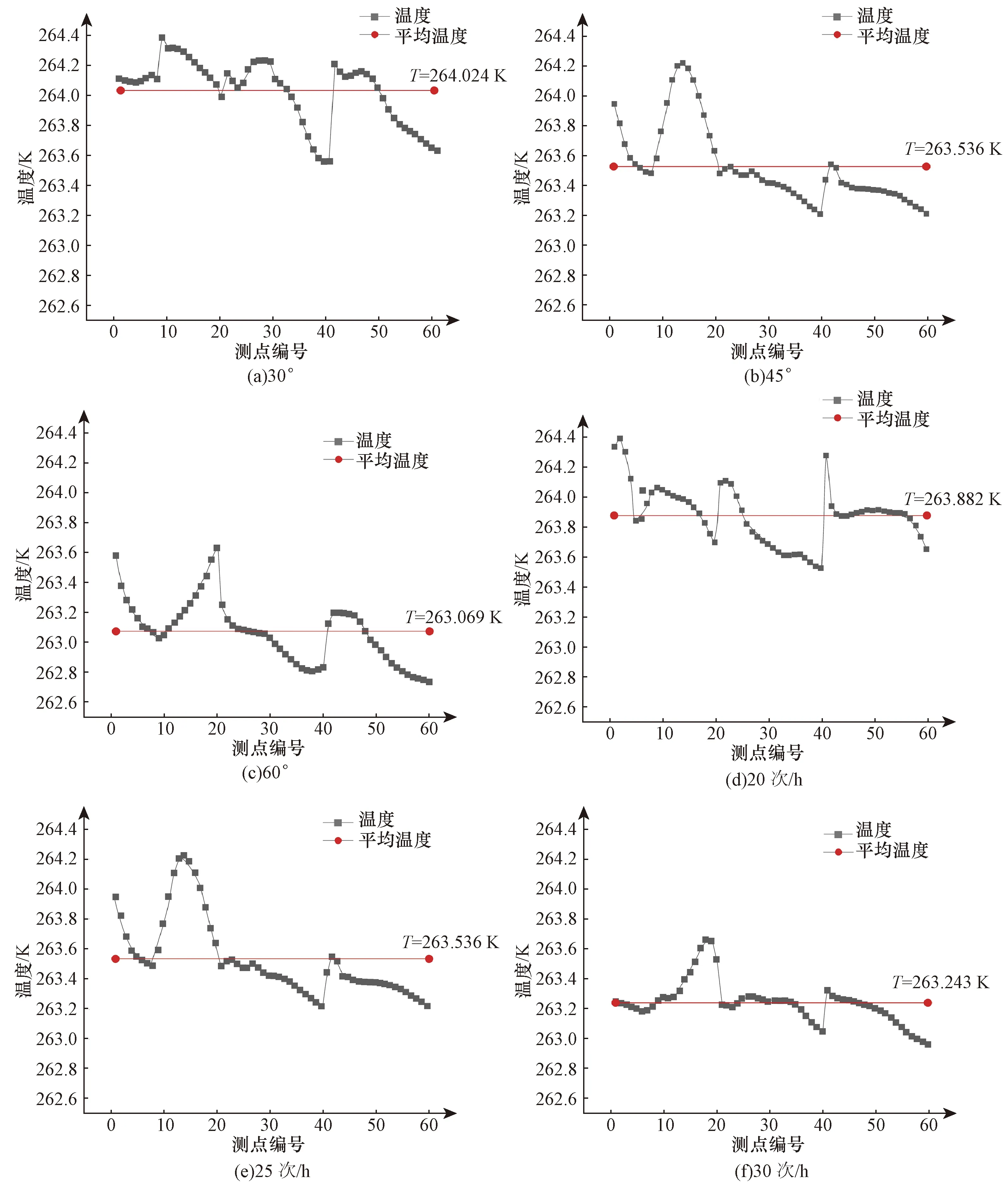
图10 各因素工况下各个测点的温度分布Fig.10 Temperature distribution of each measuring point under various factor working condition

编号21～60的温度值绝大部分是低于平均温度,这是由于编号1～20测点位于生产区域靠左侧的位置,生产区域左侧上方为固体墙面,而编号21～60测点位于生产区域的中间和右侧,该区域上方和非生产区域相通,左侧区域的设备产热扩散速度相对于中间和右侧的区域更慢,所以造成了左侧区域温度较高,右侧区域温度较低的现象。

单因素模拟得到各因素下相对湿度标准差如图11所示。可以看出,随着出口送风角度的增大,温度标准差先增大后减小,当出口送风角度为60°时,温度标准差为0.209,生产区域内温度最均匀;随着换气次数的增加温度标准差先增加后减小,当换气次数为20次/h时,温度标准差为0.142,生产区域内温度最均匀。因此选择送风角度60°,换气次数20次/h作为单因素实验温度均匀性最优组合。

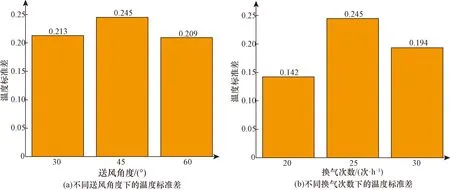
图11 各因素下的温度标准差Fig.11 Standard deviation of temperature under each factor

4.4 因素交互性分析与方案选定

通过单因素分析分别得出了各因素对颗粒物去除速率和温度均匀性的影响趋势,但是从单因素分析得出的对于去除速率的最优组合和温度均匀性的最优组合各不相同,这是因为单因素分析需要假定各因素间没有交互作用,既单因素结果并不是很精准的优化组合。因此,为寻求去除速率和温度均匀性两者的平衡,将剩余所有组合进行模拟对比(因为因素数为2,无需进行正交实验),表4为所有组合模拟结果,其中,原运行工况组合为送风角度45°,换气次数20次/h,表4中变化率和差值是与原工况组合参数进行对比。

表4 模拟结果Table 4 Simulation results

综上分析可知:各因素对于颗粒物去除速率的影响程度:送风角度>换气次数;各因素对于温度均匀性的影响程度:换气次数>送风角度。综合考虑去除速率和温度均匀性,选取送风角度45°,换气次数30次/h为优化组合;相较于原方案,颗粒物在60 s内的去除率提高了5.3%,温度标准差降低了0.05,温度均匀性提高了22.3%,该方案在去除速率和温度均匀性上均得到了优化。

5 结论

(1)选定方案A为最佳布置方案,方案A对生产区域内随机触发颗粒物“一次去除”效率为87.9%,高出其余方案18.7%,60 s内的去除效率为5.7%,高出其余方案13.8%,快速排除污染物的能力最强;平均温度和温度标准差相较于其余方案分别降低了0.1 K和0.01,工作区域的温度最低,温度均匀性最好。

(2)“一次去除”效率对于洁净室内颗粒物的快速排除有着非常重要的作用,“一次去除”发生的时间越早,“一次去除”效率越高,将吸风口布置于重要洁净区域有利于局部触发性污染物的快速排除。

(3)利用单因素实验和对比实验寻求污染物去除速率和温度均匀性的平衡。两个实验因素对于污染物去除速率的影响程度为:送风角度>换气次数;两个实验因素对于温度均匀性的影响程度为:换气次数>送风角度。

(4)当送风角度为45°,换气次数为30次/h时污染物去除速率和温度均匀性均得到优化,较于原方案,颗粒物的去除率提高了5.3%,温度标准差降低了0.05,温度均匀性提高了22.3%。