新型灌浆套筒凸肋深度力学性能研究

虞小平, 梁都*, 虞爱平, 张明浩

(1.桂林理工大学南宁分校土木与测绘工程系, 崇左 532100; 2.桂林理工大学土木与建筑工程学院, 桂林 541004)

为推进建筑产业化快速升级,针对灌浆套筒连接技术学者们开展了大量研究。苗吉军等[1]从灌浆套筒自身组分即灌浆料、套筒、连接钢筋出发,总结了不同因素对试件力学性能影响。高强[2]通过试验数据、理论分析及数值模拟结果,提出了该类新型灌浆套筒接头的设计方法。马福金[3]给出新型连接接头的力学模型,推导出连接接头搭接长度的计算公式,提出套筒及搭接长度相关构造要求。Zhao等[4-5]研究了高温、静载和疲劳荷载作用下预应力灌浆套筒连接的延性、极限荷载及吸能情况。11个连接试样置于高温中并施加不同级荷载,观察其变形。最后发现随着管外和管内温差的增加,连接件的极限荷载几乎成线性趋势下降。朱万旭等[6]介绍了灌浆套筒的组成、原理和套筒尺寸,对排浆管和灌浆管的位置、拼接进行了详细的研究。鲜艾珂[7]通过ABAQUS有限元软件对钢筋灌浆套筒连接构件进行了单向拉伸、高应力和大变形反复拉压数值模拟分析,取得了一定成果。郑永峰等[8]分析了套筒的连接性能,得到当钢筋锚固长度是连接钢筋直径的6.9～7.5倍时,新型灌浆套筒接头的单向拉伸强度满足《钢筋机械连接技术规程》(JGJ 107—2010)Ⅰ级接头强度和变形性能的要求。黄远等[9]通过半灌浆套筒的单向拉伸受力性能,对14个试件进行试验,得到当为钢筋拉断破坏时,连接钢筋偏心对灌浆套筒连接构件的承载力影响极小,钢筋的螺纹形状、套筒的质量和肋深对半灌浆套筒连接件的承载力影响较大。

综上可知,前人对灌浆套筒连接的研究较少,特别是新型灌浆套筒在连接的施工技术、质量控制以及己有套筒产品的连接接头性能检验方面。为顺应工业产业化节能、降低成本、减少污染的要求,现结合黏结滑移理论,在考虑新型灌浆套筒连接件间的黏结滑移,包括径向应力、环向应力、径向位移及连接件接触表面界面压应力情况下,对新型灌浆套筒的凸肋深度力学性能进行分析。

1 研究内容

以自制直径为32 mm的HRB400钢筋,作为新型灌浆套筒连接件为研究对象,采用理论分析、数值模拟及试验研究相结合的方法,保持钢筋和灌浆料各性能参数不变情况下,对该自制灌浆套筒考虑套筒的壁厚参数影响下的力学性能开展分析和研究,为预制装配式建筑的推广及应用提供参考数据。具体内容如下。

(1)采用两种内径相同的冷轧套筒,分为A、B两组灌浆套筒连接件,通过单向拉伸试验,确定连接件的破坏形态,分析其受力机理。

(2)利用套筒凸肋深度受力模型,基于弹性力学理论得出的黏结滑移参数代入ABAQUS建立的新型灌浆套筒数值模型中,在单向拉伸作用下,将模型计算得到的数值结果与试验结果通过荷载—位移曲线做对比,分析连接件受力机理,验证有限元软件所建模型的合理性。

(3)以套筒凸肋深度为变量,用壁厚为5 mm,肋间距为30 mm,凸肋深度为2、2.5、3、3.5、4 mm的无缝钢管。直径为32 mm的HRB400钢筋,厚度为12.5 mm的灌浆料组成的新型灌浆套筒,建立5组不同套筒凸肋深度的计算模型。利用有限元软件模拟其单向拉伸,并将模拟计算得到的应力—应变曲线、传力机制和极限承载力结果进行对比分析,找出凸肋深度最优套筒。

(4)根据研究成果得出适用于直径为32 mm的HRB400钢筋新型灌浆套筒构造尺寸,并验证新型灌浆套筒的可行性,对下一步的研究工作提出针对性的建议。

2 单向拉伸试验

在试验的基础上,采用ABAQUS有限元分析软件,建立直径为32 mm 的HRB400钢筋灌浆套筒连接件数值计算与分析模型,对其在单向拉伸荷载作用下进行数值模拟研究,确定连接件破坏模式和趋势,找出钢筋、灌浆料和新型套筒的应力、应变分布规律,并对三者之间的受力状态和传力进行修正,然后将模拟计算结果与试验结果进行对比分析,验证模型的可靠性。新型灌浆套筒设备如图1所示。

2.1 室内试验

试验用灌浆套筒分为A、B两组,每组3个试件,试件的构造及尺寸参数如图2和表1所示。

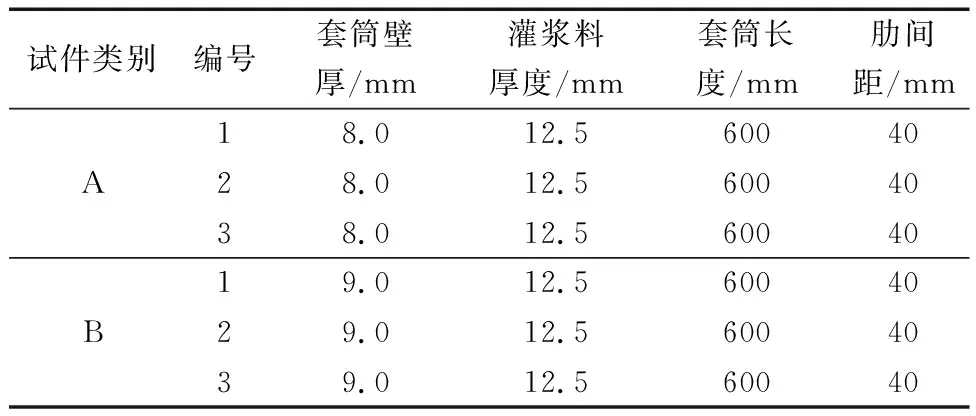
表1 试件尺寸Table 1 Specimen size

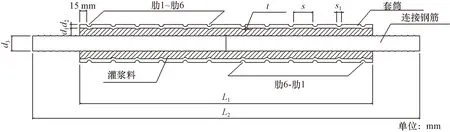
d1为灌浆料厚度;d2为套筒壁厚;t为肋深;s为肋间距;s1为肋宽;L1为套筒长度;L2为钢筋长度;连接钢筋采用HRB400,公称直径d3为32 mm图2 新型灌浆套筒构造图Fig.2 Construction diagram of new grouting sleeve

新型灌浆套筒试件如图3所示,灌浆前先将一段连接钢筋插入木架底部的小孔固定住,分别插入套筒和另一段连接钢筋后进行灌浆,钢筋对中较好。

图3 新型灌浆套筒试件Fig.3 Specimen of new grouting sleeve

由于忽略灌浆料内部缺陷,所以灌浆料直接从套筒端口灌入,在灌浆料内部气泡冒出后及时补浆。为防止套筒底部出现漏浆现象,在筒口边缘涂泡沫胶封口。灌注灌浆料后,试件需要在养护室养护10 d。

2.1.1 加载方式

根据《钢筋机械连接技术规程》(JGJ 107—2010)规范要求,将连接件在万能试验机上进行静载拉伸试验,试验机最大量程和加载速率分别为1 000 kN和2 MPa/s,按照试验加载方案顺序加载,当加载至0.6倍的钢筋屈服强度后再卸载至0,接着加载至试件完全破坏,试验过程中的荷载及其夹具之间的位移均由试验机自动记录,如图4所示。

图4 万能试验机加载装置Fig.4 Loading device of universal testing machine

2.1.2 结果与分析

通过试验可知,试件的破坏形态为钢筋拉断破坏和灌浆料拔出破坏,试件破坏形态及力-变形曲线如图5、图6所示。

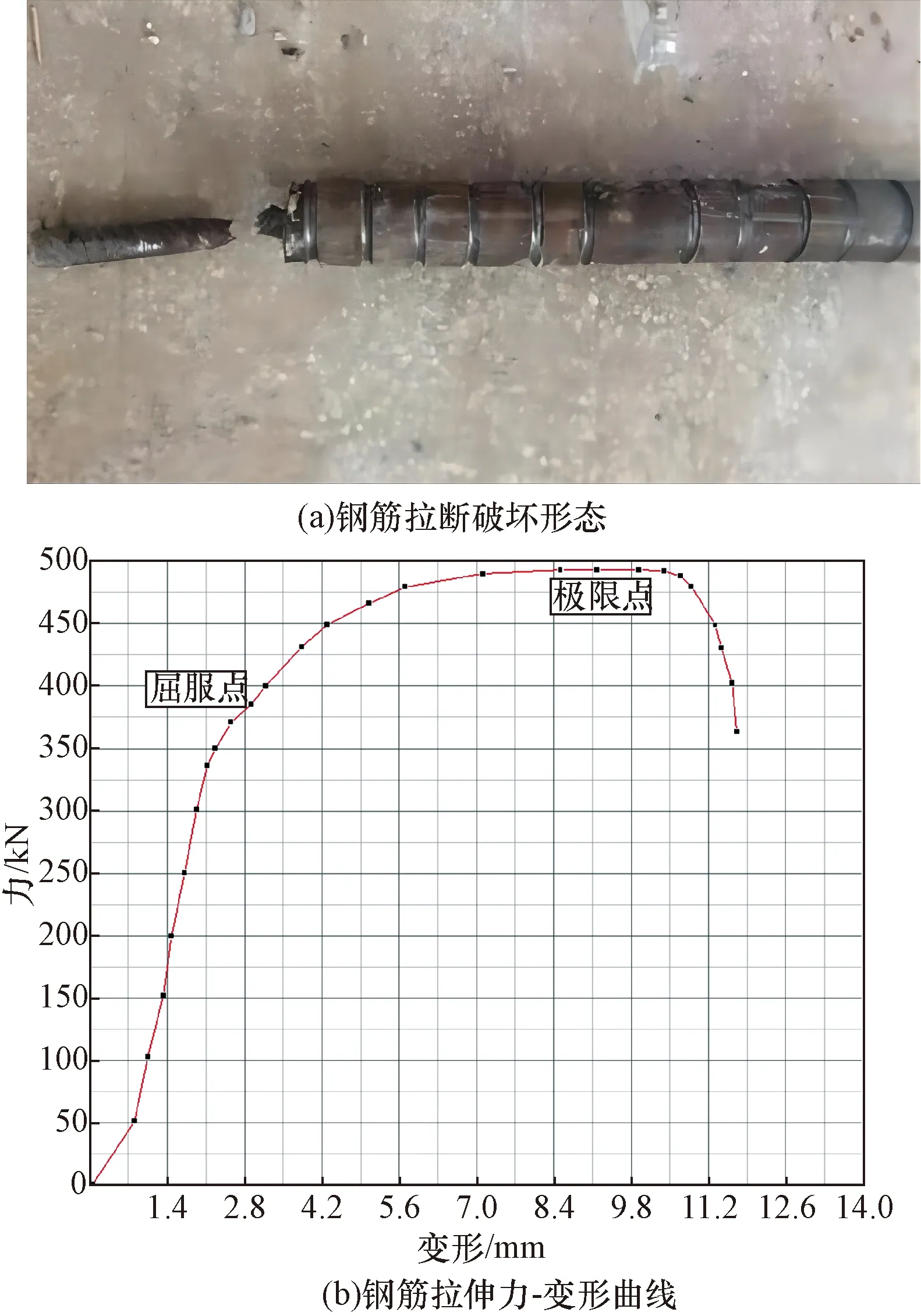
图5 钢筋拉断破坏形态与力-变形曲线Fig.5 Tensile failure mode and force-deformation curve of reinforcement

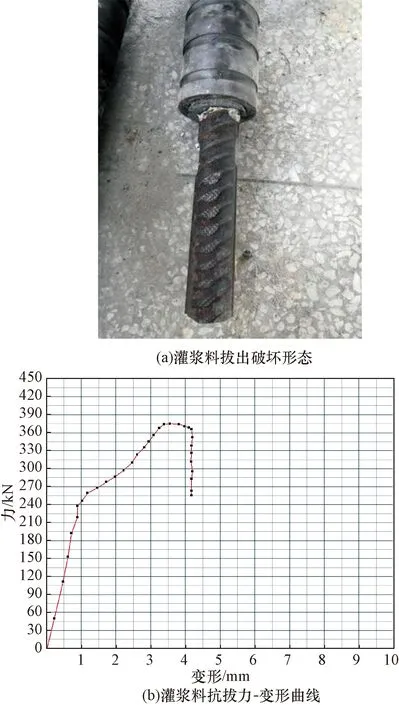
图6 灌浆料拔出破坏形态与力-变形曲线Fig.6 Pull-out failure pattern and force-deformation curve of grouting material

(1)钢筋拉断破坏。端部的灌浆料先被劈裂损坏,然后钢筋出现颈缩后被拉断,其最大承载力为490 kN。力-变形曲线出现两个上升段和一个微小的屈服平台,屈服点在375 kN,满足大于1.15倍钢筋屈服强度的性能指标,且屈服强度和极限强度均满足规范要求。进入强化阶段后,试件位移随力变化幅度较小,说明此时已进入强化阶段,套筒的约束能力仍然很好。受力超过475 kN后,随着位移增大,力增加幅度较小,直至破坏。

(2)灌浆料拔出破坏过程。随着荷载增大,灌浆料和钢筋被缓慢从套筒中拔出,同时钢筋出现微小的颈缩现象,连接件最大承载力为365 kN,夹具间最大位移为4.2 mm,其力-变形曲线与钢筋拉断破坏试件的曲线类似,第一阶段属于弹性阶段,力-变形曲线呈直线上升趋势,此阶段试件刚度较大,抵御外部变形能力较强;第二阶段属于钢筋接头屈服阶段,屈服力为310 kN,较钢筋拉断破坏模式值低;随着荷载持续增加,钢筋第三阶段是强化阶段,该阶段持续时间很短,当极限承载力达到365 kN后,力-变形曲线开始出现下降,最后钢筋及灌浆料被拔出,试件停止工作。

2.2 ABAQUS数值分析

ABAQUS/Explicit[10]是一种适用于高阶非线性连续介质和结构分析的有限元求解器。它对于非线性瞬态现象和准静态仿真,特别是瞬态动力学仿真具有很好的适用性。在相应产品的设计环境中,能有效地解决非线性问题,包括接触和许多准静态问题。

通过黏结滑移理论,考虑灌浆套筒连接件间的黏结滑移,包括径向应力、环向应力、径向位移[11-13]及连接件接触表面界面压应力情况下[14],数值模型计算得到的应力分布云图,如图7～图12所示。

图7 连接件接头Mises应力分布云图Fig.7 Mises stress distribution cloud diagram of connectors

图7为两种连接件接头破坏模式的Mises应力分布云图,可知接头破坏趋势基本一致,钢筋拉断时有明显的颈缩现象,连接件接头钢筋最大Mises应力为600.3 MPa,已超过钢筋极限抗拉强度550 MPa,表明此时钢筋已经被拉断;灌浆料被拔出这种破坏模式,由于套筒与灌浆料表面黏结应力较小,在拉伸过程中钢筋与灌浆料一同被拔出,此时Mises应力最大值为352 MPa,表明钢筋并未达到屈服连接件就已经停止了工作。

由图8可知,钢筋拉断和灌浆料拔出这两种破坏模式的连接件轴向应力变化总体上相差不大,轴向应力均为拉应力,由连接件轴向应力分布云图对比分析可知,钢筋拉断的轴向应力为477.6 MPa,灌浆料被拔出时的轴向应力为482.7 MPa,表明灌浆料被拔出过程中的轴向应力较钢筋拉断时稍大一些。

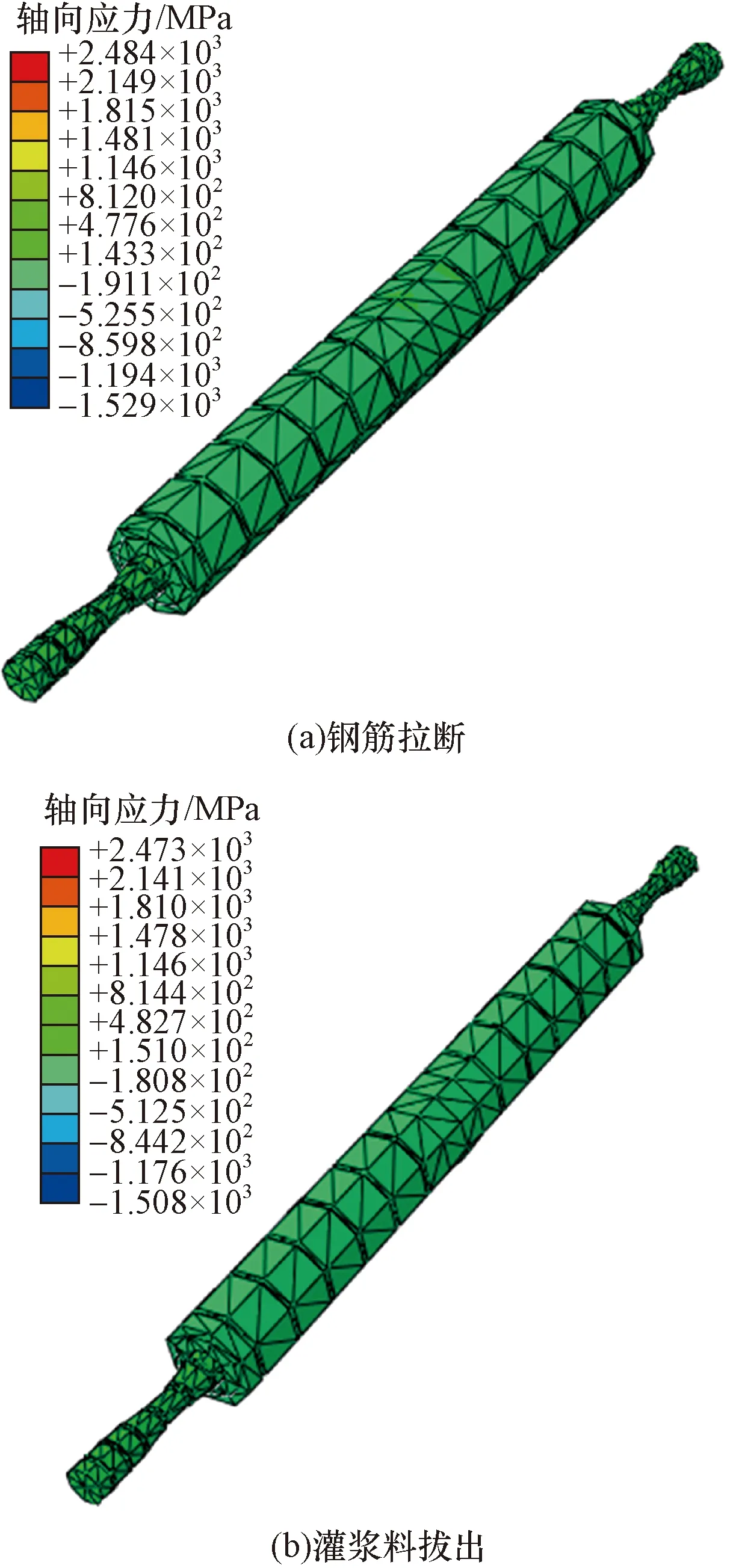
图8 连接件轴向应力分布云图Fig.8 Axial stress distribution cloud diagram of connectors

由图9所示的套筒Mises应力分布云图可知,钢筋被拔断的套筒在其端部出现一处极大Mises应力集中,最大值为153.3 MPa,套筒中部Mises应力最大值为130.9 MPa,远小于其最大屈服强度值380 MPa和最大抗拉强度550 MPa,表明套筒仍具有很大的安全储备空间。除此之外,其他部位所受轴向应力较小;灌浆料被拔出的轴向应力最大数值为151.7 MPa,并集中在套筒中部,其他部位所受轴向应力较小,套筒端部所受轴向应力最小。从图10可以看出,钢筋被拉断时,套筒中部第一主应力受力分布较复杂,其值在127.9～148.1 MPa浮动,表明钢筋在受拉过程中,套筒中部受其影响最大,属于较容易发生黏结破坏的部位;灌浆料拔出破坏时第一主应力最大值集中在套筒中部,与钢筋被拔断破坏不同的是,灌浆料拔出破坏的第一主应力最大值在套筒中部分布较均匀,并没有钢筋拉断时套筒中部出现“斑马”现象,最大值为152.5 MPa,分析可知,钢筋拉断破坏的第一主应力值稍低于灌浆料拔出破坏的第一主应力值。

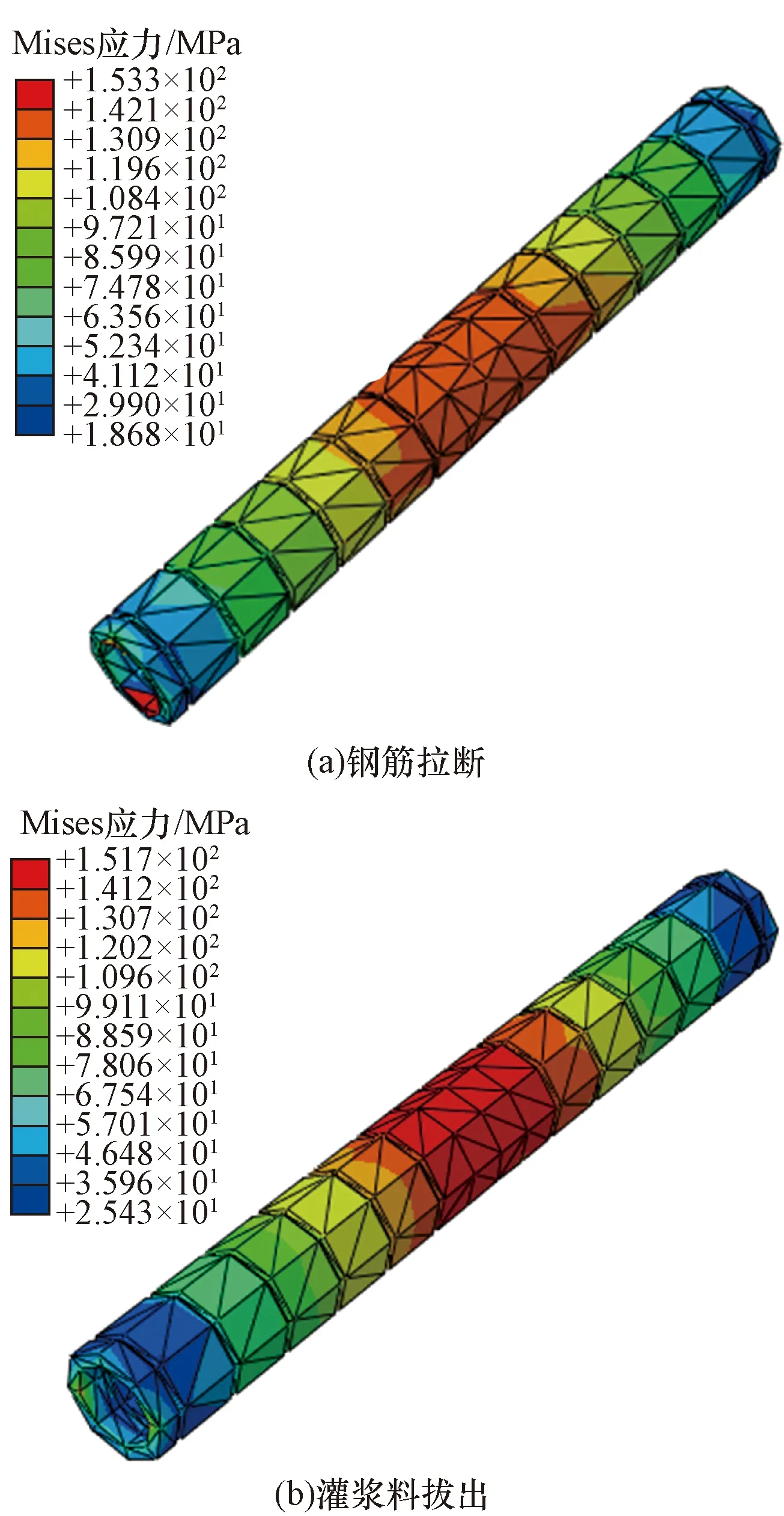
图9 套筒Mises应力分布云图Fig.9 Nephogram of telescopic mises stress distribution

图10 套筒第一主应力分布云图Fig.10 Stress distribution cloud diagram of sleeve Mises

从图11、图12可以看出,灌浆料第三主应力和轴向应力分布大体上为压应力,钢筋拉断与灌浆料被拔出的灌浆料第三主应力最大值均发生在与套筒接触的第一个肋附近,分别为98.5、93.8 MPa,且钢筋拉断时灌浆料的第三主应力值较灌浆料拔出时的稍大,由图11可知,两种破坏模式的灌浆料中部第三主应力为拉应力,其值在9.6～11.5 MPa变化。灌浆料轴向应力分布与其第三主应力分布类似,区别在于,灌浆料轴向应力分布的两种破坏模式灌浆料轴向应力分布整体均为压应力,这是由于钢筋在拉伸过程中套筒对其切向应力约束造成的,轴向应力最大值分别为28.1、26.2 MPa。由上述分析可知:钢筋拉断破坏的灌浆料第三主应力值是灌浆料拔出破坏时的28.5%,钢筋拉断破坏的灌浆料轴向应力值是灌浆料拔出破坏时的27.9%。

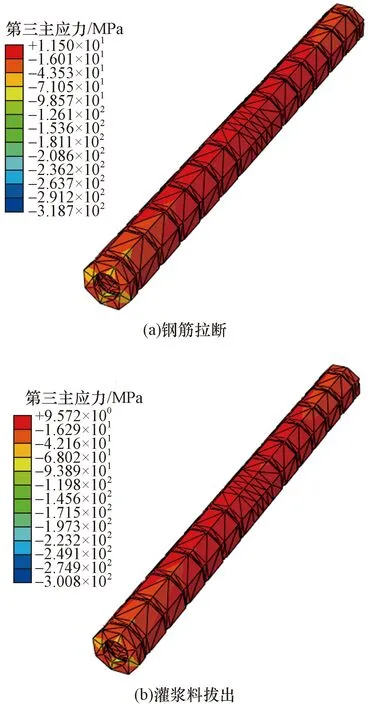
图11 灌浆料第三主应力分布云图Fig.11 Distribution cloud diagram of the third principal stress of grouting material

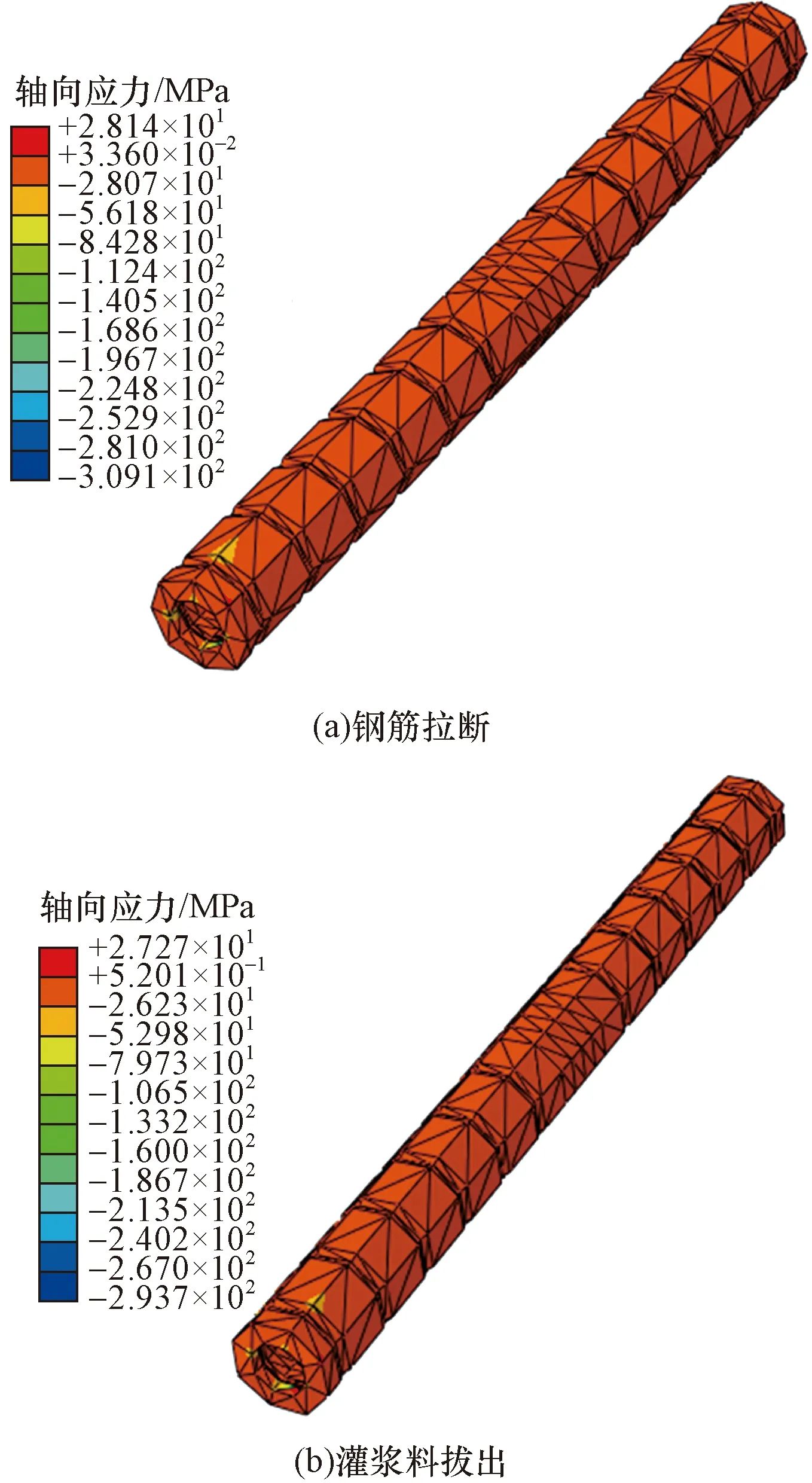
图12 灌浆料轴向应力分布云图Fig.12 Axial stress distribution cloud diagram of grouting material

2.3 模拟结果与试验结果对比分析

试件受拉产生的钢筋拉断和灌浆料被拔出的荷载—位移曲线形状跟模拟结果与试验结果吻合良好,并且采用ABAQUS有限元分析出来的荷载-位移曲线与试验的荷载-位移曲线均有明显的屈服平台,如图13所示。

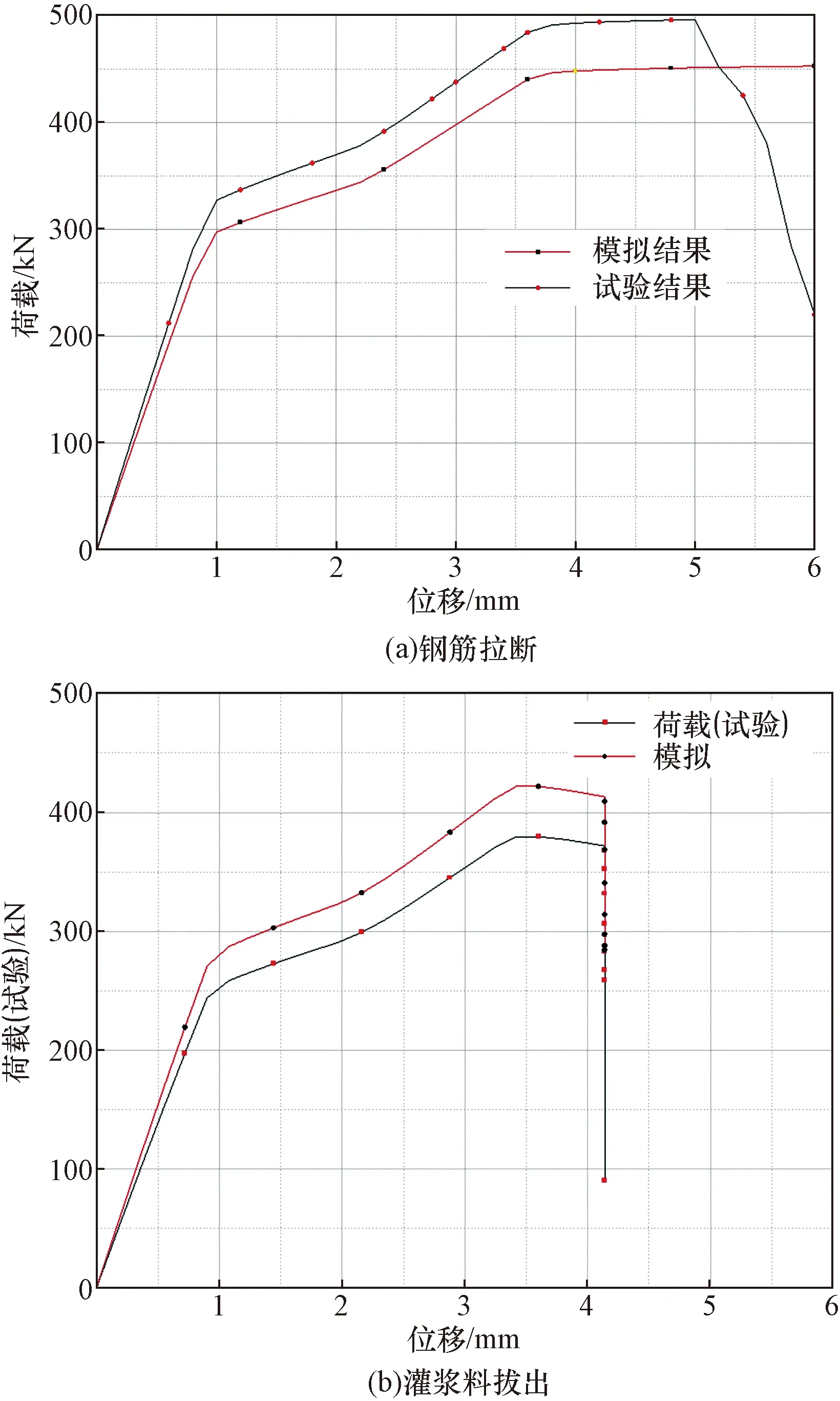
图13 模拟与试验荷载-位移曲线Fig.13 Simulated and tested load-displacement curves

从图13中可以看出,钢筋屈服前,有限元的荷载-位移曲线与试验的荷载-位移曲线在弹性阶段吻合较好;说明此阶段钢筋的刚度较大,而在钢筋屈服后,由于钢筋在本构关系中采用的是理想化的双折线模型分析,最后强化为一条直线,因此,在钢筋进入强化阶段后,有限元的荷载-位移曲线与试验的荷载-位移曲线稍有些偏差,且模拟结果稍低于试验结果,在偏差允许的范围内,其结果仍然吻合较好,说明有限元所建立的模型正确。

对比钢筋拉断时模拟与试验结果的极限荷载和位移可知,连接件接头有限元分析的极限承载力为450 kN时达到钢筋的极限抗拉强度,最大位移为5.8 mm,由于软件本身局限性,钢筋本构关系采用的是双折线模型分析,导致在有限元分析中并没有体现出钢筋的颈缩阶段,而在试验过程中,钢筋颈缩造成的位移增长量较大,最大位移为5.3 mm,极限承载力为490 kN。通过分析发现模拟承载力较试验承载力偏小,原因主要有:①由于有限元模拟软件的局限性,使得材料本构关系和实际情况存在一定差异;②套筒上轧制凹槽时,凹槽部位变薄,强度有所提高,这在有限元模型中没有反映出来;③灌浆料凝固时会有微膨胀的特性,相当于对钢筋和套筒施加了一个预压力,在模拟过程中没有体现。

由灌浆料拔出的荷载-位移曲线[图13(b)]可知,此类破坏模式的钢筋在弹性阶段的模拟结果与试验结果较吻合,两者弹性荷载分别为250、270 kN后进入屈服阶段,该阶段的模拟屈服承载力高于试验屈服承载力,分别为410、365 kN,随着位移继续增大,荷载-位移曲线开始出现下滑,最大位移均为4.2 mm,表明钢筋并未达到屈服,而连接件就已经停止了工作,但模拟结果与试验结果吻合较好,两者结果的荷载—位移曲线稍有偏差,这是由有限元软件的局限性导致的,但偏差在误差范围内,且结果仍然吻合得较好,表明采用ABAQUS建立的有限元模型正确。

通过以上分析,ABAQUS模拟软件计算数据与试验数据相差不大,同时表明套筒仍具有很大的安全储备空间,还有较大的优化空间。可以通过减小套筒壁厚尺寸达到节省材料、降低制作成本的效果。

对套筒壁厚进行数值模拟研究和优化分析。利用有限元分析软件ABAQUS建立5组关于新型灌浆套筒连接件的数值模型。采用单一变量的控制方法,对壁厚为5 mm、肋深分别为2、2.5、3、3.5、4 mm,其他材料性能和尺寸参数保持不变的情况下,对新型灌浆套筒不同凸肋深度进行研究。

3 新型灌浆套筒凸肋深度力学性能分析

模型采用的本构关系如图14所示,各材料采用的参数及力学性能指标如表2～表4所示。

表2 灌浆料的参数Table 2 Parameters of grouting material

表3 钢筋的参数Table 3 Parameters of reinforcement

表4 套筒的参数Table 4 Parameters of the sleeve

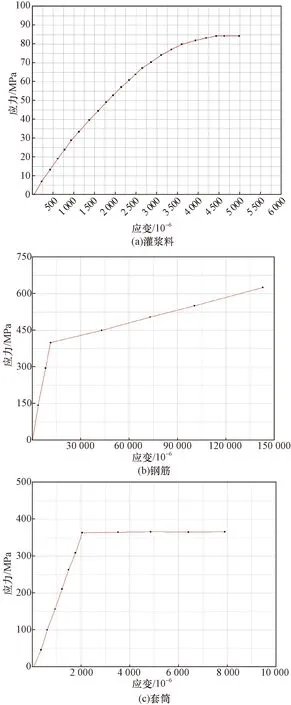
图14 材料本构模型Fig.14 Material constitutive model

3.1 本构及单元选择

新型灌浆套筒连接件的数值模型为三维实体模型,采用Conn3d2实体单元模拟三维情境下的实体结构,此单元也适合用来分析模型在轴向荷载作用下的复杂几何结构。

在新型钢筋灌浆套筒连接件的数值建模过程中,灌浆料采用ABAQUS损伤塑性模型(concrete damaged plasticity)[15],如图14(a)所示。

HRB400钢筋本构采用弹塑性加工硬化后的两折线模型[16],如图14(b)所示。

套筒材质类似钢筋,其本构采用弹性模型[17],如图14(c)所示。

参照新型灌浆套筒连接件计算模型各材料参数如表2～表4所示。

3.2 模型建立

采用壁厚为5 mm,肋间距为30 mm,凸肋深度为2、2.5、3、3.5、4 mm的无缝钢管。直径为32 mm的HRB400钢筋,厚度为12.5 mm的灌浆料组成的新型灌浆套筒,建立5组不同套筒凸肋深度的计算模型。新型灌浆套筒连接件相关尺寸及套筒凸肋深度参数如表5所示。

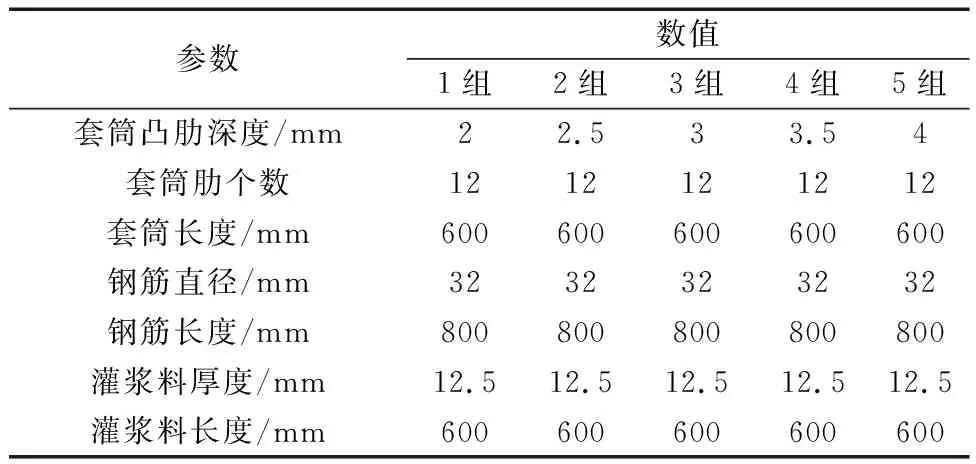
表5 新型灌浆套筒连接构件数值模型参数Table 5 Numerical model parameters of the new grouting sleeve connection member

模型采用的本构关系如图14所示。除套筒肋间距外,其余各材料采用的参数及力学性能指标如表2～表4所示。

3.3 模拟结果与分析

根据表5建立的新型灌浆套筒连接件数值模型,模拟计算得到的应力-应变曲线,如图15～图21所示。

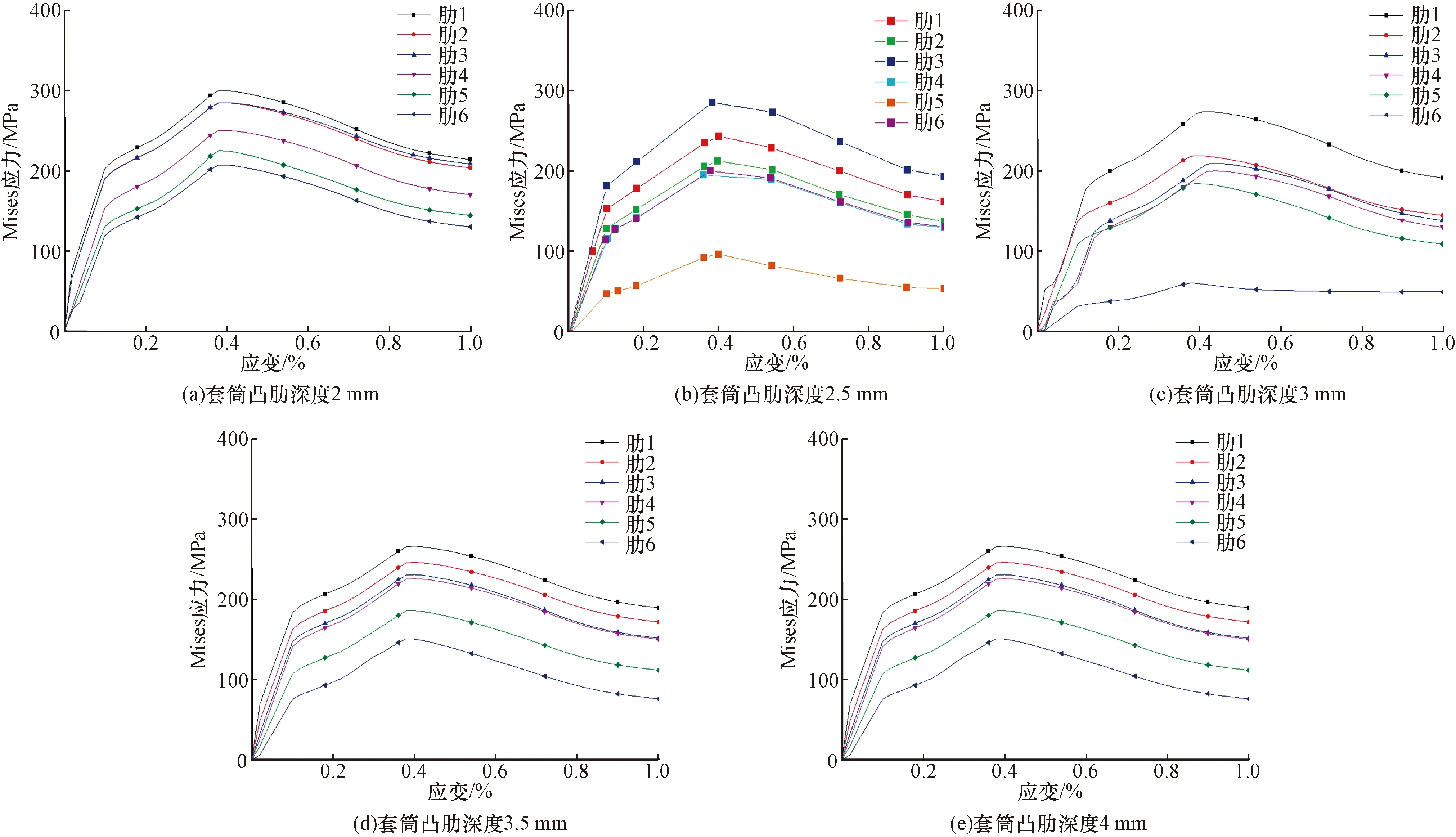
图15 套筒凸肋深度各肋Mises应力分布Fig.15 Mises stress distribution of each rib at convex rib depth

由图15套筒凸肋深度各肋Mises应力分布可知,套筒凸肋深度为2 mm时,肋1～肋6的Mises应力值分别为300、285、267、250、225、207 MPa;套筒凸肋深度为2.5 mm时,肋1～肋6的Mises应力值分别为245、216、291、204、98、203 MPa;套筒凸肋深度为3 mm时,肋1～肋6的Mises应力值分别为220、210、275、200、185、50 MPa;套筒凸肋深度为3.5 mm时,肋1～肋6的Mises应力值分别为265、245、230、225、185、150 MPa;套筒凸肋深度为4 mm时,肋1～肋6的Mises应力值分别为226、180、269、247、140、100 MPa;通过数据分析可知,套筒肋部受力较复杂,随着凸肋深度增加,肋1～肋4的Mises应力总体上较集中,肋5、肋6所受到的Mises应力反而较肋1～肋4的Mises应力有所降低,这是根据Sezen双段均布黏结应力模型[18]中钢筋弹性段和非弹性段长度决定的,即当肋布置在钢筋弹性长度范围内时,随着凸肋深度增加,肋部受到的Mises应力越大,当肋布置在钢筋非弹性长度范围内时,随着肋深度增加,肋部受到的Mises应力越小。

由图16套筒极限应力与凸肋深度关系可知,随着套筒凸肋深度增加,套筒所能承受的极限应力逐渐增大,当凸肋深度达到一定程度时,其极限应力下降明显,当套筒凸肋深度为2、2.5、3 mm时,套筒所能承受的极限应力呈线性增长,极限应力值分别为303、310、318 MPa;当凸肋深度为3.5、4 mm时,套筒所能承受的极限应力急剧下降,极限应力值分别为307、305 MPa。由极限应力分析表明,以上套筒均能满足工程安全所需,当凸肋深度为3 mm时,套筒所受极限应力最大,当凸肋深度为4 mm时,套筒所受极限应力最小,可见凸肋深度为3 mm时套筒受力最优。

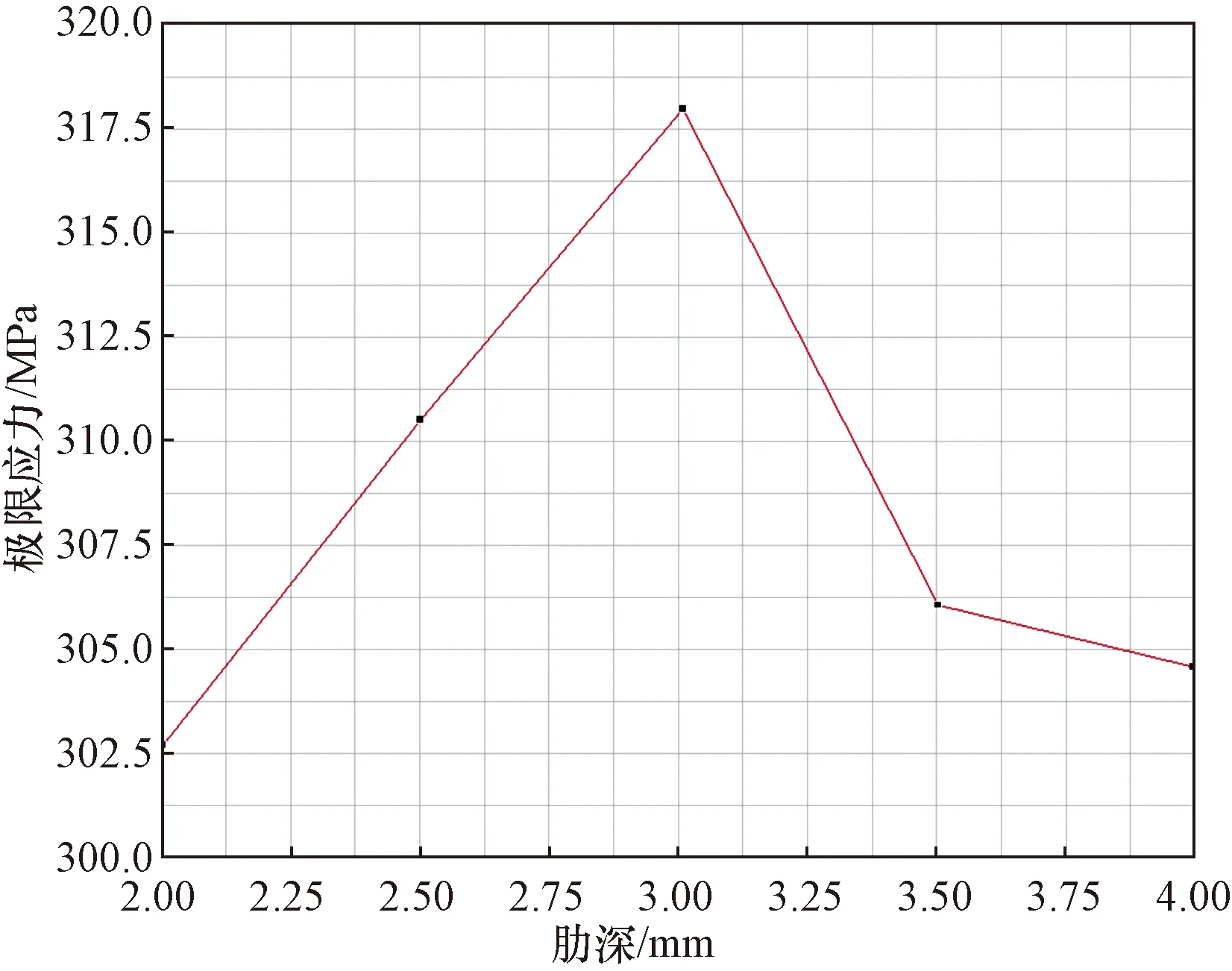
图16 套筒极限应力与凸肋深度关系Fig.16 Relationship between ultimate stress of sleeve and depth of convex rib

由图17套筒轴向应力与凸肋深度关系可得,当套筒凸肋深度为2、2.5、3、3.5、4 mm时,其轴向应力分别为301.5、296.5、309.1、302.5、294.3 MPa,可见,除凸肋深2 mm以外,套筒轴向应力变化趋势与图16一致,随着套筒凸肋深度增加,套筒所能承受的轴向应力逐渐增大,当凸肋深度超过3 mm时,其轴向应力下降明显,套筒所能承受的轴向应力越来越低。

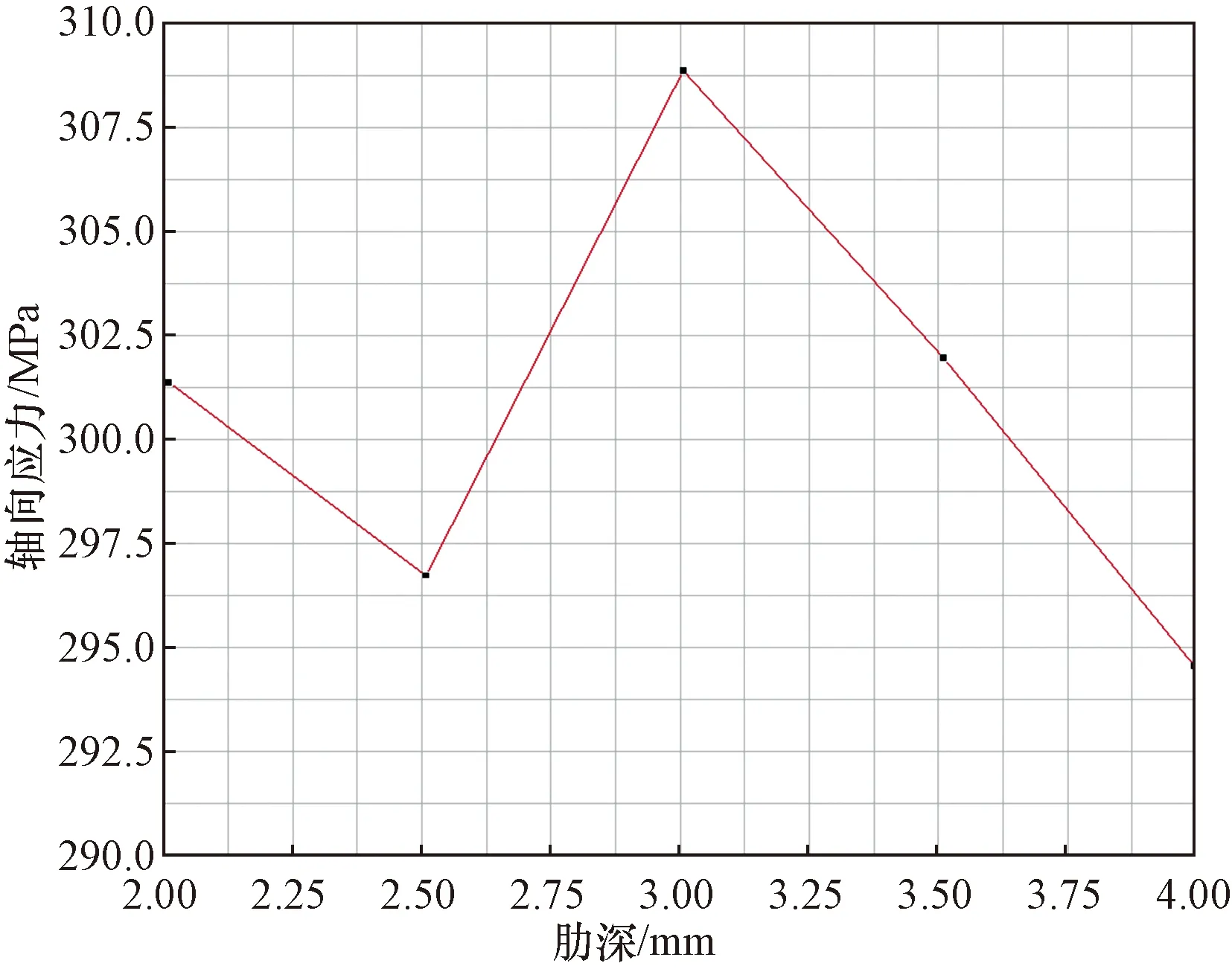
图17 套筒轴向应力与凸肋深度关系Fig.17 Relationship between axial stress of sleeve and rib depth

由图18套筒切向应力与套筒凸肋深度关系可得,当套筒凸肋深度在2～2.5 mm时,套筒切向应力越来越低;当套筒凸肋深度在2.5～3.5 mm时,套筒切向应力呈线性增长;套筒凸肋深度超过3.5 mm后,套筒切向应力又开始越来越低。当套筒凸肋深度为2.5 mm时,切向应力值最小,为5 MPa;当套筒凸肋深度为3.5 mm时,切向应力值最大,为17 MPa,纵观其各切向应力取平均值后发现,当套筒凸肋深度为3 mm时,其切向应力值较接近平均值。

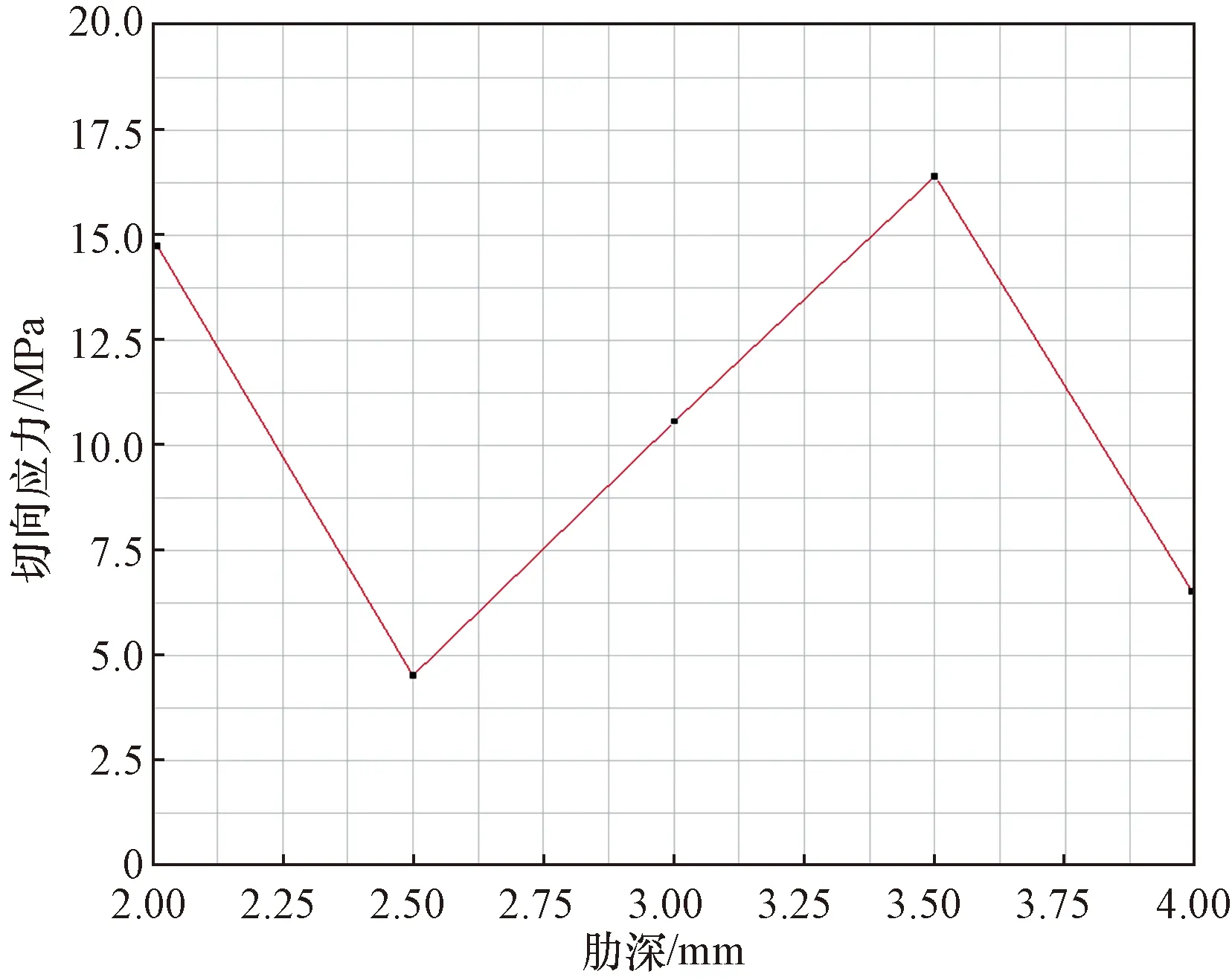
图18 套筒切向应力与凸肋深度关系Fig.18 Relationship between tangential stress of sleeve and convex rib depth

由图19套筒位移与套筒凸肋深度关系可知,随着套筒凸肋深度增加,其位移变化较缓,总体上相差不大,当凸肋深度为4 mm时,套筒的位移值最小,为5.62 mm,当凸肋深度为2、2.5、3、3.5 mm时,套筒位移值分别为5.71、5.75、5.74、5.76 mm,由上述数据分析可知,当套筒凸肋深度为3 mm时,其位移值最接近整体平均值,为5.75 mm,表明凸肋深度为3 mm的套筒产生的位移变形较其他凸肋深度的套筒稳定。

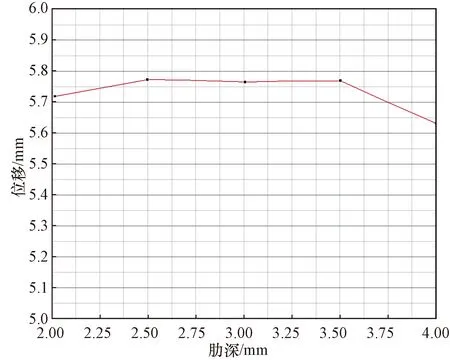
图19 套筒位移与凸肋深度关系Fig.19 Relationship between sleeve displacement and convex rib depth

图20所示的套筒凸肋深度与灌浆料第三主应力关系图中的值是原始值增大10倍后的结果,由图20、图21可知,当套筒凸肋深度为2 mm时,灌浆料第三主应力值最大,最大值为10.9 MPa;当套筒凸肋深度为2.5、3、3.5 mm时,随着套筒凸肋深度增加,灌浆料第三主应力值逐渐趋于一个稳定值,分别为6、5.9、6.1 MPa;当凸肋深度达到4 mm时,此时灌浆料第三主应力有所下降,即比凸肋深度为2 mm时的第三主应力要低,为7.1 MPa。分析可知,套筒在一定凸肋深度范围内,增加其内部凸肋深度有利于提高套筒连接件整体受力性能,当凸肋深度超过一定范围后,构件承载力有所下降。

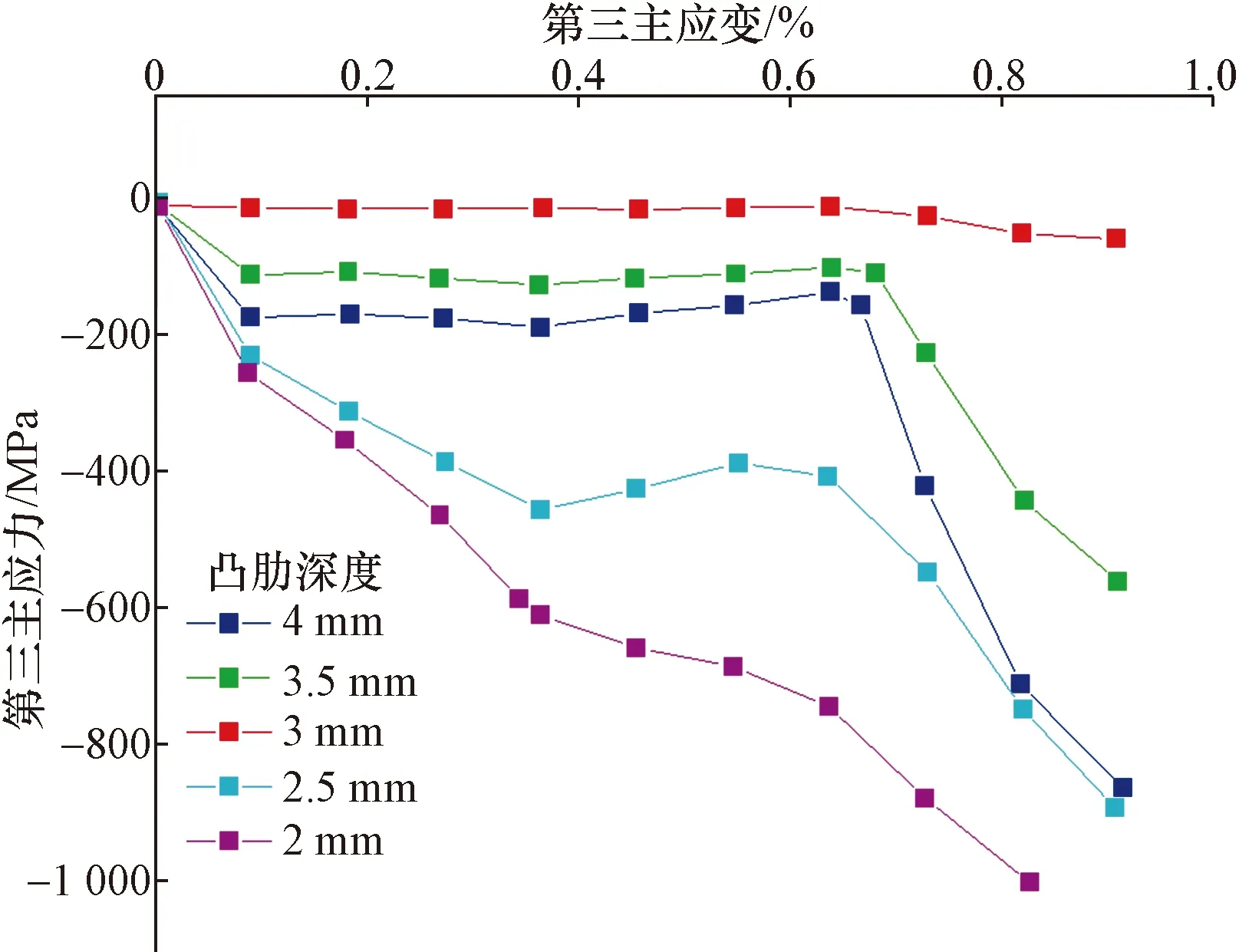
图20 灌浆料凸肋深度第三主应力与第三主应变关系Fig.20 Relationship between the third principal stress and the third principal strain at the depth of grout rib

图21 套筒内部凸肋深度与灌浆料第三主应力关系Fig.21 Relationship between depth of convex rib inside sleeve and third principal stress of grouting material

综上所述,当套筒凸肋深度为3 mm时,其受力最优,可见能满足工程需要的同时还能节约制作成本。

4 结论

在试验的基础上,采用ABAQUS有限元分析软件,进行单向拉伸试验、新型灌浆套筒凸肋深度力学性能分析。得出以下结论。

(1)通过以上分析,ABAQUS模拟软件计算数据与试验数据相差不大,表明软件计算结果具备可靠性。

(2)由套筒凸肋深度各肋Mises应力分布可知,当肋布置在钢筋弹性长度范围内时,随着凸肋深度增加,肋部受到的Mises应力越大,当肋布置在钢筋非弹性长度范围内时,随着肋深度增加,肋部受到的Mises应力越小。

(3)由套筒极限应力与凸肋深度关系可知,随着套筒凸肋深度增加,套筒所能承受的极限应力逐渐增大;由套筒位移与套筒凸肋深度关系可知,随着套筒凸肋深度增加,其位移变化较缓,总体上相差不大。

(4)由套筒轴向应力与凸肋深度关系可得,随着套筒凸肋深度增加,套筒所能承受的轴向应力逐渐增大,当凸肋深度超过3 mm时,其轴向应力下降明显,套筒所能承受的轴向应力越来越低。

(5)由套筒凸肋深度与灌浆料第三主应力关系可知,套筒在一定凸肋深度范围内,增加其内部凸肋深度有利于提高套筒连接件整体受力性能,当凸肋深度超过一定范围后,构件承载力有所下降。

综上所述,当套筒凸肋深度为3 mm时,其受力最优,即能满足工程需要的同时还能节约制作成本。