商业健康保险对中国经济增长和波动的影响研究

邵全权，刘 宇，杨 浩，张嘉文

（南开大学 金融学院，天津 300350）

一、引言

健康保险可划分为政府筹办的公共健康保险和商业保险公司筹办的商业健康保险。我国的基本医疗保险目前已经基本实现全面覆盖，但是基本医疗保险只能起到基础性保障作用，不能满足人们多层次的医疗保障需求。商业健康保险作为基本医疗保险的有效补充，能够满足不同人群的健康需求，缓解基本医疗保险基金不足的压力，对完善多层次的医疗保障体系具有重要作用，然而目前商业健康保险尚未发挥其全部作用。

当前我国经济下行压力不断增大，同时面临人口老龄化程度不断加深、医保基金支付能力不足、中美贸易摩擦等问题，诸多社会、经济问题相互交织，对我国经济增长产生了巨大影响，成为许多学者研究关注的重点。

健康保险作为一种金融工具，能够在一定程度上缓解以上社会、经济问题带来的经济增长压力，许多学者研究过健康保险和消费者个体、经济增长之间的关系。从消费者角度来看，健康保险主要影响劳动供给和消费决策，健康保险通过改善个体的健康状况，增加劳动时长。同时，健康风险带来的不确定性被固定为确定的保费支出，降低了消费者面临的不确定性，进而会影响个体的消费决策。而当个体普遍改变劳动行为和消费行为时，经济增长也会受到影响。所以，从经济增长角度看，健康保险可以增加个体劳动，缓解人口老龄化带来的负面影响和劳动力供给不足的问题。此外，医疗服务等产业也伴随健康保险的普及得到发展，从而刺激投资，拉动经济增长。在现代社会，人们面临的风险和不确定性因素不断增加，受到健康冲击的可能性也在增大，人们对健康保障的需求不断增加。国家对此也十分重视，2020 年2 月发布的《中共中央国务院关于深化医疗保障制度改革的意见》，提出要坚持以人民健康为中心，加快建成多层次医疗保障体系，加快发展商业健康保险。因此，商业健康保险未来有着很大的发展空间，也必将对经济增长产生更深远的影响。然而，以往的文献大多从社会医疗保险的角度出发研究健康保险对经济增长的影响，很少从商业健康保险的角度进行研究。除此之外，也很少有研究关注健康保险在经济稳定方面所发挥的作用。在上述背景下，研究商业健康保险对经济增长和经济波动的影响具有重要的理论和现实意义。

本文基于以上分析，结合理论和实证两个方面研究了商业健康保险与经济增长、经济波动之间的关系。在理论方面，本文引入人力健康资本，建立了相关理论模型，说明了在不同情况下商业健康保险对经济增长的影响。在实证研究方面，本文以我国31 个省份作为研究样本，研究了各地区商业健康保险对经济增长的影响。最后，本文结合理论和实证的研究结果对我国商业健康保险的发展提出一些建议，希望商业健康保险的发展能够更好地满足人民群众的需要，促进经济更健康发展。

二、文献综述

关于健康保险与经济增长之间的关系，国内外相关文献较为丰富，以往的研究主要从就业与劳动供给、医疗费用支出及相关影响因素、消费者行为和决策三个角度来进行分析，也得到了不同的结论。首先，健康保险能够改善参保劳动者的健康状况和就业选择。拥有健康保险可以降低人们因为健康状况恶化而导致失业和负债的风险，进而影响到劳动力市场供给情况，从而对整个国民经济产生重要影响。MALLOY 等［1］以美国48 个州和经合组织国家作为研究对象，发现扩大劳动年龄人口的医疗保险覆盖面，能够增加就业和促进经济增长。STERRET 等［2］则发现医疗保险能够消除工作锁定，并在一定程度上减少就业过程中对残疾人、老年人等群体的不平等现象，进而增加社会劳动力供给并促进经济增长。其次，健康保险的推行，会直接影响到社会医疗费用支出情况以及相关健康服务产业发展，从而影响经济增长。CHEN 等［3］发现包括医疗保险在内的社会保障可以显著提高居民的消费水平，有效地拉动内需，创造部门收入与工作机会，从而刺激经济发展。不过，也有研究表明政府采取的一些健康保险相关政策会对经济增长产生不利影响。公共医疗保险是建立在政府财政支持的基础上的，公共医疗保险支出的增加，可能会导致教育、基础设施等其他领域的经费支出减少。KUNZE［4］利用利他主义OLG 模型研究，发现不同的收付制度会带来不同影响，其中现收现付制不利于经济增长。IHORI 等［5］通过研究日本的医疗保险改革发现，医疗保险共同支付率上升所增加的道德风险会抑制经济增长，而将公共医疗保险支出固定在GDP 一定比例的政策也会抑制经济增长。除此之外，朱铭来和胡祈［6］则发现公共医疗保险能够抑制医疗卫生支出对经济产生的短期不利影响，而商业健康保险能够抑制其对长期经济增长的不利影响。最后，健康保险能够改变参保者的收入和福利状况，从而影响参保者消费和储蓄决策，进而影响经济增长。健康保险能够减少家庭储蓄［7-8］，从而促进消费。进一步地，ZHAO［9］研究发现健康保险对家庭的食品支出、非食品支出均有显著促进作用，但在不同收入水平的家庭存在较大异质性。除此之外，也有学者进行了其他方面的理论和实证研究。ZHENG［10］通过对中国社会医疗保险改革的研究，发现提高个人账户的贡献率有利于物质资本和人力资本积累，能够促进经济增长；郑莉莉［11］通过基于VAR 模型的实证研究，发现社会医疗保险与经济增长之间存在长期协整关系，医保覆盖率的提高从长期来看有助于促进经济增长；而周小菲等［12］则认为社会医疗保险能够促进短期经济增长，对长期经济增长的影响不显著。

综上所述，国内外现有文献主要从公共医疗保险的角度来研究健康保险与经济增长之间的关系，涉及商业健康保险的研究较少，同时也很少有文献关注健康保险对经济波动的影响。因此，本文在研究对象方面，选择商业健康保险来探究其与经济增长、经济波动之间的关系。在研究方法方面，本文通过引入健康人力资本构建了商业健康保险与经济增长、经济波动之间关系的理论模型，同时结合数值模拟探讨了在改变影响保费的相应因素的情况下，健康保险对经济增长和波动有何种影响。在实证研究方面，选择中国31 个省份作为研究样本，分析商业健康保险对中国经济增长和经济波动的影响。

三、模型设定与数值模拟

（一）模型设定

1.家庭

借鉴邵全权等［13］关于风险冲击、保险保障与宏观经济波动的研究，设定本文包含健康风险冲击和商业健康保险保障的数理模型。借鉴邵全权等［13］关于效用函数的设定，在效用函数中引入健康人力资本。考虑家庭“长生不老”的情况，家庭通过消费和健康人力资本产生CRRA 形式的正效用。不同于邵全权等［13］的研究将健康人力资本设定为总资本的函数，本文采用更加微观的代表性家庭的假设，将健康人力资本设定为家庭资产的函数。因此家庭的效用函数如下式所列：

其中β表示贴现率，Ct表示t 期的消费，at为t期的家庭资产，γ1是消费的相对风险厌恶系数，γ2是健康的相对风险厌恶系数，θ用来表示健康的相对重要程度。假设健康人力资本是完全折旧的，设定当期的健康水平h=(τat)η，η为健康弹性。在动态规划问题式（1）的每个阶段，家庭资产中的一部分用于卫生支出，该比例为τ。

2.资产的动态

本文假设代表性家庭的资产演进规律由收入减去支出刻画。收入来自家庭的劳务收益和通过持有资产产生的收益，支出由消费和商业健康保险保费构成。家庭的劳务收益为资产的线性函数eat，e为劳务收益占资产的比重。家庭的劳务收益面临健康风险的冲击，出现概率为p，如果发生健康风险，会对劳务收益造成程度为d 的降低，在购买商业健康保险的情形下可以获得健康保险扣除免赔率为比例m后的保险金赔付（相应的健康保险保障程度为1-m），健康保险免赔比例为m。根据邵全权等［13］研究，可以由此设定健康保险的保险乘子：b=1-pdm。本文建立模型为离散模型，资产收益率R 为毛收益率。健康保险保费为μpd(1-m)eat，其中pd(1-m)eat为精算公平保费，μ为反映健康保险行业市场力量和健康保险公司对利润要求的系数。基于上述设定，家庭资产的演化规律由式（2）确定：

3.动态规划算法

基于前述有关设定，本文动态规划问题的贝尔曼方程可以写为：

设定初始资产at∈[0.1,5]，t+1 期家庭终生效用贴现值V(at+1)初始值为0，基于此和式（3）计算t期家庭终生效用贴现值V(at)，将V(at+1)赋值为V(at)，迭代贝尔曼方程直到收敛，然后再根据式（2）确定at的时间路径。根据BARRO等［14］，均衡时人均资本等于人均资产，即at=kt［13］。生产函数具有劳动增进型技术进步的特点：人均有效产出形式为：，α为生产函数的资本份额。人均有效资本和人均有效产出分别为kt和yt，通过at实现kt和yt的增长序列。再通过设定的人口增长率n 和技术进步率x，得到总资本和总产出Kt和Yt的增长序列。对基于上述方式实现的时间序列，运用HP 滤波的方式计算得到经济波动的时间序列。最后对影响健康保险保费的关键参数p、d、m、μ设置不同取值，以此得到上述参数改变对经济增长和经济波动的影响规律，再综合上述规律探讨健康保险保费变化对经济增长和经济波动的影响。

（二）参数校准

本部分进行参数校准。根据陈国进等［15］、邵全权等［13］的研究成果，本文把资本份额α校准为0.3，将折现因子β的取值设为0.95。借鉴骆永民［16］的成果，本文将健康的效用值参数θ设定为0.45，卫生支出对健康水平的弹性η校准为0.1。关于τ的校准主要参考庄子罐［17］的观点，根据历年《中国卫生和计划生育统计年鉴》计算历年卫生总费用占GDP 的比重的平均值，将τ校准为0.012 46。借鉴陈国进等［15］、邵全权等［13］的研究，分别将消费与健康的相对风险规避系数γ1设定为0.85，γ2设定为0.9。依据中国家庭金融调查，中国居民家庭年资产增值率大致为12%，因此将资产收益率R 设定为1.12。根据《中华人民共和国2015年国民经济和社会发展统计公报》和《中国家庭发展报告2015》，选取全国居民人均可支配收入并计算家庭人均初始资产，最终将e设定为0.071 8。结合中国近年来人口自然增长率大约为3‰～5‰的现实情况，将人口增长率n设定为5‰。参考王小鲁［18］、徐淑丹［19］、杨旭等［20］的研究，将技术进步率Z校准为0.02（见表1）。

根据前文所述，健康保险保费为μpd(1-m)eat，影响保费的关键参数为出险概率p、损失程度d、免赔比例m，以及市场力量参数μ，在接下来的数值模拟中，将对上述4 个参数进行不同的赋值模拟，以此观察参数改变对经济增长和经济波动的影响，并最终将其运用于健康保险保费对经济增长和经济波动的影响方面。具体而言，p 分别取值为0.1、0.2、0.3，d 分别取值为0.1、0.3、0.5，m 分别取值为0.1、0.3、0.5，μ分别取值为1、1.5、2。

（三）数值模拟

基于前述理论模型与参数校准，本部分进行相应的数值模拟。在运用贝尔曼方程进行值函数迭代的基础上，得到在每一个初始资本点上的下一期的人均资本和当期消费，然后选取第200 个初始资本点进行经济增长时间序列的模拟，并基于此对增长序列赋以HP滤波得到经济波动的时间序列。本文还尝试选取其他不同的初始资本点进行时间序列的模拟，结果并未改变基本结论。重复上述过程，并对商业健康保险有关参数予以不同的赋值，进而可以得到出险概率p、损失程度d、免赔比例m以及市场力量参数μ的变化对经济增长和经济波动的影响规律。

1.健康保险对经济增长的影响

我们首先关注出险概率p、损失程度d、免赔比例m 以及市场力量参数μ的变化对经济增长的影响。图1—图4 分别显示p、d、m、μ取不同数值时经济增长趋势曲线的演化规律。在出险概率p 的影响方面，无论是在人均有效资本与人均有效产出的增长方面，还是在总资本和总产出的增长方面，在p=0.1 时经济增长最高，在p=0.3 时经济增长次之，在p=0.2 时经济增长最低。这表明p 对经济增长的影响存在非单调的影响效应，当p 从较低水平向较高水平变化时，存在一个临界点（对应图1 中为0.2），小于该点时p的提高会抑制经济增长，大于该点时p 的提高会促进经济增长，p 较高时对经济增长促进的程度要低于p 较低时对经济增长抑制的程度。因此，p 较低时会抑制经济增长，p 较高时会促进经济增长。

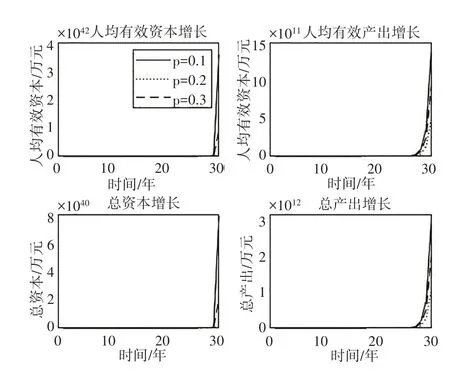
图1 p变化对经济增长的影响

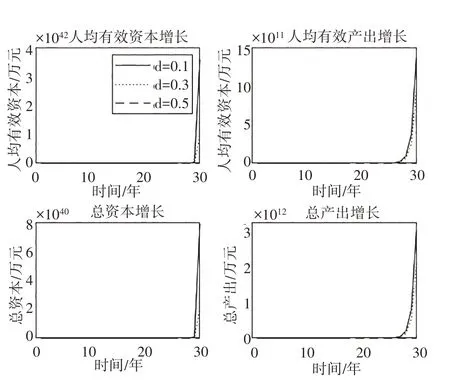
图2 d变化对经济增长的影响

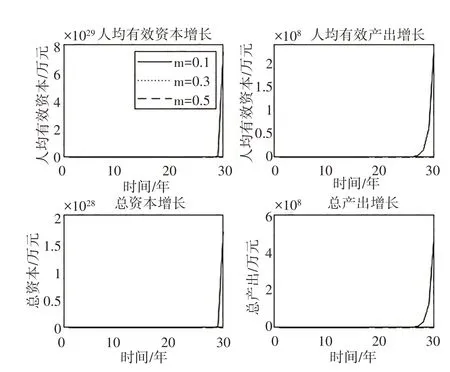
图3 m变化对经济增长的影响

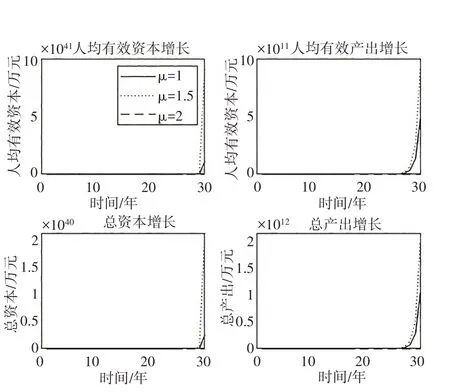
图4 μ变化对经济增长的影响

在损失程度d 的影响方面，无论是人均有效资本与人均有效产出的增长，还是总资本和总产出的增长都体现出一致的规律，d 的不同取值对经济增长的影响表明，随着d 提高，经济增长逐渐放缓，说明d的提高会抑制经济增长。

在免赔比例m的影响方面，无论是人均有效资本与人均有效产出的增长，还是总资本和总产出的增长都体现出一致的规律，m 的不同取值对经济增长的影响表明，随着m 提高，经济增长速度逐渐降低，说明m的提高会抑制经济增长。正如前文中指出，免赔比例m 通过（1-m）反映保险保障程度，上述结论表明，提高健康保险保障程度会促进经济增长。

在市场力量参数μ的影响方面，无论是人均有效资本与人均有效产出的增长，还是总资本和总产出的增长，在μ=1.5 时经济增速最高，在μ=1 时经济增速次之，在μ=2 时经济增速最低。这表明μ对经济增长存在非单调的影响效应，当μ从较低水平向较高水平变化时，存在一个临界点（对应图4 中为1.5），小于该点时μ的提高会促进经济增长，大于该点时μ的提高会抑制经济增长，μ较低时对经济增长促进的作用要小于μ较高时对经济增长抑制的作用。因此，μ较低时会促进经济增长，μ较高时会抑制经济增长。

2.健康保险对经济波动的影响

然后我们关注出险概率p、损失程度d、免赔比例m 以及市场力量参数μ的变化对经济波动的影响。图5—图8 分别显示p、d、m、μ取不同数值时经济波动趋势曲线的演化规律。在出险概率p的影响方面，无论是人均有效资本与人均有效产出的波动，还是总资本和总产出的波动，在p=0.1时经济波动幅度最大，在p=0.3 时经济波动幅度次之，在p=0.2 时经济波动幅度最小。这表明p 对经济波动的影响存在非单调的影响效应，当p 从较低水平向较高水平变化时，存在一个临界点（对应图5 中为0.2），小于该点时p 的提高会减小经济波动幅度，大于该点时p的提高会加大经济波动幅度，p较高时对经济波动加大的幅度要低于p 较低时对经济波动减小的幅度。因此，p 较低时会减小经济波动幅度，p较高时会加大经济波动幅度。

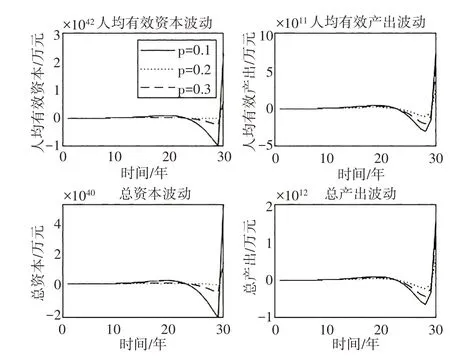
图5 p变化对经济波动的影响

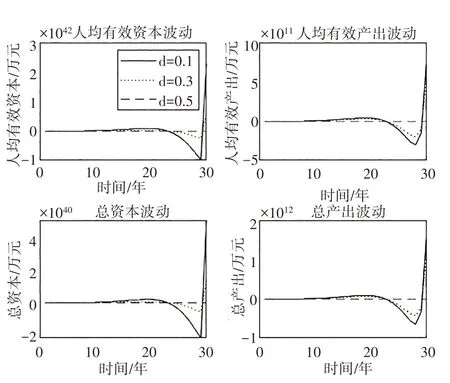
图6 d变化对经济波动的影响

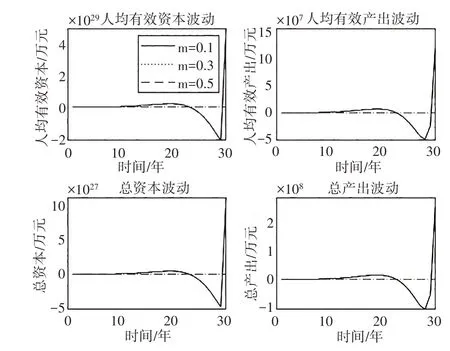
图7 m变化对经济波动的影响

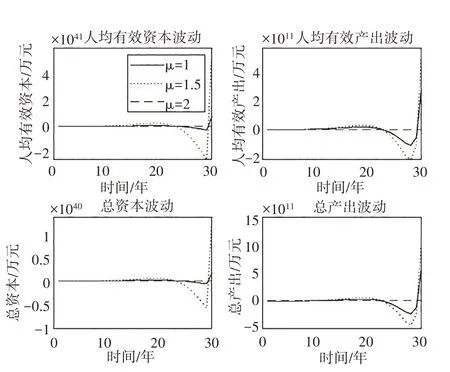
图8 μ变化对经济波动的影响

在损失程度d 的影响方面，无论是人均有效资本与人均有效产出的波动，还是总资本和总产出的波动都体现出一致的规律，d 的不同取值对经济波动的影响表明，随着d 提高，经济波动幅度逐渐减小，说明d的提高会减小经济波动幅度。

在免赔比例m的影响方面，无论是人均有效资本与人均有效产出的波动，还是总资本和总产出的波动都体现出一致的规律，m 的不同取值对经济波动的影响表明，随着m 提高，经济波动幅度逐渐减小，说明m的提高会减小经济波动幅度。正如前文中指出，免赔比例m 通过（1-m）反映保险保障程度，上述结论表明，提高健康保险保障程度会加大经济波动幅度。

在市场力量参数μ的影响方面，无论是人均有效资本与人均有效产出的波动，还是总资本和总产出的波动，在μ=1.5 时经济波动幅度最大，在μ=1 时经济波动幅度次之，在μ=2 时经济波动幅度最小。这表明μ对经济波动的影响存在非单调的影响效应，当μ从较低水平向较高水平变化时，存在一个临界点（对应图8中为1.5），小于该点时μ的提高会加大经济波动，大于该点时μ的提高会减小经济波动，μ较低时对经济波动加大的幅度要低于μ较高时对经济波动减小的幅度。因此，μ较低时会加大经济波动幅度，μ较高时会减小经济波动幅度。

综上所述，在健康保险有关参数对经济增长的影响方面，p 较低时会抑制经济增长，p 较高时会促进经济增长；d的提高会抑制经济增长；m的提高会抑制经济增长，健康保险保障程度的提高会促进经济增长；μ较低时会促进经济增长，μ较高时会抑制经济增长。在健康保险有关参数对经济波动的影响方面，p 较低时会减小经济波动幅度，p 较高时会加大经济波动幅度；d 的提高会减小经济波动幅度；m 的提高会减小经济波动幅度，健康保险保障程度的提高会加大经济波动幅度；μ较低时会加大经济波动幅度，μ较高时会减小经济波动幅度。

结合前文中关于健康保险保费的公式，可以发现，如果健康保险保费的提高是由于损失程度d 的提高，那么会抑制经济增长并减小经济波动幅度；如果健康保险保费的提高是由于免赔额度m 的降低（对应1-m 提高，保障程度提高），那么会促进经济增长并加大经济波动幅度；如果健康保险保费的提高是由于出险概率p 的提高，则要考虑p 的初始状态，初始p 较低时会抑制经济增长并减小经济波动幅度，初始p 较高时会促进经济增长并加大经济波动幅度；如果健康保险保费的提高是由于市场力量参数μ的提高，则要考虑μ的初始状态，初始μ较低时会促进经济增长并加大经济波动幅度，初始μ较高时会抑制经济增长并减小经济波动幅度。由于健康保险保费主要由上述参数p、d、m、μ确定，因此，保费提高对经济增长和经济波动的影响也需要结合上述规律加以综合考量，无法直接得出提高保费对经济增长和经济波动有影响的简单结论，需要深入分析保费提高的结构性因素，即保费的提高是如何受到参数p、d、m、μ变化所致。基于此才能分析提高保费对经济增长和经济波动产生的最终效应。

四、计量模型设定与变量说明

（一）模型设定

1.面板门槛模型

商业健康保险与经济增长之间的关系可能与地区经济发展水平以及保险业发展水平有关，本文的计量模型选择采用面板门槛模型，通过对样本进行分组回归，考察不同组别内商业健康保险对经济增长和经济波动有何不同影响。借鉴HANSEN［21］的研究成果，设定单一门槛模型的计量方程。

在模型（4）中，i 代表省份，t 代表年份；λi代表不可观测的地区效应，用来控制省份的固定效应；xit为受门槛变量影响的解释变量，qit为门槛变量，γ为待确定的门槛值，β1和β2分别为门槛变量在不同区制时解释变量xit对被解释变量yit的影响系数；1(·)是一个示性函数，满足括号内条件时取值为1，否则取值为0；εit为误差项，服从独立同分布。类似地，可以推广到包含多个门槛值的门槛回归。

yit代表被解释变量，包括GDP 的对数和经济增长率；xit代表解释变量，包括商业健康保险保费的对数、商业健康保险的保险深度、商业健康保险的保险密度的对数等三个变量；X是其他控制变量的集合。

2.动态面板门槛模型

HANSEN［21］的面板门槛模型是静态的，模型中固定效应估计量要求协变量是强外生的，然而强外生性在实际应用中可能会受到限制。SEO 和SHIN［22］在该模型基础上扩展了具有潜在内生阈值变量的动态面板门槛模型，提出了一阶差分GMM估计的方法，使该模型允许存在滞后因变量与内生协变量。考虑动态面板的门槛模型如下：

其中，xit为n×1 阶变量，可包括滞后因变量，qit为门槛变量，当样本n增长到无穷大时，我们假设T是一个固定值。1{}是一个示性函数，模型中εit被假定为一个鞅差序列，允许了回归变量与阈值变量的内生性。估计过程包括以下4个步骤。

第一步，首先通过一阶差分变换去除附带参数μi，得到：

然后，引入加权矩阵Wn的GMM准则函数：

在给定γ的前提下，θ的GMM 估计量是使式（7）达到最小化时θ的值。求解得：

第三步，将式（8）代入式（7）得到，进而得到

第四步，借鉴SEO 和SHIN［22］的方法，构建本文单一的动态面板门槛模型：

其中，i代表省份，t代表年份；yi,t-1为因变量经济增长或者经济波动的滞后项；xit为受门槛变量影响的商业健康保险的三种内生解释变量；qit为门槛变量也就是相对保险深度；γ为待确定的门槛值；1(·)是一个示性函数，满足括号内条件取值为1，否则取值为0；εit为误差项，服从独立同分布。变量含义与前面的面板门槛模型一致。

（二）变量选取与说明

1.被解释变量、解释变量与控制变量

对被解释变量的选择，本文从经济增长和经济波动两个方面来衡量。前者通常采用人均GDP 的对数来衡量，这是因为人均GDP 在反映GDP 的增长情况的同时，还能够反映人口与经济增长的关系。本文借鉴邵全权［23］的研究，采用经济增长率来衡量后者，用来反映经济增长水平的变化程度，体现经济波动的情况。

在解释变量方面，本文采用商业健康保险保费的对数、商业健康保险的保险深度、商业健康保险的保险密度的对数等三个指标来综合反映一个地区商业健康保险的发展情况。这三个变量也是以往文献大多采用的指标，其中商业健康保险保费的对数从保费数量方面直观地反映了商业健康保险的发展情况，属于绝对指标；同时，本文加入商业健康保险的保险密度的对数和商业健康保险的保险深度指标作为相对指标，前者用来反映商业健康保险的行业发展规模，后者则用来反映商业健康保险在地区经济的地位。

在控制变量方面，经济增长的影响因素很多，本文从投资、教育、健康、社会保障以及政府财政等角度来选择控制变量。本文用全社会固定资产投资总额的对数来衡量物质资本，代表投资对经济的拉动作用；采用每十万人中高校学生人数的对数来衡量教育水平；在健康水平方面，一般采用死亡率和预期寿命来衡量。由于我国预期寿命的统计数据不连续，因此本文采用了死亡率。另外借鉴王文静等［24］对健康人力资本指标的选取，本文加入每千人卫生技术人员数和每千人拥有病床数两个指标来衡量健康水平。教育和健康两个方面的变量主要用来衡量人力资本对经济增长的影响，两者分别代表了教育人力资本和健康人力资本，综合反映了劳动力的素质。良好的就业和社会保障会促进社会消费，也是影响经济增长的重要因素，本文将就业和社会保障支出的对数作为控制变量。同时，地方财政支出水平在一定程度上反映了地方政府对经济的影响程度，本文将地方一般财政支出的对数作为控制变量。

2.工具变量

商业健康保险与经济增长二者之间可能产生相互影响的情况，为了避免模型可能导致的内生性问题，本文选用工具变量法进行实证分析。在研究保险与经济增长的关系方面，郑伟和刘永东［25］提出了“保险基准深度比”这一概念，将保险深度与地区经济发展阶段联系了起来，用来反映一个地区保险业的相对增长水平。邵全权［23］在此基础上，提出了相对保险深度这一概念，通过构建保险业增长模型，进行代入估计，计算出一个地区理论上应该达到的基准保险深度，再将地区实际的保险深度除以基准保险深度得到相对保险深度，用来衡量保险业发展水平。本文采用各省份商业健康保险的相对保险深度作为工具变量。从相关性方面来看，商业健康保险的相对保险深度衡量的是一个地区商业健康保险行业的发展水平，与商业健康保险的保费、保险深度、保险密度等指标之间必然存在相关关系。从外生性方面来看，商业健康保险的相对保险深度只是代表商业健康保险与理论发展预期的一个比较，同时也是一个相对数，与地区经济之间并无必然联系；反过来，经济增长也不会影响到相对保险深度。因此，选择相对保险深度作为工具变量，满足工具变量的要求。

3.门槛变量

本文采用商业健康保险的相对保险深度作为门槛变量。相对保险深度衡量的是保险业的发展水平，商业健康保险的相对保险深度实际上就是根据各地区商业健康保险的实际保险深度超过基准保险深度的程度，把各地区商业健康保险发展情况划分成了不同的阶段。

（三）数据来源与描述性统计

本文选取的样本数据为2010—2021 年我国31 个省份宏观层面的面板数据，数据主要来源于EPS 数据平台。其中，由于大连、宁波、青岛、厦门和深圳等5 个城市的保费数据单独统计，因此这些城市的保费并未被纳入各省份健康保险保费收入。商业健康保险的保险密度、保险深度以及相对保险深度通过整理计算而来。参考邵全权［23］的方法计算商业健康保险的相对保险深度，相对保险深度=。用商业健康保险的保险深度与人均GDP 的对数进行非线性最小二乘回归，估计系数为b1-b3，然后代入模型得到基准保险深度；再用各省份历年实际保险深度除以基准保险深度，从而得到商业健康保险的相对保险深度。本文主要研究变量的描述性统计结果如表2所示。

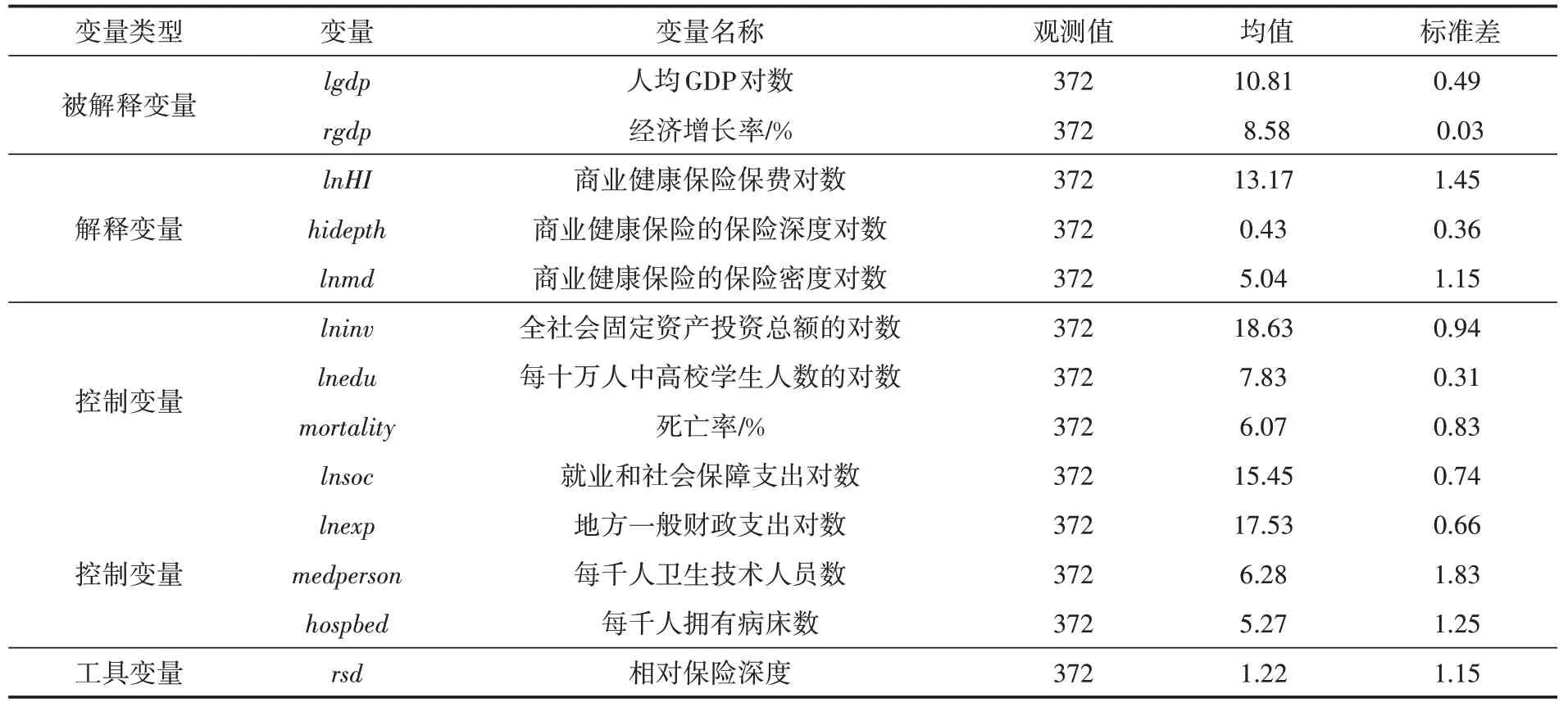
表2 变量描述性统计

五、实证结果分析

（一）基准回归结果

1.商业健康保险对经济增长的影响

表3 的门槛效应检验结果表明，商业健康保险保费的对数和保险密度的对数与人均GDP 的对数之间存在显著的双重门槛效应。以商业健康保险的相对保险深度作为门槛变量，实际上是根据各地区商业健康保险的实际保险深度超过基准保险深度的程度，把各地区商业健康保险发展情况划分成了低、中和高三个不同的阶段。在表3 中，商业健康保险的保费、保险密度与经济增长之间存在显著的正相关关系，但是随着商业健康保险保费规模的不断增加，商业健康保险对经济增长的促进作用也在不断减弱，这是由于随着商业健康保险市场走向成熟，单纯由保费规模增加所带来的经济和社会效益在不断降低。另外，商业健康保险的保险深度同样存在明显的门槛效应，从其对经济增长的影响系数可以看到，其在相对保险深度处于2.597 9 前后发生了较大转变，从-0.133 变为-0.301 都显著，也就是说商业健康保险伴随相对保险深度增加，其负向影响也有所上升。这可能是由于随着商业健康保险在国民经济中的地位的提高，其对经济增长的作用也将受到更加复杂的因素影响。结合理论研究，在由低门槛迈入高门槛的过程中，随着商业健康保险保费和保险密度的提高，商业健康保险对经济增长的促进作用减弱。这可能是由于保费规模的增加使出险概率和损失程度都有所提高，进而对经济增长的促进作用减弱。另外，保险深度在高门槛阶段会表现出抑制经济增长的情况，这可能是由于相关免赔政策和成熟的商业健康保险市场因竞争情况发生改变以及其他多种因素共同作用导致的结果。

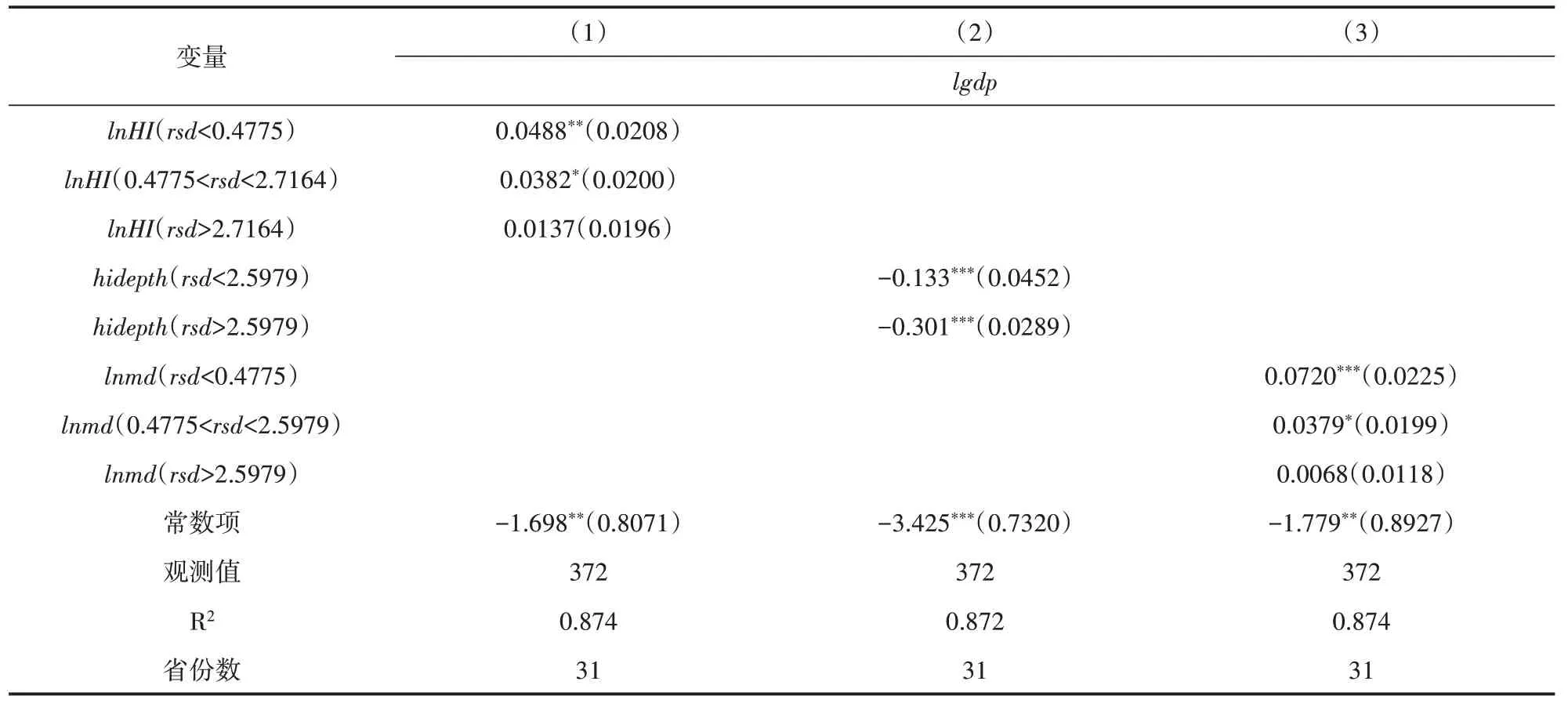
表3 商业健康保险对经济增长影响的门槛回归

2.商业健康保险对经济波动的影响

表4 的结果显示，商业健康保险的保费、保险密度与经济波动之间负相关，当跨越门槛值之后，两者对经济波动的降低程度也增加，这表明随着保费规模的扩大，商业健康保险对经济的稳定作用增强。商业健康保险的保险深度对经济波动存在显著的双重门槛效应，在低、中、高三个发展阶段，商业健康保险的保险深度对经济波动的影响系数分别为0.341、0.067 4和-0.000 984，且前两者均在1%水平上显著。这表明随着商业健康保险的保险深度的提高，经济波动幅度不断减小，商业健康保险发展到高水平阶段时能够有效地稳定经济。结合理论研究，随着商业健康保险保费规模的扩大和市场地位的提高，商业保险公司的市场把握能力更加强大，出险概率、损失程度、免赔额与市场力量参数等因素对经济的影响也不断趋于稳定。

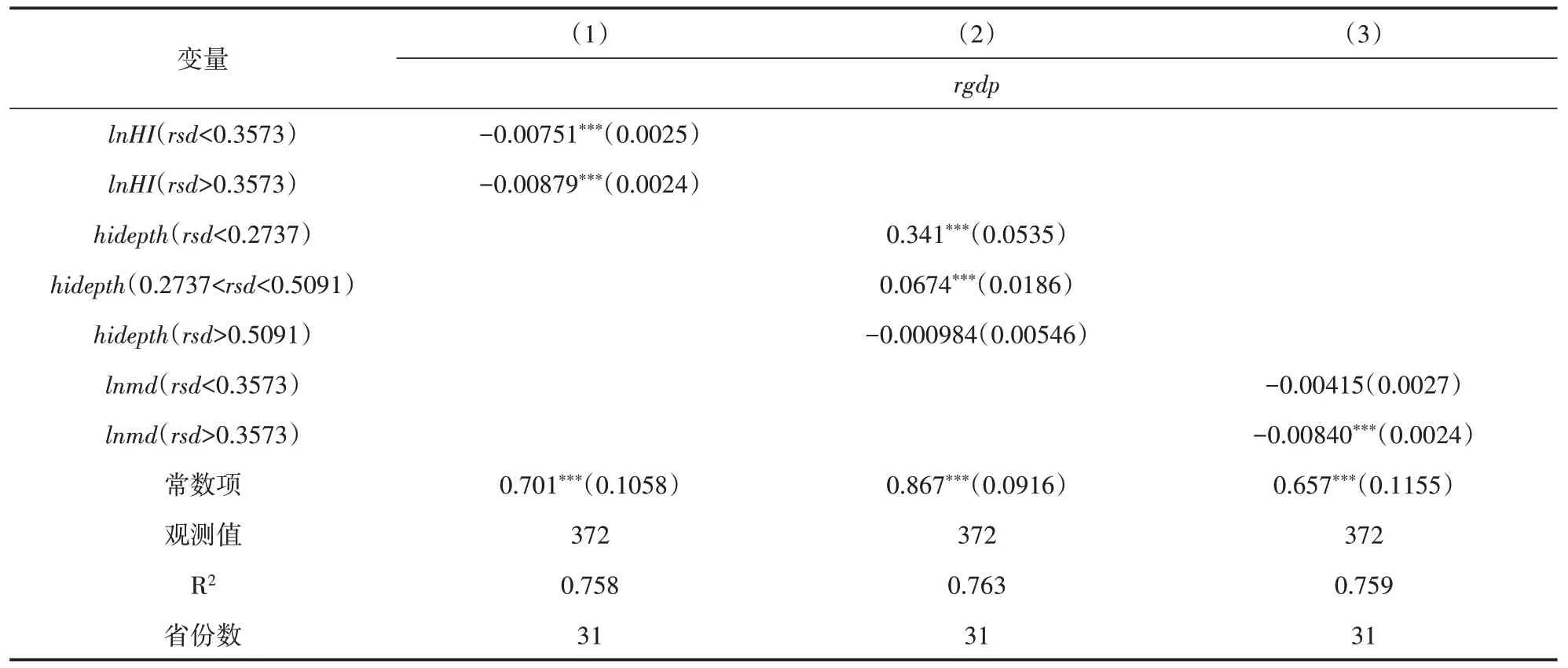
表4 商业健康保险对经济波动影响的门槛回归

（二）动态面板门槛回归

1.商业健康保险对经济增长的动态面板门槛回归

由于经济增长具有一定的持续性，因此本文采用动态面板门槛模型来检验因变量的滞后项对经济增长的影响。回归结果如表5、表6所示，经济增长的滞后项确实对经济增长产生了显著影响。在消除了经济增长滞后项的影响之后，当rsd≥0.681时，商业健康保险依旧对经济增长具有促进作用。而且商业健康保险与经济增长之间存在门槛效应，在动态面板门槛模型中，当解释变量的数值跨越了门槛值之后，商业健康保险对经济增长由负向影响转为正向影响，这表明随着商业健康保险发展水平的提高，其对经济增长的促进作用不断增强。

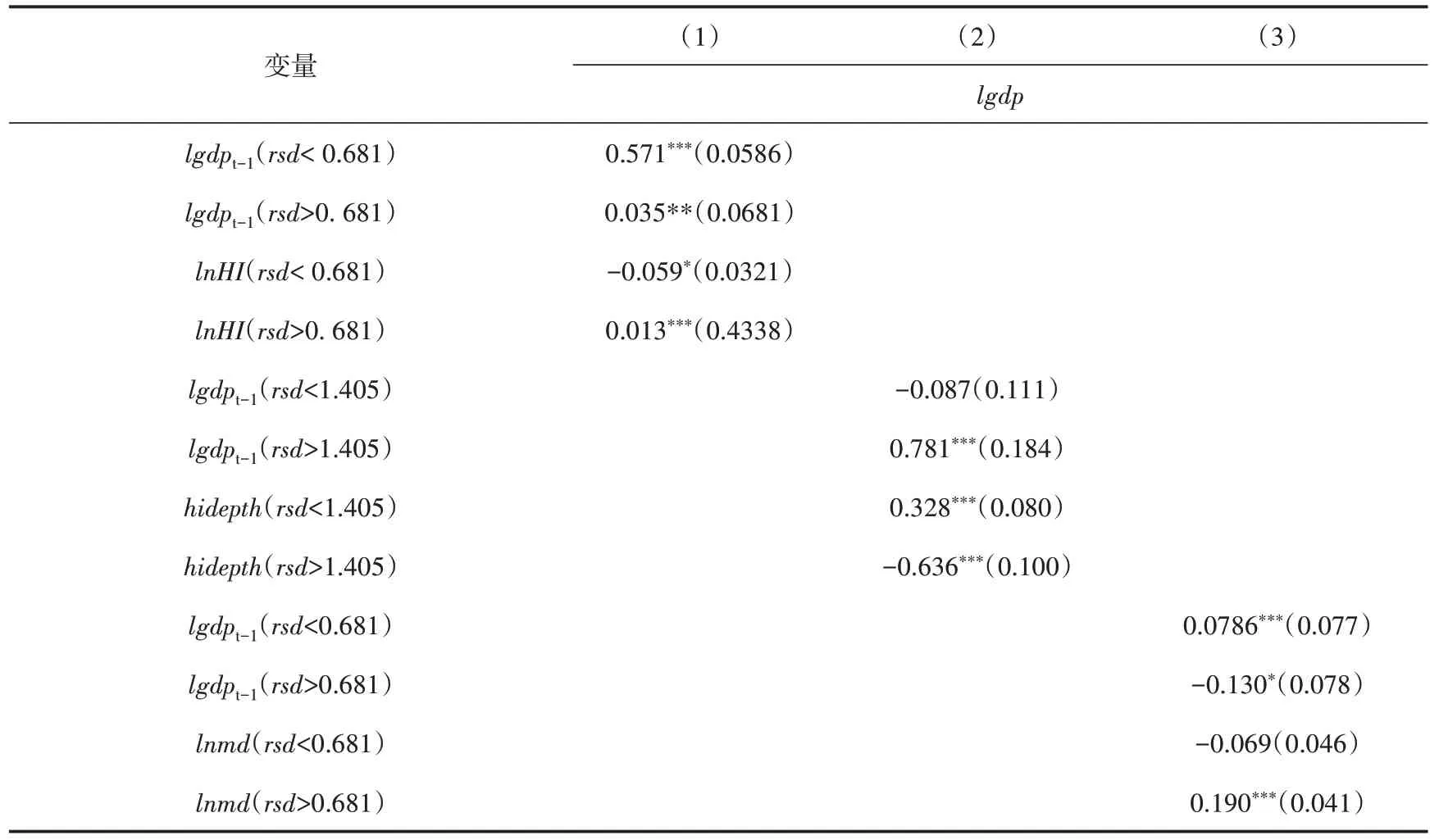
表5 商业健康保险对经济增长的基于内生面板门槛回归（动态模型）

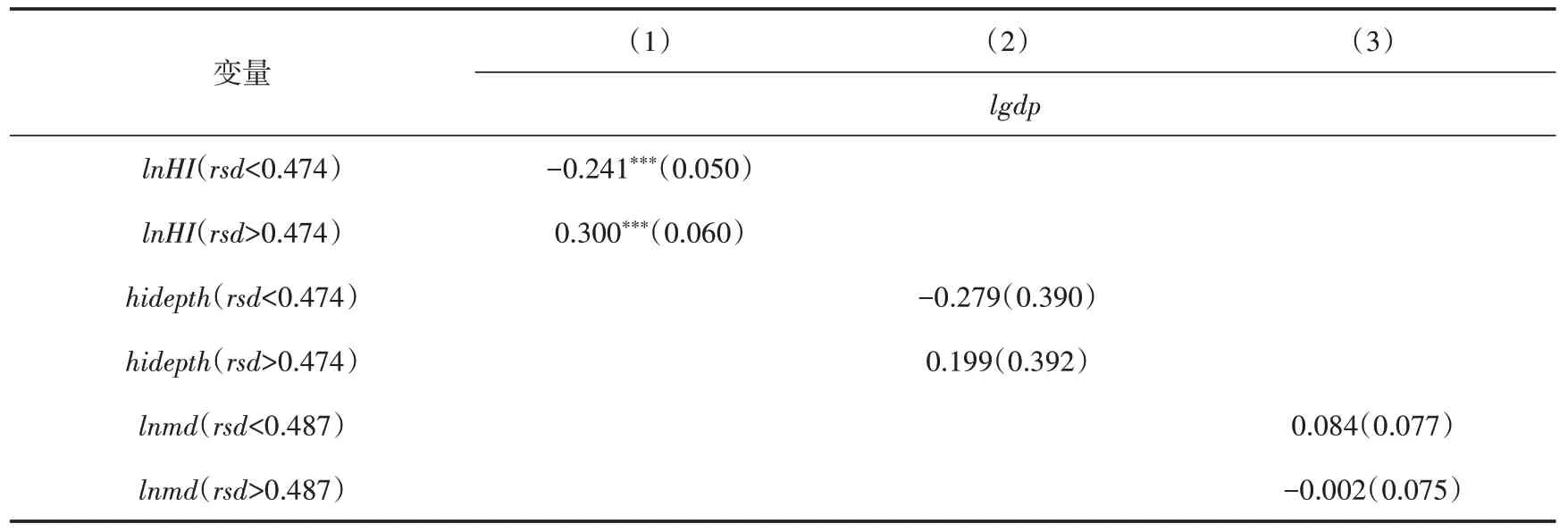
表6 商业健康保险对经济增长的基于内生面板门槛回归（静态模型）

2.商业健康保险对经济波动的动态面板门槛回归

商业健康保险对经济波动的动态面板门槛回归结果如表7、表8所示。结果表明，经济波动的滞后项对经济波动具有显著影响。在动态面板门槛模型中，在消除了经济波动滞后项的影响之后，解释变量对经济波动的影响系数比较小，而且门槛值前后影响系数的变化幅度也很小，这说明提高商业健康保险的发展水平，不仅不会对经济波动造成剧烈影响，还有利于经济的稳定。

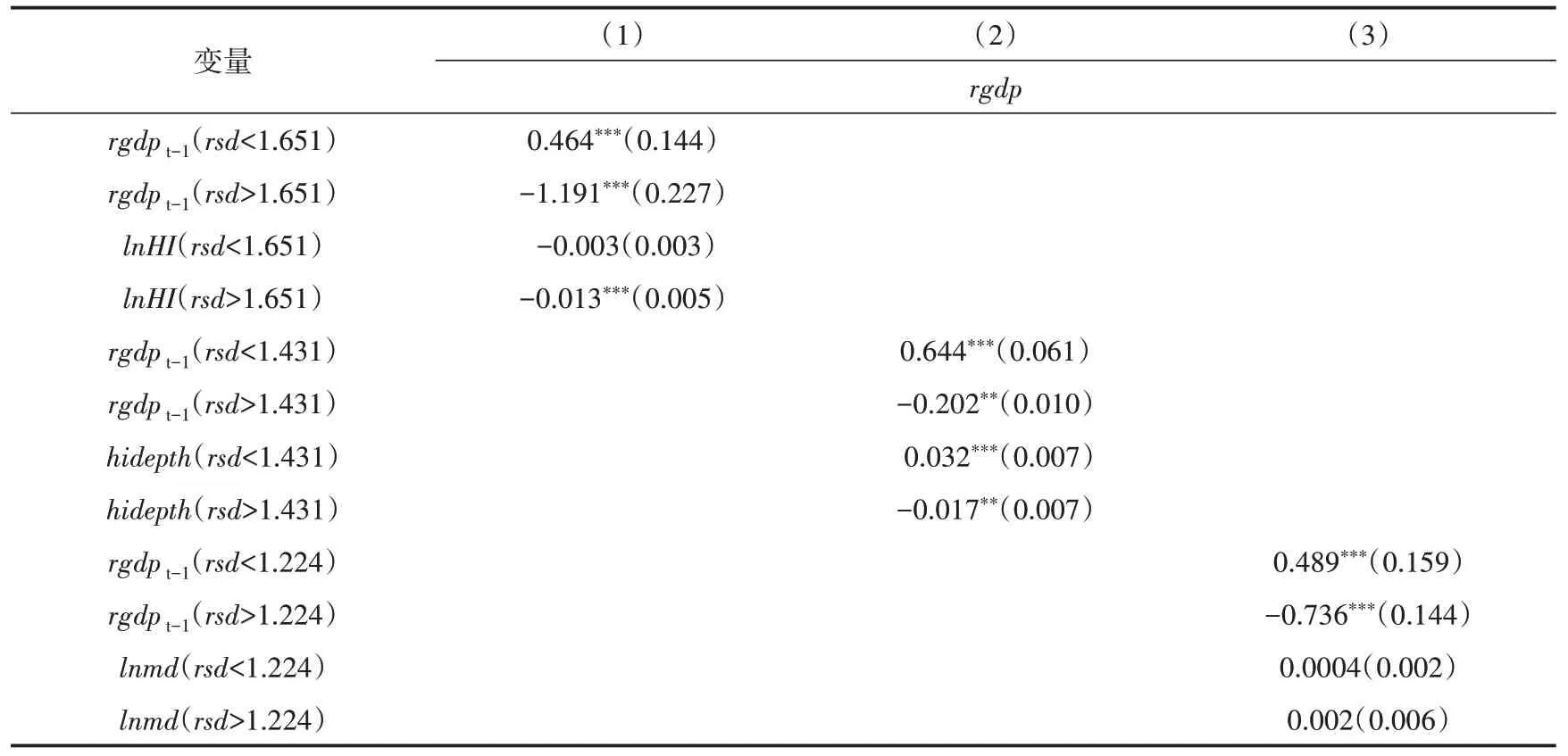
表7 商业健康保险对经济波动的基于内生面板门槛回归（动态模型）

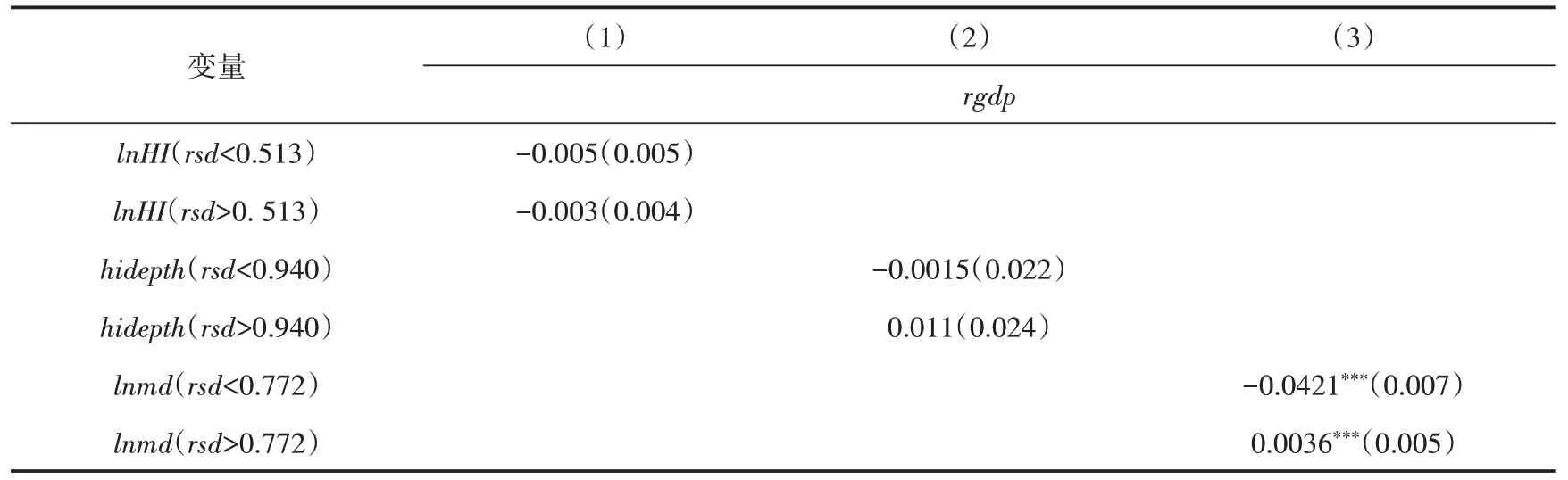
表8 商业健康保险对经济波动的基于内生面板门槛回归（静态模型）

（三）稳健性检验

商业健康保险与经济增长之间相互影响，可能存在双向因果关系，本文采用联立方程模型3SLS回归来进行稳健性检验。

1.商业健康保险、健康人力资本与经济增长的3SLS回归

表9 的结果显示，商业健康保险与健康人力资本之间是显著正相关关系，商业健康保险能够提高健康人力资本效率，而健康人力资本效率的提高也能促进商业健康保险的发展。在商业健康保险与经济增长的回归方程中，商业健康保险的保险密度和保险深度的提高都能够促进经济增长。这说明商业健康保险可能通过影响健康人力资本，进而影响经济增长。不过由于影响经济增长的因素十分复杂，同时经济增长反过来又会影响商业健康保险的发展，所以商业健康保险保费对经济增长的影响系数是负数，但是并不显著。不过代表商业健康保险发展水平的保险密度和保险深度对经济增长的影响系数是正数，这表明商业健康保险的发展是能够促进经济增长的。

表9 商业健康保险、健康人力资本与经济增长的3SLS回归

2.商业健康保险、健康人力资本与经济波动的3SLS回归

在健康人力资本方程中，商业健康保险保费、保险密度与健康人力资本显著正相关，两者均会减小经济波动幅度；而商业健康保险的保险深度则与健康人力资本显著负相关，能够加大经济波动幅度。这表明，商业健康保险可通过影响健康人力资本来影响经济波动。在表10 中，商业健康保险的保险深度是加大经济波动幅度的，但是其影响系数并不显著，这有可能是由于商业健康保险的保险深度尚未达到一个高水平发展阶段，其发展水平还没有与地区经济发展水平相匹配，同时又受到社会其他因素影响而导致的。

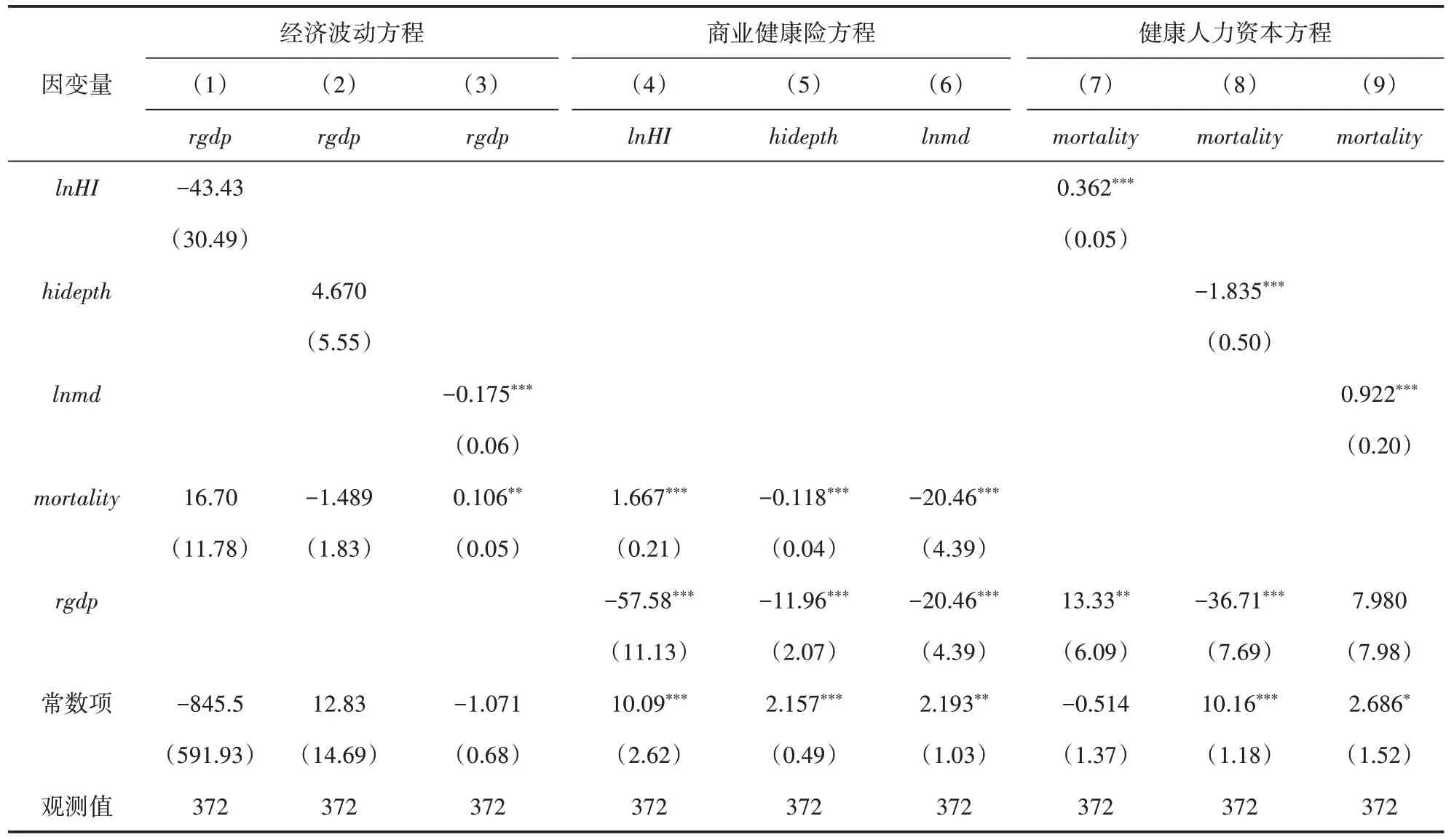
表10 商业健康保险、健康人力资本与经济波动的3SLS回归

六、结论与政策建议

本文通过引入效用函数和资产的动态，构建了一个关于商业健康保险与经济增长、经济波动之间的关系的新古典增长模型，并运用动态规划算法进行了数值模拟。理论研究表明，在影响商业健康保险保费的各种因素中，损失程度d 的提高，会同时抑制经济增长并减小经济波动幅度；免赔额度m的降低，则会促进经济增长并加大经济波动幅度；初始出险概率p 较低时会抑制经济增长并减小经济波动幅度，初始出险概率p 较高时会促进经济增长并加大经济波动幅度；初始市场力量参数m较低时会促进经济增长并加大经济波动幅度，初始市场力量参数m 较高时会抑制经济增长并减小经济波动幅度。因此，需要深入分析保费提高的结构性因素，才能分析提高保费对经济增长和经济波动产生的最终效应。

在实证分析部分，本文引用了我国31 个省份的宏观层面数据，对商业健康保险与中国经济增长、经济波动之间的关系进行了实证研究。基于面板门槛模型的回归结果表明，商业健康保险与经济增长之间存在门槛效应，提高商业健康保险的保费、保险密度和保险深度能够促进经济增长，降低经济波动。本文通过动态面板门槛模型来检验因变量滞后项和内生性问题，发现在排除经济增长和经济波动滞后项的影响之后，动态面板门槛模型的回归结果与面板门槛模型的结果基本保持一致。基于联立方程模型的3SLS 回归结果表明，提高商业健康保险的保险密度和保险深度能够促进经济增长；提高商业健康保险的保费和保险密度会降低经济波动。

基于以上研究结论，本文提出以下几点建议：

第一，结合理论研究的结论，商业健康保险保费的增加受到损失程度、免赔额度、出险概率和市场力量参数的影响。随着近些年我国经济发展水平的提高和医疗卫生条件的改善，人们的健康状况得到改善，预期寿命也在提高。在这种情况下，商业健康保险的出险概率p 和损失程度m 有可能会下降，两者的作用都是抑制经济增长和减小经济波动幅度。另外，我国保险市场发展迅速，保险公司数量不断增加，商业健康保险市场竞争日益激烈，所以市场力量参数m下降，这也会促进经济增长并加大经济波动幅度。保险经济学的一般理论认为，让个体承担一定的风险，有助于实现帕累托最优，增加全社会的福利，因此设定一个较低的合理免赔额是符合市场经济和社会福利最大化要求的。综上所述，本文建议政府鼓励商业保险公司发展惠民型的保障型健康保险产品，在满足公司经营要求的情况下，尽可能地扩大可保责任，同时适当降低免赔门槛。发展此类保障型健康保险产品，一是可以为公司增加保费；二是参保人数增加可以分散风险；三是能体现出保险公司的社会责任，帮助保险公司树立良好的企业形象，从宏观层面促进我国经济增长，增加全社会福利。

第二，实证研究结果表明，提高商业健康保险的保险密度和保险深度能够促进经济增长并减小经济波动幅度。因此，国家应大力支持商业健康保险发展，同时为企业发展营造一个良好的经商环境。另外，在商业健康保险发展前期，可以以增加保费和扩大商业健康保险市场规模为目标，提高商业健康保险的保险密度，从而促进我国经济增长。当商业健康保险发展到一定程度时则要转变发展方式，使商业健康保险的发展与经济发展水平相适应。这个阶段应当以增加健康保险产品服务为主，增强商业健康保险与其他产业如医药医疗、养老等产业的联系，提高商业健康保险的保险深度，从而起到促进经济增长并平稳经济的作用。