破产概率视角下的巨灾保险偿付能力分析——基于混合分布模型

巢 文，钱晓涛

（1.福建理工大学 管理学院，福建福州 350118；2.福建理工大学 计算机科学与数学学院，福建福州 350118）

一、引言

我国幅员辽阔、地形复杂且气候多变，是世界上自然灾害数量最多、受影响最严重的国家之一。民政部门有关资料表明，我国每年因自然灾害造成的直接经济损失为500亿元～600亿元，折合每天损失额高达1亿多元［1］。

巨灾保险是分散巨灾风险的重要手段。2017年，原中国保监会在全国范围内加速推进《建立城乡居民住宅地震巨灾保险制度实施方案》，积极开展地震巨灾保险地方试点，探索研究覆盖地震、台风和洪水等主要自然灾害的巨灾保险制度。然而，由于我国整体上巨灾风险防范意识淡薄，资本市场发展缓慢，加上受巨灾风险分散技术的限制，巨灾保险在我国分散巨灾风险的作用十分有限。面对巨灾，我国目前主要采用行政手段进行救助，政府为此承担了沉重的补偿责任。为了减轻政府财政负担、确保国家财政体系稳定运行，探寻建立一个适合我国国情的巨灾保险制度体系势在必行。为此，本文从破产概率的视角分析保险公司的巨灾保险偿付能力，不仅对保险公司稳健经营具有重要的现实意义，而且有利于建立和完善我国巨灾保险制度体系。

破产概率是评估保险公司风险偿付能力的一个重要数量指标。GERBER［2］和FELLER［3］使用随机过程来刻画保险公司的盈余，并分别利用鞅方法和更新理论得到了保险公司风险模型破产概率的显式表达式。在破产概率最小化的目标下，YANG和ZHANG［4］通过求解HJB 方程，获得了保险公司的最优投资策略。WUTHRICH 和MARIO［5］从破产概率的视角，评估了多个因素对非寿险公司保险偿付能力的影响。当索赔额服从轻尾分布时，闫德志［6］给出了破产概率的显式表达式。

然而，当承保险种的索赔额服从重尾分布时（如地震、台风和洪灾等巨灾保险），保险公司的破产概率没有显式表达式，此时只能讨论其数值模拟解［7］或者渐近结果［8-12］。刘昕龙等［7］应用Monte Carlo 模拟法测算了巨灾保险共同体的巨灾风险转移效率与破产概率。LI［10］利用控制收敛定理给出了有限时间内风险模型破产概率的尾渐近估计。尚勤和李隆鑫［12］运用Peaks over Threshold（POT）模型拟合我国地震直接经济损失数据，通过超额均值函数法（Mean Excess Function，MEF）和Hill 图法确定POT模型中的阈值，进而利用破产概率渐近结果分析了保险公司的巨灾保险偿付能力。

与已有文献相比，本文的创新点主要体现在：①用非参数核密度估计方法拟合巨灾损失的截尾数据，用广义帕累托分布拟合巨灾损失的尾部数据，从而构建了一种拟合巨灾损失的混合分布模型。②基于混合分布模型，考虑了对巨灾造成的所有直接经济损失都按比例进行保险偿付的情形，给出了其破产概率的尾渐近估计，再以此评估保险公司对巨灾风险的偿付能力，弥补了已有研究仅对超出阈值部分的损失进行偿付能力分析的不足。③应用峰度法确定混合分布模型中的阈值，避免了使用MEF图和Hill图法所造成的主观判断误差。

二、混合分布模型的构建

设保险公司在t时刻的盈余过程U(t)为：

其中，x≥0为公司的初始资本；c＞0表示单位时间内保费收入率；0 ＜k＜1 为损失赔付比例；N(t)表示在[0,t]内巨灾发生的次数，服从参数为λ＞0 的Poisson 过程；{Yi,i≥1} 表示第i次巨灾造成的经济损失，是一列独立同分布的非负随机变量，其共同分布函数为FY(·)且与{N(t),t≥0} 相互独立。

记T=inf{t:t≥0,U(t) ＜0} 为保险公司的破产发生时刻，于是在初始资本为x的条件下保险公司的破产概率可表示为：

（一）广义帕累托分布

广义帕累托分布（Generalized Pareto Distribution，GPD）可用于研究样本超出量的分布特征，现已被广泛地应用于巨灾尾部风险的研究［13-16］。GPD 将所有超出阈值u的巨灾损失数据y1,y2,…,yNu作为观测样本，其中Nu表示超出阈值的样本数。

由损失变量Y的分布函数为FY(y)，有超出量Y-u的分布函数：

因此，当Y≥u时，有

根据PBdH（Pickands-Balkama-de Hann）定理［17］，当阈值u足够大时，超出量分布函数Fu(y)可以用GPD近似：

其中，ξ＞0 是形状参数，σ＞0 是尺度参数。当ξ＜1 时，GPD 的均值为，否则GPD 的均值不存在。

（二）混合分布模型

由于GPD 仅拟合了巨灾损失超过阈值u的尾部数据，本文为此再寻找一个新的分布来拟合低于阈值的截尾数据，即建立混合分布模型来刻画巨灾损失。对截尾数据的主体分布拟合通常有参数方法和非参数方法。参数方法是假定总体服从某种已知的分布，即密度函数已知，再由样本估计其中的参数，显然该方法依赖事先对总体分布的假设，非参数方法则避免了主观假设总体分布的问题。因此，本文选择非参核密度估计方法来拟合巨灾损失截尾数据。

记支撑集为[0,u]的核密度估计为：

其中，n为样本容量，h为窗宽，K为核函数。已有的许多研究成果表明，Epanechnikov 核是最佳的核函数，因此在实证分析中本文也是采用该核函数，其表达式如下：

其中，I(·)为示性函数，当 ||x≤1 时，I(||x≤1)=1，否则I(||x≤1)=0。

综合（2）式、（3）式和（4）式，损失变量Y的混合分布函数FY(y)可表示为：

三、基于混合分布模型的破产概率

定理1 若损失变量Y的混合密度函数为（5）式，则风险模型（1）的破产概率满足尾渐近估计：

证明：记Z=kY。众所周知，GPD 是次指数分布。因此，应用EMBRECHTS P 和VERAVERBEKE N的研究成果［18］，我们有

另一方面，又有

将（8）式和（9）式代入（7）式，则定理1得证。

四、实证分析

（一）数据描述

本文以我国大陆地区1990—2018 年震级5 级以上地震的直接经济损失为研究样本，主要数据来源于《中国统计年鉴》《中国古今地震灾情总汇》和《中国大陆地震灾害损失评述》［19-24］的相关文献。由于原始数据中各年份的损失值均为当年实际经济损失，为了保证各年份之间的数据具有可比性，需要消除通货膨胀的影响。因此，本文以2018 年为基期，采用GDP 调整法对历年的地震直接经济损失进行调整。从表1 可以看到，样本数据的标准差很大，偏度为9.52，峰度达到114.93。这说明数据右偏，具有明显的“尖峰厚尾”特征，适合用GPD等重尾分布刻画其尾部。

表1 地震直接经济损失（万元）的基本描述性统计

（二）阈值选取

阈值的选取很重要，如果阈值太大，会导致超过阈值的数据太少，使得GPD 的参数估计值过大，还可能导致模型在估计过程中存在不收敛现象。如果阈值太小，样本的超阈值不能满足渐进服从GPD的性质。

现有文献大都采用MEF 和Hill 图法来选取阈值u。对给定的样本(y1,y2,…,yn)，MEF 图法定义了经验平均超越值函数：

对于某个阈值u0，超出量Y-u0的分布近似服从GPD，则en(u)呈线性变化。因此，可以通过观察en(u)关于u的图像何时近似为线性来选取阈值。从图1可以看到，图形大致在u＞240 000后是近似线性的，所以按照MEF 方法，应选取240 000 为阈值。

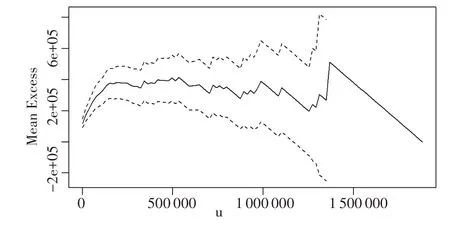
图1 平均超越值函数图

设y(1)＜y(2)＜…＜y(n)是样本的次序统计量，则尾部指数Hill统计量为：

Hill 图法在平面直角坐标系上，以(m,)为点坐标绘制曲线。通过观察曲线的稳定区域，以其起点的横坐标选作阈值。由图2 可见，阈值u大约取77 000 之后的Hill统计值在尾部区域保持平稳，因此根据Hill图法，应令阈值为77 000。

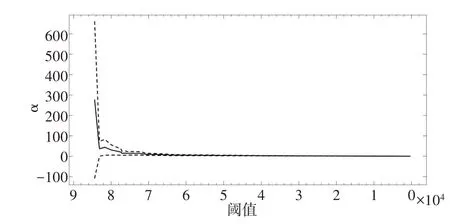
图2 Hill图

显然，上述两种方法通过观察图像的大致变化特征来进行阈值选取，存在较强的主观性，特别是对数量级差别较大的巨灾损失数据，这种主观判断往往会造成很大的偏差。为了克服上述方法的不足，PATIE［25］提出了峰度法，利用正态分布峰度系数等于3 的条件，通过正态分布与偏态分布的交点来确定阈值，具体步骤如下：

第二步，比较样本峰度和正态分布峰度，如果Kn≥3，则将使||-yi取值最大的yi从样本中剔除；

第三步，重复第一步和第二步，直至样本峰度Kn＜3；

第四步，将剩余样本中最大的 ||yi选为阈值。

根据以上步骤，运用Matlab软件编写峰度法程序，可得阈值u=87 468，共有83 个数据超过阈值，即Nu=83。

（三）参数估计与拟合检验

首先，采用最大似然估计法对GPD 中的参数ξ和σ进行估计。对（3）式求导后可得GPD 的概率密度函数：

其次，对核密度估计中的窗宽h进行选取，其取值的大小会影响到的光滑性。如果h取值较大时，将有相对较多的样本点对y处的估计值产生影响，而且距y较远的点和较近的点所对应的估计值也将比较接近，此时fh(y)图像表现为光滑曲线，但同时也将丢失样本数据所包含的一些信息。反之，如果h取值较小时，将有相对较少的样本点对y处的估计值产生影响，而且距y较远的点和较近的点所对应的估计值也将比较疏远，此时图像表现为不光滑折线，但能反映出更多样本数据所包含的信息。因此，选取合适的窗宽是核密度估计方法的一个关键步骤。

借鉴已有相关文献的做法，定义积分均方误差（mean integrated squared error，MISE）为关于窗宽h的函数：

其中，f(x)为总体的真实分布密度，通常可用正态分布近似。当样本容量n较大时，有

求解的最小值点，可得最佳窗宽的估计值：

利用Matlab 统计工具箱中所提供的ksdensity函数可求得=0.734 5。

最后，检验混合分布对直接经济损失的拟合效果。图3 显示了核密度估计分布对经验分布的拟合效果图和QQ 图。可以看到，核密度估计分布与经验分布拟合效果较好，且QQ 图几乎呈45 度直线，这说明核密度估计可以较好地拟合地震直接经济损失的截尾数据。图4 显示了GPD 对经验分布的拟合效果图和QQ 图。可以看出，GPD 与经验分布拟合效果良好，而QQ 图除了右上角有一个点有所偏离外，其他点几乎呈45 度直线。需要指出的是，该异常值是由2008 年汶川特大地震造成。综上可知，GPD也可以较好地拟合地震直接经济损失的右尾数据。

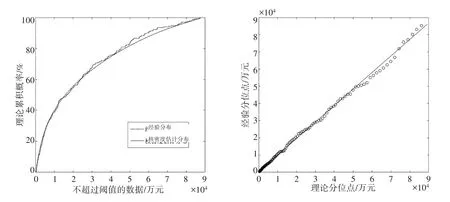
图3 经济损失截尾数据的经验分布与核密度估计分布的比较

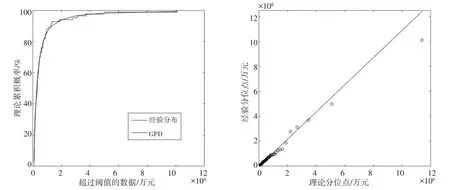
图4 经济损失右尾数据的经验分布与GPD的比较

（四）破产概率视角下的巨灾保险偿付能力分析

令保险公司的初始资本x=1 000亿元；为了吸引更多人投保，相对安全系数不宜设置过高，令θ=0.1；参照我国保险公司在巨灾损失赔付中的实际情况，令赔付比例k=0.02，用经验分布函数估计，故；将四（三）节中的参数估计结果全部代入（6）式，并用Matlab 计算核密度积分的数值解，最后得到保险公司的破产概率ψ(x)=15.39%。

为了进一步确定各参数对偿付能力的影响程度，本文分别对偿付比例、相对安全系数和阈值进行敏感度分析。

1.从图5 可以看出，随着偿付比例k的提高，破产概率增大。当偿付比例固定时，破产概率随初始资本的增大而下降。如果我国将偿付比例提高到较高的20%，在初始资本为1 000亿元的条件下，破产概率将迅速从15.39%增加到38.26%。为了让保险公司的巨灾保险偿付能力保持一个较高的水平，可以通过给保险公司注入更多的初始资本来实现。这就需要扩大投保规模，或借助资本市场发行巨灾债券等方式变相增加初始资本。

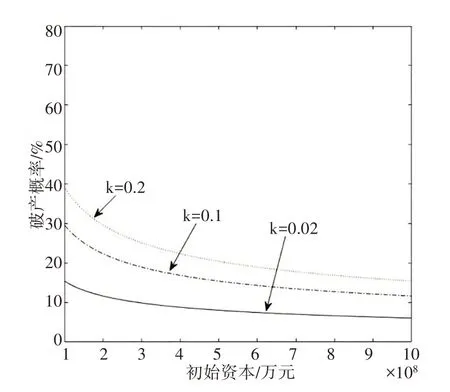
图5 θ=0.1时的破产概率敏感度分析

2.从图6 可以看出，随着相对安全系数θ的增大，破产概率下降。当相对安全系数固定时，破产概率仍呈现出随着初始资本增大而下降的规律。此外，对比图5和图6可见，破产概率对相对安全系数的敏感度要高于偿付比例。这表明保险公司通过提高相对安全系数可以更有效地增强偿付能力。然而，提高相对安全系数，意味着人们要为巨灾保险支付更高的保费，而提高保费这种做法将会导致保险公司的保险业务不断流失，不能从根本上降低巨灾保险的偿付风险，因此保险公司不能过分依赖增加保费的方式。

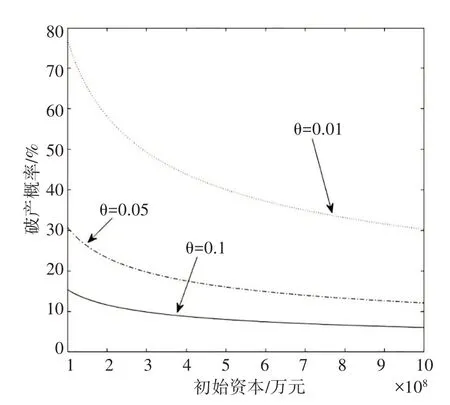
图6 k=0.02时的破产概率敏感度分析

3.为分析不同阈值对破产概率估计值的影响，图7 以峰度法所确定的阈值u=87 468 为基准，与前文MEF和Hill图法所确定的阈值进行比较，都用最大似然法重新估计模型中的各个参数，进而描绘了不同初始资本下破产概率估计值的变动比例。可以看到，阈值的变化对破产概率的估计结果有着显著的影响，如果忽视阈值的选取将严重影响破产概率估计的准确性。因为MEF 和Hill 图法是通过主观观察图形变化来选择阈值的，当样本数量级较大时，这两种方法难以得到拟合效果较好的阈值，这也说明了本文在巨灾数据建模研究中应用峰度法来客观确定阈值的必要性。

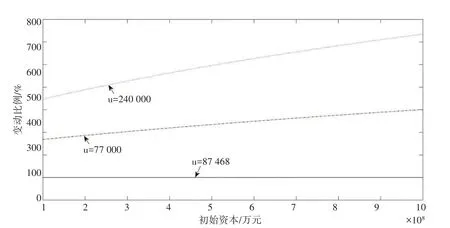
图7 阈值变化对破产概率估计值的影响

五、结语

近年来，巨灾造成的经济损失愈发严重，迫切需要开展巨灾风险补偿工作。保险作为社会稳定器，在发挥化解巨灾风险和损失补偿的功能方面，具有不可替代的作用。本文构建了巨灾损失数据的混合分布模型。在该模型中，先利用峰度法确定阈值，再用非参数核密度估计拟合低于阈值的截尾损失数据，并用GPD 拟合超过阈值的尾部损失数据。在理论模型构建的基础上，选取我国1990—2018 年震级5 级以上地震灾害损失数据进行了实证分析。结果表明：

第一，一方面，增加保险公司的初始资本可以有效降低保险公司的破产概率，从而增强其巨灾保险的偿付能力；另一方面，提高相对安全系数虽然可以增强偿付能力，但会造成保险业务流失，因此保险公司不能过度依赖提高保费的方式。为了充分发挥保险的社会稳定器作用，将我国的巨灾保险偿付比例逐渐提高到发达国家水平，需要政府加大对保险公司的支持力度，如对开展巨灾保险业务的保险企业实行税收优惠政策；加大宣传，引导更多居民购买巨灾保险，从多方面扩大保险企业的资本规模，以增强其巨灾保险的偿付能力。

第二，阈值选取对破产概率的估计有显著影响，在对巨灾损失数据进行建模分析时需要特别注意阈值选取的准确性。本文利用峰度法定量选取阈值，克服了用MEF图和Hill图定性选取阈值的缺陷，有效保证了阈值选取的准确性。

第三，本文所构建的混合分布模型对巨灾损失数据的拟合效果良好，可以为我国建立巨灾保险制度提供理论参考，有利于进一步开拓巨灾保险市场，增强我国巨灾保险市场承保巨灾风险的能力。