连续管防喷盒胶筒摩擦机理及过管稳定性分析*

郑 翔 陈 婷 曾永锋 朱再思 邓 琳 李 伟 郭 伟

(1.中石油江汉机械研究所有限公司 2.长江大学机械工程学院 3.中国石化工程建设有限公司)

0 引 言

连续管技术具有作业安全、效率高等优势，在页岩气开采中的应用越来越广泛。目前，我国页岩气开采井况呈现出井深增加、井内压力增大的趋势，井控设备的性能直接影响连续管作业的安全性[1-2]。防喷盒安装在注入头下方，隔离井筒内流体，是连续管作业井控安全的关键[3-4]。防喷盒的核心密封件为胶筒，在外部液压力和井内介质压力的共同作用下，胶筒与连续管接触形成密封。如果连续管与胶筒之间的摩擦力过大，则会加剧密封面磨损，缩短胶筒的使用寿命。密封失效会造成井内流体溢出，危害人员安全，污染环境[5]。

学者们针对连续管防喷盒的研究主要包括结构改进和失效分析。2008年，陈澈等[5]对连续管防喷盒失效原因进行了分析，提出了正确的操作和维护方法。2013年，朱兆亮等[6]将连续管防喷器胶筒的几何形状由等直径胶筒改为鼓形，并采用双胶筒结构，改善了胶筒端部受力集中的现象，增强了胶筒密封性能。2017年，刘远波等[7]改进了FB13-70连续管防喷盒密封结构，拓宽了防喷盒适应连续管管径的范围。但是，当前研究连续管过防喷盒胶筒的摩擦阻力及摩擦阻力对井口连续管径向无支撑段稳定性影响的报道不多。

连续管由低碳合金钢制造，具有尺寸小、柔性大、易发生失稳、加压困难等特点[8-9]。目前，计算注入或起升连续管时的轴向力往往忽略连续管过防喷盒的摩擦阻力或将其作为一个常数[8，10-13]，不能准确得到连续管轴向力。另外，依据注入头的结构，当连续管离开注入头夹持块至防喷盒导入口时处于径向无支撑状态。随着作业深度的增加，井筒内流体压力增大，需增加连续管与胶筒间接触压力以保证井口密封，这样会导致连续管过防喷盒的摩擦阻力增大，连续管轴向力随之增大。当该轴向力过大时，无支撑段连续管存在失稳甚至折断的风险[10-11]。因此，分析连续管过防喷盒时各因素对其摩擦阻力影响规律及其对井口连续管无支撑段稳定性的影响十分必要。基于此，笔者通过分析防喷盒胶筒的摩擦磨损机理，采用有限元方法建立连续管过防喷盒的摩擦接触有限元模型，并基于二次开发方法，利用Python语言编写脚本访问有限元计算结果文件，运算后得到连续管摩擦力；同时研究不同的运动速度、摩擦因数和井筒介质压力对防喷盒胶筒摩擦力的影响规律，并对不同参数下连续管无支撑段最大允许长度值进行计算。所得结论可为优化作业参数和计算连续管无支撑段最大允许长度提供理论基础。

1 密封原理及摩擦分析

防喷盒的密封原理是在外部液压控制压力p1和井内流体压力p2的共同作用下，胶筒与连续管接触，直到胶筒与缸套、连续管间的摩擦力等于外部液压控制压力p1和井内流体压力p2的合力时形成密封。防喷盒密封原理如图1所示。胶筒的结构多为双瓣式半球齿面啮合。连续管注入或起出井时需穿过胶筒，胶筒密封面因与连续管摩擦而发生磨损。通过现场及文献调研可知，胶筒的主要失效形式是磨损失效[11]。

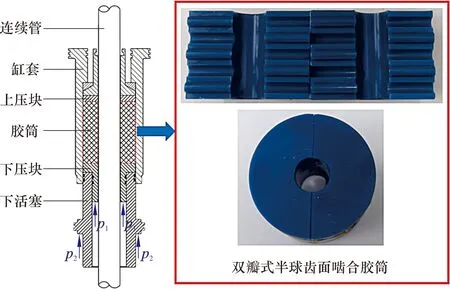
图1 防喷盒密封原理图Fig.1 Schematic diagram for sealing of stripper

图2为油田现场收集的2个防喷盒胶筒。由图2可知，胶筒上下两端磨损严重，且上端具有明显的撕裂、掉胶现象。为了进一步分析胶筒与连续管间的摩擦磨损机制，利用超声波清洗机及无水乙醇对胶筒进行清洗，应用奥斯微(AOSVI)高倍数码电子显微镜观察表面微观磨损形貌，放大倍数为80，相关设备及结果如图3所示。由图3可知，胶筒与连续管的接触面上沿相对滑动方向出现了大量犁沟状磨痕。这是由于连续管材料硬度远大于胶筒材料硬度，且连续管这类井下作业管柱表面粗糙度较大，可达15 μm。当胶筒与连续管接触且发生相对运动时，连续管表面粗糙微凸体切削(微切削)胶筒表面，形成深度与宽度不同的犁沟。胶筒的主要磨损形式是磨粒磨损，其摩擦力产生的主要因素为机械作用力[14-15]。

图2 使用过的防喷盒胶筒Fig.2 Used strippers

图3 电子显微镜及结果Fig.3 Electron microscope and results

2 摩擦阻力计算及结果分析

2.1 接触有限元分析

依据连续管注入头配套的防喷盒结构及其密封原理，利用ABAQUS软件建立连续管过防喷盒的有限元模型，具体模型如图4所示。胶筒材料选用力学性能优异、耐磨和耐油的聚氨酯[15-17]，邵氏硬度为85 HS；材料模型选择Mooney-Rivlin模型[18-19]，C10=2.101，C01=0.105。模型各部件属性、尺寸及网格数量、类型如表1所示。胶筒几何结构不规则，对胶筒划分网格时，先对胶筒模型进行切分，再采用结构化网格(图4b绿色区域)和扫略网格(图4c黄色区域)划分技术，网格划分算法为中性轴算法，胶筒模型切分及网格如图4b和图4c所示。

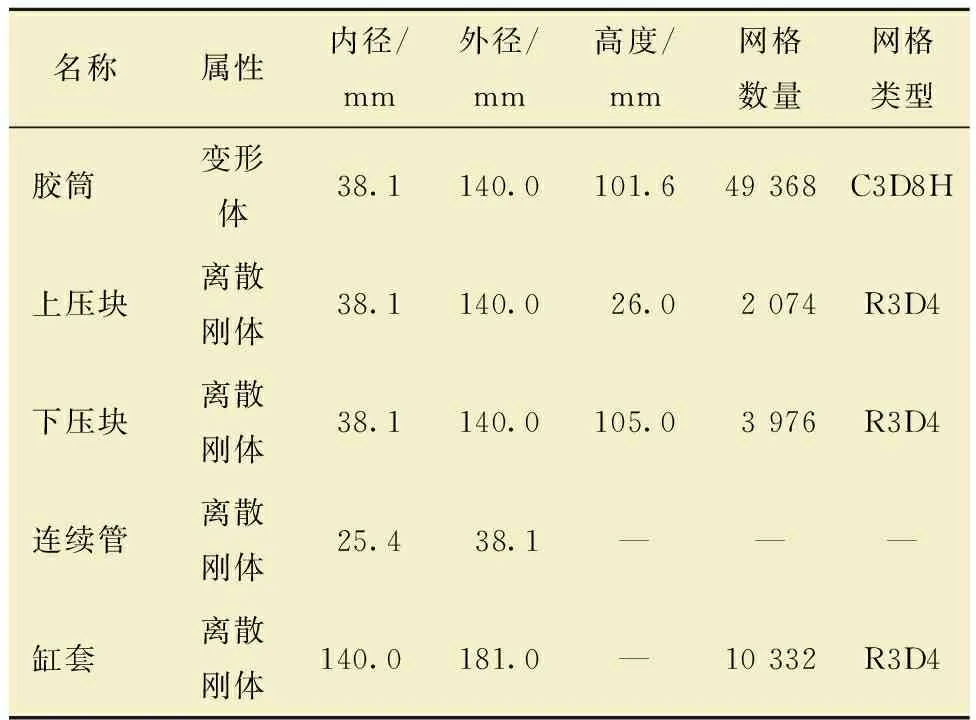
表1 模型各部件属性、尺寸及网格参数Table1 Attributes，dimensions and grid parameters of components in the model

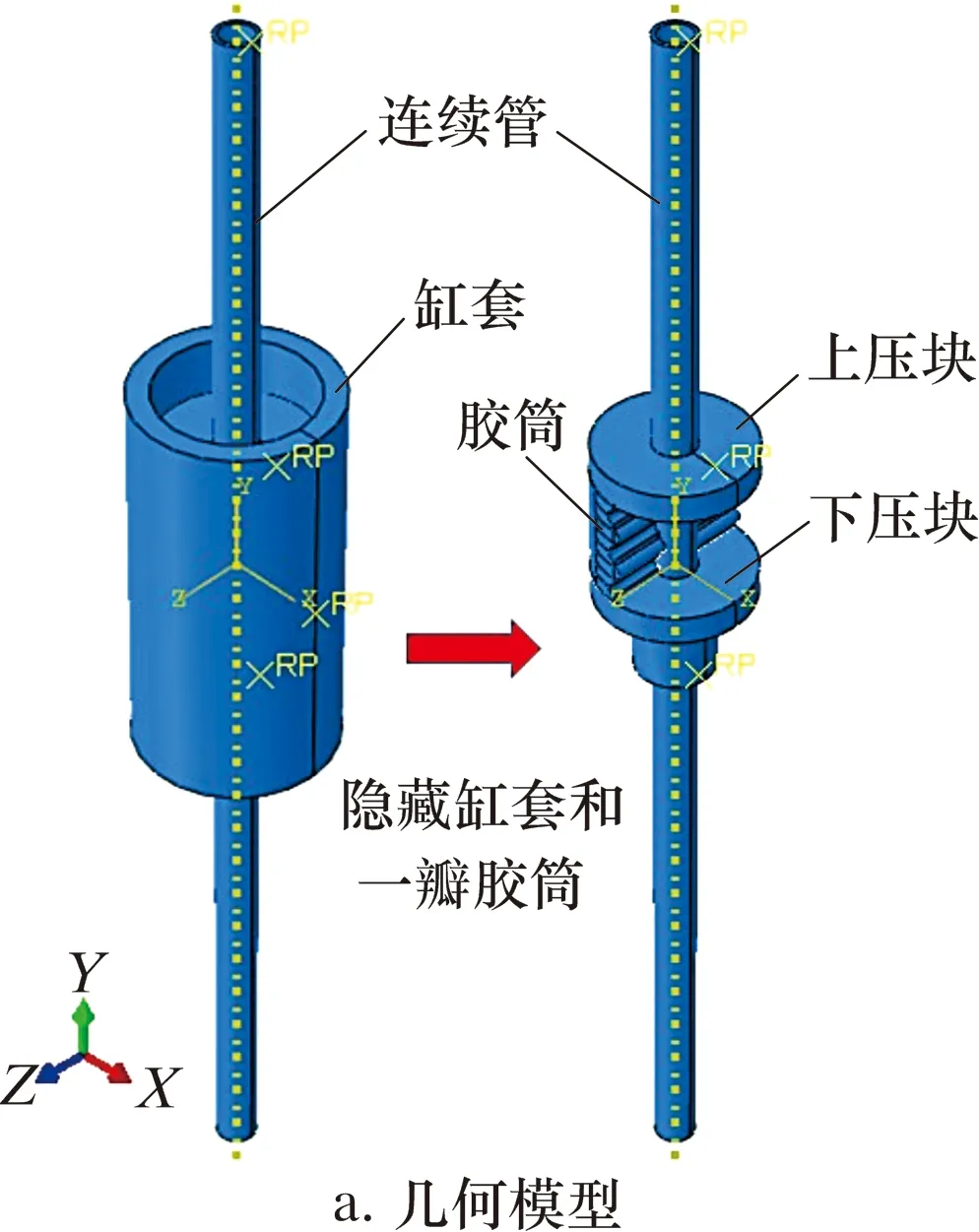
模型中各部件接触关系具体设置参照文献[4]，采用罚函数法施加无穿透接触约束，使产生接触的2个物体满足无穿透条件；摩擦模型(切向作用)选择库仑摩擦模型，以摩擦因数来表征接触面间的摩擦学特性[20-22]。作业时受流体、泥沙和油污等井内介质的影响，连续管与胶筒接触界面摩擦学系统处于复杂的混合/边界润滑状态，摩擦因数处于0.01～0.40之间，其他接触对的摩擦因数如表2所示[16，23-30]。

表2 接触对间的摩擦因数Table2 Friction factor between contact pairs

边界条件设置：上压块、上活塞套全约束，连续管和下压块可沿Y轴方向移动。控制系统压力和井筒介质压力作用在下压块的参考点上。连续管沿Y轴正方向运动模拟注入头起升连续管，连续管沿Y轴负方向运动模拟注入头注入连续管[4]。

2.2 摩擦阻力计算方法

连续管过防喷盒摩擦力主要为防喷盒胶筒所受的摩擦力，计算式为：

Ff=μF

(1)

式中：Ff为摩擦阻力，N；F为胶筒与连续管接触面上的接触力，N；μ为摩擦因数，无量纲。

防喷盒胶筒与连续管接触面为曲面，如图5所示。

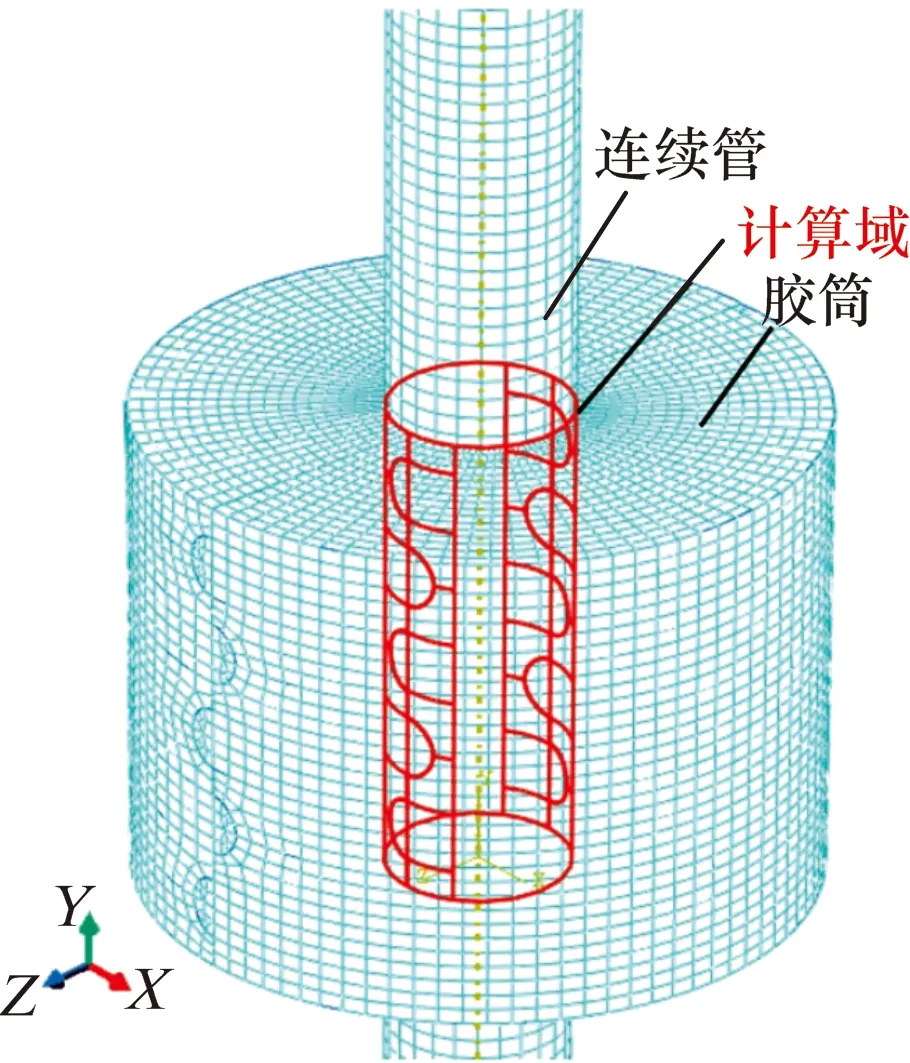
图5 胶筒与连续管接触示意图Fig.5 Schematic diagram for contact between stripper and coiled tubing

接触力F无法直接由ABAQUS软件输出，F计算式为：

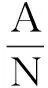
(2)

式中：p为从面上所有接触节点的接触压力之和，MPa；A为从面的面积，mm2；N为从面上节点数。

由图5可知，假设从面上所有节点都与主面发生接触，图5中红色区域为计算域。胶筒所受摩擦力的具体计算步骤：基于ABAQUS计算结果，利用Python语言二次开发脚本程序提取计算域节点的编号和接触应力，并得到计算域的节点总数和所有节点的接触压力之和；依据胶筒的结构可计算从面的面积，具体计算流程如图6所示。计算域内总节点数为3 564，计算域的面积为12 154.81 mm2。

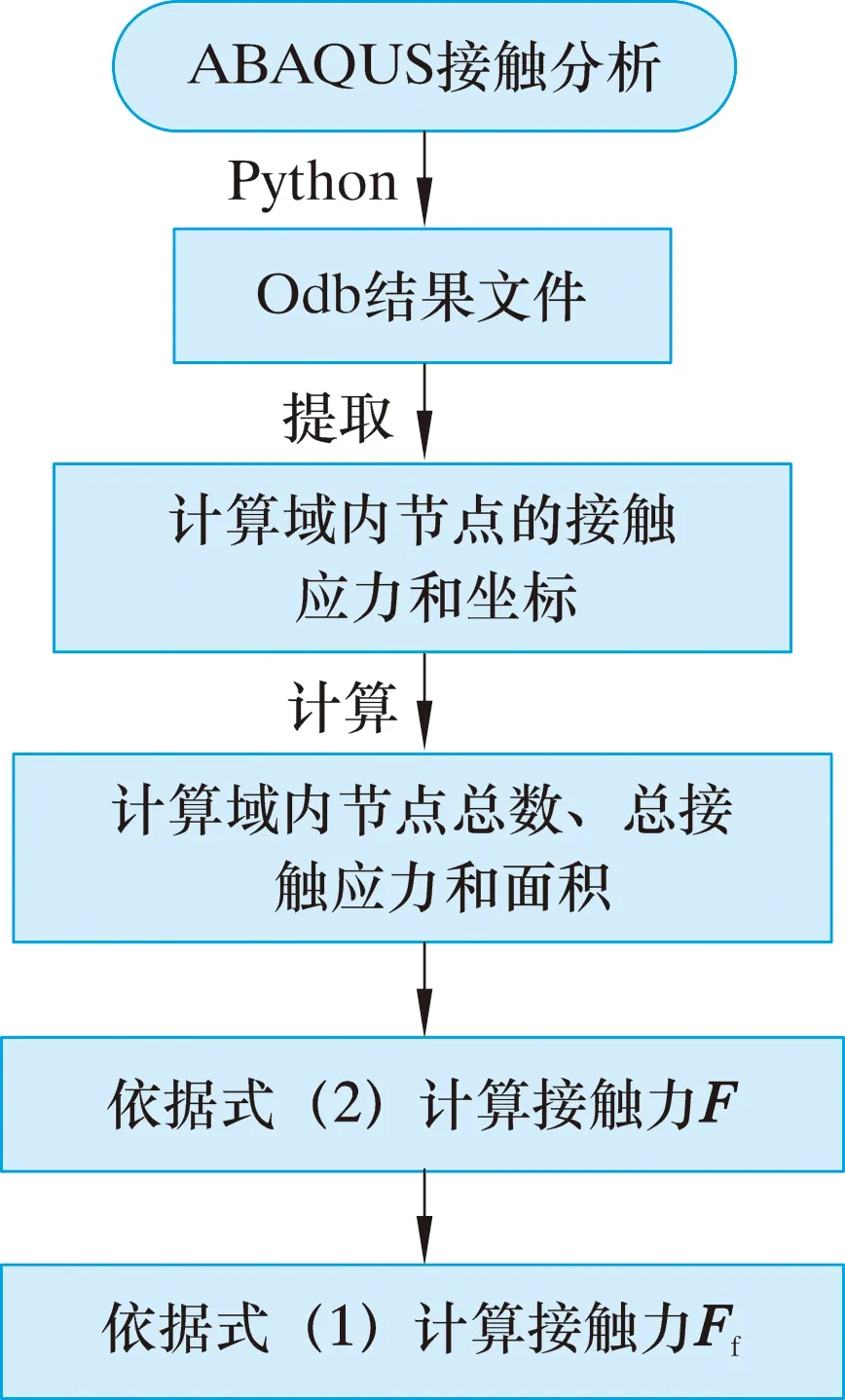
图6 摩擦阻力计算流程图Fig.6 Flowchart for calculation of friction resistance

2.3 结果分析

2.3.1 有限元模型可靠性验证

当连续管静止且井筒介质压力为70 MPa、连续管与胶筒之间摩擦因数为0.10时，胶筒的应变能密度如图7所示。

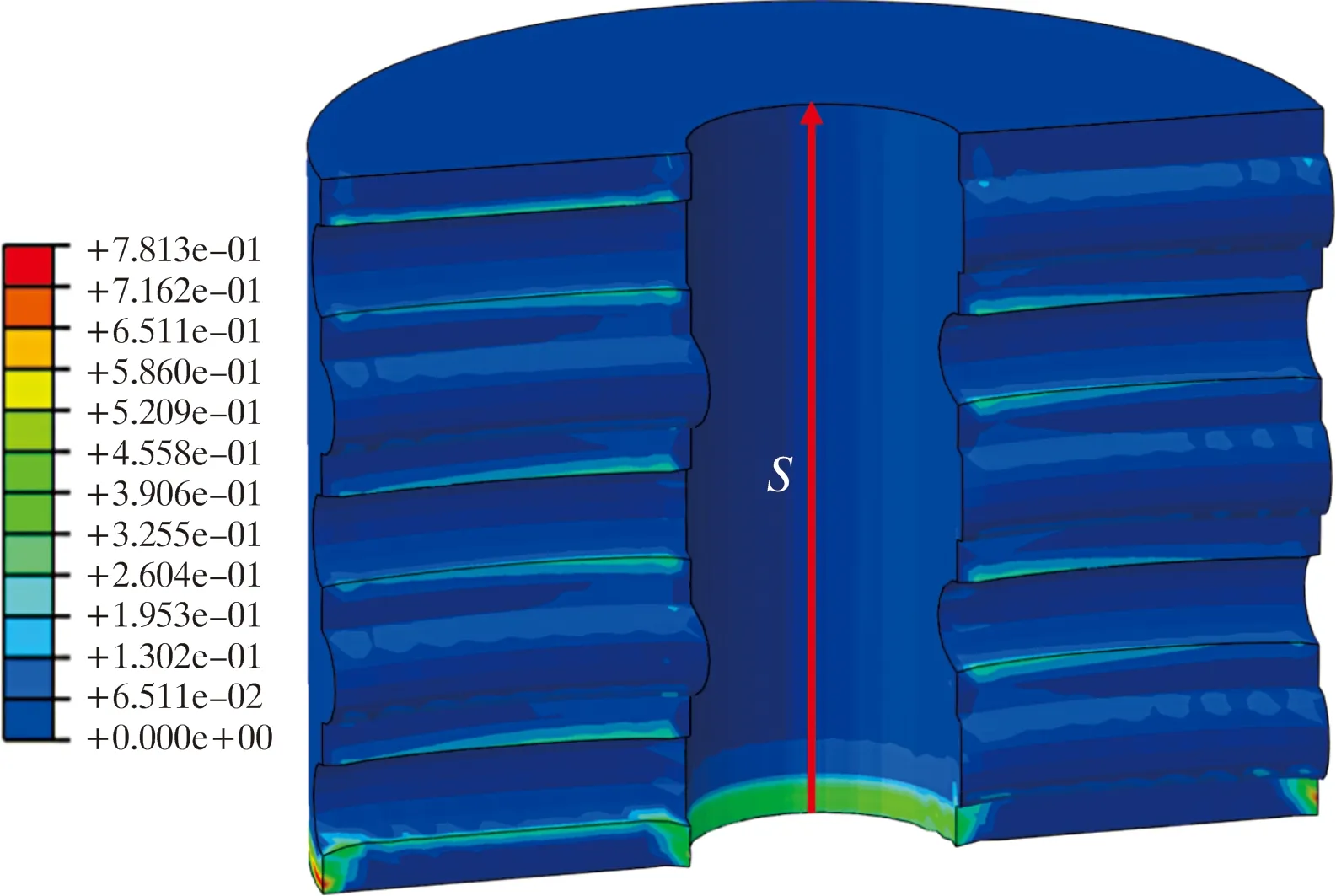
图7 连续管静止时胶筒应变能密度云图Fig.7 Cloud chart for strain energy density of stripper on coiled tubing static condition

由图7可知，胶筒与连续管接触密封面下端的应变能密度相对较大，但值较小。在胶筒与连续管接触面中心沿Y轴由下至上取路径S，连续管静止(ν=0)、起升和注入时路径S上应变能密度分布如图8所示。

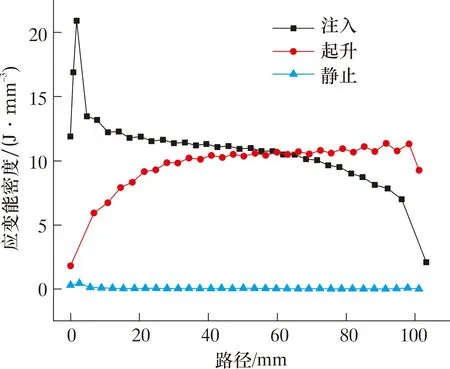
图8 路径S上应变能密度分布曲线Fig.8 Strain energy density distribution on path S

依据裂纹萌生理论，应变能越大表示橡胶的疲劳寿命越短，可靠性越低[31]。当连续管处于上下运动状态时，胶筒上下两端接触面上应变能密度较大。这一现象会导致胶筒上下两端接触面萌生裂纹，发生疲劳，出现撕裂、掉胶等现象，与第1节中现场胶筒的失效现象吻合，验证了有限元分析模型的可靠性。

2.3.2 摩擦力影响因素分析

(1)连续管运动方向和速度。

文献[4]研究表明，连续管的起升和注入影响胶筒与连续管间的接触应力分布，因此有必要开展连续管的运动对胶筒摩擦力的影响研究。假设连续管与胶筒之间的摩擦因数为0.1，计算连续管运动速度v分别为-600、-256、-100、0、256、600 mm/s时的连续管摩擦力，结果如图9所示。由图9可知，起升时连续管的摩擦力比注入时大，运动方向一致时，运动速度大小对连续管的摩擦力几乎无影响。

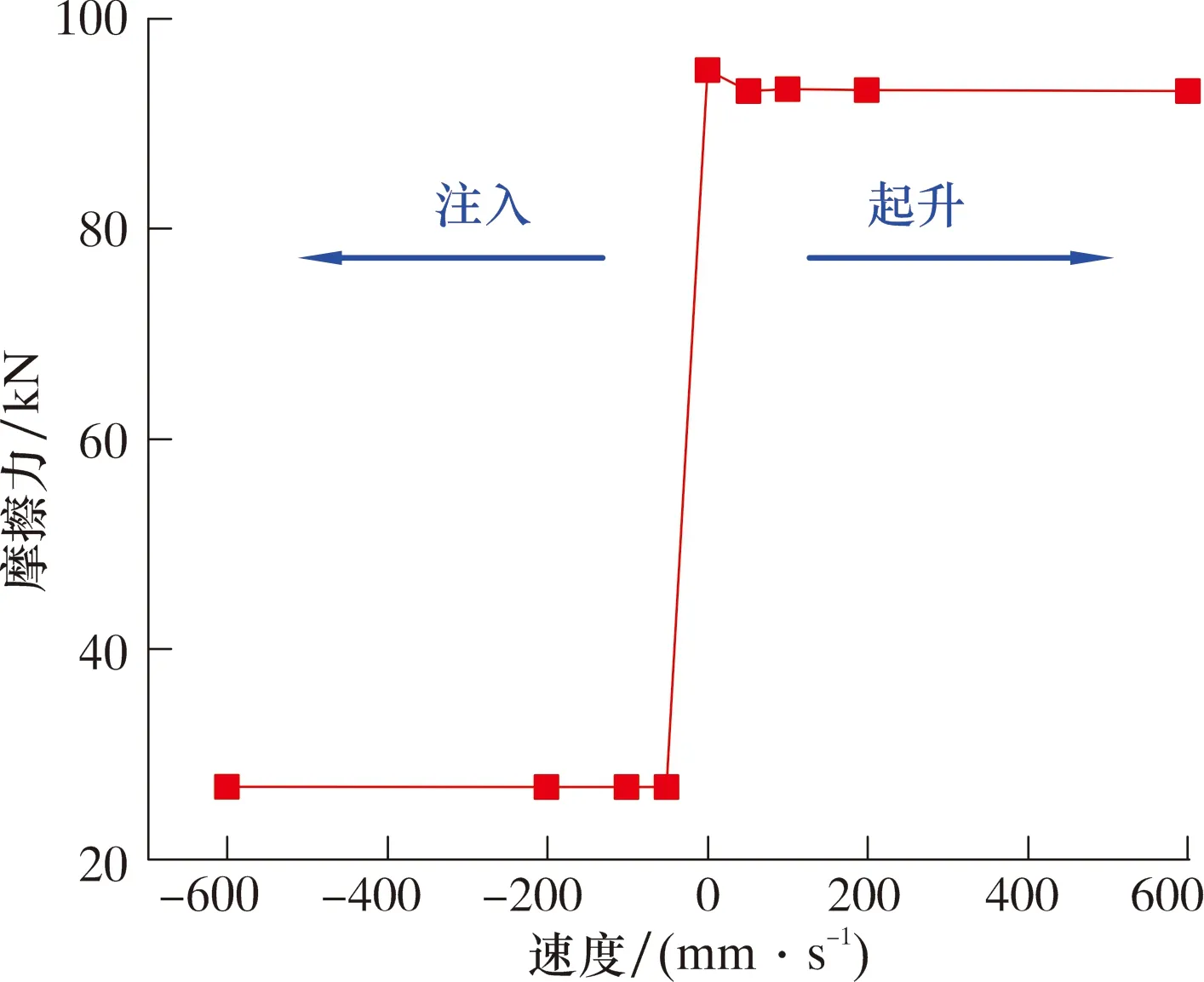
图9 运动速度和方向对连续管的摩擦力影响Fig.9 Influence of movement velocity and direction on the friction of coiled tubing

(2)摩擦因数。

为了研究胶筒与连续管的摩擦因数对连续管过防喷盒摩擦力的影响，计算当井筒介质压力为70 MPa，连续管与胶筒之间摩擦因数分别为0.01、0.05、0.10、0.20、0.30和0.40，连续管起升(v=256 mm/s)和注入(v=-256 mm/s)时的胶筒摩擦力，结果如图10所示。

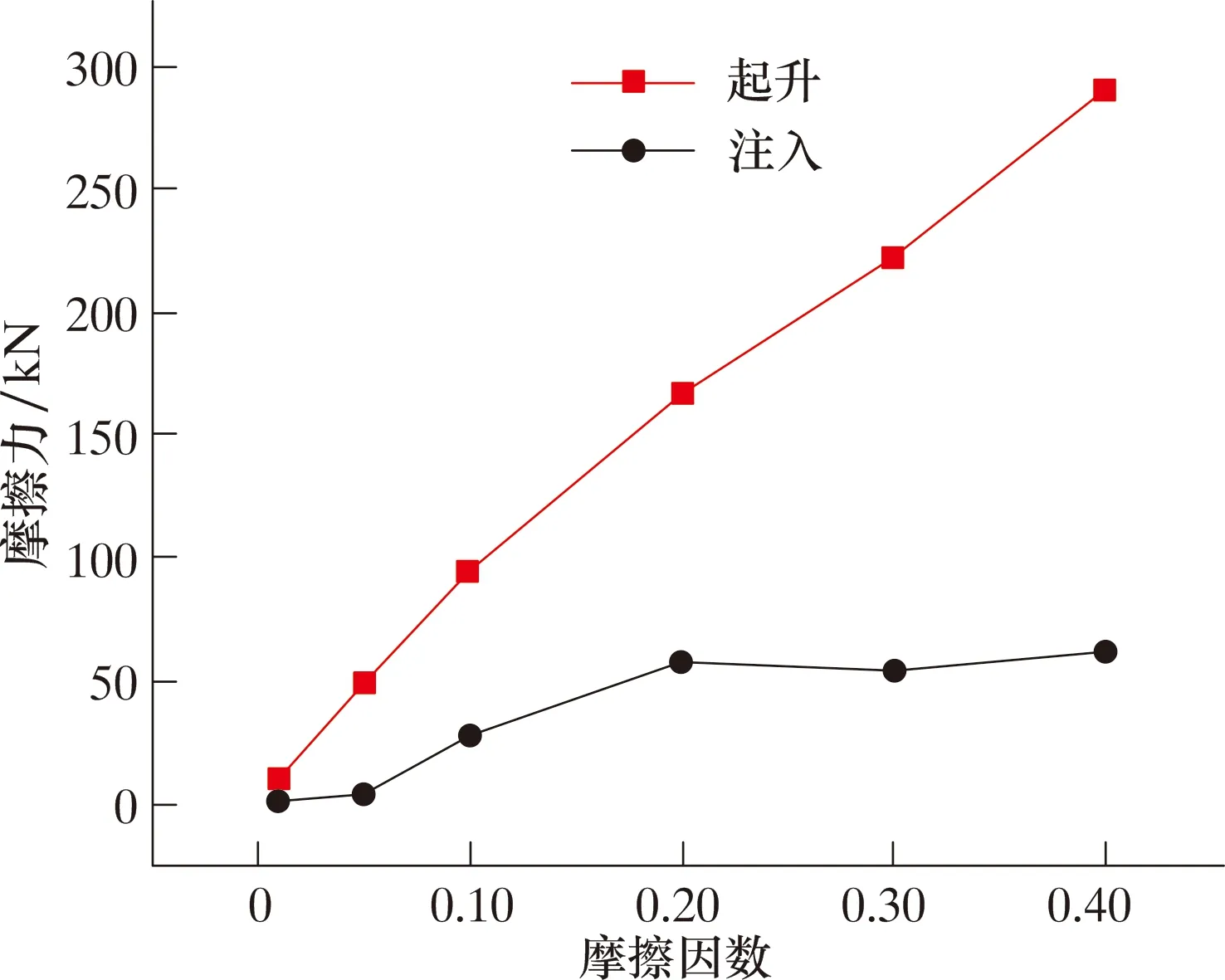
图10 摩擦因数对连续管摩擦力的影响曲线Fig.10 Influence of friction factor on the friction of coiled tubing

由图10可知：随着摩擦因数增大，起升连续管时胶筒的摩擦力增加；注入连续管时胶筒的摩擦力先随摩擦因数增加而增加，当摩擦因数达到0.20以后，摩擦力几乎保持不变。此外，起升连续管时胶筒的摩擦力大于注入时，且随着摩擦因数增大，差值越来越大。

(3)井内介质压力。

为了研究井筒介质压力pw对胶筒密封能力及连续管过防喷盒摩擦力的影响，计算当连续管与胶筒的摩擦因数为0.10，井筒介质压力分别为10、30、50和70 MPa，连续管起升和注入时的胶筒摩擦力，结果如图11所示。由图11可知：随着井筒介质压力增大，胶筒的摩擦力逐渐增大；起升连续管时胶筒的摩擦力大于注入时，且随着井内介质压力增加，差值越来越大。这一现象与实际应用一致，进一步证明了有限元分析的可靠性。

图11 井筒介质压力对胶筒摩擦力影响曲线Fig.11 Influence of wellbore medium pressure on the friction of stripper

3 连续管稳定性分析

依据注入头的结构可知，注入时连续管离开注入头夹持块至防喷盒导入口时处于径向无支撑状态，如图12所示。

假设连续管的稳定性分析符合压杆稳定理论，无支撑段的连续管可简化为两端铰支压杆[8]，不失稳的临界压力如下式所示：

(3)

式中：I为连续管惯性矩，m4；E为连续管弹性模量，MPa，L为无支撑段连续管的长度，m；μ为长度因子，无量纲。

连续管注入井内时，由上顶力引起的连续管轴向压力Fmax最大，即有：

(4)

式中：p0为井口压力，MPa；D为连续管外径，mm。

注入头将连续管注入井内需克服的最大力为FT=Fmax+Ff。

在注入井筒前，连续管需先经过滚筒和导向器后再进入注入头，共经历 3 次曲率变化。虽然在材料自身作用下产生弹性回复，但仍存在一定的残余曲率，会降低连续管失稳的临界压力[8]。因此，为了保证连续管不发生失稳，在设计连续管无支撑段长度值时，应考虑安全系数，取安全系数值为4[8]，即有：

(5)

为了得到连续管与胶筒间摩擦因数对连续管无支撑段最大允许长度的影响规律，计算当井筒介质压力为10、30、50和70 MPa，连续管与胶筒的摩擦因数分别为0.05、0.10、0.20、0.30和0.40时，对应的无支撑段最大允许长度，结果如图13所示。由图13可知：同一摩擦因数下，随着井筒介质压力增大，连续管无支撑段的最大允许长度减小；当井筒介质压力为10和30 MPa时，随着摩擦因数增大，无支撑段的最大允许长度值减小；当井筒介质压力为50 MPa时，摩擦因数在0.05～0.30之间，随着摩擦因数增大，无支撑段的最大允许长度值减小；摩擦因数在0.30～0.40之间，无支撑段的最大允许长度值变化较小，约为0.50 m。当井筒介质压力为70 MPa时，摩擦因数在0.05～0.20之间，随着摩擦因数增大，无支撑段的最大允许长度值减小；摩擦因数在0.20～0.40之间，无支撑段的最大允许长度值变化较小，约为0.46 m。

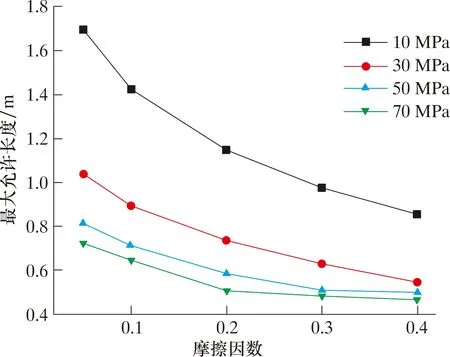
图13 不同压力和摩擦因数时无支撑段最大允许长度分布Fig.13 Maximum allowable length distribution of unsupported section under different pressures and friction factors

4 结 论

(1)连续管防喷盒胶筒的主要磨损形式为磨粒磨损；连续管过防喷盒的摩擦力是连续管表面粗糙微凸体对胶筒密封表面的压缩与切削产生的机械作用力。

(2)连续管与胶筒之间的摩擦因数越大，连续管起升时摩擦力越大。井筒介质压力为70 MPa时，连续管注入时的摩擦力先增加，但随后几乎保持不变。

(3)井筒介质压力、胶筒摩擦因数越大，连续管初入井内时失稳的可能性越大，连续管无支撑段最大允许长度值越小。考虑到作业过程中摩擦因数的变化和连续管的残余曲率，ø38.1 mm的连续管无支撑段长度值应小于0.46 m。