基于ABAQUS的分层注水封隔器胶筒有限元分析

陈 瑞，王晓虎

（海洋石油工程股份有限公司，天津 300451）

采油分层注水工艺中，在轴向载荷作用下，具有弹性并起到密封作用的封隔器重要元件——胶筒将承受轴向压缩和径向膨胀作用，此时胶筒填满管套环空，通过与套管内壁相互的接触压力实现其功能，达到阻断井液及压力和封隔上下分注层的作用。在注水过程中，胶筒与套管之间产生的相互作用将严重影响注水管柱系统的受力状况[1-4]。

研究封隔器胶筒的力学行为，尤其是对胶筒与套管间摩擦力随轴向压力的动态变化过程进行研究，对注水管柱力学分析、准确确定封隔器在井下的位置以及分层注水的成功与否具有重大的意义，并且为整体研究注水管柱受力变形提供了一定的理论依据[5-7]。

1 理论基础

在分层注水过程中，封隔器胶筒系统工作时存在许多相互接触运动的部分，包括胶筒与隔环、胶筒与套管、胶筒与中心管等，而这本身就是一种非常复杂的接触问题。接触原理是处理该问题的基础理论依据，也是封隔器胶筒系统进行有限元分析的理论基础[8]。

对于典型超弹性橡胶材料的胶筒，通常用不可压缩橡胶材料Mooney-Rvilin模型来描述其参数变化关系，并有如下的假设：

（1）橡胶本身具有不可压缩的性质，并且在未发生变形时为各向同性的材料；

（2）在承受剪切应力时，可以先承受拉伸作用，然后在平面上施加剪切作用力，整体上满足胡克定律作用。

封隔器胶筒所采用的丁腈橡胶材料可以通过应变能密度函数U来表达。

式中，I1，I2和I3分别为第一、二、三变形张量；1λ，2λ和 3λ分别为3个主方向的伸缩比。

在短暂时间变化内和较为稳态的温度状况下，橡胶往往被描述为各向同性且不可压缩的材料，并且

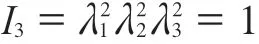
U的级数形式表示为

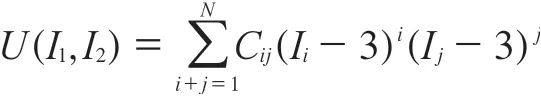
式中，Cij为力学性能常数。

在弹性体非线性有限元分析中，通过推导，可以得出Mooney-Rvilin模型：

式中，C1和C2为力学性能常数。

2 仿真分析

2.1 模型简化

压缩式封隔器由许多零部件装配而成，在其注水过程中主要涉及到的部件有胶筒以及与胶筒产生摩擦接触的中心管、隔环和套管元件，本工作在建模中对上述零部件予以考虑。由于胶筒、中心管、隔环和套管同样为轴对称零件，并且整个胶筒系统承受的坐封压力也是轴对称的，因此为了降低仿真计算量，可以使用轴对称模型，并且通过设置更为精细的网格，提升计算精度。

在分层注水过程中，封隔器附近套管和中心管柱相当于上下两端固定，套管外侧一般由固井水泥固定，因此套管外侧固定，上下隔环固定一侧，另外一侧施加载荷压力（上方施加坐封力）。最上面的隔环给胶筒施加轴向力，使胶筒出现轴向的压缩变形和径向膨胀作用，且跟注水管柱和套管内壁贴紧，起到密封注水管柱和套管环形空间的作用。因此，确定模型边界条件：套管外侧水平X方向固定，中心管和套管上下端竖直Y方向固定，最下端隔环自由度完全约束，并且对最上端隔环施加相应载荷，以模拟实际注水过程中注入液所产生的压力效果。

封隔器胶筒模型简化、载荷施加及网格划分如图1所示，封隔器胶筒有限元模型的几何参数如表1所示。

图1 封隔器胶筒模型简化、载荷施加及网格划分

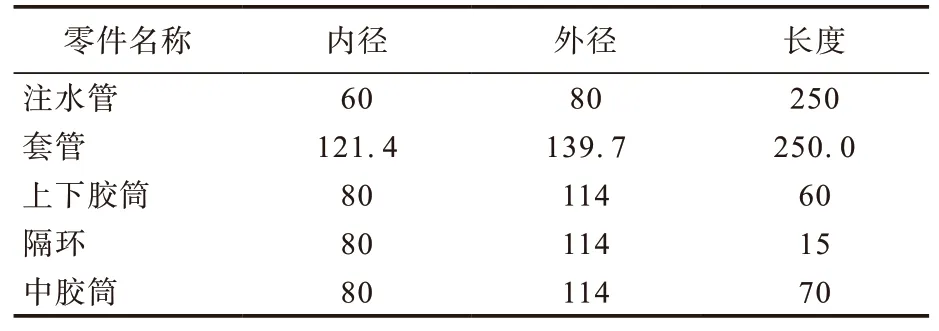
表1 封隔器胶筒有限元模型的几何参数 mm

根据Mooney-Rvilin模型所需参数设定指标，其中，上下胶筒国际橡胶硬度为85度，中胶筒国际橡胶硬度为90度。套管、注水管柱和隔环均按照小变形的碳钢或合金钢弹塑性参数选择。胶筒和套管内壁间的摩擦因数选为0.8；根据经验，胶筒自身相互接触及其与隔环的摩擦因数设为0.3；注水管与隔环的摩擦作用相对较小，摩擦因数设为0.1[9-10]。

2.2 数值模拟分析

针对不同需求的地层，需要通过调节配水嘴来调节注水量对其进行分层注水。此过程中，不同的注水压力会对注水管柱中起密封作用的封隔器产生较大影响。

正常作业中，坐封过程中Y341封隔器的压力为17 MPa，在注水管内憋压后，不断注入的配注液流过相连结构来压缩胶筒，进而导致其出现轴向压缩变形和径向膨胀变形作用，强烈挤压套管内壁，形成管柱上下层密封。

为了分析注水过程和封隔器胶筒的工作状况，有必要对胶筒压缩距、胶筒与套管间摩擦力及胶筒与套管间接触压力等随轴向压力改变的具体情况进行分析。

分别在注水压力P为5，8，11，14，17和20 MPa状态下，分析胶筒的工作状况，结果如图2所示。

2.2.1 胶筒长度变化

根据图2，可以获知胶筒轴向载荷与轴向变形之间的关系，如图3所示。

图2 胶筒变形云图

图3 胶筒轴向变形与轴向载荷的关系

随着轴向压力的增大，中胶筒首先与套管内壁发生接触，接着是加载端（上胶筒），然后才是非加载段胶筒（下胶筒）。出现这种现象是因为中胶筒较上下胶筒柔软，弹性模量也比较小，更容易被挤压膨胀变形，因此中胶筒最早与套管内壁发生接触；在压力逐渐施加过程中，中胶筒与外套管相互接触以后，两者之间的摩擦和相互挤压会导致下胶筒承受的轴向压力与变形均较小，因此上胶筒先于下胶筒与套管发生接触。

随着轴向压力的增大，胶筒压缩距离也逐渐增大，最初胶筒受压时压缩距离变化较为显著，随着压力继续增大，胶筒与套管内壁互相接触，胶筒被压扁并逐渐被压实，胶筒压缩距离变化趋势变缓。

2.2.2 摩擦力分析

根据模拟仿真结果，可以得到上、中、下胶筒和套管相互间摩擦应力的变化，并线性拟合出胶筒与套管间摩擦应力曲线，如图4所示。

由图4可知，随着轴向载荷的增大，胶筒与套管内壁间的摩擦应力也逐渐增大，并且总体呈线性关系，增大过程中胶筒摩擦应力大小略有波动，与胶筒橡胶材料的特性相符；当轴向载荷达到20 MPa时，胶筒与套管内壁间的摩擦应力可达9.8 MPa。

图4 胶筒与套管间摩擦应力曲线

2.2.3 Mises应力分析

由ABAQUS分析得出胶筒Mises应力云图如图5所示。

对图5进行分析可以得出以下结论。

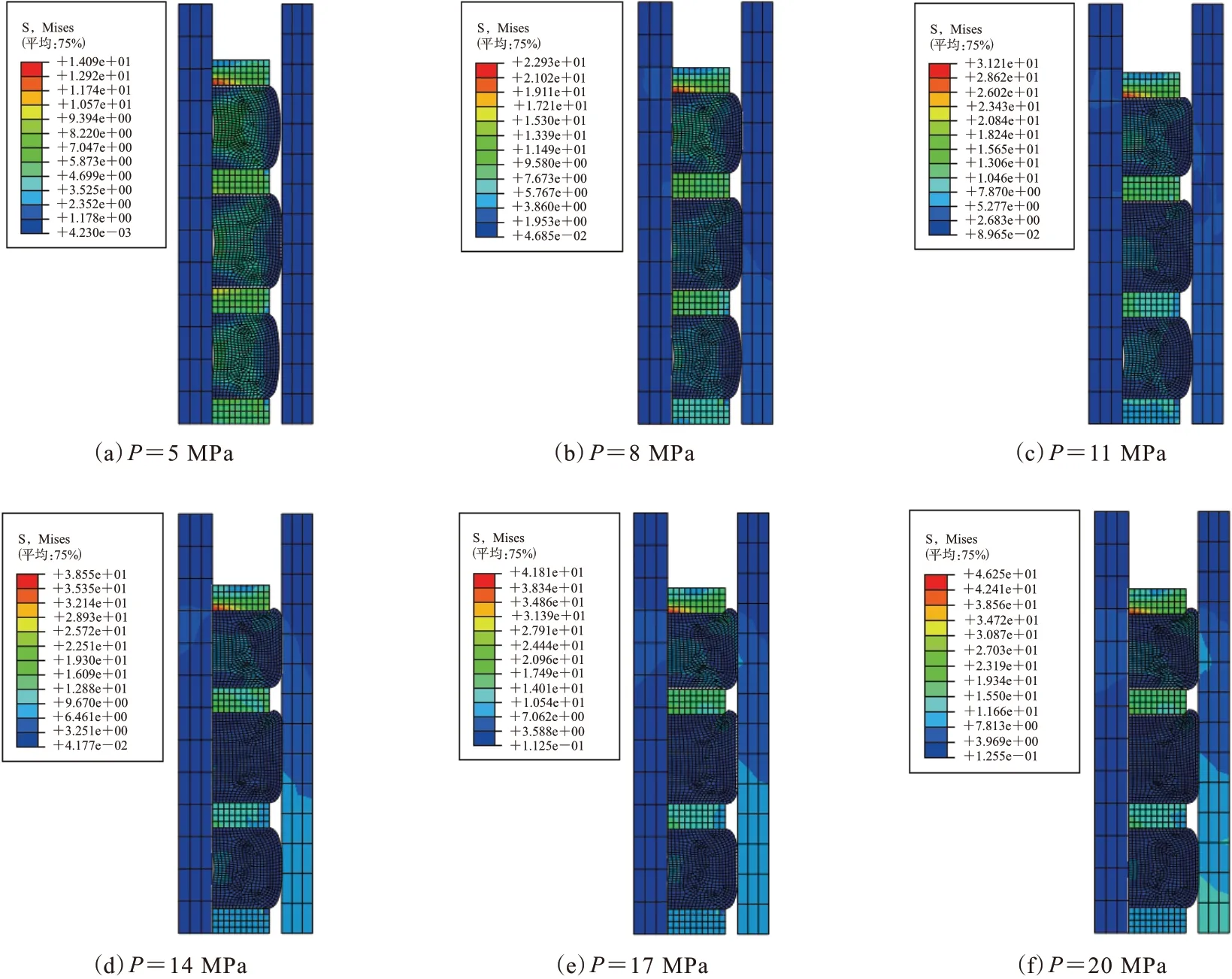
图5 胶筒Mises应力云图

（1）胶筒和套管内壁发生接触后，坐封压力逐渐增大，胶筒和套管内壁的接触长度相应增大，胶筒径向膨胀变化因为套管壁阻碍，胶筒内外表面同时向外产生鼓胀变化，并最终与套管牢牢紧密接触。可以看出，当轴向载荷超过11 MPa后，胶筒隔环处开始产生“突出”，随着载荷的增大“突出”更加明显，并且施加载荷端的上胶筒隔环处“突出”最明显，中胶筒次之。

（2）当轴向载荷逐渐增大时，胶筒系统所承受的应力也逐渐增大，并且最大应力集中在上胶筒上部（施载处）的隔环位置。

2.2.4 接触应力分析

分别对封隔器施加不同轴向载荷，根据有限元仿真分析结果，可以获得胶筒与套管间的接触应力云图，通过数据提取，将其沿从上到下的路径绘制出应力分布图（见图6），并分别绘制载荷施加过程中3个胶筒的最大接触应力变化状况（见图7），进行对比分析。

图6 不同注水压力下胶筒接触应力分布

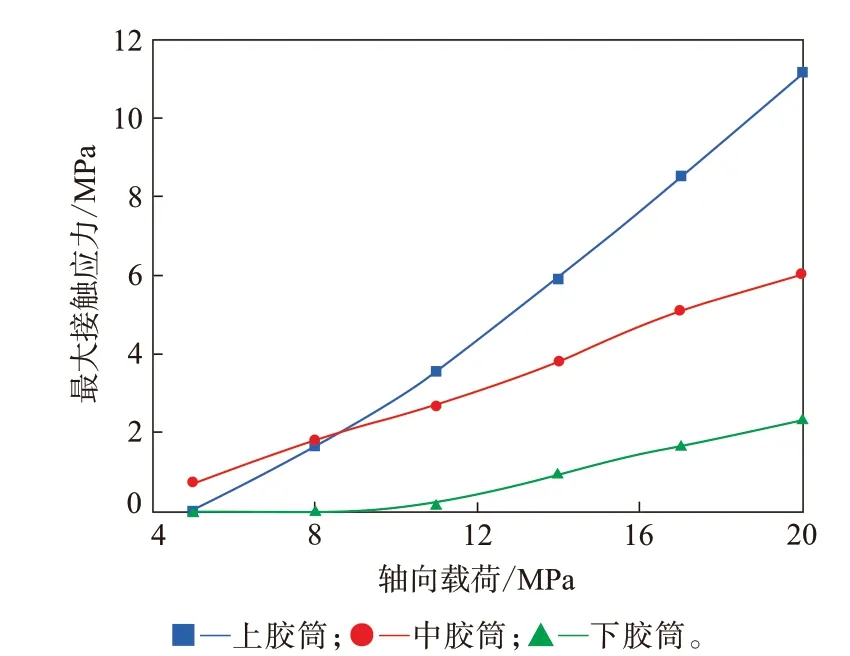
图7 上中下胶筒最大接触应力变化

从图6和7可以得知：封隔器3个胶筒的接触应力变化较大，并且分布也很不均匀；当载荷施加比较小时，3个胶筒中，中胶筒的接触应力相对而言最大，上下两个胶筒的接触应力较小；当载荷逐渐增大时，3个胶筒的接触应力也随之增大，并且胶筒逐渐被挤向载荷施加方向，中胶筒和下胶筒的增长趋势较为接近，而上胶筒变化趋势更为剧烈；在这个过程中，上胶筒的接触应力逐渐大于中胶筒的接触应力，第1个被压实，并且所承受的载荷最大。

3 结论

利用有限元仿真法对分层注水过程中封隔器胶筒力学及变形状况进行研究，得出下述结论。

（1）随着轴向压力的施加，中胶筒首先与套管内壁发生接触，接着是上胶筒，然后才是下胶筒，胶筒被压扁并逐渐被压实，胶筒压缩距离变化趋势变缓，最大应力集中在上胶筒上部隔环位置。

（2）胶筒与套管之间的摩擦应力变化与胶筒橡胶材料的特性相符，当轴向压力达到20 MPa时，胶筒与套管内壁间的摩擦应力可达9.8 MPa。

（3）封隔器3个胶筒的接触应力变化较大，并且分布也很不均匀。当载荷施加比较小时，3个胶筒中，中胶筒的接触应力相对最大，上下两个胶筒的接触应力比较小。当载荷逐渐加大时，上胶筒的接触应力逐渐大于中胶筒，第1个被压实，并且所承受的载荷最大。