井下暂堵可取封隔器密封结构设计与评价

卢 明, 廖华林, 武琳娜, 梁智飞, 刘 凯

(1中国石油大学·华东 2中石油西部钻探钻井工程技术研究院 3中石油煤层气有限责任公司)

暂堵可取封隔器较好地解决了坐封、打捞、解封操作复杂、成功率低的难题，能够实现单趟压裂多个层段，是改善薄差油层的有效技术[1-7]。但由于井下工况复杂，多次坐解封管柱会产生自锁现象，在高温、高压且腐蚀性强的环境中多次压缩和回弹，会削弱封隔器密封性能[8-11]。本文设计了一种胶筒结构，并建立非线性有限元模型，以胶筒-套管间接触压力评价相应的密封性，对保障钻具安全、提高油田产量具有重要意义。

1 有效密封结构设计与分析

为满足单趟管柱贯穿多个层段的密封性需求，优化后的胶筒设计为三段式组合结构，如图1所示。其中，上、下胶筒几何尺寸、力学参数完全相同，邵氏硬度为90°；中部胶筒尺寸较短，且弹性模量较低，邵氏硬度为70°。不同胶筒之间设有金属隔环。

依照现场工序，胶筒受力可划分为初封和工作两个阶段[12]。若要满足工作阶段的条件，需要在初封阶段基础上继续施加载荷以保证胶筒和套管产生足够的接触压力。

图1 有效密封结构示意图

保证胶筒密封所需临界总压缩力F为：

F=F0+FΔp

(1)

式中:F0—临界初封力，N；FΔp—满足密封要求应继续施加的压缩力，N。

(2)

式中:r—胶筒曲率半径，mm；σz—轴向上的法向分量，Pa。

已知胶筒轴向相对变形，可按广义胡克定律分别求取径向、切向、轴向上的法向分量σr，σθ，σz：

(3)

(4)

(5)

式中：εr，εθ，εz—分别为胶筒径向、切向和轴向上的相对伸长量，mm；E—胶筒弹性模量，MPa；μ—胶筒橡胶材料泊松比。

(6)

(7)

式中:u—弹性物体径向位移，mm；R1—胶筒内径，mm；R2—胶筒外径，mm；R3—套管内径，mm。

(8)

将式(6)、式(7)、式(8)代入式(3)、式(4)、式(5)，得：

(9)

(10)

(11)

此时，

(12)

压差作用下胶筒受力的平衡条件为：

Δp·A1=f(p1S1+p2S2)

(13)

(14)

式中：Δp—工作时封隔器承所受压差，MPa；A1—套管与中心管外径间环形截面面积，mm2；f—胶筒和套管、套筒间的摩擦系数；p1、p2—分别为轴向载荷作用下，胶筒内、外壁上的压强，MPa；S1、S2—分别为压差作用下变形后，胶筒内、外密封面侧面面积，mm2。

为简便计算，取：

p1S1=p2S2

(15)

p1=p2=p

(16)

式中:p—压差下产生的接触压强，MPa。

S1=S2=2πR1h(1-ε)

(17)

(18)

在轴向载荷作用下，胶筒内、外密封表面上的径向压力和轴向压力可视为相等，即：

(19)

联立可得:

(20)

2 非线性有限元模型建立

在研究封隔器密封性的常见方法中[13-15]，室内试验成本较高，且结果受环境因素影响；理论计算步骤繁琐，且受假设条件限制；而数值模拟能以较低的成本、简洁的步骤合理分析非线性问题。由于胶筒所属的超弹性材料具有材料/几何双重非线性特征[16-17]，同时胶筒与套管、套筒间摩擦较大，因此胶筒密封性能分析相对复杂。本文考虑多种材料耦合接触问题，在Mooney-Revlin函数基础上[18-19]，建立了对应的非线性有限元模型。

结合胶筒几何形状、材料等围绕轴线均匀分布特征与结构复杂边界条件，本文将三维研究对象简化为二维平面对称模型，如图2所示。

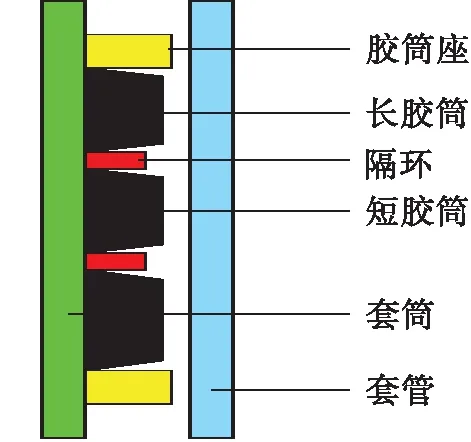
图2 胶筒机构结构模型

模型各部件的几何参数如表1所示。

表1 胶筒结构几何参数

Mooney-Revlin应变能密度函数为：

W=C10(I1-3)+C01(I2-3)

(21)

(22)

(23)

式中:W—应变能，J；C10、C01—力学常数,通过试验测定计算获取[20-21]；σi(i=1,2,3)—3个方向主应变。

在Mooney-Revlin函数中，胶筒弹性模量E和邵氏硬度Hr及C10、C01的关系为：

lgE=0.0198Hr-0.5432

(24)

E=6(C10+C01)

(25)

取C01∶C10=0.5，Hr=90(长胶筒)/70(短胶筒)，代入函数求得E，C10，C01。

另外，胶筒座、隔环、套筒和套管的材料为低碳钢或合金钢，E取206 GPa，泊松比μ取0.3。摩擦因数f取0.5。模型力学参数如表2所示。

表2 胶筒结构力学参数

采用罚单元法求解胶筒和套管、套筒之间的接触问题，划分密封胶筒结构模型网格。

3 两种阶段下密封性评价

假设钢材为刚性，并作为胶筒变形的约束边界。研究认为，工作过程中封隔器的承压能力与胶筒和套管壁间接触压力存在函数关系，只有在接触压力不小于工作压差时，才能保证密封效果[19-21]。因此，本文以接触压力为标准，对胶筒结构的密封性能展开评价。

3.1 初封阶段密封性评价

根据上述计算可知，本文中胶筒压缩到套管壁所需临界初封力F0=42 176 N。将下压座固定，通过有限元数值模拟可以得到暂堵可取封隔器密封结构中的三个胶筒在初封阶段的接触压力等值线云图。

将上、中、下胶筒和套管间接触压力作为因变量，所对应的胶筒沿套管壁轴向长度作为自变量，而三个胶筒和套管壁接触的上顶点分别为横坐标原点，绘制相应的接触压力随轴向长度的拟合变化曲线，如图3所示。

由图3可知，初封阶段，三部分胶筒和套管间接触压力都呈马鞍形，上端接触压力均大于下端接触压力。其中，中胶筒最软，且上端更接近载荷，因此最大接触压力出现在中胶筒轴向3.1 mm处，而最小接触压力出现在下胶筒轴向21.9 mm处。同时，中胶筒和隔环间的接触压力最大，上胶筒次之，下胶筒最小。而胶筒和套筒外壁间的接触压力始终很小。

图3 初封时胶筒和套管间接触压力变化曲线

观察拟合曲线发现，初封后上胶筒压缩量为36.2%；中胶筒压缩量为36.3%；下胶筒压缩量为35.9%。中胶筒施加载荷后首先变形并和套管壁接触，产生接触压力和摩擦力，使得上胶筒先于下胶筒被压缩。而上胶筒和套管壁接触后，产生更大的接触压力和摩擦力，使得下胶筒受到的轴向载荷相对较小，因此下胶筒变形量最小。

3.2 工作阶段密封性评价

初封过程中施加42 176 N的压力，胶筒压缩后封隔器自锁，认为初封载荷一直存在。假设暂堵可取封隔器的承压能力是60 MPa，安全系数S=1.2，则工作时封隔器所承受压差Δp为72 MPa。根据上述计算可知，本文FΔp为80 430 N。将下压座固定，从上压座上端面施加压力。通过有限元数值模拟得到封隔器密封结构中的三个胶筒在工作阶段的接触压力等值线云图。

同样将上、中、下胶筒和套管间接触压力作为因变量，胶筒轴向长度作为自变量，和套管壁接触的上顶点作为横坐标原点，绘制相应的拟合变化曲线，如图4所示。

图4 工作时胶筒和套管间接触压力变化曲线

由图4可知，在工作阶段，三胶筒和套管间接触压力呈马鞍形，上、中胶筒上端接触压力大于下端，下胶筒下端接触压力大于上端。最大接触压力出现在中胶筒轴向3.6 mm处；最小接触压力出现在下胶筒轴向26.7 mm处。而中胶筒和隔环间的接触压力最大，上胶筒次之，下胶筒最小。与初封阶段不同，胶筒和套筒外壁间的接触压力最大值出现在胶筒两端，中间部分接触压力很小。

观察拟合变化曲线发现，工作阶段上胶筒压缩量为36.8%；中胶筒压缩量为36.9%；下胶筒压缩量为36.1%。初封后施加工作载荷，上胶筒又被压缩0.6%；中胶筒又被压缩0.6%；下胶筒又被压缩0.11 mm，占总长度0.2%。最大接触压力值出现在中胶筒上端，且中胶筒和套管间的接触压力值均大于压差72 MPa，说明工作阶段暂堵可取封隔器主要依靠中胶筒实现密封；另外，上胶筒的大部分接触压力及下胶筒的小部分接触压力也大于72 MPa，说明上、下胶筒能够起到协助密封的作用。

4 结论

1)各胶筒和套管间接触压力始终呈马鞍形，胶筒-套管与胶筒-隔环的最大接触压力均位于中胶筒，最小接触压力均位于下胶筒。在初封阶段，各胶筒上端与套管间的接触压力均大于下端；而在工作阶段，上、中胶筒上端与套管间的接触压力大于下端，但下胶筒下端与套管间的接触压力大于上端。

2)初封后上胶筒长度被压缩36.2%，中胶筒长度被压缩36.3%，下胶筒被压缩35.9%。随后施加工作载荷，上胶筒又被压缩了总长度的0.6%，中胶筒又被压缩了总长度的0.6%，下胶筒又被压缩了总长度的0.2%。

3)最大接触压力值出现在中胶筒的上端，且中胶筒和套管间的接触压力值均大于压差，说明工作阶段暂堵可取封隔器主要依靠中胶筒实现密封。而上胶筒的大部分接触压力及下胶筒的小部分接触压力也大于压差，说明上、下胶筒能够起到协助密封的作用。