精细广义复合多元多尺度反向散布熵及其在滚动轴承故障诊断中的应用

郑近德 陈焱 童靳于 潘海洋

摘要：多尺度反向散布熵能够有效度量时间序列的复杂性，但在粗粒化构造上存在缺陷，且在表征滚动轴承非线性故障特征时缺乏对其他通道同步信息的有效利用。为了准确提取轴承信号的故障特征，结合精细化和广义复合多尺度的思想，将表征同步多通道数据多变量复杂度的多变量熵理论应用到轴承故障诊断中，提出了精细广义复合多元多尺度反向散布熵（RGCMvMRDE）。在此基础上，提出了一种基于RGCMvMRDE与引力搜索算法优化支持向量机（GSA-SVM）的滚动轴承故障诊断方法。首先，利用RGCMvMRDE全面表征滚动轴承故障特征信息，构建故障特征集；其次，采用GSA-SVM对故障类型进行智能识别；最后，将所提方法应用于滚动轴承实验数据分析，并将其与现有基于多尺度反向散布熵、广义多尺度反向散布熵和精细复合多元多尺度排列熵的故障特征提取方法进行了对比。研究结果表明，所提RGCMvMRDE不仅能够有效和精准地诊断轴承的不同故障类型和故障程度，且诊断效果优于上述对比方法。

关键词：精细广义复合多元多尺度反向散布熵；滚动轴承；故障诊断；特征提取

中图分类号：TH165.3

DOI：10.3969/j.issn.1004132X.2023.11.007

RGCMvMRDE and Its Applications in Rolling Bearing Fault Diagnosis

ZHENG Jinde CHEN Yan TONG Jinyu PAN Haiyang

School of Mechanical Engineering，Anhui University of Technology，Maanshan，Anhui，243032

Abstract： Multi-scale reverse dispersion entropy（MRDE） might effectively measure the complexity of time series， but MRDE had defects in coarse-grained structure and lacked the effective use of other channel information in characterizing the nonlinear fault characteristics of rolling bearings. To accurately extract fault features from bearing signals， combined with the ideas of refinement and generalized composite multi-scale， the multi-variate sample entropy theory that characterized the multi-variate complexity of synchronized multi-channel data was applied to the rolling bearing fault diagnosis and RGCMvMRDE was proposed. Then， a rolling bearing fault diagnosis method was proposed based on RGCMvMRDE and gravitational search algorithm support vector machine（GSA-SVM）. Firstly， the RGCMvMRDE was applied to comprehensively characterize the fault feature information of rolling bearings and the fault feature sets were contracted. Secondly， GSA-SVM was used to identify the fault type intelligently. Finally， the proposed fault diagnosis method was applied to analyze experimental data of rolling bearing with comparing with the existing fault feature extraction methods based on MRDE， generalized MRDE（GMRDE） and refined composite multi-yariate multi-scale permutation entropy RCMvMPE. The results indicate that the proposed method may effectively and accurately identify different fault types and fault degrees of rolling bearings and the diagnosis effectiveness is better than those of the compared methods.

Key words： refined generalized composite multi-variate multi-scale reverse dispersion entropy（RGCMvMRDE）; rolling bearing; fault diagnosis; feature extraction

0 引言

作為旋转机械中应用广泛的关键部件，滚动轴承的运行状态关乎整台机器的性能以及整条生产线的安全，一旦发生故障，轻则引发机械产品加工的质量问题，重则造成严重伤亡和财产损失，因此，对滚动轴承早期故障进行及时诊断有着积极的理论和现实意义［1-2］。

由于摩擦、阻尼、刚度、耦合等因素影响，滚动轴承振动信号中潜藏的故障成分异常复杂［3-4］。滚动轴承故障诊断的核心在于高质量特征的获取，对于基于熵理论的特征提取方法，如近似熵［5-6］、模糊熵［7-8］、排列熵［9-10］（permutation entropy， PE）和散布熵［11-12］（dispersion entropy， DE）等，因其强大的非线性数据处理性能而被相关学者应用于旋转机械的故障诊断领域。如PE通过统计相空间内各向量的排列规律，能够有效表征系统的复杂性程度，且该算法具有理论简单、处理速度快等优点，故得到广泛应用。但PE只考虑了幅值顺序而忽略了大小信息，为克服这一缺陷，LI等［13］在PE基础上提出反向散布熵（reverse dispersion entropy， RDE），同时引入散布熵的幅值信息和反向排列熵的距离信息，所提RDE兼具两者的优势。但是RDE仅能提取时间序列单一尺度上的信息，易造成其他尺度上信息的遗漏，为此，相关学者将多尺度分析［14］和RDE结合，提出了多尺度反向散布熵［15］（multi-scale reverse dispersion entropy， MRDE）。

MRDE考虑多个尺度因子下时间序列携带的信息，有效弥补了RDE单一尺度分析的不足，但将MRDE应用于故障特征提取中仍存在以下缺陷：①MRDE粗粒化序列构造过程中的均值处理方式会减缓原始信号的突变行为，不可避免地造成部分信息的严重缺失，影响特征提取的效果［16］；②MRDE中新粗粒化序列的长度等于原时间序列长度与尺度因子的比值，造成多尺度计算受原始数据长度等因素影响，干扰最终诊断的效果［17］；③MRDE只利用单一通道的振动数据实现滚动轴承的局部故障诊断，而滚动轴承工作时振动传递路径复杂，综合利用多个通道故障信息才能实现滚动轴承更全面的故障诊断［18］。

针对上述的不足，本文受精细化和广义思想的启发［19-20］，将粗粒化过程中的一阶矩推广到二阶矩，并结合精细化处理方式有效减少基于粗粒化定义的多尺度计算过程中信息的丢失，最后基于多维嵌入重构理论将MRDE拓展到多变量。由此提出一种精细广义复合多元多尺度反向散布熵（refined generalized composite multi-variate multi-scale reverse dispersion entropy， RGCMv-MRDE）新算法，以实现深层故障特征信息的全面提取。基于此，考虑将RGCMvMRDE应用于滚动轴承故障特征的提取，结合引力搜索算法优化支持向量机［21-22］（gravitational search algorithm support vector machine， GSA-SVM），提出了一种基于RGCMvMRDE和GSA-SVM的滚动轴承故障诊断新方法。首先利用RGCMvMRDE全面表征滚动轴承故障特征信息，构建故障特征集；然后采用基于GSA-SVM建立的多故障分类器进行训练，利用已训练完成的分类器对故障类型进行智能识别［23］；最后，将所提方法应用于滚动轴承实验数据分析，并与对比方法进行了诊断效果的比较。

1 精细广义复合多元多尺度反向散布熵

1.1 多尺度反向散布熵算法

反向散布熵（RDE）通过引入散布熵的幅值信息和反向排列熵的距离信息，显著提高了特征提取的稳定性。多尺度反向散布熵（MRDE）能从多个尺度全面表征时间序列的复杂性，计算步骤概述如下：

（2）计算不同尺度因子τ下粗粒化序列的反向散布熵值（即多尺度反向散布熵）：

EMRDE（x，c，m，λ，τ）=ERDE（y（τ），c，m，λ）（2）

其中，EMRDE为多尺度反向散布熵值；ERDE为反向散布熵值；参数c、m、λ分别为类别数、嵌入维数和时延。显然，当τ=1时，MRDE为单尺度RDE。RDE的详细计算过程参见文献［13］。

1.2 精细广义复合多元多尺度反向散布熵算法

MRDE进行粗粒化序列构造时，采用数据均值的特征得到原始数据不同尺度下的时间序列信息，但在故障信号特征提取过程中，均值处理的方式会不可避免地導致原始信号的动力学突变行为被弱化。为了时间序列的动态变化得到精确阐述，本文考虑采用二阶矩（即方差）代替传统粗粒化方法中使用的一阶矩（即均值），提出广义多尺度反向散布熵（generalized multi-scale reverse dispersion entropy， GMRDE）。即在MRDE计算步骤（1）中，对于尺度因子τ，只计算τ≥2时原序列的方差得到新的广义序列，然后计算不同尺度因子τ下广义序列的RDE值，并将其作为原始序列在该尺度因子下的GMRDE值。GMRDE将粗粒化过程中的均值计算推广至二阶矩，理论上优于MRDE方法，但仍存在一定缺陷，多尺度化过程需对数据先进行等距分割再求方差，这种处理方式计算过程简单、速度快，但熵值的稳定性受数据长度等因素影响，且忽略了由其他初始位置进行处理的时间序列中潜藏的信息。

针对上述问题，采用精细化处理方式［24］，先计算每个粗粒化序列散布模式的概率，再求这些概率的均值。基于此，所定义的精细广义复合多元多尺度反向散布熵（RGCMvMRDE）方法的计算步骤如下：

（1）考虑多元信号x=［xk，i］（k=1，2，…，P;i=1，2，…，N），记为P×N的矩阵，采用下式定义广义粗粒化序列：

其中，P为信号通道的数量；N为多通道信号中每一通道信号的长度（即数据长度）；y（τ）k，l，j为在尺度因子τ下，k通道数据中第l（l=2，3，…，τ）个粗粒化序列的第j（j=1，2，…，N/τ）个值；x-k，i为xk，i的平均值。

（2）针对不同尺度因子τ，计算多通道数据下所有广义序列散布模式的概率，该概率等于嵌入向量映射到散布模式中的个数与嵌入向量元素个数的比值。值得注意的是：不同于单通道下粗粒化序列被重构为矩阵，多通道序列重构后表现为元胞形式，其散布模式概率的计算需首先分解为矩阵再考虑后续计算。

（3）计算τ个符号序列概率的均值，根据香农熵的定义，RGCMvMRDE值定义如下：

1.3 引力搜索算法优化支持向量机

支持向量机（support vector machine，SVM）是常用的按监督学习方式对数据进行二元分类的广义线性分类器。针对SVM的算法性能易受惩罚因子C和核函数参数g影响的问题，采用引力搜索算法（gravitational search algorithm， GSA）对其核函数参数进行优化。GSA是由RASHEDI等［25］基于牛顿万有引力定律基本思想提出的一种新型优化算法，利用群体中各物体之间的万有引力相互作用来实现优化信息共享。文献［25］研究结果表明，相较于一些现有的智能优化算法，GSA算法的全局搜索能力更优，且结构简单、易于实现。原始GSA算法具体的过程如下：

假设存在一个n维搜索空间，由L个粒子组成种群，则第i（i=1，2，…，L）个粒子的位置可表示为

Xi=（x（1）i，x（2）i，…，x（d）i，…，x（n）i）（5）

式中，x（d）i为第i个粒子在维度d上的位置。

首先，初始化粒子位置。在d维上t时刻下，粒子i与粒子j之间的引力大小被定义为

式中，Mpi（t）、Maj（t）分别为受力粒子i和施力粒子j的惯性质量；ε为常量；G（t）为随t变化的引力常数；Rij（t）为粒子i和粒子j两者的欧氏距离。

其次，适应度值的大小影响粒子的惯性质量Mi（t），适应度值越大，表示越接近所求的最优解。GSA算法中，根据下式更新粒子的惯性质量：

式中，Vfit，i（t）为粒子i在t时刻的适应度值；Vbest（t）、Vworst（t）分别为所有粒子中最好和最差的适应度值。

每一次迭代过程，粒子的速度和位置均按照牛顿第二定律进行更新，可表示为

其中，Vrand，i表示在［0，1］范围内的一个随机值；a（d）i（t）为粒子i在第d维上t时刻下的加速度; F（d）i（t）为粒子i在d维上受到的合力。GSA优化SVM的具体流程如图1所示。

2 基于RGCMvMRDE的滚动轴承故障诊断方法

2.1 仿真实验

在RGCMvMRDE的计算中，有4个参数值需要考虑和设定，包括时间序列长度（即数据点个数）N、类别数c、嵌入维数m和时延λ。文献［13］对RDE参数进行了讨论，认为m取值不宜过大，一般取2或3即可，c取4～8，λ取1，N＞cm。本文RGCMvMRDE中RDE参数与文献［13］中保持一致，选取m=3、c=4、λ=1。

蓝噪声（blue noise， bn）和紫噪声（violet noise， vn）是经过白噪声频谱处理得到的两种有色随机噪声，两者的波形及频谱如图2所示，可以看出，两者的时域波形相似，均较为随机和复杂，根据波形图难以直接区分两种噪声类型。取数据点个数N分别为2048、3076、4096、5120的蓝噪声和紫噪声作为研究对象，研究数据长度对RGCMvMRDE算法的影响，并与GMRDE算法、MRDE算法进行对比，分析结果如图3所示，其中，三种算法的参数设置一致。

由图3可知：①对于不同数据长度N下的蓝噪声和紫噪声，两者的RGCMvMRDE熵值均值曲线较为接近，且两种噪声的区分也非常明显，这说明数据长度对算法的影响较小，故本文设置N=2048；②对比图3a～图3c可以发现，在同一数据长度N下，RGCMvMRDE的熵值标准差更小，且熵值均值曲线更加平缓，表明采用精细复合处理提取的熵值特征更加稳定；③与图3a的MRDE相比，图3b的GMRDE和图3c的RGCMvMRDE提取的两种噪声均值曲线在大部分尺度上未出现熵值交叉的情况，能够更好地区分噪声类型，验证了本文所提方法采用广义粗粒化方式的优越性。

2.2 故障诊断模型

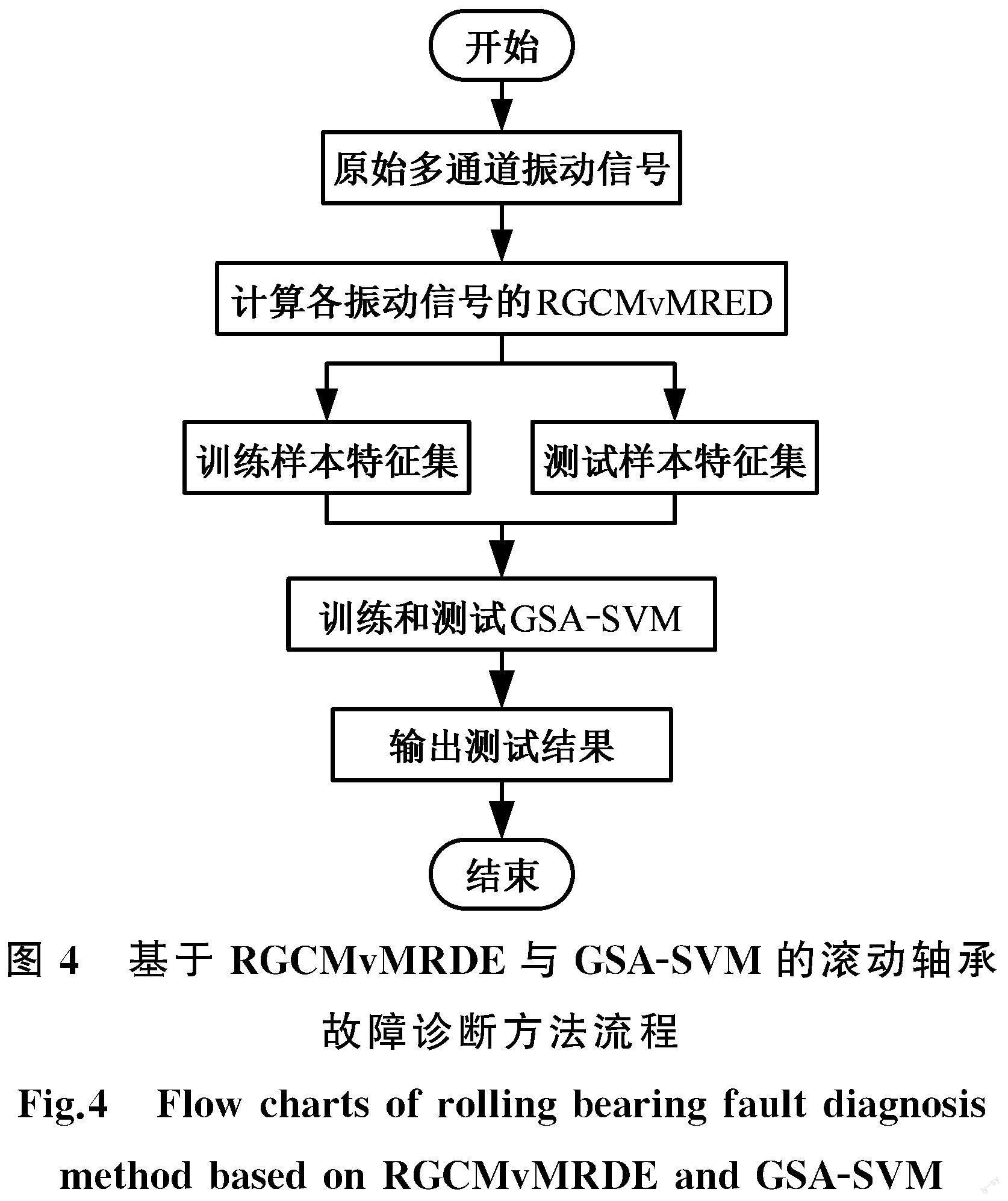
基于RGCMvMRDE方法特征提取的有效性与优势，本文提出了一种基于RGCMvMRDE和GSA-SVM的滚动轴承故障诊断方法，其計算流程如图4所示，具体步骤如下。

（1）考虑存在p种不同的滚动轴承状态数据，将其等分为q个样本，对所有样本进行RGCMv-MRDE特征提取，并选择一定数量的RGCMv-MRDE作为特征向量。

（2）从不同样本的特征向量中随机选取i个构建训练样本特征集，剩余部分则构建测试样本数据集。

（3）利用训练样本的故障特征向量对基于GSA-SVM建立的多故障分类器进行训练，得到训练模型。

（4）利用训练模型对测试数据集进行测试，依据分类模型输出结果判断滚动轴承的故障类型及故障程度。

2.3 公开数据集验证

将RGCMvMRDE方法用于分析美国凯斯西储大学（case western reserve university， CWRU）轴承数据中心的滚动轴承数据，滚动轴承故障实验平台如图5所示。该实验平台由电机、扭矩传感器、测功机和控制电子设备（图中未显示）组成。实验过程中，电机转速为1730 r/min，采样频率为12 kHz。在此条件下采集到正常（normal，简称NORM）、0.3556 mm内圈故障（inner race fault，IRF）、0.3556 mm外圈故障（outer race fault，ORF）和0.5334 mm滚动体故障（rolling element fault，REF）4种状态的振动信号，各20组数据，数据长度为2048，4种状态轴承的振动信号时域波形如图6所示。

从图6中不易发现正常与故障振动信号之间的明显区别，尤其是正常和滚动体故障信号。对4种状态振动信号进行RGCMvMRDE分析，每种数据不同样本RGCMvMRDE值的均值方差图见图7，其中嵌入维数m=3、类别数c=4、时延λ=1、最大尺度因子τmax=20。

由图7可以看出，首先，正常状态滚动轴承故障信号的RGCMvMRDE值低于相应的故障状态值，这是由于正常状态下的滚动轴承信号存在较多的随机波动，不规则性更高，随机性更强，而RDE定义为“与白噪声的距离”，因此，RGCMv-MRDE值较小；另一方面，具有局部故障的滾动轴承信号会产生规律性的冲击，不规则性较低，与白噪声相差较大，导致熵值增大。其次，在大多数尺度因子下，三种故障状态振动信号的RGCMv-MRDE值之间的关系为：EORF＞EIRF＞EREF。这是因为实际工作中滚动轴承在不同位置发生故障时，故障冲击引起的系统响应不同，因此，振动信号会表现出不同的复杂性。轴承外圈一般是固定的，当外圈发生局部故障时，振动信号的周期性冲击特性最为明显，使得复杂性程度降低，RGCMv-MRDE值增大。而轴承内圈通常与轴一起旋转，故障对振动信号的影响有限，没有外圈故障时振动信号的规则性突出，因此，内圈故障状态的RGCMvMRDE值小于外圈故障状态的RGCMv-MRDE值。同样地，当轴承滚动体沿着轴及自身旋转时，与内外圈故障相比，滚动体故障时振动信号的故障冲击不明显，随机性变化较小。因此，图7中不同故障状态振动信号的RGCMvMRDE值之间的关系符合实际，表明RGCMvMRDE可以有效区分不同故障类型，且具有较强的物理意义。

采用RGCMvMRDE提取故障特征后，利用GSA-SVM对故障模式进行识别。首先，对4种滚动轴承状态下各100组样本进行随机分类，得到200组训练样本和200组测试样本；其次，利用基于GSA-SVM建立的多故障分类器对训练样本的故障特征集合进行相关训练，其中，为了方便记录，分别标记“外圈故障、内圈故障、滚动体故障、正常”对应类别为1，2，3，4；最后，采用训练完成的多故障分类器对测试样本进行模式识别。最终诊断结果及混淆矩阵如图8所示，可以看出，本文所提基于RGCMvMRDE与GSA-SVM的诊断策略实现了全部样本的正确分类，对滚动轴承故障类型的识别精确且高效，最终识别率达到100%。

2.4 自制实验平台数据集验证

为了进一步验证RGCMvMRDE方法在特征提取上的优越性和通用性，本文采用江苏联益友测控技术有限责任公司为本单位定制的低速重载轴和轮系故障模拟实验台的实验数据对所提方法进行验证，实验平台如图9所示。在型号为6205 SKF的深沟球轴承上设置单点故障，采用传感器对X、Y、Z方向上的8种不同工况下的滚动轴承振动信号进行采集，采样频率为10 kHz，实验数据集的详细描述如表1所示，8种不同工况下的滚动轴承如图10所示。每种工况下的轴承振动信号分别采集三个通道数据，每个通道采集长度为2048的150个样本，将三个通道样本叠加构成一组样本，共得到150组样本，不同状态下轴承三通道（X，Y，Z）原始信号的时域波形如图11所示。

对于上述8种滚动轴承故障类型的数据，每种状态取150个样本，共1200个样本。首先，对每一个样本进行RGCMvMRDE分析，提取20个尺度的熵值作为故障特征向量；其次，对所有样本进行随机分类，选择70组数据构建训练样本数据集，剩余80组数据作为测试样本；最后，利用基于GSA-SVM建立的多故障分类器对训练样本数据集进行训练，并将所有测试样本输入到训练完成的分类器中进行测试。

同时，为了验证本文方法的优越性，采用MRDE、GMRDE和精细复合多元多尺度排列熵（refined composite multi-variate multi-scale permutation entropy， RCMvMPE）进行对比分析，其中MRDE、GMRDE和所提方法的参数设置一致。每种类型数据采用不同方法时的均值标准差如图12所示。

由图12可以看出，在大部分尺度上，对于基于RGCMvMRDE和GMRDE提取的熵均值曲线，故障振动信号的熵均值高于正常振动信号的熵均值，且针对不同类型故障引起的故障响应不同其复杂性表现也存在差异［26］，因此可以利用RGCMvMRDE来区分轴承的不同状态。不难发现RGCMvMRDE和GMRDE曲线的趋势类似，即广义多尺度分析具有一致的效果，但是RGCMvMRDE曲线更加平缓，熵值标准差更小，这说明精细复合分析具有更好的稳定性。此外，观察MRDE和RCMvMPE曲线可知，大多数尺度上不同故障类型样本及健康样本存在较高的重叠度，可区分性弱，但RCMvMPE曲线的标准差相对较小，进一步验证了精细复合分析的优越性。总体来说，基于RGCMvMRDE进行故障特征提取有一定优势，但仅以熵值曲线难以实现精准判断，故后续结合基于GSA-SVM建立的多故障分类器进行故障模式识别。

为了量化4种方法的特征提取效果，采用训练好的基于GSA-SVM建立的多故障分类器对基于测试样本构建的数据集进行测试，最终诊断结果和混淆矩阵如图13所示，可以看出，基于RGCMvMRDE与GSA-SVM的故障诊断方法的最终识别率可达到100%，不同故障类型及故障程度的滚动轴承均得到正确分类，GSA优化SVM的最优参数C、g分别为48.5026和0.1764。为了更直观地看出四种方法的区别，表2详细地给出了基于不同方法进行诊断的故障识别率，以及错分的样本信息和GSA-SVM的最优参数C、g。结合图13和表2可以看出，在不同对比方法中，基于RCMvMPE的GSA-SVM分类器的测试集实际分类与预测分类一致，故障识别率也达到100%；而基于MRDE和GMRDE的GSA-SVM分类器输出结果中分别有23个和13个样本被错分，故障识别率分别为95.8929%和97.6786%，均低于本文方法的识别率，验证了RGCMvMRDE相较于所对比方法的优越性。

为了进一步比较RGCMvMRDE和RCMv-MPE特征提取效果的优劣，针对不同数量的故障特征对两种滚动轴承故障诊断方法的识别率进行对比，将训练样本和测试样本的前20个故障特征输入到基于GSA-SVM建立的多故障分类器中，当故障特征个数输入不同时，基于RGCMvMRDE和RCMvMPE的故障诊断方法的最终识别率如

图14所示，图中详细给出了基于RGCMvMRDE与GSA-SVM以及基于RCMvMPE与GSA-SVM的滚动轴承故障诊断方法最终识别率的变化情况。由图14可知，无论故障特征数目输入多或少，本文所提的基于RGCMvMRDE的滚动轴承故障诊断方法的识别率均高于基于RCMvMPE的滚动轴承故障诊断方法的识别率，且识别率的变化趋势更为平稳。由此，对比结果验证了本文方法在特征提取上的有效性和稳定性，仅需要较少的特征向量即可完整地反映故障特征信息，取得良好的诊断效果。

3 结论

（1）提出了一种表征多通道数据复杂性的新算法——精细广义复合多元多尺度反向散布熵（RGCMvMRDE），克服了现有多尺度反向散布熵（MRDE）粗粒化过程中的不足，并通过不同类型噪声的仿真实验研究了RGCMvMRDE参数的选择及影响。

（2）将RGCMvMRDE应用于滚动轴承实验数据分析，结果表明，RGCMvMRDE能够高质量地提取故障特征，有效区分健康轴承和故障轴承以及不同故障类型的轴承。

（3）提出了一种基于RGCMvMRDE与引力搜索算法优化支持向量机（GSA-SVM）的滚动轴承故障诊断方法，并采用实测数据对所提方法的有效性进行了验证，结果表明：所提方法能够有效提取出轴承的各种故障特征信息，且在诊断效果和区分性能等方面优于MRDE、广义多尺度反向散布熵（GMRDE）和精细复合多元多尺度排列熵（RCMv-MPE）方法。

参考文献：

［1］ 唐贵基， 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用［J］. 西安交通大学学报， 2015， 49（5）：73-81.

TANG Guiji， WANG Xiaolong. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing［J］. Journal of Xian Jiaotong University， 2015， 49（5）：73-81.

［2］ LEI Y G， QIAO Z J， XU X F， et al. An Underdamped Stochastic Resonance Method with Stable-state Matching for Incipient Fault Diagnosis of Rolling Element Bearings［J］. Mechanical Systems and Signal Processing， 2017， 94（18）：148-164.

［3］ 胥永刚， 张志新， 马朝永， 等. 改进奇异谱分解及其在轴承故障诊断中的应用［J］. 振动工程学报， 2019， 32（3）：540-547.

XU Yonggang， ZHANG Zhixin， MA Chaoyong， et al. Improved Singular Spectrum Decomposition and Its Applications in Rolling Bearing Fault Diagnosis［J］. Journal of Vibration Engineering， 2019， 32（3）：540-547.

［4］ MOSTAFA R， MOHAMMAD R A， HAMED A. Application of Dispersion Entropy to Status Characterization of Rotary Machine［J］. Journal of Sound and Vibration， 2019， 438：291-308.

［5］ YAN R Q， GAO R X. Approximate Entropy as a Diagnostic Tool for Machine Health Monitoring［J］. Mechanical Systems and Signal Processing， 2007， 21（2）：824-839.

［6］ 何文平， 何涛， 成海英， 等. 基于近似熵的突变检测新方法［J］. 物理学报， 2011， 60（4）：820-828.

HE Wenping， HE Tao， CHENG Haiying， et al. A New Method to Detect Abrupt Change Based on Approximate Entropy［J］. Acta Physice Sinica， 2011， 60（4）：820-828.

［7］ 杨望灿， 张培林， 王怀光， 等. 基于EEMD的多尺度模糊熵的齿轮故障诊断［J］. 振动与冲击， 2015， 34（14）：163-167.

YANG Wangcan， ZHANG Peilin， WANG Huai-guang， et al. Gear Fault Diagnosis Based on Multi-scale Fuzzy Entropy of EEMD［J］. Journal of Vibration Engineer，2015， 34（14）：163-167.

［8］ 孟宗， 季艷， 闫晓丽. 基于DEMD和模糊熵的滚动轴承故障诊断方法研究［J］. 计量学报， 2016， 37（1）：56-61.

MENG Zong， JI Yan， YAN Xiaoli， et al. Rolling Bearing Fault Diagnosis Based on Differential-based Empirical Mode Decomposition and Fuzzy Entropy［J］. Acta Metrologica Sinica， 2016， 37（1）：56-61.

［9］ YAN R Q， LIU Y B， GAO R X. Permutation Entropy：A Nonlinear Statistical Measure for Status Characterization of Rotary Machines［J］. Mechanical Systems and Signal Processing， 2012， 29（5）：474-484.

［10］ 丁闖， 张兵志， 冯辅周， 等. 局部均值分解和排列熵在行星齿轮箱故障诊断中的应用［J］. 振动与冲击， 2017， 36（17）：55-60.

DING Chuang， ZHANG Bingzhi， FENG Fuzhou， et al. Application of Local Mean Decomposition and Permutation Entropy in Fault Diagnosis of Planetary Gearboxes［J］. Journal of Vibration and Shock，2017， 36（17）：55-60.

［11］ ROSTAGHI M， AZAMI H. Dispersion Entropy：A Measure for Time Series Analysis［J］. IEEE Signal Processing Letters， 2016， 23（5）：610-614.

［12］ 付文龙， 谭佳文， 王凯. 基于VMD散布熵与改进灰狼优化SVDD的轴承半监督故障诊断研究［J］. 振动与冲击， 2019， 38（22）：190-197.

FU Wenlong， TAN Jiawen， WANG Kai. Semi-supervised Fault Diagnosis of Bearing Based on the VMD Dispersion Entropy and Improved SVDD with Modified Grey Wolf Optimizer［J］. Journal of Vibration Engineer，2019， 38（22）：190-197.

［13］ LI Y， GAO X， WANG L. Reverse Dispersion Entropy：a New Complexity Measure for Sensor Signal［J］. Sensors， 2019， 19（23）：1-14.

［14］ 王余奎， 李洪儒， 叶鹏. 基于多尺度排列熵的液压泵故障识别［J］. 中国机械工程， 2015， 26（4）：518-523.

WANG Yukui， LI Hongru， YE Peng. Fault Identification of Hydraulic Pump Based on Multi-scale Permutation Entropy［J］. China Mechanical Engineering，2015， 26（4）：518-523.

［15］ LI Y， JIAO S， GENG B， et al. Research on Feature Extraction of Ship-radiated Noise Based on Multi-scale Reverse Dispersion Entropy［J］. Applied Acoustics， 2021， 173（1）：107737.

［16］ COSTA M， GOLDBERGER A. Generalized Multi-scale Entropy Analysis：Application to Quantifying the Complex Volatility of Human Heartbeat Time Series［J］. Entropy， 2015， 17（3）：1197-1203.

［17］ 丁嘉鑫， 王振亚， 姚立纲， 等. 广义复合多尺度加权排列熵与参数优化支持向量机的滚动轴承故障诊断［J］. 中国机械工程， 2021， 32（2）：147-155.

DING Jiaxin， WANG Zhenya， YAO Ligang， et al. Rolling Bearing Fault Diagnosis Based on GCMWPE and Parameter Optimization SVM［J］. China Mechanical Engineering， 2021， 32（2）：147-155.

［18］ 刘武强， 申金星， 杨小强. 基于精细复合多元多尺度加权排列熵与流形学习的滚动轴承故障诊断［J］. 轴承， 2021（9）：54-60.

LIU Wuqiang， SHEN Jinxing， YANG Xiaoqiang. Fault Diagnosis for Rolling Bearing Based on RCMMWPE and Manifold Learning［J］. Bearing，2021（9）：54-60.

［19］ AZAMI H， ESCUDERO J. Refined Composite Multivariate Generalized Multi-scale Fuzzy Entropy：A Tool for Complexity Analysis of Multichannel Signals［J］. Physical A， 2017， 465：261-276.

［20］ WEI D， ZHANG S Q， HU M F， et al. Intelligent Fault Diagnosis of Wind Turbine Gearboxes Based on Refined Generalized Multi-scale State Joint Entropy and Robust Spectral Feature Selection［J］. Nonlinear Dynamics， 2022， 107：2485-2517.

［21］ SARAFRAZI S， NEZAMABADI-POUR H. Facing the Classification of Binary Problems with a GSA-SVM Hybrid System［J］. Mathematical and Computer Modelling， 2013， 57（1/2）：270-278.

［22］ XUE H， BAI Y， HU H， et al. A Novel Hybrid Model Based on TVIW-PSO-GSA Algorithm and Support Vector Machine for Classification Problems［J］. IEEE Access， 2019， 7：27789-27801.

［23］ 李森娟， 張萍， 岳大为， 等. 基于支持向量机的风电机组故障预测［J］. 计算机仿真， 2022， 39（5）：84-88.

LI Senjuan， ZHANG Ping， YUE Dawei， et al. Fault Prediction of Wind Turbine Based on Support Vector Machine［J］. Computer Simulation，2022， 39（5）：84-88.

［24］ WANG Z Y， YAO L G， CAI Y W. Rolling Bearing Fault Diagnosis Using Generalized Refined Composite Multi-scale Sample Entropy and Optimized Support Vector Machine［J］. Measurement， 2020， 156：107574.

［25］ RASHEDI E， NEZAMABADI-POUR H， SARYAZDI S. GSA：A Gravitational Search Algorithm［J］. Information Sciences， 2009， 179（13）：2232-2248.

［26］ MOSHREFZADEH A. Condition Monitoring and Intelligent Diagnosis of Rolling Element Bearings under Constant/Variable Load and Speed Conditions［J］. Mechanical Systems and Signal Processing， 2021， 149：107153.