兼顾时频域特征量提取的非线性油气悬架参数识别
伍建伟 孙蓓蓓 江秋博 陈林
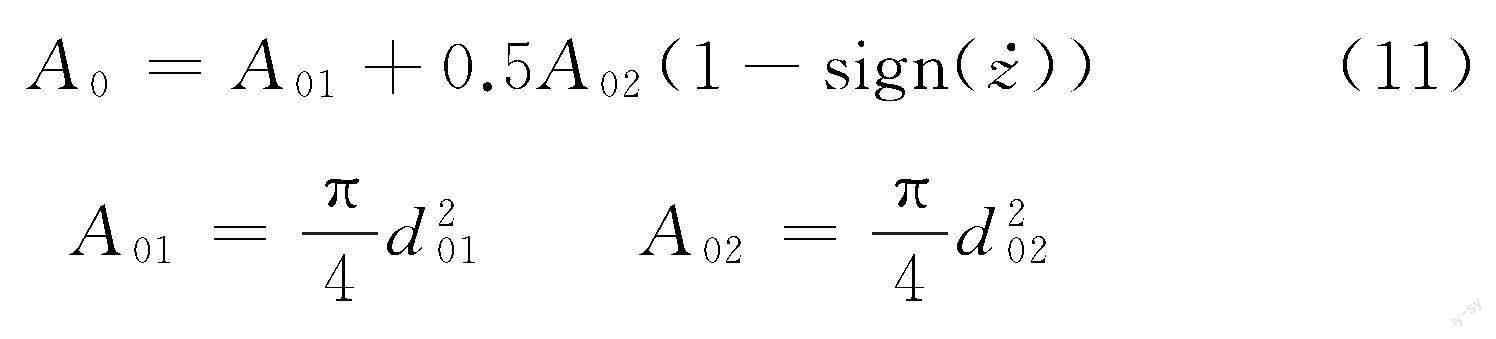
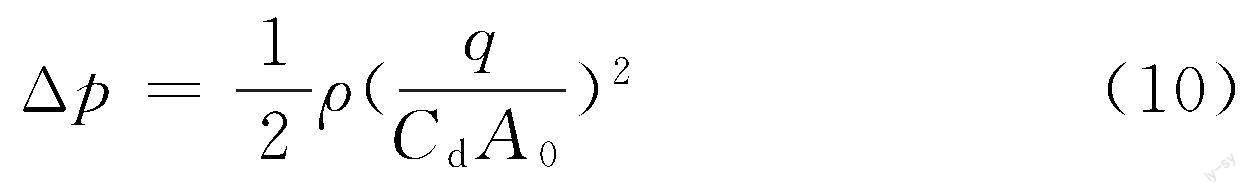
摘要:针对完全基于时域或完全基于频域的非线性参数识别方法的局限性,提出了一种兼顾时频域特征量提取的非线性油气悬架参数识别方法。在建立含非线性油气悬架车辆动力学仿真模型的基础上,采用快速傅里叶逆变换法获得标准路面不平度等级的输入激励,结合小波分析和滤波处理提取实验结果的时频域特征量,构建非线性油气悬架参数识别的优化模型,通过最小化仿真结果与实验结果在时频域的特征量,实现了非线性油气悬架参数在实际工况下的准确识别。识别的定量与定性分析表明了识别结果的准确可靠。通过将路面时域建模技术、小波滤波技术和优化模型构造方法与模拟退火算法的有机结合,为非线性悬架系统的参数识别提供了一种有效可靠的方法。
关键词:油气悬架;参数识别;路面时域建模;快速傅里叶逆变换法;小波分析;模拟退火算法
中图分类号:U463.33
DOI:10.3969/j.issn.1004132X.2023.11.005
Parameter Identification of Nonlinear Hydro-pneumatic Suspensions Basedon Feature Extraction in Time-frequency Domain
WU Jianwei1,2 SUN Beibei2 JIANG Qiubo2 CHEN Lin2
1.School of Mechanical and Electrical Engineering,Guilin University of Electronic Technology,
Guilin,Guangxi,541004
2.School of Mechanical Engineering,Southeast University,Nanjing,211189
Abstract: Considering the limitation of the nonlinear parameter identification method based entirely on the time domain or the frequency domain, a parameter identification method for nonlinear hydro-pneumatic suspensions was proposed based on feature extraction in time-frequency domain. The vehicle dynamics simulation models with nonlinear hydro-dynamic suspensions were established, the IFFT method was used to obtain the road excitation with the level of the standard road surface, the feature quantities in the time-frequency domain of the experimental results were extracted by combining with the wavelet analysis and filtering, and an optimization model for identification of nonlinear hydro-pneumatic suspension parameters was constructed. By minimizing the feature quantities of simulation and experimental results in the time-frequency domain, the nonlinear parameters of the hydro-pneumatic suspensions were accurately identified under actual conditions. The quantitative and qualitative analyses of the identification show that the identification results are accurate and reliable. By combining road time domain modeling, wavelet filtering technology and construction method for the optimization model with simulated annealing algorithm, an effective and reliable identification method was provided for parameter identification of nonlinear suspension systems.
Key words: hydro-pneumatic suspension; parameter identification; time-domain model on road; inverse fast Fourier transform(IFFT) method; wavelet analysis; simulated annealing algorithm
0 引言
準确的悬架参数能够提高动力学仿真的模拟精度,实现车辆状态及性能的精准预测,有效地完成系统结构参数改进和实现主动控制器设计。油气悬架是一种以油液传递压力、以惰性气体(通常为氮气)作为弹性介质的汽车悬架,它将传统悬架的弹性元件和减振器功能集于一体,具有结构紧凑、布置简单等优点,拥有较为理想的非线性特性,在国内外的特种车辆、高级轿车以及工程车辆上应用十分广泛[1-3]。油气悬架设计安装完成后,其动力学特性还会受到如下各种因素的影响:①加工、安装等因素;②阻尼孔和单向阀受孔径、厚度和开启阀的影响,它们的有效作用面积及其流量系数难以准确地确定;③油液的局部或沿程压力损失系数会发生一定的变化[4];④气体在腔室中的压缩和膨胀效应无法理想化为完全绝热或完全等温过程,即气体多变指数会发生变化[5];⑤摩擦力受润滑条件、活塞与活塞孔加工精度的影响。这些因素会使悬架的设计参数与实际参数产生较大的偏差,严重影响系统在动力学仿真中的模拟精度,增加了优化与控制的难度。
目前悬架参数的获取主要有三种途径:一是根据力学的基本原理建立其数学模型,结合结构设计尺寸计算得到;二是根据实验平台进行动态测试,結合软件对数据处理得到;三是根据少量输入与输出数据,结合给定模型结构进行参数识别得到。由于模型的简化、加工安装的误差等原因,第一种途径得到的车辆动力学参数往往与实际情况相差较大,大多都需要作进一步的修正。第二种途径由于约束等条件的不同,组装前测试参数与安装后的实际参数可能存在较大差异,并且它还需要高昂的经济成本和时间成本。第三种途径只需要较少的实验就可以完成给定模型结构的参数识别,甚至可以在整个系统组装完毕后进行参数识别,可能是最可靠的一种方式[6]。
悬架参数识别一直是一个活跃的研究领域,发展了各种各样用于识别车辆悬架参数的技术和方法,包括最小二乘法、极大似然估计法、频率响应法和卡尔曼滤波参数估计法等[7-8]。THITE等[9]利用矩阵逆方法实现了频域下悬架参数的估计,有效地减小了测量噪声的影响。CALDEIRA等[10]通过垂向和俯仰运动加速度的估计值与伪实验数据的二次方误差的最小化,采用基于粒子群算法的反问题技术和随机限制窗算法对履带车辆的悬架刚度和阻尼系数参数进行了估计。XU等[11]根据垂直轨道的车辆模型提出了两种扩展卡尔曼滤波器(EKF)和两种无迹卡尔曼滤波器(UKF),并用于二次悬架参数估计,通过线性和非线性模型进行仿真实验来研究两种估计方法的性能。李翠梅等[12]为解决传统线性及非线性系统参数识别的问题,根据最小二乘法原理提出了具有物理意义的非线性系统线性及非线性参数的识别方法。ZHAO等[13]提出了一种基于多目标遗传算法优化的座椅乘员系统振动参数快速辨识方法,该方法能够根据振动试验结果,快速准确地辨识出5自由度集中质量模型的座椅系统参数。
这些悬架参数的识别方法大多数完全基于时域或完全基于频域,主要还是用于线性参数的识别。对于一些动态识别方法,由于要兼顾计算成本,其识别精度一般不高。除此之外,为了表征系统非线性而构造的黑箱辨识模型,由于没有考虑到系统本身内在机理,其应用范围往往十分有限。为了保证识别结果的可靠性,根据能够反映系统内在特征的机理模型,综合考虑时域和频域的响应结果,利用少量的实验数据实现其参数的准确识别,是非线性悬架识别领域的研究趋势,研究人员对此进行了一定的探索[14-15]。
在综合考虑时域和频域特征量的基础上,如何根据少量的实验数据对部分参数已知的非线性油气悬架进行准确可靠的参数识别,是本文所要解决的一个关键性问题。对此,本文在建立含非线性油气悬架车辆动力学模型的基础上,摈弃传统的基于线性随机振动理论的频域分析方法,采用快速傅里叶逆变换(IFFT)法进行时域路面建模,构造关于实验结果在时频域下特征量的多目标优化模型,使用模拟退火优化算法来最小化仿真与实验结果所提取的特征量偏差,实现非线性油气悬架参数的准确识别。
1 含油气悬架的四分之一车辆动力学模型
1.1 四分之一车辆动力学模型
图1为四分之一车辆模型及其油气悬架(或称为油气悬挂或油气弹簧)结构简图。其中,mw、mb分别表示簧下质量和簧上质量;xg、xw、xb分别表示路面随机位移、簧下质量位移、簧上质量位移;kt为轮胎刚度。该图右侧为混合式单气室油气悬架结构简图,这种混合式油气悬架具有结构紧凑、设计灵活、成本低廉等特点,在工程车辆中应用十分广泛。
图1中油气悬架主要由缸筒、活塞杆和活塞组件组成。悬架缸内有两个腔,分别为Ⅰ腔和Ⅱ腔,活塞杆壁上开有常通节流孔和单向阀孔。油气悬架Ⅰ腔上部和Ⅱ腔充入油液,Ⅰ腔下部充入惰性气体,D和d分别表示缸筒内径和活塞杆外径。惰性气体起弹性元件的作用,油液在悬挂缸中起着能量传递、转移和控制的作用,另外还有润滑作用。由于悬挂缸内部高压氮气具有可压缩性,故活塞杆和缸筒的相对运动会造成气体体积的变化,从而吸收和释放能量。当悬挂液压缸处于压缩行程时,单向阀开启,缸内环形腔容积增大,液压油通过固定的阻尼孔口和单向阀口由Ⅰ腔流向Ⅱ腔,运动受到的阻尼力较小,此时气腔内的气体被压缩,从而吸收能量;当悬挂液压缸处于拉伸行程时,单向阀阀口关闭,环形腔内体积缩小,液压油只通过阻尼孔由腔Ⅱ流向Ⅰ腔,运动受到的阻尼力较大,此时气腔内的气体膨胀,从而释放能量。
建立含密封摩擦的非线性油气悬架的受力数学模型,得到四分之一车辆模型的动力学方程:
式中,F为油气悬架所产生的非线性作用力。
1.2 油气悬架受力的数学模型
两个腔室Ⅰ和Ⅱ的有效截面积为
在静平衡下,有
式中,ps0为静平衡位置Ⅰ腔下部气室的压力。
(1)整个腔室的受力方程。以油缸为研究对象,有
F=p1A1-p2A2-Ff(5)
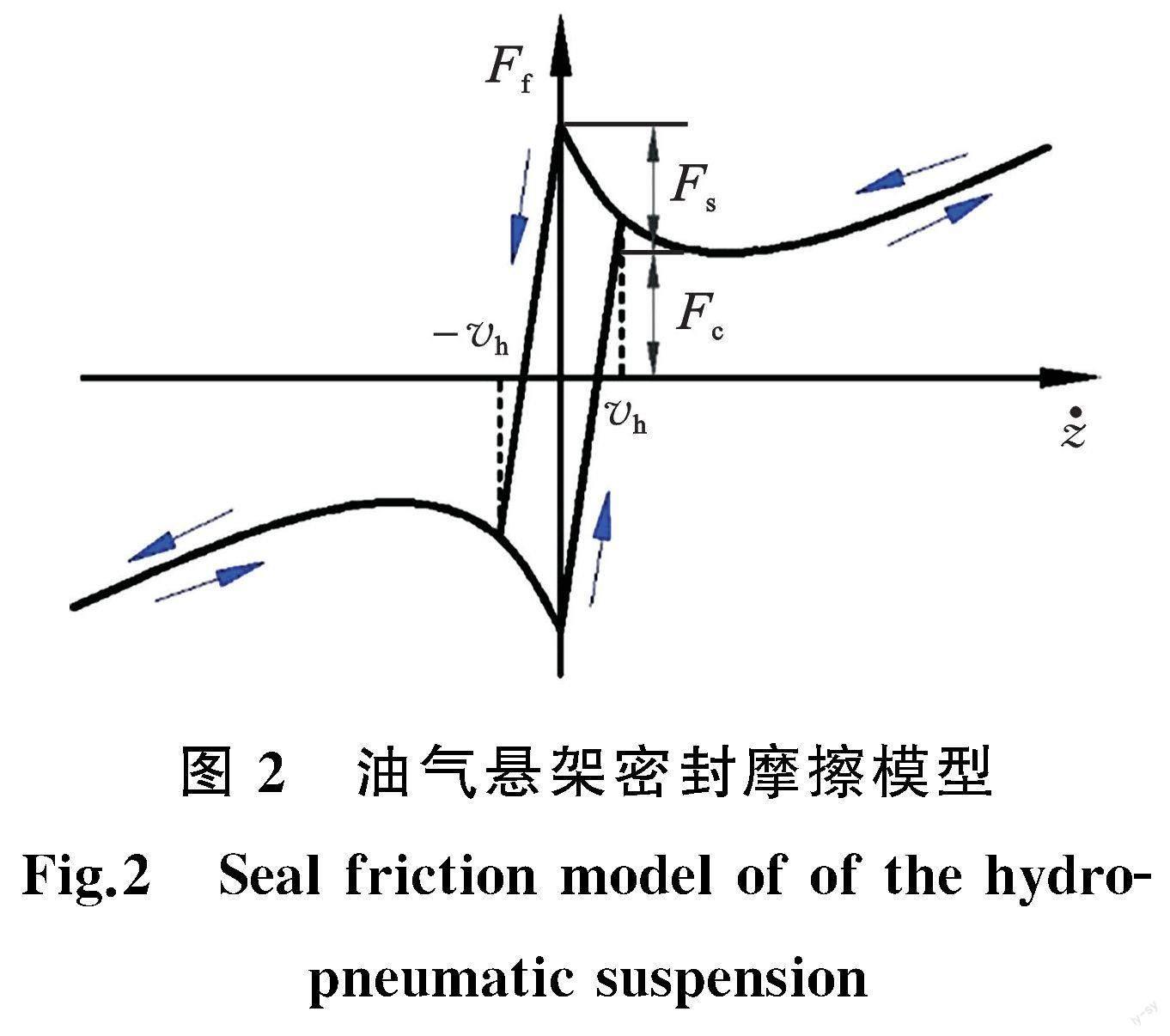
式中,p1、p2分别为Ⅰ腔和Ⅱ腔内的压力;Ff为悬架的密封摩擦力。
(3)油气悬架气腔内的气体为氮气,它的性质和理想气体相近,其状态变化过程可以表示为
pg1Vr1=pg0Vr0(8)
其中,V0、V1分别为初始和任意状态下的气体体积;pg0、pg1分别为初始和任意状态下相应的气体压力;r为气体多变指数。
在快速加载时,气体状态变化为绝热过程,这时r=1.4;当缓慢加载时,气体状态变化为等温过程,这时r=1。实际自卸车道路颠簸,悬架多为快速加载,气体多变指数取r=1.4。
(4)Ⅰ腔Ⅱ腔的压力差为
Δp=p1-p2(9)
其中,Δp因悬架缸阻尼孔和单向阀的阻尼而产生。
(5)节流孔的数学模型。根据液体经过薄壁小孔的节流理论[19],有
式中,q为流量;Cd为流量系数;A0为小孔截面积;ρ为流体密度。
对于含有单向阀的阻尼孔,有
式中,A01、A02分别为常通阻尼孔和单向阀的有效截面积;d01、d02分别为常通阻尼孔和单向阀的等效直径。
将式(11)代入式(10)中,有
油气立柱处于压缩状态时,单向阀打开,反之单向阀关闭。
(6)流量q的计算。当活塞杆相对缸筒向上移动z时,腔Ⅱ液体体积增加量ΔV2=A2z,左右两边对时间求导,得到
(7)整个腔室的受力可以写成
F=p1A1-(p1-Δp)A2-Ff=
p1(A1-A2)+ΔpA2-Ff(14)
利用式(12)和式(13),可以将式(5)写成
可以看出:整个油气立柱所受到的力由气体产生的弹性力Fk、油液产生的阻尼力Fc和密封摩擦力Ff所组成。
1.3 基于IFFT法的路面时域建模
传统随机线性振动理论并不适用于含非线性油气悬架特性的车辆动力学模型,研究人员通常使用时域的方法进行求解。目前,路面不平度时域建模的主要方法有谐波叠加法、滤波白噪声法、自回归滑动平均模型(ARMA)法、泊松(Poisson)法和IFFT法等。IFFT法具有高效、快速、重构精度高的优点,可用于建立路面时域模型[20-21]。需要注意的是:发动机的基频较大,通过滤波后对结果的影响较小,因此在仿真中忽略了发动机激励的影响。
国际标准化组织和我国国家标准均建议路面不平度的统计特性用功率谱密度来表示[22-23],时间频率功率谱密度可以表示为
式中,Gq(n0)为不平度指数;n0为空间参考频率;v为车辆行驶的速度;f为时间频率。
根据功率谱和幅值谱的关系,Gq(f)可以表示为
式中,Xg(f)为路面不平度的幅值谱;xg(t)为路面不平度关于时间的路面不平度位移;T为总采样时间。
相位谱可以视为均匀随机分布,范围为[0,π]。根据式(17),通过离散采样计算得到幅值谱,再通过IFFT即可获得路面不平度关于时间的变化关系。
在车速为20 km/h条件下,国家标准路面等级为C和D的路面不平度的时域曲线如图3所示。可以验证,此时路面不平度位移的均方根值分別为0.015 m、0.0301 m,与国家标准的结果一致[24]。
1.4 车辆动力学仿真参数
根据现有的材料参数、结构参数、安装参数和实验数据,再结合经验取值,可以确定含非线性油气悬架的四分之一车辆模型参数,如表1所示。路面实测研究表明,非公路矿山路面多为D级路面[25-27],故采用国家标准D级路面作为四分之一车辆动力学仿真的输入。
2 车辆振动测试实验
图4所示为整车振动测试方案及其布置。测试分析仪器主要包括德国 M+P 信号采集及分析系统、PCB 振动传感器和SO Analyze等。加速度传感器的测点分别布置在油气悬架的上下端,分别测量簧上和簧下质量的加速度响应。实验中,采样频率设置为512 Hz,车辆在路面上匀速行驶速度为20 km/h,测量得到簧下和簧上质量的加速度响应。考虑到SO Analyze显示效果不佳,故将采集的实验数据导出到MATLAB中作进一步处理,如图5所示。假设车辆左右轮和前后轮之间的路面大致相同,车辆可以近似地简化为四分之一车辆模型。通过对四分之一车辆模型进行仿真并与实验结果进行比较,可识别车辆系统非线性油气悬架等参数。
3 基于小波分析的实验数据处理
3.1 小波分析理论
小波分析是现代常用的信号处理方法,它克服了傅里叶变换的不足,能够同时在时域和频域上表示信号的特征[28-29]。通过小波分析,原始信号可以分解为一系列具有不同频段的子信号,即
f(t)=an(t)+dn(t)+dn-1(t)+…+d2(t)+d1(t)(18)
式中,f(t)为原始信号;a为低频信号的近似部份;d为高频细节部分;下标n为分解的层数。
利用小波分解的树形图见图6,它表示三层小波分解,图中Fs表示原始信号的采样频率。由图6可以看出,小波的每层分解是将信号分解为低频和高频各占一半带宽的频带,而高频部分将不再分解。因此,对于给定的一个信号,可以确定一个合适的分解层次,使所关心的频率成分落入某一频带中,用于进一步地分析。
3.2 实验数据处理
本文所建立的车辆模型输入仅来自路面不平激励,因此,为了保证仿真结果尽可能地贴近于实验结果,结合路面不平的波长和车速,通过小波分析对振动测试得到的高频信号进行滤波,获得所关注频段的重构时域信号。根据文献[25,30]中实测数据,非公路的空间频率范围主要为0.011~1.6 m-1。根据矿用卡车常用速度范围[0,60 km/h],得到路面的时间频率范围为[0,26.7 Hz]。
对第三层低频信号进行小波分析重构后,得到的时域和频域曲线如图7和图8所示,将其进行快速傅里叶变换,得到[0,32 Hz]范围内簧上和簧下质量加速度的重构曲线。
重构曲线的特征量如表2所示。
4 非线性油气悬架参数识别的优化模型
车辆在安装完成后,根据某些部件实验测试结果、结构设计尺寸以及部分传感器数据,可以确定车辆动力学的大多数仿真参数,但是,很多非线性油气悬架的参数值并不十分准确,如油液经过阻尼孔和单向阀时的有效截面积、气体的多变指数、库仑摩擦力等。此时,可以利用结构参数及其已有的经验数据确定它们所处的范围,根据实验测试结果对这些参数进行进一步的修正,实现非线性油气悬架参数在实际路况下的准确识别。对此,根据实验得到时频域内的特征量,构造如下的优化模型。
(1)设计变量
X=(d01,d02,Cd,r,Fc,Fs)T(19)
(2)目标函数。为了保证仿真系统能够全面地反映实验响应结果,使该识别结果更具有普遍意义,目标函数设计为仿真与实验在时域和频域内的多个特征量最小化的形式,形成一个多目标优化问题。为各个特性量引入相应的权重,建立如下目标函数:
f(X)=w1(arms1-2.578)2+w2(arms2-1.757)2+
w3(amin1+12.009)2+w4(amax1-16.166)2+
w5(amin2+6.507)2+w6(amax2-6.671)2+
w7(fmax1-1.672)2+w8(fmax1-1.672)2(20)
其中,arms1、arms2、amin1、amax1、amin2、amax2、fmax1、fmax2为四分之一车辆模型仿真及其相应的数据处理得到的特征量,分别为簧下质量加速度均方根值、簧上质量加速度均方根值、簧下质量加速度的最小值、簧下质量加速度的最大值、簧上质量加速度的最小值、簧上质量加速度的最大值、频域内簧下质量加速度幅值谱的最大幅值对应的频率、频域内簧上质量加速度幅值谱的最大幅值对应的频率;w1、w2、…、w8为相应特征量的权重。综合考虑,权重系数的取值如表3所示。
(3)约束函数。约束函数主要是边界约束,即根据结构参数和先验取值可获得设计变量的最大和最小值。综合考虑,设计变量的取值范围如表4所示。
5 非线性油气悬架参数识别结果
由于时域信号在进行傅里叶变换时,其幅值谱会受到采样频率和采样总时间的影响,因此,为了保证仿真与实验结果在幅值谱上的可比性,将仿真的采样频率和采样总时间设置与实验相同,即512 Hz和60 s。
与遗传算法等其他智能算法相比,模拟退火算法具有一定优势和特殊的功能。模拟退火算法与初始值无关,即算法求得的解与初始解(算法迭代的起点)的选取无关;它在搜索过程中可跳出某局部最优解,具有渐进收敛性,已在理论上被证明是一种以概率收敛于全局最优解的优化算法[31-32]。因此,为减小初始值选取的影响,保证能够获得全局最优解,本文采用模拟退火算法对识别模型进行优化求解,优化迭代过程如图9所示。仿真与实验特征量最小化的识别结果如表5所示。
将识别得到的非線性油气悬架参数输入到含油气悬架的四分之一车辆动力学模型中进行仿真,得到簧下和簧上质量加速度的仿真结果以及摩擦力特性曲线,如图10~图12所示。它们所对应的特征量如表6所示。
6 识别结果分析
6.1 定量分析
(1)非线性油气悬架参数的识别结果是准确、可靠的。由表6可以看出,仿真与实验结果得到的各个特征量都十分接近,并且仿真得到的时域和频域响应曲线与实验曲线相差很小,说明识别结果是准确、可靠的。
(2)非线性油气悬架的识别结果与实际情况相吻合。由表6可以看出,仿真所得到的簧上质量加速度均方根值小于对应的实验结果,且仿真所得到的簧下质量的加速度均方根值要大于对应的实验结果。出现这种情况的原因是:一方面,虽然已经根据路面频率范围对实验结果进行滤波,但发动机等激励同样会在这个频段产生一定的作用,导致簧上质量加速度的实验结果略大于仿真结果;另一方面,仿真中并没有考虑轮胎的阻尼,而轮胎阻尼是真实存在的,从而导致仿真所得到的簧下质量的加速度均方根值大于实验得到的结果。
(3)国家标准D级路面谱与实际路面谱存在一定区别。可以看出,簧上和簧下质量时域的最大和最小加速度与实验结果存在一定的偏差,仿真与实验的幅值谱中最大幅值对应的频率也存在不小的偏差。可能的原因是:一方面,国家标准的D级路面谱与实际车辆振动测试的路面谱并不完全相同;另一方面,当车辆在不平路面运动时,车辆会产生侧倾和俯仰,会对车辆时域响应的最大和最小值产生影响。但整体从时域和频率的特征量来看,基本上都是吻合的,说明参数识别结果在实际中是可行的、有效的。
(4)间接结果与实测结果也十分吻合。根据非线性油气悬架的识别结果,可以得到D级路面下系统的响应,从而得到油缸的压力范围等性能指标,可以得到压力范围为3.459~7.276 MPa,这与实测的结果基本一致。
6.2 定性分析
此时,根据实验得到的簧下和簧上质量加速度响应结果,通过数据的重采样、截断、滤波、去均值等数据处理操作,利用MATLAB的系统辨识模块可得到线性化的结果,如图13所示。由于30~120 s为稳定行驶路面,因此截取了部分该段数据用于系统的识别(图13)。为清晰地对比实验与线性系统识别结果,进一步显示了54~60 s段的曲线,如图14所示。可以看出,线性系统辨识结果与实验曲线比较吻合,估计模型的最终预测误差(final prediction error for estimated model,FPE)为1.346。从幅值和趋势上可以看出,系统识别结果基本上能够反映它的本质特性。
根据系统辨识得到的传递函数表达式,结合已知的簧上质量可得悬架的线性等效刚度和线性等效阻尼系数分别为1166 kN/m、130 kN·s/m。此外,通过对优化模型识别的非线性油气悬架参数进行仿真,得到悬架的相对位移与速度响应,可以确定油气悬架刚度和阻尼系数的变化范围分别为493.63~1738.89 kN/m、0~297.66 kN·s/m。可以看出,系统辨识得到的线性等效刚度和阻尼系数大约就处于该范围内的中值位置,这也定性地表明了本文非线性油气悬架参数识别结果的合理性。
7 结语
本文在建立含非线性油气悬架车辆动力学仿真模型的基础上,通过将路面时域建模技术、小波滤波技术和优化模型构造方法与模拟退火算法的有机结合,实现了非线性油气悬架参数在实际工况下的准确识别,为非线性悬架系统的参数识别提供了一种有效可靠的识别方法。所提方法从频域和时域上有效地表征系统的特征,提高了辨识结果的可靠性,为后续的动力学建模、仿真及其控制相关工作提供有力保障。
参考文献:
[1] 李仲兴, 郭子权, 王传建, 等. 越野车用两级压力式油气弹簧的建模与仿真[J]. 振动·测试与诊断, 2017, 37(3):512-517.
LI Zhongxing, GUO Ziquan, WANG Chuanjian, et al. Modeling and Simulating of a Two Stage Pressure Hydro-pneumatic Spring for Off-road Vehicle[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(3):512-517.
[2] WU W, TANG H, ZHANG S, et al. High-precision Dynamics Characteristic Modeling Method Research Considering the Influence Factors of Hydropneumatic Suspension[J]. Shock and Vibration, 2020, 8:1-21.
[3] YANG L, WANG R, MENG X, et al. Performance Analysis of a New Hydropneumatic Inerter-based Suspension System with Semi-active Control Effect[J]. Journal of Automobile Engineering, 2020, 234:1883-1896.
[4] 赵敬凯, 谷正气, 张沙, 等. 矿用自卸车油气悬架力学特性研究与优化[J]. 机械工程学报. 2015, 51(10):112-118.
ZHAO Jingkai, GU Zhengqi, ZHANG Sha, et al. Research and Optimization on the Mechanical Property of Mining Dump Trucks Hydro-pneumatic Suspension[J]. Journal of Mechanical Engineering, 2015, 51(10):112-118.
[5] LI Z, WANG Y, DU H, et al. Modelling and Analysis of Full-vehicle Hydro-pneumatic Suspension System Considering Real-gas Polytropic Process[J]. Mechanical Systems and Signal Processing, 2022, 165(1):1-21.
[6] BEST M C, GORDON T J. Suspension System Identification Based on Impulse-momentum Equations[J]. Vehicle System Dynamics, 1998(29S):598-618.
[7] CUI Y, KURFESS T R. Vehicle Parameter Identification for Vertical Dynamics[J]. Journal of Dynamic Systems Measurement and Control—Transactions of the ASME, 2015, 137(2):1-9.
[8] ELINGER J, ROGERS J. Information Theoretic Causality Measures for System Identification of Mechanical Systems[J]. Journal of Computational and Nonlinear Dynamics, 2018, 13(7):1-12.
[9] THITE A N, BANVIDI S, IBICEK T, et al. Suspension Parameter Estimation in the Frequency Domain Using a Matrix Inversion Approach[J]. Vehicle System Dynamics, 2011, 49(12):1803-1822.
[10] CALDEIRA A B, de CARVALHO M S, da COSTA NETO R T. Estimation of Tracked Vehicle Suspension Parameters[J]. Acta Scientiarum—Technology, 2017, 39(1):51-57.
[11] XU B, ZHANG J, GUAN X. Estimation of the Parameters of a Railway Vehicle Suspension Using Model-based Filters with Uncertainties[J]. Journal of Rail and Rapid Transit, 2015, 229(7):785-797.
[12] 李翠梅, 周洋. 非線性悬架系统的最小二乘参数识别方法[J]. 机械设计与制造, 2020(9):62-65.
LI Cuimei, ZHOU Yang. The Least Squares Method Based Parameter Estimation of Nonlinear Vehicle Suspension Systems[J]. Machinery Design & Manufacture, 2020(9):62-65.
[13] ZHAO Y, ALASHMORI M, BI F, et al. Parameter Identification and Robust Vibration Control of a Truck Drivers Seat System Using Multi-objective Optimization and Genetic Algorithm[J]. Applied Acoustics, 2021, 173(1):1-13.
[14] BURDZIK R. Multidimensional Identification of Resonances Analysis of Strongly Nonstationary Signals, Case Study:Diagnostic and Condition Monitoring of Vehicles Suspension System[J]. Applied Acoustics, 2019, 144:51-63.
[15] WANG C, ZHANG J, ZHU H P. A Combined Method for Time-varying Parameter Identification Based on Variational Mode Decomposition and Generalized Morse Wavelet[J]. International Journal of Structural Stability and Dynamics, 2020, 20(7):1-24
[16] 金纯, 孙会来, 张文明, 等. 工程车辆油气悬架分数阶建模与特性分析[J]. 农业机械学报, 2014, 45(5):16-21.
JIN Chun, SUN Huilai, ZHANG Wenming, et al. Fractional Modeling and Characteristic Analysis of Hydro-pneumatic Suspension for Construction Vehicles[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5):16-21.
[17] PAN Q, LI Y, HUANG M. Control-oriented Friction Modeling of Hydraulic Actuators Based on Hysteretic Nonlinearity of Lubricant Film[J]. Mechatronics, 2018, 53:72-84.
[18] YIN Y, RAKHEJA S, YANG J, et al. Characterization of a Hydro-pneumatic Suspension Strut with Gas-oil Emulsion[J]. Mechanical Systems and Signal Processing, 2018, 106:319-333.
[19] 李兵, 黄方平. 液压与气压传动[M]. 第2版. 武汉:华中科技大学出版社, 2016.
LI Bing, HUANG Fangping. Hydraulic and Pneumatic[M]. 2nd ed. Wuhan:Huazhong University of Science and Technology Press, 2016.
[20] 劉献栋, 邓志党, 高峰. 基于逆变换的路面不平度仿真研究[J]. 中国公路学报, 2005(1):126-130.
LIU Xiandong, DENG Zhidang, GAO Feng. Study of Simulation of Road Roughness Based on Inverse Transform[J]. China Journal of Highway and Transport, 2005(1):126-130.
[21] 鲍家定, 伍建伟, 王瀚超, 等. 基于IFFT法的路面不平度时域模拟方法[J]. 现代电子技术, 2016, 39(20):8-11.
BAO Jiading, WU Jianwei, WANG Hanchao, et al. Method for IFFT-based Time-domain Simulation of Road Roughness[J]. Modern Electronics Technique, 2016, 39(20):8-11.
[22] RAJESH R. Vehicle Dynamics and Control[M]. Boston, MA:Springer, 2014.
[23] 余志生. 汽车理论[M]. 第6版. 北京:机械工业出版社, 2018.
YU Zhisheng. Automobile Theory[M]. 6th ed. Beijing:China Machine Press, 2018.
[24] 南京汽车研究所, 郑州机械研究所. GB /T 7031—2005机械振动——道路路面谱测量数据报告[S]. 北京:中国标准出版社, 2005.
Nanjing Automotive Research Institute, Zhengzhou Machinery Research Institute. GB /T 7031—2005 Mechanical Vibration—Road Surface Spectrum Measurement Data Report[S]. Beijing:Standards Press of China, 2005.
[25] 趙济海. 路面不平度的测量分析与应用[M]. 北京:北京理工大学出版社, 2000.
Zhao Jihai. Measurement Analysis and Application of Road Roughness[M]. Beijing:Beijing Institute of Technology Press, 2000.
[26] 米承继, 谷正气, 伍文广, 等. 随机载荷下矿用自卸车后桥壳疲劳寿命分析[J]. 机械工程学报, 2012, 48(12):103-109.
MI Chengji, GU Zhengqi, WU Wenguang, et al. Fatigue Life Analysis of Rear Axle Housing of Mining Dump Truck under Random Load[J]. Journal of Mechanical Engineering, 2012, 48(12):103-109.
[27] 卢剑伟, 王馨梓, 吴唯唯. 路面随机激励下轻型货车驱动桥壳疲劳可靠性分析[J]. 汽车工程, 2016, 38(1):122-126.
LU Jianwei, WANG Xinzi, WU Weiwei. Fatigue Reliability Analysis on the Driving Axle Housing of a Light Truck under Random Road Excitation[J]. Automotive Engineering, 2016, 38(1):122-126.
[28] 杨建国. 小波分析及其工程应用[M]. 北京:机械工业出版社, 2005.
YANG Jianguo. Wavelet Analysis and Its Engineering Applications[M]. Beijing:China Machine Press, 2005.
[29] 刘习军, 相林杰, 张素侠. 基于小波分析的简支梁桥损伤识别[J]. 振动·测试与诊断, 2015, 35(5):866-872.
LIU Xijun, XIANG Linjie, ZHANG Suxia. Damage Identification of Simply Supported Beam Bridges Based on Wavelet Analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5):866-872.
[30] 徐中明, 邱兆强, 余烽, 等. 全地形车车架固有特性分析与改型设计优选[J]. 机械科学与技术, 2011, 30(10):1613-1617.
XU Zhongming, QIU Zhaoqiang, YU Feng, et al. The Analysis and Optimization of Natural Characteristics for the Frame of ATV[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10):1613-1617.
[31] 许国根, 赵后随, 黄智勇. 最优化方法及其MATLAB实现[M]. 北京:北京航空航天大学出版社, 2018.
XU Guogen, ZHAO Housui, HUANG Zhiyong. Optimization Method and MATLAB Implementation[M]. Beijing:Beihang University Press, 2018.
[32] 谭启迪, 薄景山, 常晁瑜, 等. 基于模拟退火算法的设计反应谱标定方法[J]. 地震工程与工程振动. 2020, 40(1):155-161.
TAN Qidi, BO Jingshan, CHANC Chaoyu, et al. Calibrating Method of Seismic Design Response Spectrum Based on Simulated Annealing Algorithm[J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(1):155-161.

