接触式机械密封外圆周织构强化换热机理研究

余旻丰 彭旭东 孟祥铠 梁杨杨

摘要：冲洗是强化机械密封换热的主要措施之一，但在一些特殊场合下冲洗量的大小往往是给定的，因此，需要采取一些强制换热措施来改善机械密封的运行环境。通过在密封环的外周面开设织构，针对冲洗量一定的情况，基于SST k-ω湍流模型，采用Ω方法分析了不同转速下织构深径比对端面温度、外周面局部努塞尔数Nu和织构区域流场的影响，对比研究了动环织构和静环织构的换热机理。研究结果表明：在相同工况、冲洗量和织构几何参数条件下，若动静环外周面单独开设织构，则动环的换热效果更佳。在相同转速下，动环外周面开设织构时，减小深径比会使织构内部换热效果差的区域增大，换热效果减弱，但对于静环织构，减小深径比会使织构流体流动下游侧换热效果差的区域减小，换热效果增强；随着转速的增大，较小深径比动环织构内部出现了新的差换热效果區域，单位面积换热强度显著下降。因此，为获取较优的换热效果，在低转速下宜选取小深径比织构，而在高转速下应选取大深径比织构。

关键词：表面织构; 外周面; 接触式机械密封; 强化换热

中图分类号：TH117.1

DOI：10.3969/j.issn.1004132X.2023.11.002

Research on Heat Transfer Enhancement Mechanism of Contact Mechanical

Seals with Textured Circumference Surfaces

YU Minfeng PENG Xudong MENG Xiangkai LIANG Yangyang

School of Mechanical Engineering，Zhejiang University of Technology，Hangzhou，310014

Abstract： Flushing was one of the main measures for heat transfer enhancement of mechanical seals. But in some special occasions， the flow rate of flushing was given， so some forced heat transfer measures were needed to improve the operating environment of mechanical seals. Through processing texture on the circumference surfaces of the sealing rings and aiming at the condition of a given amount of flushing， the influences of speed and depth to diameter ratio on interface temperature， local Nu on circumference surfaces and flow field in textured regions were analyzed by SST k-ω turbulence model and Ω method， heat transfer mechanism of texture processed on rotor or stator was compared and analyzed. The results show that under the same working conditions， flow rate of flushing and texture geometric parameters， the heat transfer of rotor is better if the texture is set on the circumference surfaces of rotor and stator separately. Under the same speed， when texture is processed on the circumference surface of rotor， reduction of the aspect ratio may increase the areas with poor heat transfer inside the texture and weakened heat transfer. But when texture is processed on the circumference surfaces of stator， the conclusion is completely opposite. As the speed increases， a new area of poor heat transfer appears in a small aspect ratio rotor texture， the heat transfer intensity per unit area is decreased significantly. Therefore， in order to obtain better heat transfer effectiveness， the small aspect ratio texture may be selected under low speed， and the large aspect ratio texture may be selected under high speed.

Key words： texture； circumference surface； contact mechanical seal； heat transfer enhancement

0 引言

机械密封是旋转机器设备的重要零部件，广泛应用于泵、压缩机、釜等设备的轴端密封［1-3］。通常，要求机械密封运行时端面间处于合适的流体润滑状态，以确保泄漏量小甚至零泄漏且端面磨损低，但是，在很多情况下，机械密封泄漏超标的前期预兆或原因并非表现为端面磨损，而是端面过热或温升过高或摩擦扭矩过大，特别是针对航天涡轮泵等设备用机械密封其冲洗量无法调节的特殊使用场合，后一种原因更为常见［4-8］。因此，如何在冲洗量给定的情况下，提高机械密封的传热特别是换热效果，改善机械密封的运行环境已成为航天涡轮泵的难点问题。近期，密封环外周面开设织构的方法由于兼顾了较好的强化换热效果和较小的搅拌损失而受到关注［9-11］。

关于织构表面换热机制的研究最初是以平板表面为研究对象。AFANASYEV等［12］在平板表面设置了半球形织构，实验测量了不同深度、不同半径、不同排布织构内部的温度分布和速度分布，确定了半球形织构的强化换热效果，这一结果被LIN等［13］通过数值模拟得到了验证。CHYU等［14］同样采用平板表面进行实验，通过测量半球形和水滴形织构的内部温度分布，发现尽管二者的局部温度分布存在微小差异，但计算所得整体努塞尔数Nu基本相等。

MAHMOOD等［15］使用两块相隔一定间距的矩形平板组成的狭窄通道来模拟微通道换热器，并在通道内壁面加工交错分布的规则半球形织构，综合采用粒子图像测速（particle image velocimetry， PIV） 技术和壁面测温技术，获得了半球形织构内部流场和局部努塞尔数，分析了Re=600～11 000时量纲一高度H/D（其中H为平板间距，D为半球形织构直径）、入口温度对通道内壁面半球形织构换热效果的影响［16］，研究结果表明，随着H/D的减小和入口温度的降低，织构的换热效果增强。

在上述基础上，多位学者［17-20］分别对圆柱形织构、倾斜侧壁织构、六边形织构和椭圆形织构进行研究，对比了这些织构与半球形织构的换热效果。LIGRANI等［21］在通道的上下壁面设置对称的凸起与织构，考虑错位因素的影响，对流场、局部努塞尔数和流动摩阻进行了测试，结果表明凸起表面强化换热的效果更佳，但阻力增大了2～2.7倍。LIU等［22］在半球形织构通道的内壁面加入半球形凸起，并考虑了凸起和织构的几何和排布参数对换热效果的影响，同样发现凸起能有效提高下游织构的强化换热效果，但流动阻力也相应增大了。XIE等［23］将方形直通道改为方形U形通道，以模拟叶片尖端流道，并在通道内壁半球形织构之间加工了圆柱形凸起，研究结果表明，不同部位的局部努塞尔数提高了3.2%～31.5%，流动阻力同时也增大了2.3% ～16.2%。

NIAN等［9］率先提出在机械密封外圆周表面加工织构并进行了相关的实验，结果证实这一技术在中低转速和中低压情况下能降低端面温度10%左右；随后他们又研究了中低速条件下外圆周圆柱形织构的排布和几何参数对换热强化的影响［10］，发现小尺寸、高密度的织构换热效果更佳。周宇坤等［11］针对多种织构的换热效果开展了初步研究，结果表明旋转角为90°的等边三角形织构具有最佳强化换热效果，矩形织构强化换热效果最差。

为了更高效地对流场进行量化分析，研究者们采用了Ω涡识别方法。截至目前，对涡的分析方法已经历了三代［24-25］：①基于涡量的涡识别方法，即直接使用涡量定义法识别涡，认为涡量的大小即为当地旋转运动的强度，但已经被证明存在大误差，且高涡量区域和实际的涡结构关联性很低；②第二代涡识别方法，其基本方法是设置一个判定参数和一个阈值，当计算出的判定参数数值大于阈值时，认为当地有涡，但阈值的选择将极大程度地影响识别结果且判定参数物理意义不明；③第三代涡识别方法，包括Ω涡识别方法和Liutex向量法，其优点是将参数的阈值归一化至0.52，使涡中心位置和强度的判定更为精准。

上述工作表明，在众多换热手段中，织构能兼顾强换热效果和低摩阻损失，同时无需占用额外空间，在空间受限的航天涡轮泵密封腔体内是一种理想的强化换热措施。但是，截止目前，绝大多数研究还是以无限大平板和微通道换热器为研究对象，这与传统密封腔内部的流动与传热的情况存在明显不同。此外，织构应用于机械密封的研究多以端面开设织构为主［26-28］，而在冲洗量给定的条件下，高速机械密封外圆周面织构的换热机理鲜有研究。因此，本文采用SST湍流模型对比分析了密封动环或静环外周面织构的内部流场和局部努塞尔数，使用Ω方法对密封腔内部和织构局部的漩涡进行了识别，讨论了不同深径比外周面织构动环和静环的换热效果及其变化，研究了转速对动环织构换热效果的影响，揭示了织构的换热机理。

1 数值模型

1.1 几何模型

图1为一种典型的高速涡轮泵用机械密封的结构示意图，其中，机械密封动环或静环的外周面加工有织构。为提高计算效率，考虑到动环和静环沿圆周方向的对称性，截取环整体的1/18作为计算域，建立包含动环、静环、密封腔内流体的计算模型，相关几何参数如图1、图2和表1所示。

1.2 流动传热控制方程

本文重点分析研究在不同织构深径比和转速条件下机械密封端面温度变化及密封腔和织构内部的流动状态。为便于分析，可作如下假设：流体在接触面上无滑移；忽略密封端面的表面粗糙度与波度、密封环的热力变形和端面泄漏；不考虑介质物性变化及热辐射；由于接触式机械密封泄漏量极小，故忽略端面处介质泄漏对温度场的影响。考虑到密封环在腔体内旋转，腔内流体容易处于湍流状态，本文采用商业软件ANSYS FLUENT 2020R2内的SST k-ω湍流模型（下文简称SST模型）来计算腔内流体的压力场、速度场，并结合能量方程来模拟计算传热及温度场。已有的研究［9，11］使用了RNG k-ε湍流模型配合壁面函数作为流动传热控制方程，但这种研究方法对壁面量綱一参数y+的依赖性较大［29-31］。其中，量纲一参数y+的定义以及RNG k-ε模型中y+应满足的取值范围如下［31］：

式中，cμ为经验常数，取cμ=0.09；k为湍动能；ν为流体运动黏度；y为流体域内第一个节点与固体壁面间的距离。

本文涉及织构内部速度场分析，若使用RNG k-ε模型配合壁面函数方法，则由于第一层网格不能过密，织构内小漩涡将会难以分辨，而SST模型通过混合函数F的不同取值，分别在近壁面区域和湍流旺盛区域使用k-ω模型和k-ε模型，这样就能同时确保壁面换热和织构内部流动的计算精度，因此，本文使用SST模型，该模型y+仅需要满足近壁区湍流模型（即k-ω模型）的要求，确保y+≤1即可［32-34］。

FLUENT中SST k-ω模型的稳态不可压缩流表达式如下：

式中，ρ为介质密度；k为湍动能；ω为湍流耗散率；Γk、Γω分别为k和ω的有效扩散项；Gk、Gω分别为k和ω的方程；Yk、Yω分别为k和ω的发散项；Dω为正交发散项；Sk、Sω为用户自定义源项；xi、xj为各坐标方向的张量表示，下标i、j为哑标；ui为液相速度矢量的分量。

式（2）和式（3）中各项除Sk与Sω以外均由FLUENT默认给出，本文不使用源项。其他计算中所涉及的模型常数的取值见表2，其中φ1、φ2为参数φ在计算过程中使用的中间值，φ=φ1F+φ2 （1-F），F为混合函数，F在近壁区取1，在湍流旺盛区取0；α为边界层内部剪切应力与湍动能之比；β为k方程的耗散项经验常数;σk、σω分别为k方程和ω方程中的扩散项经验常数。

1.3 涡分析方法

Ω方法定义了一个Ω：

其中，e是一个任意取值很小的正数，A是涡量中非旋转（变形）的部分，B是涡量中旋转部分，V表示对速度矢量进行三维哈密顿运算。这一方法推荐选取Ω≥0.52的等值面来展示涡，这一推荐阈值意味着涡量的旋转部分超过了变形耗散部分，且这一数值适用于大多数经验案例［24-25］。本文使用Tecplot的自定义方程计算密封腔内各部位流场的Ω，并对内部涡分布进行了分析。

图3为主轴转速为5400 r/min时，分别使用Ω方法和涡量分析法获得的密封腔内部轴对称平面上的漩涡强度云图，Ω和涡量的数值越大表明漩涡强度越高。可以看出，由于动环的旋转，动环外圆周近壁区的速度梯度远大于其余区域的速度梯度，因此采用涡量分析法得到在动环外圆周近壁区出现了更大的涡量数值，而Ω方法则识别出了密封腔内部存在两

个旋转方向相反的主要漩涡（下文简称主涡）。对于图1所示的几何结构，密封腔可以近似视为一种内壁面旋转的有限长同心圆环腔体内部的泰勒库艾特流［35］，显而易见，Ω方法识别出的主涡形态符合泰勒涡的形态，而涡量分析法则完全无法识别，因此，Ω方法相比于涡量分析法更适合本文设计研究对象的流动传热分析。

1.4 边界条件

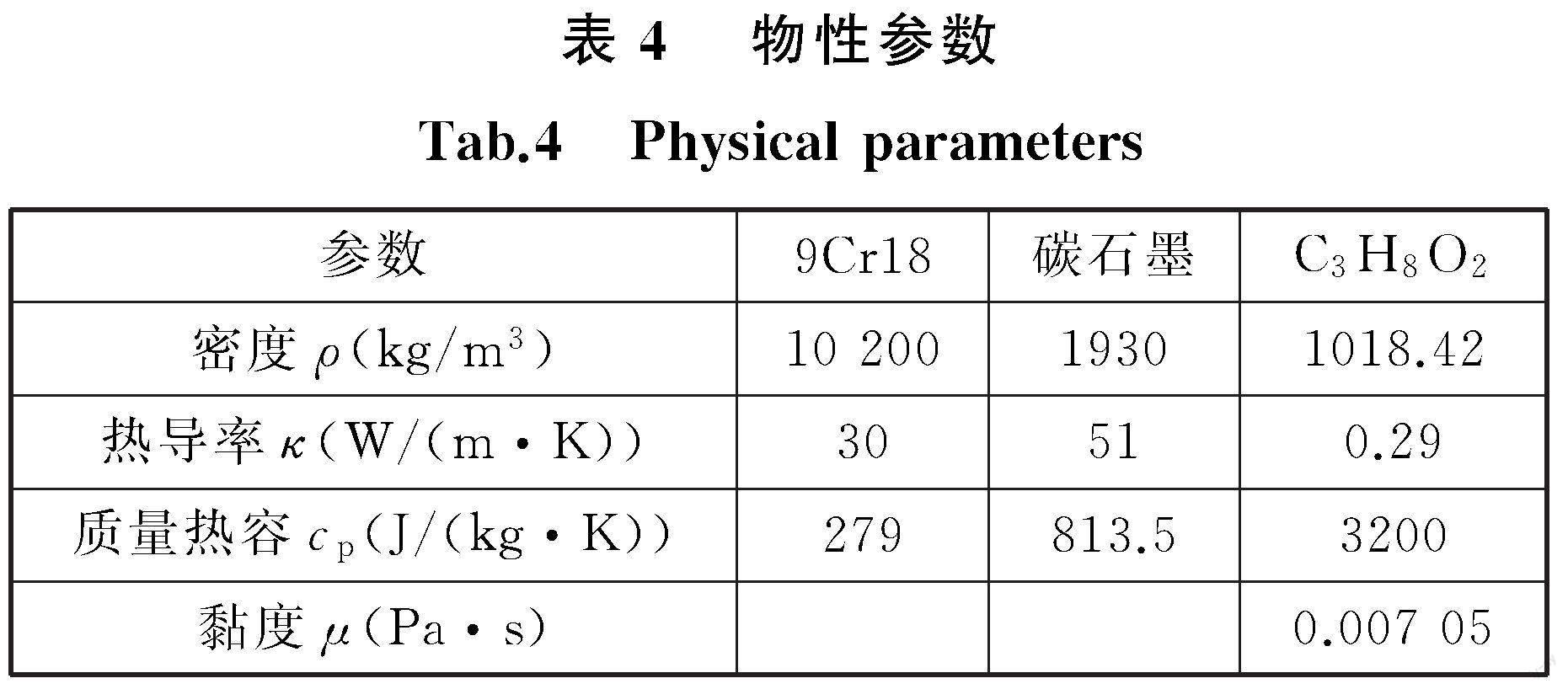
根据实际使用中高速涡轮泵机械密封的安装特点，由图1可知，密封腔内流体的入口设置于动环背部，出口设置于静环外侧。常用冲洗流量一般为8～25 L/min，这里为安全起见，选取下限值8 L/min作为冲洗流量的计算用值，因此计算得到入口流速约为0.1 m/s。端面的摩擦热参考NIAN等［9］提出的方法进行计算并加载于图2所示的WR和WS面上，本文所使用摩擦热公式中的关键参数为端面摩擦因数f，由摩擦状态决定，软硬配对的接触式机械密封启动时端面摩擦因数较大，稳定运行后端面摩擦因数将会减小，一般取值范围在0.1～0.2之间，极少数能达到0.25［36］，这一范围适用于混合摩擦、边界摩擦及干摩擦，又考虑到高转速会导致摩擦因数增大，本文选取f=0.15，这既不影响中低转速时的产热计算，也考虑了高转速对端面产热模型的影响。本研究认为动、静环内径处与大气之间存在热对流，根据经验公式［37］可计算出对流传热系数分别为72 W/（m2·K）和0.1 W/（m2·K），最后，设置WR与WS为耦合壁面， 这样FLUENT就会根据产热量、温度场及材料物性自动将端面摩擦热分配至动环与静环。具体边界条件列于表3，表中T为壁面温度，v为入口流速，p为出口压力，q为壁面热通量，h为对流传热系数，n为主轴转速。各边界编号见图2，密封环材料和密封介质的物性参数如表4所示。

1.5 参数定义

1.6 网格无关性与模型正确性验证

采用ICEM软件对所截取密封环和腔内流体进行网格划分，环与流体均采用完全六面体网格划分，对网格进行规则加密。图4a为网格局部加密总示意图，图4b为动、静环外周加密示意图，图4c为端面加密示意图，图4d为织构底面加密示意图，图4e为织构侧壁面加密示意图，局部加密规则为：①确保壁面y+≤1；②边界层至少铺15层网格；③边界层内部网格尺寸增长倍率为1.2～1.4，以接近1.2为宜。

网格无关性验证和模型正确性验证如图5所示，其中Z为本研究模型中密封环轴向坐标，z为文献［41］所给的密封环轴向坐标，零值为端面所在平面处轴向坐标。图5a所示为网格无关性验证结果，选取网格数N分别为5×105、1×106、2×106的网格进行网格无关性验证，以端面径向温度分布为衡量标准。

如图5a所示，当网格数增加至1×106时，再增大一倍网格尺寸，端面温度曲线各点数值变化小于0.5 ℃，相对误差在0.7%以内，综合考虑计算时间和计算精度，选取1×106数量网格作为计算网格。图5b所示为模型正确性验证，可以看出，在对比文献［41］所给参数条件下，使用本文模型计算所得的三个不同轴向位置的径向温度分布与对比文献实验值的变化规律均吻合较好，各点温度偏差均小于0.5 ℃，相对误差均在1.5%以内，优于对比文献的数值模拟结果。究其原因，本文主要改进了所使用的湍流模型，RNG k-ε湍流模型要求壁面y+较大，而SST模型仅需加密边界层确保y+≤1即可较好地符合实驗数据，在流动结构简单时，RNG k-ε湍流模型能有效减少计算所需资源，但本文涉及跨尺度流动问题，使用SST模型效果更佳。

2 结果分析

2.1 动、静环织构作用效果规律

图6为不同深径比情况下动、静环织构对端面最高温度的降低幅度曲线图。图6a与图6b表明，与静环织构相比，动环织构强化换热效果远胜，降温幅度Δt平均高出5倍左右。除此之外，对不同深径比γ下的动、静环织构进行分析发现，Δt随γ的变化曲线存在转折点。动环曲线的转折点在γ=0.13附近，γ≥0.13时，改变γ会对Δt产生显著影响，γ减小0.09，Δt增大了100%（5 ℃）；γ<0.13时，改变γ对Δt的影响较小，γ减小0.05，Δt仅增大了10%（1 ℃）。静环也存在γ-Δt曲线突变点（对应γ=0.1），但与动环不同，当γ>0.1时，织构换热效果变化不显著，γ减小0.3，Δt可以认为不变（增大了0.7 ℃，33%）；当γ<0.1时，γ减小0.02，Δt就已经达到了之前的总和（0.7 ℃），但总体而言，静环织构的换热效果差，降温幅度小，不推荐在此工况下使用。由于动环换热效果远胜于静环换热效果，进一步扩大转速范围，讨论转速n为1800～12 600 r/min工况下不同深径比动环织构的降温幅度变化规律，如图6c所示。五种织构的Δt/tnmax均随转速提高而减小，但大深径比织构在经历初期的骤降之后，在中高转速下Δt/tnmax的减小几乎可以忽略不计，而小深径比织构Δt/tnmax近似呈直线下降。

2.2 动、静环织构强化换热机理差异性分析

图7为密封腔内部轴对称平面的漩涡强度云图，图7a所示为主轴转速n=1800 r/min时的内部漩涡强度，图7b所示为主轴转速n=12 600 r/min时的内部漩涡强度，主涡集中于动环和静环外部，近似于泰勒库艾特流［35］。两个主涡的产生机理各不相同，靠近轴末压盖（图7中Z轴正方向末端）的漩涡（涡1）是由压力出口的回流撞击轴末压盖和静环外周形成的。动环外侧漩涡（涡2）的形成原因则较为复杂，涡1压迫了入口流体的流动范围，迫使入口流体仅能从涡1的右侧穿过，如此形成Y轴正向速度，但出口流道由于回流占据了部分范圍而变得较为狭窄，因此部分流体将会沿Z轴负向回流并撞击顶部壁面，又因为入口流的进入，涡2的Z向范围也受到了限制。在不同转速下均观察到了这一现象，但当转速提高时，涡心的漩涡强度增大，从0.8 （n=1800 r/min）增大至0.95 （n=12 600 r/min）；对设置织构的机械密封进行同样的分析可知，两个主涡的强度和位置几乎不受织构的影响。

进行换热机理差异性分析时需要对织构内和织构周边的换热效率分布和速度场等进行分析，由于本文织构深度较浅（0.2 mm），侧壁面面积过小，换热能力可以忽略不计，因此本文将主要针对织构底面和织构周边的外周壁面的换热效果进行研究。选取γ=0.13作为分析对象，图8为n=1800 r/min、γ=0.13时静环和动环外周面换热效率分布云图，其中ηj0、ηd0 分别为n=1800 r/min时的静环外周面换热效率和动环外周面换热效率。织构上游和织构下游以圆心为界，主流进入侧为织构上游，主流离开侧为织构下游，织构上游和织构下游包括织构外部附近的外圆周壁面，特别定义织构下游较长的显著影响区为尾迹区。

在上文分析的基础上，选取了图9所示的切片位置作进一步分析。图9a所示为仅在动环设置织构时的切片位置，图9b所示为仅在静环设置织构时的切片位置。无论密封环外周面是否设置织构，在图1和图2所示的几何及边界条件下均具有周向轴对称性，因此，选取中轴面即X=0截面进行切片；Z=-1.5 mm和Z=4 mm位置分别为动环织构和静环织构最佳换热效果的中心平面；图9中①和②的虚线圆所示范围是综合了周向轴对称性和外周面换热效果选取的位置。

图10为Z=-1.5 mm横截面流线图，其中vm为流体流速，通过三维速度矢量求模获得。与半球形织构类似［39-41］，圆柱形织构也可分为流动分离区、流动循环区、冲击区和流动重附着区。入口侧的流动分离区与半球形织构类似，出现在几何突变点附近，此区域换热效率低，换热效率值接近于1；流动循环区在动环中表现为规则漩涡，在静环中表现为杂乱流动，但总体均沿几何结构向下游流动，且此部分流体与织构底面不发生接触，对织构底面换热效率无增强作用；冲击区成因与半球形织构不同，是织构入口位置循环区之外的流体在进入织构后形成垂直流动并冲击织构底面形成的，这一流动破坏了原本近壁面区域的热边界层，使织构入口附近的换热效率值接近于10；动环织构内大部区域的流体流动均以近似层流形式进行，相应热边界层厚度也开始增大，使动环织构底面换热效率值规则地减小；最后，流体在出口附近出现了二次流动分离和离开织构后的流动再附着，二次流动分离产生了图8中尾迹区中间的低换热区域，而流动再附着形成了高换热长尾迹区。

图11为Z=4 mm横截面流线图，静环织构内部流体流动速度极低，同时内部流动状态也与动环织构内有较大的不同。入口分离区仍然位于几何突变区附近，但循环区范围增大，且深度范围扩大至接近h0，同时在下游位置出现了二次的循环区，2个循环区不仅压缩了冲击区范围，还增大了局部热边界层厚度，因此静环内部换热效率值极小。最后一个区域是下游附近的流动再附着区，这一区域从下游循环区的上部开始，一直延续至下游较远的位置，对应于图8中静环织构下游ηj0>1.5的区域。

图12为织构内部三维流线图，为了能更直观地显示流线全貌，对固体壁面进行了透明处理。图12b表明静环织构内部流体进入织构后会分为两股，分别以红、蓝流线表示，红色流线沿逆时针方向流动后紧贴壁面流出，蓝色流线在织构内部形成较大范围的再循环流动，随后顺时针流出，蓝色流线部分的流体在流出织构时出现了与动环相同的喷射流，这是图8中静环织构下游仅有一块再附着区且高换热区范围小的主要原因。图12a中动环织构入口流分为了两层，下层贴壁流体以红色流线表示，这部分流体产生了图10中的入口流动分离区、循环区和部分冲击区，随后流体沿着侧壁以漩涡的形式向两侧流动，离开织构后在外部形成两块再附着区并进入下一织构，是织构下游长条状尾迹区的成因；上层流体以蓝色流线表示，这部分流体进入后，形成了图10中部分冲击区和下游附近的近似层流区，最后在下游织构侧壁产生分离区和喷射流，分离区和喷射流导致尾迹区中间出现低换热区域。

2.3 深径比对动、静环织构强化换热的影响分析

2.1节已经说明，深径比对织构强化换热机理存在影响，本节将截取图9中①和②虚线圆周边区域，进一步分别分析动、静环织构γ发生变化时换热效果的变化规律。图13为各深径比动环外圆周换热效率分布云图，可以看出，当γ减小时，织构底部高换热效果的相对面积开始减小，表明织构的整体换热效率有随γ减小而降低的趋势；当γ<0.13时，织构的尾迹区开始受到下一排织构的几何尺度限制，尾迹区范围减小，尾迹区换热效果变差。这解释了为何织构γ<0.13时，端面最高温度的降温幅度随γ减小而增大的趋势开始急剧减缓。

图14为各深径比静环外圆周换热效率分布云图。与动环相反，当γ减小时，静环织构内部换热效果增强，且在本文研究的深径比范围内，静环织构的主要换热位置都是流体离开织构后形成的尾迹区，改变深径比仅仅改变了尾迹区的范围和角度。

图15为γ=0.08时动环织构内部主流的横截面流线图，可以看出，深径比减小时，主要流场变化不大，入口的循环区和冲击区也仍然存在，这主要是因为深度方向的几何尺寸没有发生变化，导致在入口附近小空间内，深度方向的几何突变几乎没有改变流场，但直径尺寸的大小影响了入口循环流动形成的漩涡尺寸。当深径比过小时，入口处循环流动形成的漩涡将在深度方向增大，使得垂直流减弱，冲击区范围减小，高换热区域缩小；其次，减小的深径比使得织构底面总面积增大，导致高换热区域的相对面积减小，减弱了织构的换热能力。

图16为γ=0.08时静环织构内部主流的横截面流线图。对于静环织构，γ变小后入口位置循环区几乎没有发生变化，但右下角的二次循环区占比显著减小了，这变相增大了冲击区的面积占比。循环区是低换热区，冲击区是高换热区，二者的相对面积变化使得静环换热效率随深径比减小而提高。此外，小γ时静环织构内部流速仍然接近于0，因此虽然静环内部换热效率值有所增大，仍然比动环内部换热效率值小得多。

虽然小深径比动环织构和大深径比动环织构在主流方向横截面的流线相差不大，但上述两种动环织构的内部垂直主流方向流场则出现了较大的不同。图17为不同深径比动环织构X=0截面局部流线图，可以看出，两种情况下织构内部流体均存在左右两侧同时进入织构的情况， γ=0.2时左侧入口流体占据主体，右侧入口流体仅在进入织构后的小范围内生成漩涡；γ=0.08时，左右两侧进入织构的流体在织构中心区产生了碰撞，并且在碰撞界面附近形成了两个强烈的漩涡，这些漩涡外层的流体又在织构底面附近呈现出近似层流的流态，降低了小深径比织构中心及下游位置的换热效率，但对于静环织构，并无这一现象。

2.4 主轴转速对动环织构强化换热的影响分析

选取γ=0.1和γ=0.2分别代表大深径比和小深径比两种情况进行进一步的分析。图18为γ=0.1和γ=0.2时n分别为1800 r/min和12 600 r/min工况下的动环织构换热效率云图，可以看出，在转速提高后，换热效率值减小，验证了前文所获得的规律，即在高速情况下，织构的换热效果变差。此外，转速提高后，尾迹区换热效率值也随之减小。

3 结论

（1）织构强化换热机理是外周面织构的设置促成了垂直于壁面的流动，该流动通过破坏流体绕流的热边界层，增大了局部努塞尔数，增强了换热效果。

（2）静环外周面织构内部及其周边流速均低于动环外周面织构对应区域的流速，热边界层较厚，因此前者换热效果远不如后者。

（3）当深径比减小时，入口处循环涡旋将会增大，入口垂直流受到循环涡旋影响，占据范围减小，使得冲击区范围被压缩，局部努塞尔数减小。

（4）转速增大时，流体在织构内部平行于壁面方向流速的增幅远大于垂直于壁面方向流速的增幅，流体流动方向与壁面间夹角减小，导致织构整体换热效果变差。此外，对于小深径比织构，将会在下游形成新的循环区，使局部努塞尔数急剧减小。

参考文献：

［1］ LUAN Z G， KHONSARI M M. Analysis of Conjugate Heat Transfer and Turbulent Flow in Mechanical Seals［J］. Tribology International， 2009， 42（5）：762-769.

［2］ TAKAMI M R， GERDROODBARY M B， GANJI D D. Thermal Analysis of Mechanical Face Seal Using Analytical Approach［J］. Thermal Science and Engineering Progress， 2018， 5：60-68.

［3］ MOSAVAT M， MORADI M， TAKAMI M R， et al. Heat Transfer Study of Mechanical Face Seal and Fin by Analytical Method［J］. Engineering Science and Technology—an International Journal， 2018， 21（3）：380-388.

［4］ LUAN Z G， KHONSARI M M. Heat Transfer Correlations for Laminar Flows within a Mechanical Seal Chamber［J］. Tribology International， 2009， 42（5）：770-778.

［5］ 顧永泉， 吴宗祥， 王丽娟. 机械密封的端面温度［J］. 流体工程， 1985， 4：3-10.

GU Yongquan， WU Zongxiang， WANG Lijuan. End Face Temperature of Mechanical Seal［J］. Fluid Machinery， 1985， 4：3-10.

［6］ 張淑敏， 胡丽国， 孟祥铠. 超高速燃气涡轮泵机械密封的分析与研究［J］. 流体机械， 2010， 40（10）：23-27.

ZHANG Shumin， HU Liguo， MENG Xiangkai. Analysis of a Mechanical Seal for Superspeed Gas Turbopump［J］. Fluid Machinery， 2010， 40（10）：23-27.

［7］ 彭旭东， 金杰， 李定， 等. 高速涡轮泵机械密封端面温度变化规律研究［J］. 摩擦学学报， 2019， 39（3）：313-318.

PENG Xudong， JIN Jie， LI Ding， et al. Analysis of Face Temperature in Mechanical Seal Applied in the High Speed Turbopump［J］. Tribology， 2019， 39（3）：313-318.

［8］ KENNEDY F E， KARPE S A. Thermocracking of a Mechanical Face Seal［J］. Wear， 1982， 79（1）：21-36.

［9］ NIAN X， KHONSARI M M. Thermal Performance of Mechanical Seals with Textured Side-wall［J］. Tribology International， 2012， 45（1）：1-7.

［10］ NIAN X， KHONSARI M M. Improving Thermal Performance of Mechanical Seals with Surface Texturing［J］. Proceedings of the Institution of Mechanical Engineers，Part J：Journal of Engineering Tribology， 2015， 229：350-361.

［11］ 周宇坤， 彭旭东， 赵文静， 等. 机械密封动环外周表面织构换热机理及结构优化［J］. 摩擦学学报， 2020， 40（4）：538-550.

ZHOU Yukun， PENG Xudong， ZHAO Wenjing， et al. Study on Heat Transfer Mechanism and Optimization of Circumferential Texture of Mechanical Seal［J］. Tribology， 2020， 40（4）：538-550.

［12］ AFANASYEV V N， CHUDNOVSKY Y P， LEONTIEV A I， et al. Turbulent Flow Friction and Heat Transfer Characteristics for Spherical Cavities on a Flat Plate［J］. Experimental Thermal and Fluid Science， 1993， 7（1）：1-8.

［13］ LIN Y L， SHIH T I P， CHYU M K. Computations of Flow and Heat Transfer in a Channel with Rows of Hemispherical Cavities［C］∥Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition. Indianapolis：ASME， 1999：99-GT-263.

［14］ CHYU M K， YU Y， DING H， et al. Concavity Enhanced Heat Transfer in an Internal Cooling Passage［C］∥Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition. Orlando：ASME， 1997：97-GT-437.

［15］ MAHMOOD G I， HILL M L， NELSON D L， et al. Local Heat Transfer and Flow Structure on and above a Dimpled Surface in a Channel［J］. Journal of Turbomachinery， 2001， 123（1）：115-123.

［16］ MAHMOOD G I， LIGRANI P M. Heat Transfer in a Dimpled Channel：Combined Influences of Aspect Ratio， Temperature Ratio， Reynolds Number， and Flow Structure［J］. International Journal of Heat and Mass Transfer， 2002， 45（10）：2011-2020.

［17］ MOON S W， LAU S C. Turbulent Heat Transfer Measurements on a Wall with Concave and Cylindrical Dimples in a Square Channel［C］∥Proceedings of the ASME Turbo Expo 2002：Power for Land， Sea， and Air. Amsterdam：ASME， 2002：459-467.

［18］ DYACHENKO A Y， TEREKHOV V I， YARYGINA N I. Turbulent Flow Past a Transverse Cavity with Inclined Side Walls［J］. Journal of Applied Mechanics and Technical Physics， 2007， 48：486-491.

［19］ BUTT U， EGBERS C. Flow Structure due to Hexagonal Cavities and Bumps on a Plate Surface［J］. Thermophysics and Aeromechanics， 2016， 23：839-847.

［20］ TURNOW J， KORNEV N， ISAEV S， et al. Vortex Mechanism of Heat Transfer Enhancement in a Channel with Spherical and Oval Dimples［J］. Heat Mass Transfer， 2011， 47：301-313.

［21］ LIGRANI P M， MAHMOOD G I， HARRISON J L， et al. Flow Structure and Local Nusselt Number Variations in a Channel with Dimples and Protrusions on Opposite Walls［J］. International Journal of Heat and Mass Transfer， 2001， 44（23）：4413-4425.

［22］ LIU Jian， SONG Yidan. Numerical Modeling Flow and Heat Transfer in Dimpled Cooling Channels with Secondary Hemispherical Protrusions［J］. Energy， 2015， 79：1-19.

［23］ XIE Yonghui， SHI Dongbo， SHEN Zhongyang. Experimental and Numerical Investigation of Heat Transfer and Friction Performance for Turbine Blade Tip Cap with Combined Pin-Fin-Dimple/Protrusion Structure［J］. International Journal of Heat and Mass Transfer， 2017， 104：1120-1134.

［24］ LIU Chaoqun， WANG Yiqian， YANG Yong， et al. New Omega Vortex Identification Method［J］. Physics， Mechanics & Astronomy， 2016， 59（8）：684711.

［25］ YU Y F， SHRESTHA P， ALVAREZ O， et al. Investigation of Correlation between Vorticity， Q， λci， λ2， Δ and Liutex［J］. Computers & Fluids， 2021， 225：104977.

［26］ 陳文杰， 孟祥铠， 王玉明， 等. 机械密封织构化表面粗糙度效应的有限元模型与摩擦学特性分析［J］. 摩擦学学报， 2019， 39（5）：523-530.

CHENG Wenjie， MENG Xiangkai， WANG Yu-ming， et al. Finite Element Model and Tribological Properties Analysis of Textured Mechanical Seals Considering Roughness Effect［J］. Tribology， 2019， 39（5）：523-530.

［27］ 程健梁. 机械密封复合织构化端面密封性能与形貌演化［D］. 杭州：浙江工业大学， 2020.

CHENG Jianliang. Sealing Performance and Morphology Evolution of Composite Textured End Face of Mechanical Seal［D］. Hangzhou：Zhejiang University of Technology， 2020.

［28］ ADJEMOUT M， BRUNETIRE N， BOUYER J. Numerical Analysis of the Texture Effect on the Hydrodynamic Performance of a Mechanical Seal［J］. Surface Topography：Metrology and Properties， 2016， 4（1）：014002.

［29］ TEKRIWAL P. Heat Transfer Predictions with Extended k-ε Turbulence Model in Radial Cooling Ducts Rotating in Orthogonal Mode［J］. Journal of Heat Transfer， 1994， 116：369-380.

［30］ WANG L B，WANG Q W， HE Y L， et al. Experimental and Numerical Study of Developing Turbulent Flow and Heat Transfer in Convergent/Divergent Square Ducts［J］. Heat and Mass Transfer， 38：399-408.

［31］ 陶文铨. 数值传热学［M］. 2版.西安：西安交通大学出版社， 2001：353-362.

TAO Wenquan. Numerical Heat Transfer［M］. 2nd ed. Xian：Xian Jiaotong University Press， 2001：353-362.

［32］ MENTER F R. Review of the Shear-stress Transport Turbulence Model Experience from an Industrial Perspective［J］. International Journal of Computational Fluid Dynamic， 2009， 23（4）：305-316.

［33］ 王震. 基于钝体风压数据驱动的SST k-ω湍流模型参数修正［D］. 哈尔滨：哈尔滨工业大学， 2020.

WANG Zhen. Parameter Modification of SST k-ω Turbulence Model Based on Bluff Body Wind Pressure Data［D］. Harbin：Harbin Institute of Technology， 2020.

［34］ STEPHEN K R. Coherent Motions in the Turbulent Boundary Layer［J］. Annual Review of Fluid Mechanics， 1991， 23：601-639.

［35］ 丁仕成. 沟槽结构参数对湍流Taylor-Couette流动及其换热特性影响的研究［D］. 镇江：江苏大学， 2018.

DING Shicheng. Research of Slit Structure Parameters Effect on the Turbulent Taylor-Couette Vortex Flow and Heat Transfer Characteristics［D］. Zhenjiang：Jiangsu University， 2018.

［36］ 顾永泉. 机械密封实用技术［M］. 北京：机械工业出版社， 2001：89-90.

GU Yongquan. Practical Technology of Mechanical Seal［M］. Beijing：Machinery Industry Press， 2001：89-90.

［37］ 彭旭东， 谢友柏， 顾永泉. 机械密封端面温度的确定［J］. 化工机械， 1996， 23（6）：333-366.

PENG Xudong， XIE Youbai， GU Yongquan. Determination of the End Face Temperature of Mechanical Seal［J］. Chemical Engineering & Machinery， 1996， 23（6）：333-366.

［38］ GRIFFITH T S， AL-HADHRAMI L， HAN J. Heat Transfer in Rotating Rectangular Cooling Channels （AR=4） with Dimples［J］. Journal of Turbomachinery， 2003， 125（3）：555-563.

［39］ NOURIN F N， BLUM B L， AMANO R S. Evaluation of Heat Transfer Enhancement on Rotational Gas Turbine Blade Internal Cooling Channel with Dimpled Surface［J］. Journal of Energy Resources Technology， 2022， 144（11）：112105.

［40］ NOURIN F N， AMANO R S. Experimental Study on Flow Behavior and Heat Transfer Enhancement with Distinct Dimpled Gas Turbine Blade Internal Cooling Channel［J］. Journal of Energy Resources Technology， 2022， 144（7）：072101.

［41］ PARVIZ M， NORI A O， ROBERT L P， et al. Experimental and Computational Investigation of Flow and Thermal Behavior of a Mechanical Seal［J］. Tribology Transactions， 1999， 42（4）：731-738.

［42］ 張冠敏. 复合波纹板式换热器强化传热机理及传热特性研究［D］. 济南：山东大学， 2006.

ZHANG Guanmin. Research on Heat Transfer Enhancement Mechanism and Heat Transfer Characteristic of Compound Corrugation Plate Heat Exchanger［D］. Jinan：Shandong University， 2006.